Применение закона Ома на практике
Принцип работы одного из основополагающих законов электротехники хочется начать объяснять с аллегории — показа небольшого карикатурного изображения 1 из трех человечков под именами «Напряжение U», «Сопротивление R» и «Ток I».
На нем видно, что «Ток» пытается пролезть через сужение в трубе, которое «Сопротивление» усердно затягивает. В то же время «Напряжение» прилагает максимально возможное усилие для прохождения, проталкивания «Тока».
Этот рисунок напоминает, что электрический ток — это упорядоченное движение заряженных частиц в определенной среде. Передвижение их возможно под действием приложенной внешней энергии, создающей разность потенциалов — напряжение. Однако, внутренние силы проводников и элементов схемы уменьшают величину тока, оказывают сопротивление его перемещению.
Рассмотрим простую схему 2, поясняющую действие закона Ома для участка электрической цепи постоянного тока.
В качестве источника напряжения U используем аккумуляторную батарею, которую подключим к сопротивлению R толстыми и одновременно короткими проводами в точках А и В. Допустим, что провода не влияют на величину прохождения тока I к резистору R.
Формула (1) выражает соотношения между сопротивлением (омы), напряжением (вольты) и током (амперы). Ее называют законом Ома для участка цепи. Кружок под формулой облегчает ее запоминание и пользование для выражения каждого из составляющих параметров U, R или I (U расположено сверху над черточкой, а R и I — снизу).
Если надо определить один из них, то мысленно закрываем его и работаем с двумя оставшимися, выполняя арифметические действия. Когда величины расположены на одной строчке, то их перемножаем. А в случае расположения их на разных уровнях выполняем деление верхнего на нижний.
Эти соотношения показаны на формулах 2 и 3 рисунка 3 ниже.
В этой схеме для измерения тока используется амперметр, который соединен последовательно с нагрузкой R, а напряжения — вольтметр, подключенный параллельно точкам 1 и 2 резистора. Учитывая конструктивные особенности приборов, допустим, что амперметр не влияет на величину тока в схеме, а вольтметр — напряжения.
Определение сопротивления с помощью закона Ома
Пользуясь показаниями приборов (U=12 В, I=2,5 А) можно по формуле 1 определить величину сопротивления R=12/2,5=4,8 Ом.
На практике этот принцип заложен в работу измерительных приборов — омметров, определяющих активное сопротивление различных электрических устройств. Поскольку они могут быть настроены на замеры различных диапазонов величин, то их соответственно подразделяют на микроомметры и миллиомметры, работающие с малыми сопротивлениями и тера-, гиго- и мегаомметры — измеряющие очень большие значения.
Для конкретных условий эксплуатации их выпускают:
-
переносными;
-
щитовыми;
-
лабораторными моделями.

-
Принцип работы омметра
Для выполнения замеров обычно используются магнитоэлектрические приборы, хотя в последнее время широко внедряются электронные (как аналоговые, так и цифровые).
В омметре магнитоэлектрической системы используется токоограничивающий резистор R, пропускающий через себя только миллиамперы и чувствительная измерительная головка (миллиамперметр). Она реагирует на протекание малых токов через прибор за счет взаимодействия двух электромагнитных полей от постоянного магнита N-S и поля, создаваемого током, проходящим через обмотку катушки 1 с токопроводящей пружинкой 2.
В результате взаимодействия сил магнитных полей происходит отклонение стрелки прибора на определенный угол. Шкала головки для облегчения работы сразу проградуирована в омах. При этом используется выражение сопротивления через ток по формуле 3.
У омметра для обеспечения точных замеров должно поддерживаться стабилизированное значение подаваемого напряжения от батареи питания. С этой целью применяется калибровка посредством использования добавочного регулировочного резистора R рег. С его помощью до начала измерения на схему ограничивается подача излишнего напряжения от источника, выставляется строго стабильная, нормируемая величина.
Определение напряжения с помощью закона Ома
Во время работ с электрическими схемами бывают случаи, когда необходимо узнать падение напряжения на каком-то элементе, например, резисторе, а известно его сопротивление, которое обычно маркируется на корпусе, и проходящий сквозь него ток. Для этого не обязательно подключать вольтметр, а достаточно воспользоваться расчетами по формуле 2.
В нашем случае для рисунка 3 проведем расчеты: U=2,5·4,8 =12 В.
Определение тока с помощью закона Ома
Этот случай описывает формула 3.
 Его используют для расчета нагрузок в электрических схемах, выбора сечений проводников, кабелей, предохранителей или защитных автоматов.
Его используют для расчета нагрузок в электрических схемах, выбора сечений проводников, кабелей, предохранителей или защитных автоматов.В нашем примере расчет выглядит так: I=12/4,8=2,5 А.
Шунтирование
Этот способ в электротехнике используют для исключения работы определенных элементов из схемы без их демонтажа. Для этого на ненужном резисторе замыкают накоротко проводником входящую и отходящую клеммы (на рисунке 1 и 2) — шунтируют.
В результате ток схемы выбирает для себя путь с меньшим сопротивлением через шунт и резко возрастает, а напряжение зашунтированного элемента падает до нуля.
Короткое замыкание
Этот режим является частным случаем шунтирования и, в общем-то, показан на рисунке выше, когда закоротка устанавливается на выходные клеммы источника. При его возникновении создаются очень опасные большие токи, способные поражать людей и сжигать не защищенное электрооборудование.

Для борьбы со случайно возникающими замыканиями в электрической сети используют защиты. На них выставляют такие уставки, которые не мешают работать схеме в нормальном режиме. Они отключают питание только при аварийных случаях.
Например, если ребенок по неосторожности всунет в домашнюю розетку проволоку, то правильно настроенный автоматический выключатель вводного квартирного щита практически моментально отключит электроснабжение.
Все, что описано выше, относится к закону Ома для участка цепи постоянного тока, а не полной схемы, где процессов может быть значительно больше. Следует представлять, что это только небольшая часть применения его в электротехнике.
Закономерности, выявленные знаменитым ученым Георгом Симоном Омом между током, напряжением и сопротивлением по-разному описываются в различных средах и цепях переменного тока: однофазных и трехфазных.
Вот основные формулы, выражающие соотношения электрических параметров в металлических проводниках.
Более сложные формулы для проведения специальных расчетов закона Ома на практике.
Как видим, исследования, которые провел гениальный ученый Георг Симон Ом, имеют огромное значение даже в наше время бурного развития электротехники и автоматики.
Основные электрические законы. Применение закона ома на практике
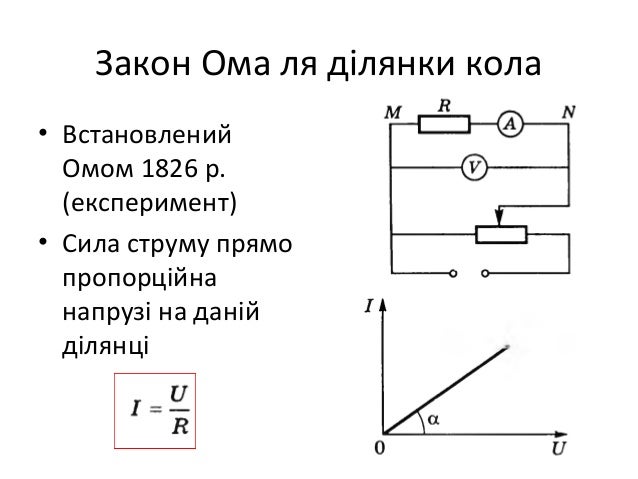
Закон ОмаНемецкий физик Георг Ом (1787 -1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорционально напряжению U на концах проводника:
где R – .
Уравнение (1) выражает закон Ома для участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорционально сопротивлению проводника.

Участок цепи, в котором не действуют э.д.с. (сторонние силы) называют однородным участком цепи, поэтому эта формулировка закона Ома справедлива для однородного участка цепи.
Подробнее смотрите здесь:
Теперь рассмотрим неоднородный участок цепи, где действующую э.д.с. на участке 1 – 2 обозначим через Ε12, а приложенную на концах участка – через φ1 – φ2.
Если ток проходит по неподвижным проводникам, образующим участок 1-2, то работа A12 всех сил (сторонних и электростатических), совершаемая над носителями тока, по равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда Q0 на участке 1- 2: A12 = Q0E12 + Q0(φ1 – φ2) (2)
Э.д.с. E12, как и I, – величина скалярная. Её необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если е.д.с. способствует движению положительных зарядов в выбранном направлении (в направлении 1-2), то E12 > 0. Если э.д.с. препятствует движению положительных зарядов в данном направлении, то E12 За время t в проводнике выделяется теплота:
Q =I 2 Rt = IR(It) = IRQ0 (3)
IR = (φ1 – φ2) + E12 (4)
I = (φ1 – φ2 + E12) / R (5)
Если на данном участке цепи источник тока отсутствует (E12 = 0), то из (5) приходим к закону Ома для однородного участка цепи
Если же замкнута, то выбранные точки 1 и 2 совпадают, φ1 = φ2; тогда из (5) получаем закон Ома для замкнутой цепи:
I = E / R,
I = E / (r+R1).
Примеры расчетов по закону Ома:
Закон
Ома для участка цепи: сила
тока I на участке электрической цепи прямо
пропорциональна напряжению U на концах участка и обратно пропорциональна
его сопротивлению R.
Формула закона: I =. Отсюда запишем формулыU = IR и R = .
Рис.1. Участок цепи Рис.2. Полная цепь
Закон
Ома для полной цепи: сила
тока I полной электрической цепи равнаЭДС
(электродвижущей силе) источника тока Е ,
деленной на полное сопротивление цепи (R
+ r). Полное
сопротивление цепи равно сумме
сопротивлений внешней цепи R и внутреннего r источника тока.Формула
закона I
=
. На
рис. 1 и 2 приведены схемы электрических
цепей.
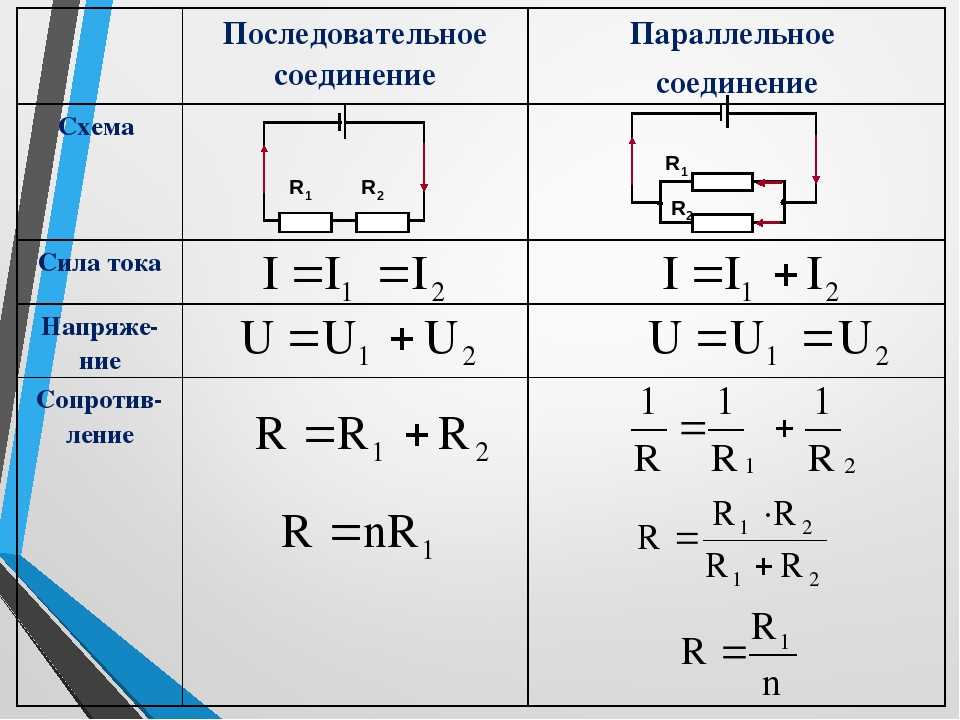
3. Последовательное и параллельное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно . Смешанное соединение сочетает оба эти соединения.
Сопротивление,при
включении которого
вместо всех других проводников,
находящихся между двумя точками цепи,
ток и напряжение остаются неизменными,
называют эквивалентным
сопротивлением этих
проводников.
Последовательное соединение
Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.
Как следует из первого правила Кирхгофа , при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).
1. При последовательном соединении проводников (рис. 1) сила тока во всех проводниках одинакова: I 1 = I 2 = I 3 = I
Рис. 1.Последовательное соединение двух проводников.
2.
Согласно закону Ома, напряженияU 1 иU 2 на
проводниках равны U 1 = IR 1 , U 2 = IR 2 , U 3 = IR 3 .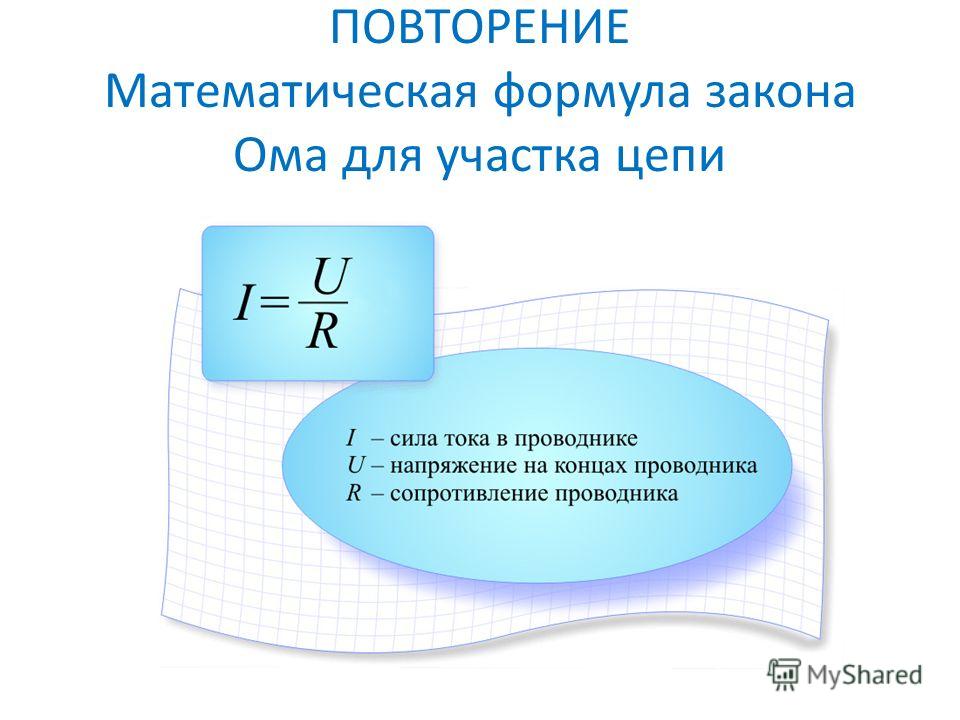
Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.
U = U 1 + U 2 + U 3
Позакону Ома, напряжения U 1, U 2 на проводниках равныU 1 = IR 1 , U 2 = IR 2 , В соответствии вторым правилом Кирхгофа напряжение на всем участке:
U = U 1 + U 2 = IR 1 + IR 2 = I(R 1 + R 2 )= I·R. Получаем: R = R 1 + R 2
Общее напряжение U на проводниках равно сумме напряжений U 1 , U 2 , U 3 равно: U = U 1 + U 2 + U 3 = I · (R 1 + R 2 + R 3 ) = IR
где R ЭКВ – эквивалентное сопротивление всей цепи. Отсюда: R ЭКВ = R 1 + R 2 + R 3
Отсюда: R ЭКВ = R 1 + R 2 + R 3
При последовательном соединении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи: R ЭКВ = R 1 + R 2 + R 3 +…
Этот результат справедлив для любого числа последовательно соединенных проводников.
Из закона Омаследует: при равенстве сил тока при последовательном соединении:
I = , I = . Отсюда = или =, т. е. напряжения на отдельных участках цепи прямо пропорциональны сопротивлениям участков.
При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U 1 на их количество n :
U ПОСЛЕД = n · U 1 .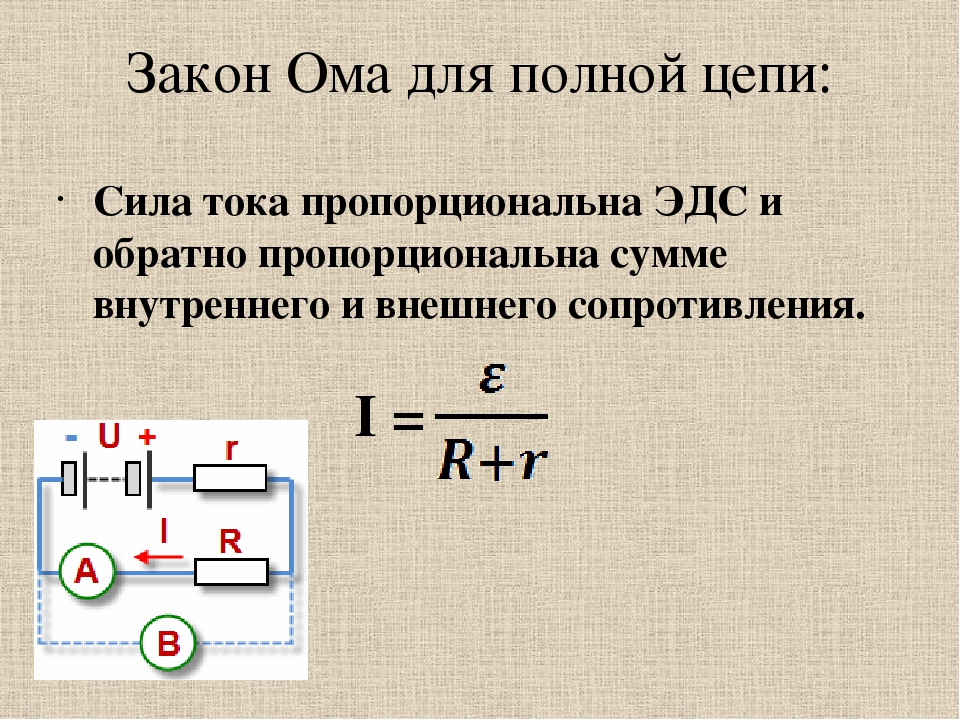 Аналогично
для сопротивлений: R ПОСЛЕД = n · R 1
Аналогично
для сопротивлений: R ПОСЛЕД = n · R 1
При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.
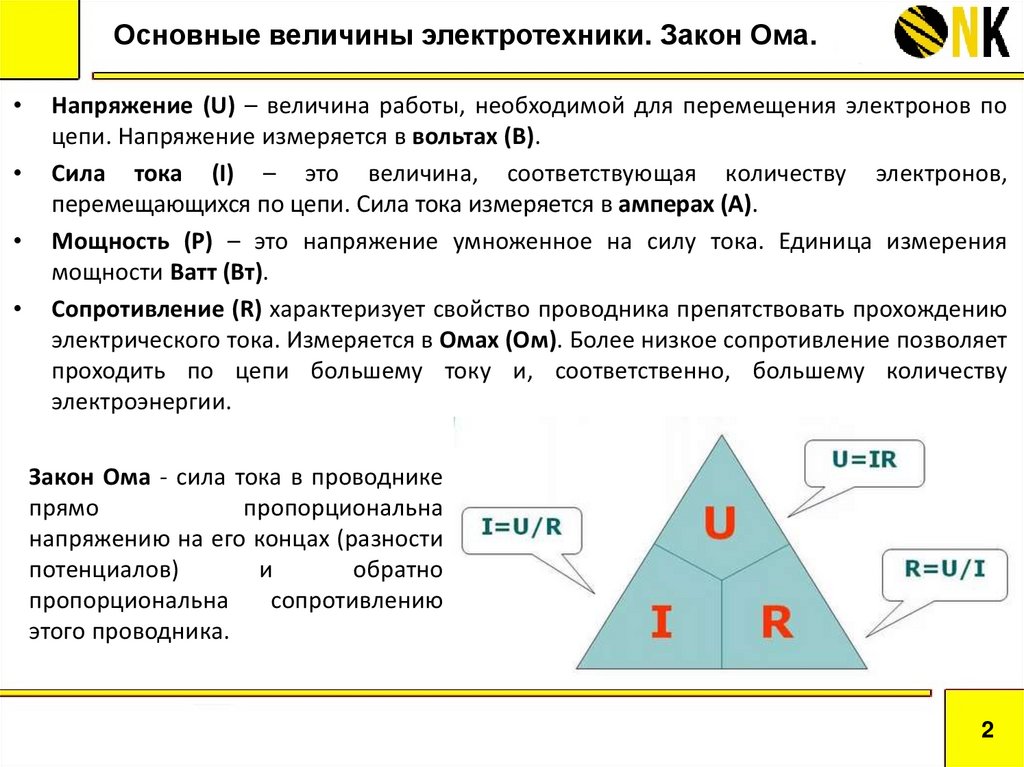
Такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.
Закон Ома
Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома . В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:
«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».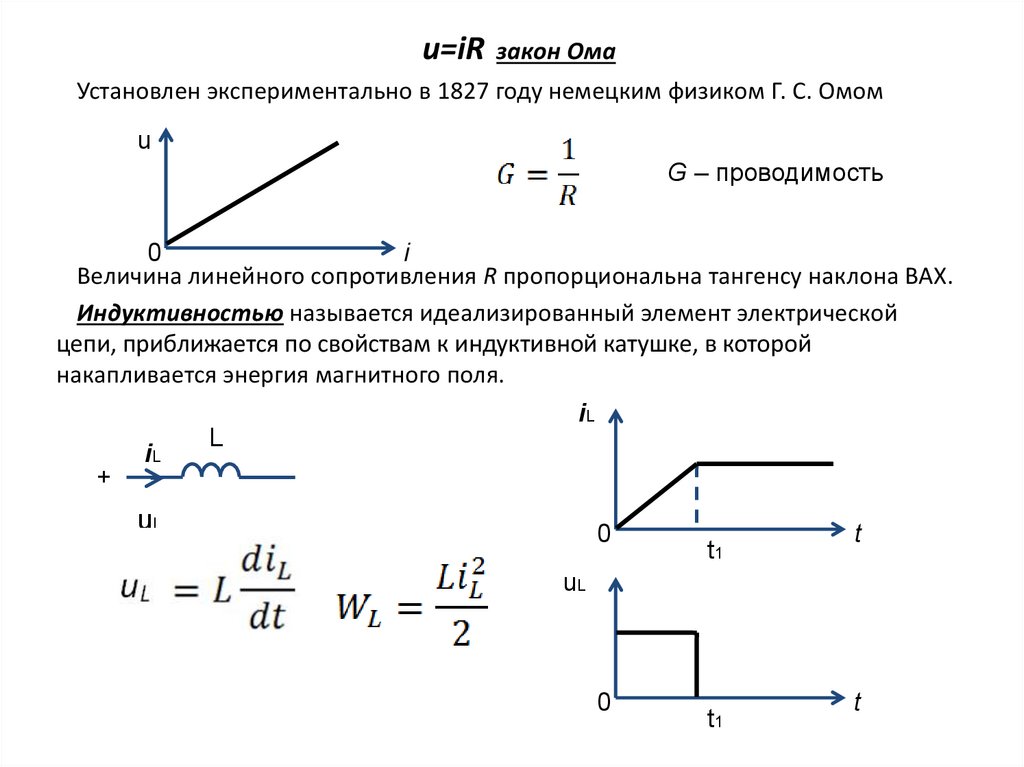
Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.
Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:
В предыдущей статье мы проводили аналогию между электричеством и водой , и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:
На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше).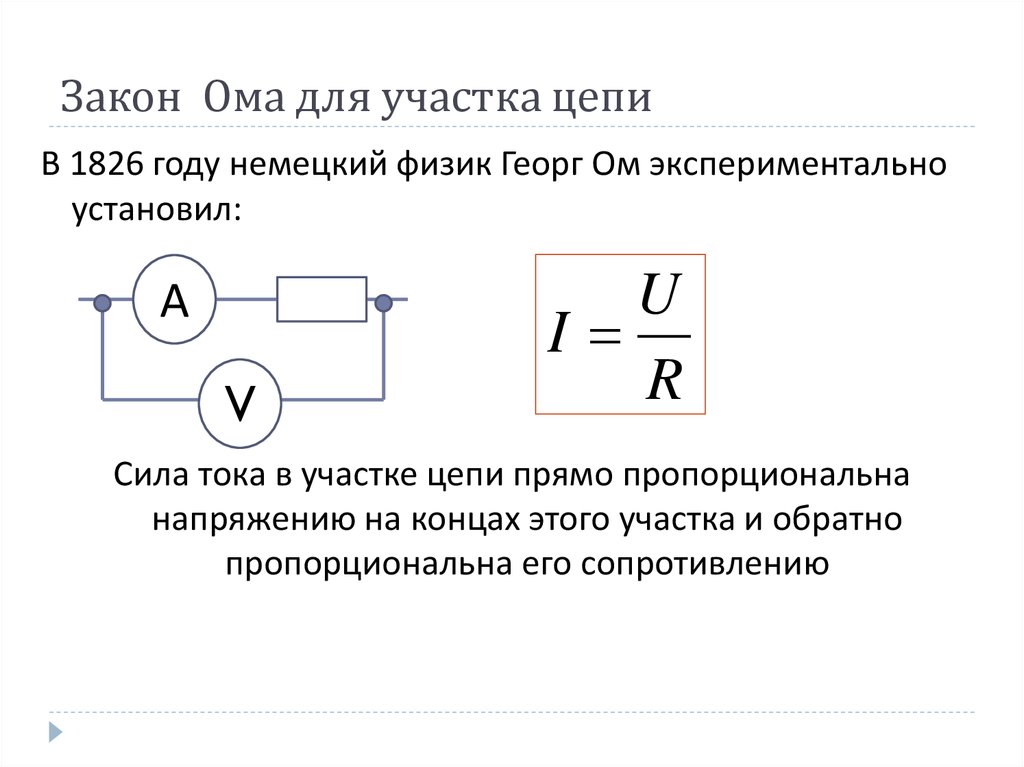 Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка». Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.
Последовательное подключение – последовательная цепь
При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).
А закон Ома в последовательной цепи будет иметь вид:
При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:
Параллельное подключение – параллельная цепь
При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.
Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:
При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления. Или еще говорят, что «сопротивление будет меньше наименьшего».
Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:
Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:
Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.
Электрическая мощность
Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:
Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором. И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно
И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно
Закон Ома часто называют основным законом электричества. Открывший его в 1826 г. известный немецкий физик Георг Симон Ом установил зависимость между основными физическими величинами электрической цепи – сопротивлением, напряжением и силой тока.
Электрическая цепь
Чтобы лучше понять смысл закона Ома, нужно представлять, как устроена электрическая цепь.
Что же такое электрическая цепь? Это путь, который проходят электрически заряженные частицы (электроны) в электрической схеме.
Чтобы в электрической цепи существовал ток, необходимо наличие в ней устройства, которое создавало бы и поддерживало разность потенциалов на участках цепи за счёт сил неэлектрического происхождения. Такое устройство называется источником постоянного тока , а силы – сторонними силами .
Такое устройство называется источником постоянного тока , а силы – сторонними силами .
Электрическую цепь, в которой находится источник тока, называют полной электрической цепью . Источник тока в такой цепи выполняет примерно такую же функцию, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.
Простейшая замкнутая электрическая цепь состоит из одного источника и одного потребителя электрической энергии, соединённых между собой проводниками.
Параметры электрической цепи
Свой знаменитый закон Ом вывел экспериментальным путём.
Проведём несложный опыт.
Соберём электрическую цепь, в которой источником тока будет аккумулятор, а прибором для измерения тока – последовательно включенный в цепь амперметр. Нагрузкой служит спираль из проволоки. Напряжение будем измерять с помощью вольтметра, включенного параллельно спирали. Замкнём с помощью ключа электрическую цепь и запишем показания приборов.
Подключим к первому аккумулятору второй с точно таким же параметрами. Снова замкнём цепь. Приборы покажут, что и сила тока, и напряжение увеличились в 2 раза.
Снова замкнём цепь. Приборы покажут, что и сила тока, и напряжение увеличились в 2 раза.
Если к 2 аккумуляторам добавить ещё один такой же, сила тока увеличится втрое, напряжение тоже утроится.
Вывод очевиден: сила тока в проводнике прямо пропорциональна напряжению, приложенному к концам проводника .
В нашем опыте величина сопротивления оставалась постоянной. Мы меняли лишь величину тока и напряжения на участке проводника. Оставим лишь один аккумулятор. Но в качестве нагрузки будем использовать спирали из разных материалов. Их сопротивления отличаются. Поочерёдно подключая их, также запишем показания приборов. Мы увидим, что здесь всё наоборот. Чем больше величина сопротивления, тем меньше сила тока. Сила тока в цепи обратно пропорциональна сопротивлению .
Итак, наш опыт позволил нам установить зависимость силы тока от величины напряжения и сопротивления.
Конечно, опыт Ома был другим. В те времена не существовало амперметров, и, чтобы измерить силу тока, Ом использовал крутильные весы Кулона. Источником тока служил элемент Вольта из цинка и меди, которые находились в растворе соляной кислоты. Медные проволоки помещались в чашки со ртутью. Туда же подводились концы проводов от источника тока. Проволоки были одинакового сечения, но разной длины. За счёт этого менялась величина сопротивления. Поочерёдно включая в цепь различные проволоки, наблюдали за углом поворота магнитной стрелки в крутильных весах. Собственно, измерялась не сама сила тока, а изменение магнитного действия тока за счёт включения в цепь проволок различного сопротивления. Ом называл это «потерей силы».
Источником тока служил элемент Вольта из цинка и меди, которые находились в растворе соляной кислоты. Медные проволоки помещались в чашки со ртутью. Туда же подводились концы проводов от источника тока. Проволоки были одинакового сечения, но разной длины. За счёт этого менялась величина сопротивления. Поочерёдно включая в цепь различные проволоки, наблюдали за углом поворота магнитной стрелки в крутильных весах. Собственно, измерялась не сама сила тока, а изменение магнитного действия тока за счёт включения в цепь проволок различного сопротивления. Ом называл это «потерей силы».
Но так или иначе эксперименты учёного позволили ему вывести свой знаменитый закон.
Георг Симон Ом
Закон Ома для полной цепи
Между тем, формула, выведенная самим Омом, выглядела так:
Это не что иное, как формула закона Ома для полной электрической цепи: « Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений внешней цепи и внутреннего сопротивления источника ».
В опытах Ома величина Х показывала изменение величины тока. В современной формуле ей соответствует сила тока I , протекающего в цепи. Величина а характеризовала свойства источника напряжения, что соответствует современному обозначению электродвижущей силы (ЭДС) ε . Значение величины l зависело от длины проводников, соединявших элементы электрической цепи. Эта величина являлась аналогией сопротивления внешней электрической цепи R . Параметр b характеризовал свойства всей установки, на которой проводился опыт. В современной обозначении это r – внутреннее сопротивление источника тока.
Как выводится современная формула закона Ома для полной цепи?
ЭДС источника равна сумме падений напряжений на внешней цепи (U ) и на самом источнике (U 1 ).
ε = U + U 1 .
Из закона Ома I = U / R следует, что U = I · R , а U 1 = I · r .
Подставив эти выражения в предыдущее, получим:
ε = I · R + I · r = I · (R + r) , откуда
По закону Ома напряжение во внешней цепи равно произведению силы тока на сопротивление. U = I · R . Оно всегда меньше, чем ЭДС источника. Разница равна величине U 1 = I · r .
Что происходит при работе батарейки или аккумулятора? По мере того, как разряжается батарейка, растёт её внутренне сопротивление. Следовательно, увеличивается U 1 и уменьшается U .
Полный закон Ома превращается в закон Ома для участка цепи, если убрать из него параметры источника.
Короткое замыкание
А что произойдёт, если сопротивление внешней цепи вдруг станет равно нулю? В повседневной жизни мы можем наблюдать это, если, например, повреждается электрическая изоляция проводов, и они замыкаются между собой. Возникает явление, которое называется коротким замыканием . Ток, называемый током короткого замыкания , будет чрезвычайно большим. При этом выделится большое количество теплоты, которое может привести к пожару. Чтобы этого не случилось, в цепи ставят устройства, называемые предохранителями. Они устроены так, что способны разорвать электрическую цепь в момент короткого замыкания.
Закон Ома для переменного тока
В цепи переменного напряжения кроме обычного активного сопротивления встречается реактивное сопротивление (ёмкости, индуктивности).
Для таких цепей U = I · Z , где Z – полное сопротивление, включающее в себя активную и реактивную составляющие.
Но большим реактивным сопротивлением обладают мощные электрические машины и силовые установки. В бытовых приборах, окружающих нас, реактивная составляющая настолько мала, что её можно не учитывать, а для расчётов использовать простую форму записи закона Ома:
I = U / R
Мощность и закон Ома
Ом не только установил зависимость между напряжением, током и сопротивлением электрической цепи, но и вывел уравнение для определения мощности:
P = U · I = I 2 · R
Как видим, чем больше ток или напряжение, тем больше мощность . Так как проводник или резистор не является полезной нагрузкой, то мощность, которая приходится на него, считается мощностью потерь. Она идёт на нагревание проводника. И чем больше сопротивление такого проводника, тем больше теряется на нём мощности. Чтобы уменьшить потери от нагревания, в цепи используют проводники с меньшим сопротивлением. Так делают, например, в мощных звуковых установках.
И чем больше сопротивление такого проводника, тем больше теряется на нём мощности. Чтобы уменьшить потери от нагревания, в цепи используют проводники с меньшим сопротивлением. Так делают, например, в мощных звуковых установках.
Вместо эпилога
Небольшая подсказка для тех, кто путается и не может запомнить формулу закона Ома.
Разделим треугольник на 3 части. Причём, каким образом мы это сделаем, совершенно неважно. Впишем в каждую из них величины, входящие в закон Ома – так, как показано на рисунке.
Закроем величину, которую нужно найти. Если оставшиеся величины находятся на одном уровне, то их нужно перемножить. Если же они располагаются на разных уровнях, то величину, расположенную выше, необходимо разделить на нижнюю.
Закон Ома широко применяется на практике при проектировании электрических сетей в производстве и в быту.
В 1826 году немецкий ученый Георг Ом совершил открытие и описал
эмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.
Впоследствии, по имени ученого он стал называться закон Ома.
В дальнейшем выяснилось, что эти особенности не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством. Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока.
Закон Ома для участка цепи
Согласно обобщенному закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.
Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.
Беря во внимание вышеприведенную формулу, есть возможность найти неизвестные значенияUиR, сделав несложные математические операции.
Данные выше формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.
Закон Ома для замкнутой цепи
Сила тока полной цепи равна ЭДС, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Замкнутая сеть имеет одновременно сопротивления внутреннего и внешнего характера. Поэтому формулы отношения будут уже другими.
Где E – электродвижущая сила (ЭДС), R- внешнее сопротивление источника, r-внутреннее сопротивление источника.
Закон Ома для неоднородного участка цепи
Замкнутая электрическая сеть содержит участки линейного и нелинейного характера. Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = f1 – f2 + E/ R
Где f1 – f2 – разница потенциалов на конечных точках рассматриваемого участка сети
R – общее сопротивление нелинейного участка цепи
ЭДС нелинейного участка цепи бывает больше нуля или меньше. Если направление движения тока, идущего из источника с движением тока в электрической сети, совпадают, будет преобладать движение зарядов положительного характера и ЭДС будет положительная. В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
Закон Ома для переменного тока
При имеющейся в сети емкости или инертности, необходимо учитывать при проводимых вычислениях, что они выдают свое сопротивление, от действия которого ток приобретает переменный характер.
Закон Ома для переменного тока выглядит так:
где Z – сопротивление по всей длине электрической сети. Его еще называют импеданс. Импеданс составляют сопротивления активного и реактивного характера.
Закон Ома не является основным научным законом, а лишь эмпирическим отношением, причем в некоторых условиях оно может не соблюдаться:
- Когда сеть обладает высокой частотой, электромагнитное поле меняется с большой скоростью, и при расчетах необходимо учитывать инертность носителей заряда;
- В условиях низкой температуры с веществами, которые обладают сверхпроводимостью;
- Когда проводник сильно нагревается проходящим напряжением, отношение тока к напряжению становится переменным и может не соответствовать общему закону;
- При нахождении под высоким напряжением проводника или диэлектрика;
- В светодиодных лампах;
- В полупроводниках и полупроводниковых приборах.

В свою очередь элементы и проводники, соблюдающие закон Ома, называются омическими.
Закон Ома может дать объяснение некоторым явлениям природы. Например, когда мы видим птиц, сидящих на высоковольтных проводах, у нас возникает вопрос – почему на них не действует электрический ток? Объясняется это довольно просто. Птицы, сидя на проводах, представляют собой своеобразные проводники. Большая часть напряжения приходится на промежутки между птицами, а та доля, что приходится на сами «проводники» не представляет для них опасности.
Но это правило работает лишь при единичном соприкосновении. Если птица заденет клювом или крылом провод или телеграфный столб, она неминуемо погибнет от огромного количества напряжения, которое несут в себе эти участки. Такие случаи происходят повсеместно. Поэтому в целях безопасности в некоторых населенных пунктах установлены специальные приспособления, защищающие птиц от опасного напряжения. На таких насестах птицы находятся в полной безопасности.
Закон Ома также широко применятся на практике. Электричество смертельно опасно для человека при одном лишь касании к оголенному проводу. Но в некоторых случаях сопротивление человеческого тела может быть разным.
Так, например, сухая и неповрежденная кожа обладает большим сопротивлением к воздействию электричества нежели рана или кожа, покрытая потом. В следствие переутомления, нервного напряжения и опьянения, даже при небольшом напряжении тока человек может получить сильный удар током.
В среднем, сопротивление тела человека – 700 Ом, значит, для человека является безопасным напряжение в 35 В. Работая с большим напряжением, специалисты используют .
Учебное пособие по закону Омас простыми практическими задачами -…
Опубликовано
Закон Ома является основополагающим уравнением в основных схемах и поражает своей простотой и использованием. В этом уроке мы узнаем, что такое закон Ома, где вы можете и не можете его использовать, и рассмотрим несколько практических примеров закона Ома очень, очень простых схем.
В этом уроке мы узнаем, что такое закон Ома, где вы можете и не можете его использовать, и рассмотрим несколько практических примеров закона Ома очень, очень простых схем.
Закон Ома устанавливает связь между напряжением и током через линейное сопротивление. В учебнике, определяющем и связывающем напряжение, ток, сопротивление и мощность, мы использовали воду в качестве примера. Размышляя об этой аналогии, неудивительно, что существует математическая зависимость между тем, сколько воды течет, в зависимости от высоты водяного столба и размера трубы. Для электричества это соотношение устанавливается как:
или
Несколько важных замечаний:
- Это означает, что напряжение, деленное на сопротивление, дает ток. Или высота воды, деленная на размер трубы, дает вам расход воды. Интуитивно это должно иметь смысл. По мере того, как вы переходите к более высокому потенциалу, больше тока будет течь. Если вы увеличите размер трубы, уменьшив сопротивление, будет течь больший ток.
 И обратное верно.
И обратное верно. - Это линейное уравнение. Это не только означает, что зависимость представляет собой прямую линию, но если вы имеете дело с чем-то нелинейным, где сопротивление изменяется в зависимости от напряжения, это уравнение неприменимо. Это необычно, поэтому мы будем считать резисторы линейными, если явно не указано иное.
- Это верно, когда у вас есть напряжение и сопротивление (обычно резистор), но, когда мы узнаем о других компонентах и источниках питания, этот закон обычно не применяется к ним.
- Обычно напряжение поступает от батарей, настенных розеток и других подобных мест. Резисторы — это электронные компоненты, изготовленные для определенных целей. Наш друг CircuitBread, компания Ohmite, создает множество пассивных компонентов, таких как резисторы. Они могут выглядеть очень, очень по-разному, с более типичными резисторами, похожими на резисторы OC Ohmite, хотя их серия ARCOL довольно известна своим вариантом с более высокой мощностью, но я даже лично видел их сильноточные, низкоомные серии 280 в лифтовые приложения.
 Все они выглядят совершенно по-разному, но используются для их сопротивления.
Все они выглядят совершенно по-разному, но используются для их сопротивления.
Напряжение и ток могут быть как положительными, так и отрицательными. Как упоминалось в предыдущем уроке, напряжение является относительным, поэтому отрицательное напряжение имеет более низкий потенциал, чем то, что (возможно, произвольно) установлено как ноль вольт или заземление. Ток, будучи мерой потока, бывает положительным или отрицательным в зависимости от того, каким образом вы или проблема назначаете поток. Если вы говорите, что ток течет от А к В, а на самом деле ток течет от В к А, то этот ток отрицательный. Однако, если вы посмотрите на ту же ситуацию и определите, что ток течет от B к A, тогда, когда ток действительно течет от B к A, это положительный ток! Поначалу это может сбивать с толку, и оба они до сих пор сбивают меня с толку, если я какое-то время не решал никаких проблем со схемой. Самое главное, чтобы они были прямыми, — это сделать ваши предположения о потенциале напряжения и протекании тока и убедиться, что используемые вами уравнения соответствуют этим предположениям.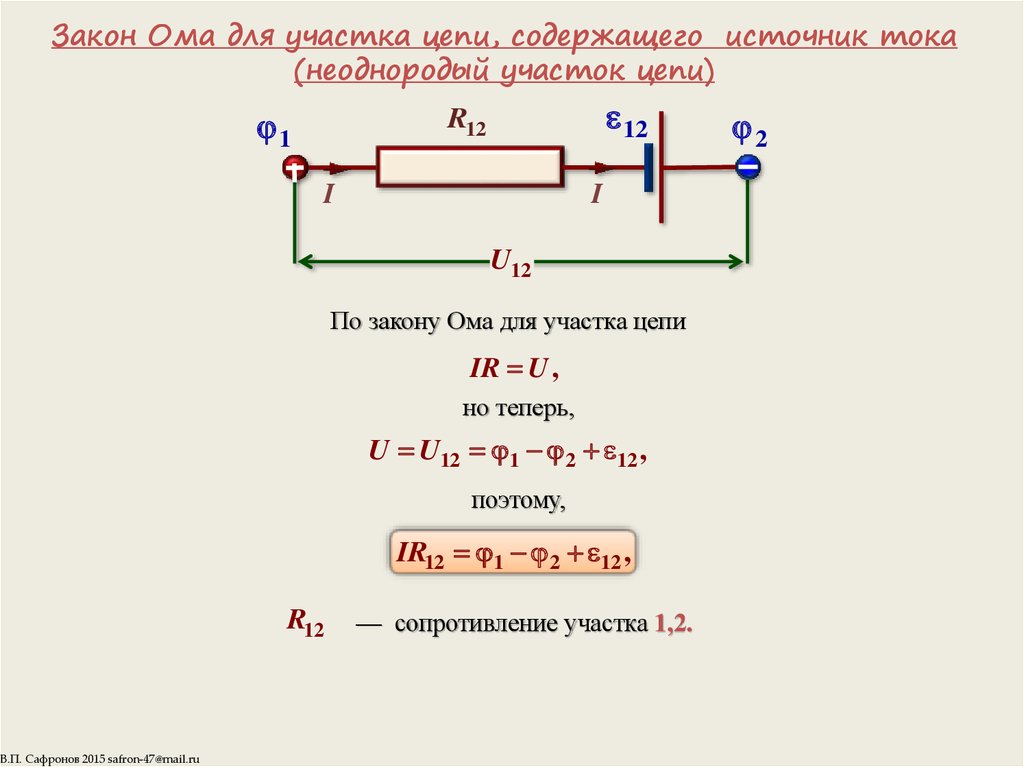 Мы рассмотрим эту концепцию в некоторых практических задачах в конце этого урока.
Мы рассмотрим эту концепцию в некоторых практических задачах в конце этого урока.
Есть две распространенные крайности, которые вы можете увидеть в законе Ома в отношении сопротивления. Когда сопротивление равно нулю и когда сопротивление бесконечно. Когда сопротивление равно нулю, в основном, когда провод соединяет два разных потенциала напряжения, это называется коротким замыканием. Это замыкает напряжения вместе. Глядя на закон Ома, когда сопротивление равно нулю, если у вас есть какое-либо конечное напряжение, вы получите бесконечный ток. Хотя в реальной жизни не существует такой вещи, как бесконечный ток, если это не запланировано, ток будет достаточно высоким, чтобы нанести некоторый ущерб!
Другая крайность — когда сопротивление бесконечно, или когда два потенциала напряжения полностью и полностью разделены. В зависимости от обстоятельств иногда вы можете рассматривать чрезвычайно высокие сопротивления как бесконечно большие, но используйте это предположение с осторожностью. Когда сопротивление бесконечно, это означает, что при любом напряжении ток отсутствует. Если это желательно, то отлично. Если нет, это обычно означает, что то, что ожидает силы, не получает ее.
Когда сопротивление бесконечно, это означает, что при любом напряжении ток отсутствует. Если это желательно, то отлично. Если нет, это обычно означает, что то, что ожидает силы, не получает ее.
Осевые резисторы
Лучший способ учиться — экспериментировать. Вы можете приобрести резисторы от Ohmite, чтобы проверить эти уравнения в реальной жизни.
Купить онлайн
ОТ Ohmite
Заключительные замечания
Иногда вы будете слышать о двух связанных, но разных терминах. Первым из этих терминов является удельное сопротивление. Удельное сопротивление является свойством материала и является основой сопротивления. Материал с высокой проводимостью будет иметь очень низкое удельное сопротивление (например, медь), в то время как материал с высокой изоляцией будет иметь очень высокое удельное сопротивление (например, резина). Большинство материалов, используемых для резистора, будут где-то посередине. Зная длину и площадь поперечного сечения материала, можно умножить удельное сопротивление на длину и разделить на площадь поперечного сечения.
R – Сопротивление (Ом)
ρ – Удельное сопротивление (Ом-см или Ом-м)
l – Длина (см или м)
A – Площадь поперечного сечения (см 2 или m 2 )
Если вы на минутку взглянете на это уравнение, оно станет интуитивно понятным. По мере увеличения длины сопротивление будет расти. Если увеличить площадь, через которую могут пройти электроны, сопротивление уменьшится. Глядя на регулируемый резистор мощности Ohmite серии 210, вы заметите, что сопротивление снижается при уменьшении длины. Изменение площади поперечного сечения не является разумным или простым изменением, поэтому это не вариант с регулируемым резистором. Как видите, это не просто бесполезная теория.
Второй член — проводимость, Г. Это просто обратная величина сопротивления. Он используется в определенных случаях, но по сравнению с резистентностью встречается крайне редко. Единицы измерения иногда называют «мос» с перевернутым символом омега по сравнению с «омами» с перевернутым символом омега. Иногда их также называют Siemens.
Иногда их также называют Siemens.
Уравнение Ома
С этим вы также получите перевернутый закон Ома:
Пример / Практические задачи по закону Ома
Проблема 1. От узла A: 1000 В до узла B: 0 В, через резистор 100 Ом.
Решение:
В этой первой практической задаче по закону Ома мы определяем падение напряжения на резисторе и составляем уравнение. Узел A — 1000 вольт, а узел B — 0 вольт, поэтому мы можем составить уравнение как 1000V — 0V, а затем разделить его на сопротивление, которое равно 100 Ом. Таким образом, мы получаем:
Итак, мы получаем 10 А тока, протекающего от узла A к узлу B.
Проблема 2. Узел A: 12 В к узлу B: 3 В через резистор 200 Ом.
Решение:
В этой второй практической задаче мы выполняем те же шаги, что и в первой задаче, но с другими номерами. Мы смотрим на падение напряжения от узла A к узлу B и устанавливаем первую часть уравнения, которая составляет 12–3 В. Разделив его на сопротивление, мы получим окончательное уравнение:
Разделив его на сопротивление, мы получим окончательное уравнение:
В этом случае мы получим 45 миллиампер, протекающих от узла А к узлу Б. .
Решение:
В этой третьей практической задаче из-за того, что мы по-прежнему используем термины «узел А» и «узел Б», мы по-прежнему составим уравнения относительно потока, идущего от узла А к узлу Б, хотя, по результатам проверки, мы можем сказать, что узел B имеет более высокий потенциал напряжения. Ничего страшного, потому что, пока мы все помечаем правильно, ответ все равно будет правильным. Итак, у нас есть 16 В – 24 В, а затем разделите это на 800 Ом.
Итак, мы получаем отрицательные 10 миллиампер от узла A к узлу B. Это имеет смысл, поскольку узел B находится под более высоким напряжением, поэтому, если мы определим ток, идущий от A к B, если ток равен на самом деле идет от B к A, тогда ток отрицательный.
Проблема 4. Узел A: -7 В к узлу B: -13 В, через резистор 1,2 кОм.
Решение:
В этой четвертой и последней практической задаче, которую мы собираемся решить, мы по-прежнему определим задачу с точки зрения тока, протекающего от узла А к узлу Б. Итак, еще раз мы составляем уравнение. (-7 – (-13))/1200.
Итак, еще раз мы составляем уравнение. (-7 – (-13))/1200.
Обратите внимание: поскольку мы были последовательны в определении вещей, мы знаем, что единственное изменение этой задачи по сравнению с тремя последними задачами заключается в том, что мы вычитаем отрицательное число, таким образом, складывая его. Опять же, поскольку напряжения относительны, фактические напряжения не так важны, как разница между ними. Если вы хотите убедиться в этом сами, повторите эту задачу с узлом A на 6 В и узлом B на 0 В.
Резюме
Закон Ома лежит в основе большинства анализов цепей и довольно прост, если вы внимательно следите за тем, чтобы способ, которым вы устанавливаете свои уравнения, соответствовал тому, как вы назначили полярности и потоки в программа.
Короткие замыкания и разомкнутые цепи — чрезвычайно распространенные сценарии как в академических кругах, так и в реальной жизни, поэтому полезно сделать это второй натурой для вашего понимания цепей.
Далее мы узнаем о ветвях, узлах и циклах, а также о том, как компоненты могут быть расположены последовательно и параллельно. Это позволит нам применять закон Ома к значительно более широкому и более практичному набору практических цепей.
Чтобы узнать больше о резисторах, ознакомьтесь с этим руководством.
Чтобы узнать больше о переменных резисторах или потенциометрах, ознакомьтесь с этим руководством.
Автор:
Джош Бишоп
Интересуясь встраиваемыми системами, туризмом, кулинарией и чтением, Джош получил степень бакалавра электротехники в Университете штата Бойсе. Проработав несколько лет офицером CEC (Seabee) в ВМС США, Джош уволился и в конце концов начал работать над CircuitBread с кучей замечательных людей. В настоящее время Джош живет на юге Айдахо с женой и четырьмя детьми.
Создано с нашим другом:
Компания Ohmite является ведущим поставщиком резистивных изделий для сильноточных, высоковольтных и высокоэнергетических приложений.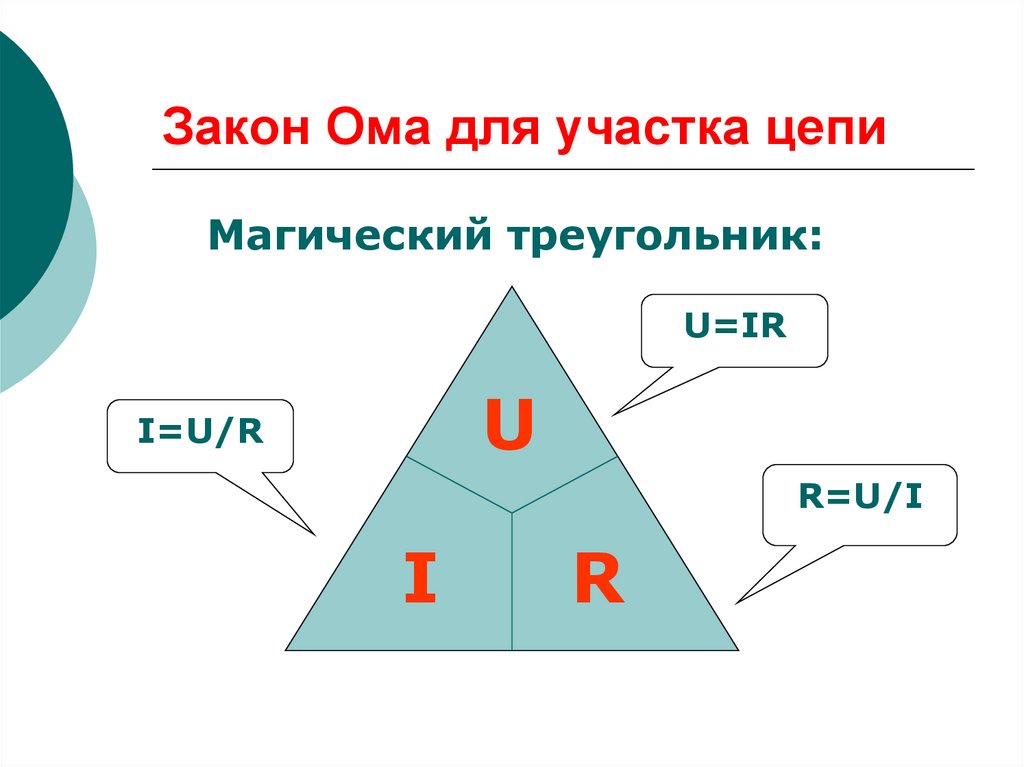 Калькулятор закона Ома
Калькулятор закона Ома
Социальная сеть друзей
- YouTube
- Линкедин
Получите новейшие инструменты и учебные пособия, только что из тостера.
Закон Ома – AP Физика 2
Все ресурсы AP Physics 2
6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
AP Physics 2 Help » Электричество и магнетизм » Схемы » Свойства цепи » Закон Ома
Каков ток через батарею в приведенной выше цепи?
Возможные ответы:
Правильный ответ:
Пояснение:
Сначала найдите общее сопротивление цепи. Поскольку резисторы включены параллельно, используйте следующую формулу:
Подставьте известные значения.
Затем используйте закон Ома, чтобы найти ток.
Подставьте известные значения.
Сообщить об ошибке
Последовательно подключены 3 резистора. Их сопротивления по порядку , , и . Общее падение потенциала равно . Чему равно падение потенциала на втором резисторе?
Возможные ответы:
Правильный ответ:
Пояснение:
Используйте закон Ома , чтобы найти ток, проходящий через каждый резистор. Так как они включены последовательно, они имеют одинаковую величину тока. Как только мы получим ток, мы можем подключить сопротивление для каждого резистора, чтобы найти его падение потенциала.
Теперь найдите падение потенциала на резисторе.
9Сообщить об ошибке. Каково сопротивление медного провода?
Возможные ответы:
Не хватает информации, чтобы найти сопротивление
Правильный ответ:
Объяснение:
Несмотря на отсутствие резистора, действует закон Ома. Используйте его, чтобы найти сопротивление провода.
Используйте его, чтобы найти сопротивление провода.
Сопротивление медного провода
Сообщить об ошибке
В приведенной выше схеме найдите падение напряжения на .
Возможные ответы:
Ни один из этих
Правильный ответ: 9005 7 7 5 5
Сначала найдите общее сопротивление цепи.
и параллельны, поэтому мы находим эквивалентное сопротивление, используя следующую формулу:
Затем сложите последовательные резисторы вместе.
Используйте закон Ома, чтобы найти силу тока в системе.
Поскольку и параллельны, падение напряжения на них будет одинаковым.
Сообщить об ошибке
В приведенной выше схеме найдите ток через .
Возможные ответы:
Ничего из этого
Пояснение:
Сначала найдите общее сопротивление цепи.
и параллельны, поэтому мы находим их эквивалентное сопротивление по следующей формуле:
Затем сложите последовательные резисторы вместе.
Используйте закон Ома, чтобы найти ток в системе.
Суммарный ток, проходящий через и , должен составлять общий ток, так как они параллельны.
Кроме того, падение напряжения на них должно быть одинаковым, так как они параллельны.
Составьте систему уравнений.
Решить.
Сообщить об ошибке
В приведенной выше схеме найдите ток через .
Возможные ответы:
Ни один из этих
Правильный ответ: 9005 7 7 5 5
Сначала найдите общее сопротивление цепи.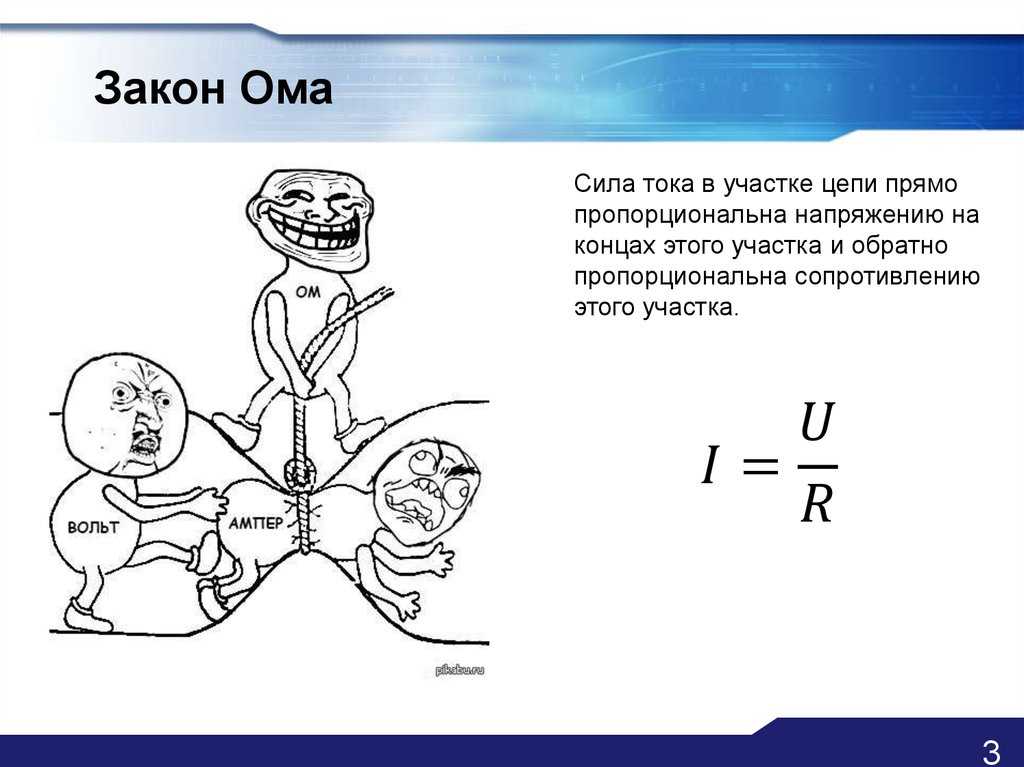
и параллельны, поэтому мы находим их эквивалентное сопротивление, используя следующую формулу:
Затем сложите последовательно резисторы.
Используйте закон Ома, чтобы найти ток в системе.
При последовательном соединении все резисторы будут иметь одинаковый ток.
Таким образом, ток через такой же, как и через остальную часть цепи.
Сообщить об ошибке
В приведенной выше схеме найдите падение напряжения на .
Возможные ответы:
Ничего из этого Пояснение:
Сначала найдите общее сопротивление цепи.
и параллельны, поэтому мы находим их эквивалентное сопротивление по следующей формуле:
Затем последовательно сложите резисторы.
Используйте закон Ома, чтобы найти ток в системе.
и будет иметь одинаковое падение напряжения на них, как и они параллельно, и эквивалентны комбинированному резистору
Отчет о ошибке
. , найти падение напряжения на .
Возможные ответы:
Ничего из этого Пояснение:
Сначала найдите общее сопротивление цепи.
и параллельны, поэтому мы находим их эквивалентное сопротивление, используя следующую формулу:
Затем сложите последовательно резисторы.
Используйте закон Ома, чтобы найти ток в системе.
и будет иметь одинаковое падение напряжения на них, как и они параллельно и эквивалентны комбинированному резистору
Отчет о ошибке
Что является общим сопротивление цепи?
Возможные ответы:
Ни один из этих
Правильный ответ:
Объяснение:
, , и параллельны, поэтому мы добавляем их, используя:
Мы находим, что
, , и последовательно.


