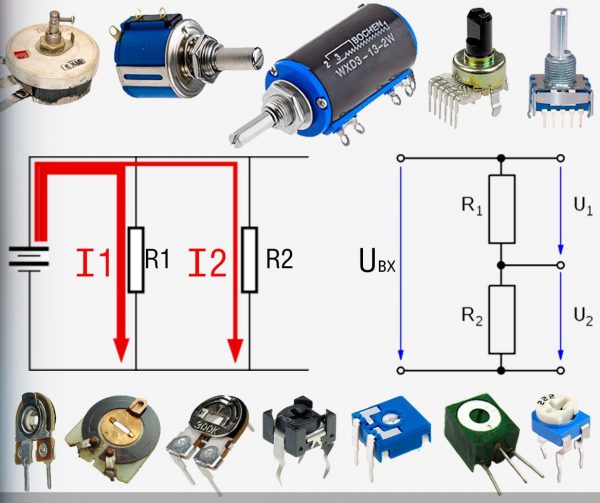
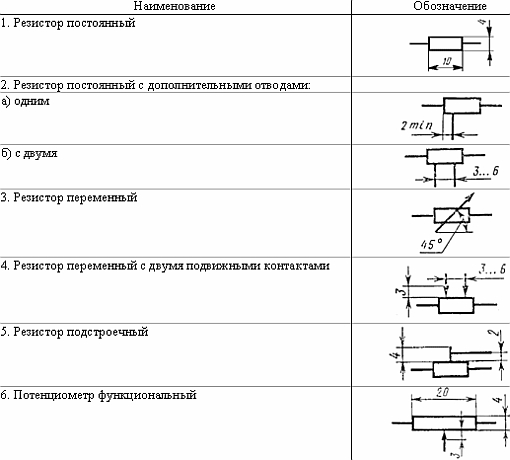
Резистор схема: Резисторы: описание, подключение, схема, характеристики

Содержание

Схемы соединения резисторов

Последовательное соединение резисторов

I_общ = I₁ = I₂ = I₃

U_общ = U₁ + U₂ + U₃

Параллельное соединение резисторов

I_общ = I₁ + I₂ + I₃

U_общ = U₁ = U₂ = U₃

Реостат

Реостат – это переменный резистор, который включается в цепь последовательно с потребителем нагрузки.

Изменяя положение ползунка, в цепи меняется ток от 0 до max.

Реостат применяется для изменения тока в цепи.

В электрических схемах встречается понятие – реостатное включение нагрузки.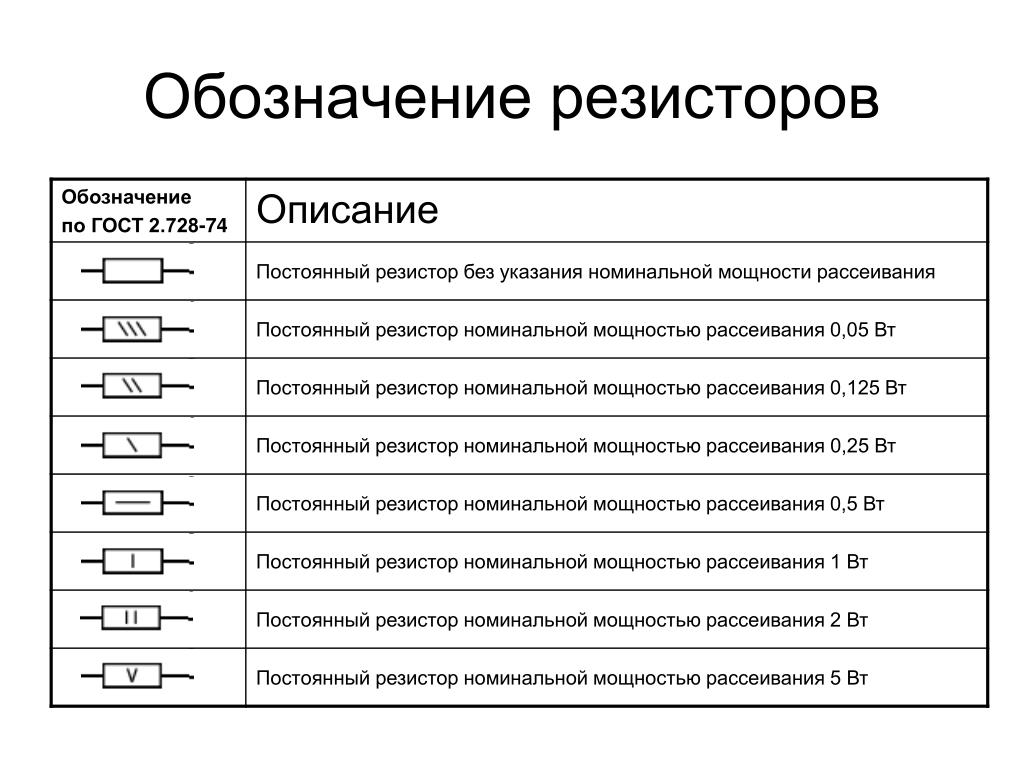

Реостатное включение нагрузки

T₁ I =

U_ист

R_р + R_н

→ max

R_P = 0

T₂ I =

U_ист

R_р + R_н

→ min

Гасящий резистор

В радиосхемах возникает необходимость подавать на потребитель напряжение меньше чем развивает источник, тогда между источником и нагрузкой включается гасящий резистор.

Применение – в схеме создания напряжения смещения на участке эмиттер-база транзистора.

Гасящий резистор

U_гас = U_ист – U_Rн

P_Rгас = I² – R_гас

Делитель напряжения

Делитель напряжения – это цепь, состоящая из нескольких последовательно соединённых резисторов обеспечивающих подачу на потребитель некоторой части напряжения источника.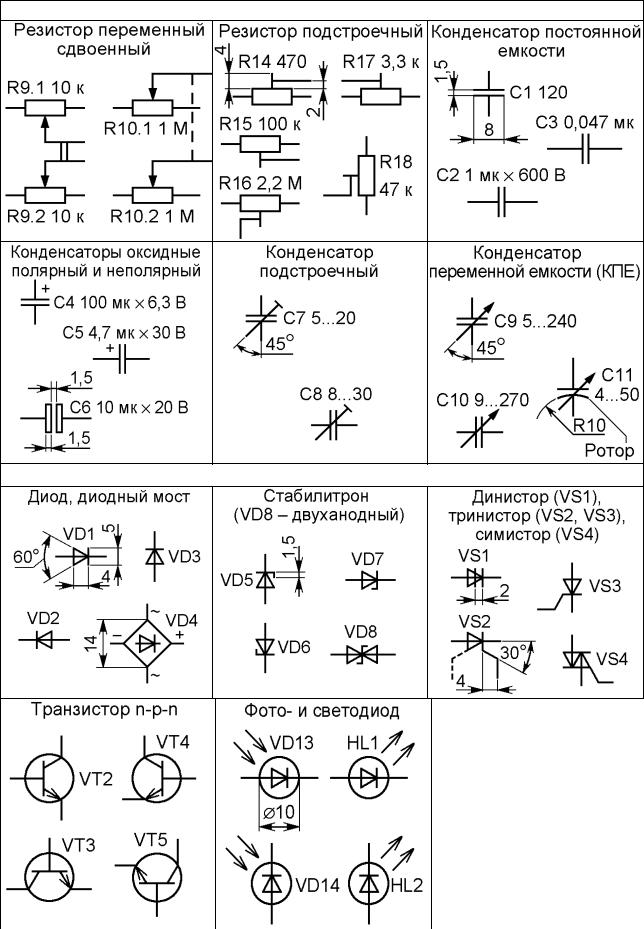

Потенциометр

Потенциометр – это переменный резистор, с части которого снимается напряжения источника.

Потенциометр

Применение – регулировка громкости на входе усилителя низкой частоты.

Схемы защиты ТН от феррорезонанса

Скачать опросные листы на трансформаторы напряжения

Скачать каталог на трансформаторы (pdf; 32 Мб)

Скачать каталог на трансформаторы ТВ (pdf; 3,5 Мб)

Скачать каталог “Трансформаторы для железных дорог” (pdf; 4,8 Мб)

Варианты схем, разработанных конструкторами ОАО «СЗТТ» для защиты трансформаторов напряжения от феррорезонанса.

№ п/п	Схема защиты от феррорезонанса	Схема включения	Краткое описание и преимущества применения
1	Антирезонансная трехфазная группа 3хЗНОЛ(П) однофазных, заземляемых трансформаторов с заземлением нейтрали через высокоомные резисторы.		Антирезонансная трехфазная группа 3хЗНОЛ(П) с заземлением нейтрали через высокоомные резисторы – это самая распространенная схема защиты трансформаторов напряжения от феррорезонанса, которая применяется в сетях на класс напряжения (6-10) кВ. Для повышения устойчивости к феррорезонансу и воздействию перемежающейся дуги в дополнительные обмотки, соединенные в разомкнутый треугольник, используемые для контроля изоляции сети, рекомендуется включать резистор сопротивлением 25 Ом, рассчитанный на длительное протекание тока 4 А. Также трехфазные группы выпускаются со встроенным защитным предохранителем, что обеспечивает дополнительную защиту обмоток ВН от сверхтоков при феррорезонансе. Применяется как стандартное решение для защиты трансформаторов напряжения от феррорезонанса в сети.
2	Антирезонансная трехфазная группа 3хЗНОЛ(П) однофазных, заземляемых трансформаторов с заземлением нейтрали через высокоомные резисторы и устройством СЗТн.		Антирезонансная трехфазная группа 3хЗНОЛ(П) с заземлением нейтрали через высокоомные резисторы и устройством СЗТн практически не имеет отличий от предыдущего варианта. Отличие лишь в том, что в дополнительные обмотки соединенные в разомкнутый треугольник, используемые для контроля изоляции сети, включаются устройство СЗТн . Устройство можно применять одновременно с защитным реле и сопротивлением 25 Ом. Параллельное подключение не влияет на защитные функции СЗТн. Применение устройства СЗТн значительно повышает антирезонансные свойства трехфазной группы. Применяется как стандартное решение для защиты трансформаторов напряжения от феррорезонанса в сети.
3	Антирезонансная трехфазная группа 3хЗНОЛ.04(П) однофазных, заземляемых трансформаторов с заземлением нейтрали через дополнительный трансформатор напряжения нулевой последовательности.		Антирезонансная трехфазная группа 3хЗНОЛ.04(П) с заземлением нейтрали через реактор состоит из трех однофазных заземляемых трансформаторов напряжения, соединенных в звезду с выведенной нейтралью, и дополнительного трансформатора напряжения нулевой последовательности (ТНП), который включается между нейтралью звезды и землей. Вывод «Х» ТН, входящих в звезду, рассчитан на полную изоляцию, что позволяет испытывать внутреннюю изоляцию ТН полным уровнем приложенного напряжения промышленной частоты. ТНП позволяет измерять напряжение нулевой последовательности , а его большое реактивное сопротивление эффективно предотвращает возникновение устойчивого феррорезонанса. Данная схема для защиты от феррорезонанса является наиболее эффективной, универсальной и может применяться в широком диапазоне ëмкостных параметров сетей, класса напряжения (6-35) кВ.
4	Антирезонансная трехфазная группа 3хНОЛ(П) на базе однофазных незаземляемых трансформаторов напряжения.		Для решения всех вопросов, связанных с эксплуатацией заземляемых трансформаторов напряжения в сетях с изолированной нейтралью разработана трехфазная группа 3хНОЛ-6(10), состоящая из трех незаземляемых трансформаторов, соединенных по схеме треугольник/треугольник. Основное преимущество 3хНОЛ-6(10) – отсутствие заземляемого вывода с ослабленной изоляцией. Это значит, что трансформатор не подвержен влиянию феррорезонанса и не требует дополнительных защит от его воздействия. Внутреннюю изоляцию трансформаторов можно испытывать приложенным одноминутным напряжением промышленной частоты. Возможно изготовление трансформаторов с основной и дополнительной вторичной обмоткой. Дополнительная обмотка предназначена для питания цепей собственных нужд и не является измерительной.
5	Антирезонансная схема с R/C –гасителями.		Антирезонансная схема с R/C – гасителями. В схеме могут быть использованы заземляемые или незаземляемые трансформаторы напряжения. В случае использования заземляемых трансформаторов напряжения, R/C – гасители и трансформаторы напряжения включаются параллельно в сеть, по схеме звезда / звезда. В случае с использованием незаземляемых трансформаторов, R/C – гасители включаются по схеме звезда, трансформаторы напряжения по схеме открытого или полного треугольника. Схемы с R/C – гасителями применяются, как правило, для защиты трансформаторов напряжения от воздействия перенапряжений, низкого качества электрической энергии и других негативных факторов влияющих на надежность трансформаторов напряжения.

Версия для печати (pdf)

Схема 5 разработана совместно с партнером – ООО “Экспертный центр технологических решений” г. Екатеринбург. Подробная информация по ссылке.

Вариант исполнения шкафов с трансформаторами напряжения и RC-гасителями.

При выборе схемы 5 обязательно заполнение опросного листа.

Переменный резистор | Электроника для всех

Вроде бы простая деталька, чего тут может быть сложного? Ан нет! Есть в использовании этой штуки пара хитростей. Конструктивно переменный резистор устроен также как и нарисован на схеме — полоска из материала с сопротивлением, к краям припаяны контакты, но есть еще подвижный третий вывод, который может принимать любое положение на этой полоске, деля сопротивление на части. Может служить как перестариваемым делителем напряжения (потенциометром) так и переменным резистором — если нужно просто менять сопротивление.

Хитрость конструктивная:
Допустим, нам надо сделать переменное сопротивление. Выводов нам надо два, а у девайса их три. Вроде бы напрашивается очевидная вещь — не использовать один крайний вывод, а пользоваться только средним и вторым крайним.

Плохая идея! Почему? Да просто в момент движения по полоске подвижный контакт может подпрыгивать, подрагивать и всячески терять контакт с поверхностью. При этом сопротивление нашего переменного резистора становится под бесконечность, вызывая помехи при настройке, искрение и выгорание графитовой дорожки резистора, вывод настраимого девайса из допустимого режима настройки, что может быть фатально.
Решение? Соединить крайний вывод с средним. В этом случае, худшее что ждет девайс — кратковременное появление максимального сопротивления, но не обрыв.

Борьба с предельными значениями.
Если переменным резистором регулируется ток, например питание светодиода, то при выведении в крайнее положение мы можем вывести сопротивление в ноль, а это по сути дела отстутствие резистора — светодиод обуглится и сгорит. Так что нужно вводить дополнительный резистор, задающий минимально допустимое сопротивление. Причем тут есть два решения — очевидное и красивое 🙂 Очевидное понятно в своей простоте, а красивое замечательно тем, что у нас не меняется максимально возможное сопротивление, при невозможности вывести движок на ноль. При крайне верхнем положении движка сопротивление будет равно (R1*R2)/(R1+R2) — минимальное сопротивление. А в крайне нижнем будет равно R1 — тому которое мы и рассчитали, и не надо делать поправку на добавочный резистор. Красиво же! 🙂

Если надо воткнуть ограничение по обеим сторонам, то просто вставляем по постоянному резистору сверху и снизу. Просто и эффективно. Заодно можно и получить увеличение точности, по принципу приведенному ниже.

Повышение точности.
Порой бывает нужно регулировать сопротивление на много кОм, но регулировать совсем чуть чуть — на доли процента. Чтобы не ловить отверткой эти микроградусы поворта движка на большом резисторе, то ставят два переменника. Один на большое сопротивление, а второй на маленькое, равное величине предполагаемой регулировки. В итоге мы имеем две крутилки — одна «Грубо» вторая «Точно» Большой выставляем примерное значение, а потом мелкой добиваем его до кондиции.

Переменный резистор с ДУ » S-Led.Ru

Система дистанционного управления является неотъемлемым атрибутом любого современного аудиоцентра. Но так было не всегда. У многих любителей музыки остаются в эксплуатации аудиоцентры, усилители ЗЧ, радиолы, магнитофоны, произведенные (или сделанные самостоятельно) не один десяток лет назад. В те времена такое понятие как электронная регулировка было достаточно редким явлением.

В большинстве случаев регуляторы громкости, тембра, баланса строились по пассивным схемам, на переменных резисторах. Обладая очень хорошим качеством звука (не в пример многим современным аппаратам), такая аппаратура практически не пригодна для введения в неё системы дистанционного управления, Дело в том, что система дистанционного управления управляет функциями аппарата либо по цифровой шине, либо изменяя постоянные напряжения.

В обеих случаях требуется какой-то усилитель, имеющий либо цифровой вход управления, либо электронную регулировку усиления путем изменения постоянного напряжения.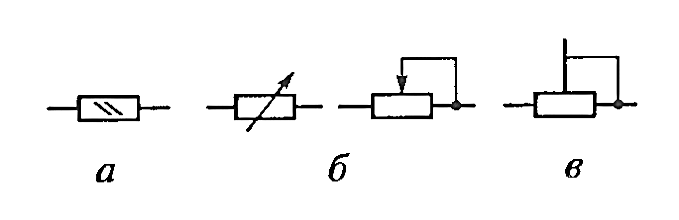 Сейчас в продаже можно встретить множество импортных и отечественных микросхем с такими усилителями. Но, это хорошо только в том случае, если вы конструируете аппарат “с нуля”.

Любое введение дополнительных регулируемых усилителей в уже готовый и отлаженный тракт, в котором применяются пассивные механические регуляторы, приводит к его полной разладке, и требует существенной переделки схемы предварительного усиления (фактически, её замены). Разумеется, “портить”, таким образом, хороший и “любимый” усилитель захочется не каждому, тем более, что нет уверенности в том, что новый предусилитель или старый, но настроенный другим образом, будет работать не хуже прежнего.

В этой связи, реальным выходом из положения, не нарушающим работу прежнего предусилителя, может быть применение электронных аналогов переменных резисторов, представляющих собой цепь постоянных резисторов, точка подключения к которым переключается при помощи аналого-цифровых мультиплексоров.

Такая схема не только полностью имитирует работу переменного резистора, но и путем установки различных сопротивлений на разных ступенях регулировки позволяет задать практически любой закон регулировки, наиболее приемлемый в конкретной схеме предусилителя.

В любительских условиях проще всего за основу для системы дистанционного управления взять комплект модулей ДУ, предназначенный для модернизации советских телевизоров серии УСЦТ. Такие комплекты сейчас часто можно встретить в продаже, они неоднократно описывались в разной литературе и, поэтому, их схемотехника широко известна радиолюбителям.

Выходные сигналы такой системы ДУ, это выходы ЦАП, на которых меняются постоянные напряжения при нажатии кнопок регулировки, выход выключателя сетевого питания и восемь выходов для переключения программ телевизора. Нам нужны именно эти восемь выходов. Они дадут возможность управлять четырьмя электронными переменными резисторами, по два выхода “уменьшить” и “увеличить” на каждый. В связи с тем, что эти выходы системы ДУ телевизора должны работать совместно с восьмипрограммной системой переключения программ УСУ-1-15, они сделаны так, что на каждом из выходов появляется логическая единица только во время нажатия соответствующей кнопки пульта, и переходит в высокоомное состояние при отпускании кнопки пульта.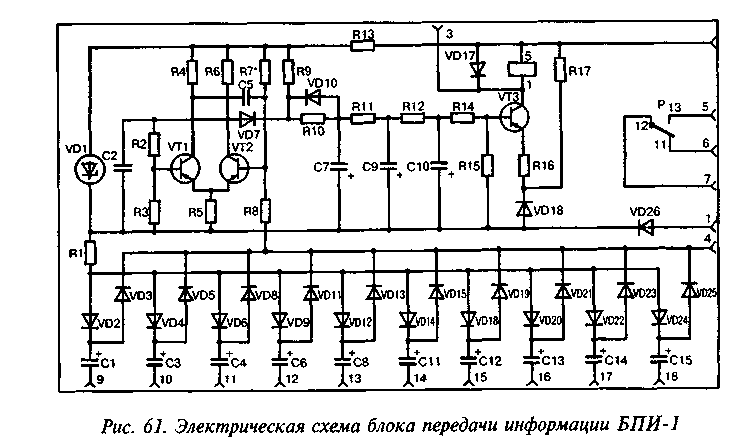

Переменные и подстроечные резисторы. Реостат.

В одной из предыдущих статей мы обсудили основные аспекты, касающиеся работы с резисторами, так вот сегодня мы продолжим эту тему. Все, что мы обсуждали ранее, касалось, в первую очередь, постоянных резисторов, сопротивление которых представляет из себя не изменяющуюся величину. Но это не единственный существующий вид резисторов, поэтому в данной статье мы уделим внимание элементам, имеющим переменное сопротивление, в частности, переменным резисторам.

Переменный резистор.

Итак, чем же отличается переменный резистор от постоянного? Собственно, здесь ответ прямо следует из названия этих элементов 🙂 Величину сопротивления переменного резистора, в отличие от постоянного, можно изменить. Каким способом? А вот это мы как раз и выясним! Для начала давайте рассмотрим условную схему переменного резистора:

Сразу же можно отметить, что тут в отличие от резисторов с постоянным сопротивлением в наличии имеется три вывода, а не два. Сейчас разберемся зачем они нужны и как все это работает…

Итак, основной частью переменного резистора является резистивный слой, имеющий определенное сопротивление. Точки 1 и 3 на рисунке являются концами резистивного слоя. Также важной частью резистора является ползунок, который может изменять свое положение (он может занять любое промежуточное положение между точками 1 и 3, например, он может оказаться в точке 2 как на схеме).

Таким образом, в итоге мы получаем следующее. Сопротивление между левым и центральным выводами резистора будет равно сопротивлению участка 1-2 резистивного слоя. Аналогично сопротивление между центральным и правым выводами будет численно равно сопротивление участка 2-3 резистивного слоя. Получается, что перемещая ползунок мы можем получить любое значение сопротивления от нуля до R_{max}. А R_{max} — это ни что иное как полное сопротивление резистивного слоя.

Конструктивно переменные резисторы бывают поворотные, то есть для изменения положения ползунка необходимо крутить специальную ручку (такая конструкция подходит для резистора, который изображен на нашей схеме). Также резистивный слой может быть выполнен в виде прямой линии, соответственно, ползунок будет перемещаться прямо. Такие устройства называют движковыми или ползунковыми перемененными резисторами. Поворотные резисторы очень часто можно встретить в аудио-аппаратуре, где они используются для регулировки громкости/баса и т. д. Вот как они выглядят:

Переменный резистор ползункового типа выглядит несколько иначе:

Часто при использовании поворотных резисторов в качестве регуляторов громкости используют резисторы с выключателем. Наверняка вы не раз сталкивались с таким регулятором — к примеру на радиоприемниках. Если резистор находится в крайнем положении (минимальная громкость/устройство выключено), то если его начать вращать, раздастся ощутимый щелчок, после которого приемник включится. А при дальнейшем вращении громкость будет увеличиваться. Аналогично и при уменьшении громкости — при приближении к крайнему положению снова будет щелчок, после которого устройство выключится. Щелчок в данном случае говорит о том, что питание приемника было включено/отключено. Выглядит такой резистор так:

Как видите, здесь есть два дополнительных вывода. Они то как раз и подключаются в цепь питания таким образом, чтобы при вращении ползунка цепь питания размыкалась и замыкалась.

Есть еще один большой класс резисторов, имеющих переменное сопротивление, которое можно изменять механически — это подстроечные резисторы. Давайте уделим немного времени и им!

Подстроечный резистор.

Только для начала уточним терминологию… По сути подстроечный резистор является переменным, ведь его сопротивление можно изменить, но давайте условимся, что при обсуждении подстроечных резисторов под переменными резисторами мы будем иметь ввиду те, которые мы уже обсудили в этой статье (поворотные, ползунковые и т. д). Это упростит изложение, поскольку мы будем противопоставлять эти типы резисторов друг другу. Да и, к слову, в литературе зачастую под подстроечными резисторами и переменными понимаются разные элементы цепи, хотя, строго говоря, любой подстроечный резистор также является и переменным в силу того факта, что его сопротивление можно изменить.

Итак, отличие подстроечных резисторов от переменных, которые мы уже обсудили, в первую очередь, заключается в количестве циклов перемещения ползунка. Если для переменных это число может составлять и 50000, и даже 100000 (то есть ручку громкости можно крутить практически сколько угодно 🙂 ), то для подстроечных резисторов эта величина намного меньше. Поэтому подстроечные резисторы чаще всего используются непосредственно на плате, где их сопротивление меняется только один раз, при настройке прибора, а при эксплуатации значение сопротивления уже не меняется. Внешне подстроечный резистор выглядит совсем не так как упомянутые переменные:

Из-за небольшой износоустойчивости не рекомендуется применять подстроечные резисторы вместо переменных — в цепях, в которых регулировка сопротивления будет производиться довольно часто.

Обозначение переменных резисторов немного отличается от обозначения постоянных:

Собственно, мы обсудили все основные моменты, касающиеся переменных и подстроечных резисторов, но есть еще один очень важный момент, который невозможно обойти стороной.

Часто в литературе или в различных статьях вы можете встретить термины потенциометр и реостат. В некоторых источниках так называют переменные резисторы, в других в эти термины может вкладываться какой-нибудь иной смысл. На самом деле, корректная трактовка терминов потенциометр и реостат есть только одна. Если все термины, которые мы уже упоминали в этой статье относились,в первую очередь, к конструктивному исполнению переменных резисторов, то потенциометр и реостат — это разные схемы включения (!) переменных резисторов. То есть, к примеру, поворотный переменный резистор может выступать и в роли потенциометра и в роли реостата — все зависит от схемы включения. Начнем с реостата.

Реостат.

Реостат (переменный резистор, включенный по схеме реостата) в основном используется для регулировки силы тока. Если мы включим последовательно с реостатом амперметр, то при перемещении ползунка будем видеть меняющееся значение силы тока. Резистор R_1 в этой схеме исполняет роль нагрузки, ток через которую мы и собираемся регулировать переменным резистором. Пусть максимальное сопротивление реостата равно R_{max}, тогда по закону Ома максимальный ток через нагрузку будет равен:

I = \frac{U}{R_1 + 0}

Здесь мы учли то, что ток будет максимальным при минимальном значении сопротивления в цепи, то есть когда ползунок в крайнем левом положении. Минимальный ток будет равен:

I = \frac{U}{R_1 + R_{max}}

Вот и получается, что реостат выполняет роль регулировщика тока, протекающего через нагрузку. В данной схеме есть одна проблема — при потере контакта между ползунком и резистивным слоем цепь окажется разомкнутой и через нее перестанет протекать ток. Решить эту проблему можно следующим образом:

Отличие от предыдущей схемы заключается в том, что дополнительно соединены точки 1 и 2. Что это дает в обычном режиме работы? Да ничего, никаких изменений 🙂 Поскольку между ползунком резистора и точкой 1 ненулевое сопротивление, то весь ток потечет напрямую на ползунок, как и при отсутствии контакта между точками 1 и 2. А что же произойдет при потере контакта между ползунком и резистивным слоем? А эта ситуация абсолютно идентична отсутствию прямого соединения ползунка с точкой 2. Тогда ток потечет через реостат (от точки 1 к точке 3), и величина его будет равна:

I = \frac{U}{R_1 + R_{max}}

То есть при потере контакта в данной схеме будет всего лишь уменьшение силы тока, а не полный разрыв цепи как в предыдущем случае.

С реостатом мы разобрались, давайте рассмотрим переменный резистор, включенный по схеме потенциометра.

Потенциометр.

Не пропустите статью про измерительные приборы в электрических цепях — ссылка.

Потенциометр, в отличие от реостата, используется для регулировки напряжения. Именно по этой причине на нашей схеме вы видите целых два вольтметра! Ток протекающий через потенциометр, от точки 3 к точке 1, при перемещении ползунка остается неизменным, но меняется величины сопротивления между точками 2-3 и 2-1. А поскольку напряжение прямо пропорционально силе тока и сопротивлению, то оно будет меняться.

При перемещении ползунка вниз сопротивление 2-1 будет уменьшаться, соответственно, уменьшаться будут и показания вольтметра 2. А сопротивление участка 2-3 вырастет, а вместе с ним и напряжение на вольтметре 1. При этом в сумме показания вольтметров будут равны напряжению источника питания, то есть 12 В. В крайнем верхнем положении на вольтметре 1 будет 0 В, а на вольтметре 2 — 12 В. На рисунке ползунок расположен в среднем положении, и показания вольтметров, что абсолютно логично, равны 🙂

На этом мы заканчиваем рассматривать переменные резисторы, в следующей статье речь пойдет о возможных соединениях резисторов между собой, спасибо за внимание, рад буду видеть вас на нашем сайте! 🙂

Резисторы переменные, постоянные вся истина!

Друзья, всем привет! На дворе зима а календарь говорит мне, что будни перетекают в приятные праздничные выходные, так что самое время для новой статьи.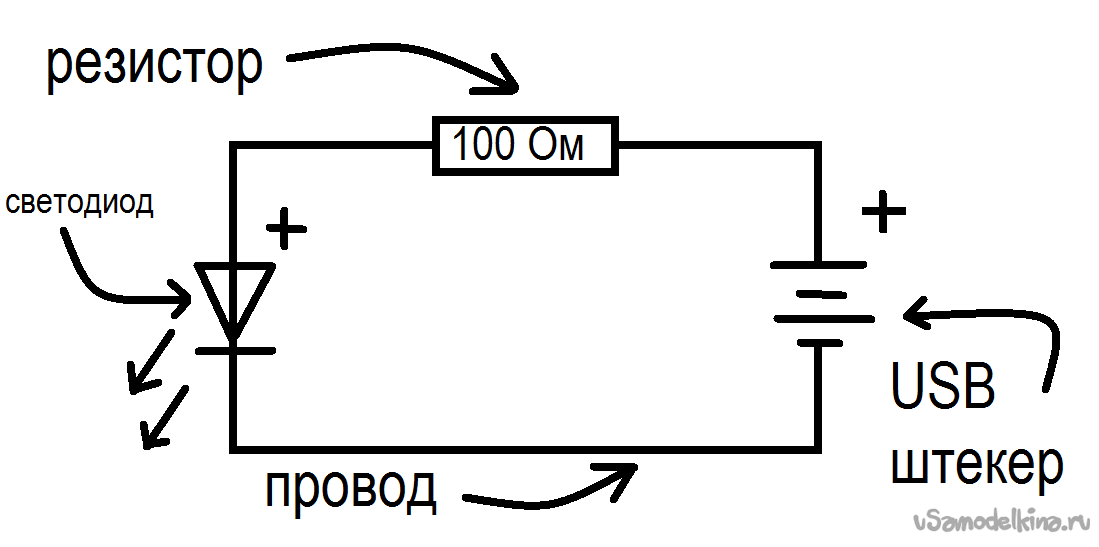 Для тех кто меня не знает, скажу, что меня зовут Владимир Васильев и я веду вот этот самый радиолюбительский блог, так что добро пожаловать!

В прошлой статье мы разбирались с понятием электрического тока и напряжения. В ней буквально на пальцах я постарался объяснить что представляет собой электричество. В помощь применял некие «сантехнические аналогии».

Боле того, я наметил для себя написать ряд обучающих статей для совсем начинающих радиолюбителей- электронщиков, так что дальше будет больше — [urlspan]не пропустите.[/urlspan]

Содержание статьи

Сегодняшняя статья будет не исключением, сегодня я постараюсь как можно подробнее осветить тему резисторов. Резисторы хоть и являются, наверно самыми простыми радиокомпонентами, но у начинающих могут вызвать массу вопросов. А отсутствие ответов на них может привести к полному бардаку в голове и привести к отсутствию мотивации и желанию развиваться.

Что такое сопротивление?

Резистор — это пассивный элемент электрической цепи, обладающий фиксированным или переменным значением электрического сопротивления.

Резисторы обладают сопротивление, а что такое сопротивление? Постараемся с этим разобраться.

Чтобы ответить на этот вопрос, давайте вернемся снова к нашей сантехнической аналогии. Под действием силы тяжести или под действием давления насоса, вода устремляется от точки большего давления в точку с меньшим давлением. Так и электрический ток под действием напряжения течет из точки большего потенциала в точку с меньшим потенциалом.

Что может помешать движению воды по трубам? Движению воды может помешать состояние труб, по которым она бежит. Трубы могут быть широкими и чистыми, а могут быть загажены и вообще представлять собой печальное зрелище. В каком случае скорость водного потока будет больше? Естественно, что вода будет течь быстрее если ее движению не будет оказываться никакого сопротивления.

В случае с чистым трубопроводом так и будет, воде будет оказываться наименьшее сопротивление и ее скорость будет практически неизменной. В загаженной трубе сопротивление на водный поток будет значительным, и соответственно скорость движения воды будет не очень.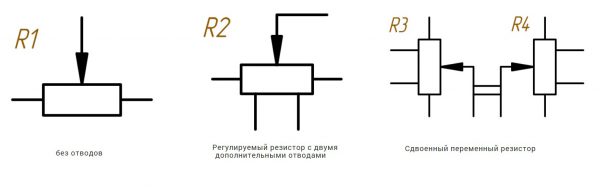

Хорошо, теперь переносимся из нашей водопроводной модели в реальный мир электричества. Теперь становится понятно, что скорость воды в наших реалиях представляет собой силу тока измеряемую в амперах. Сопротивление которое оказывали трубы на воду, в реальной токоведущей системе будет сопротивление проводов измеряемое в омах.

Как и трубы, провода могут оказывать сопротивление на ток. Сопротивление напрямую зависит от материала из которого сделаны провода. Поэтому совсем не случайно провода часто изготавливают из меди, так как медь имеет небольшое сопротивление.

Другие металлы могут оказывать очень большое сопротивление электрическому току. Так для примера, удельное сопротивление (Ом*мм²) нихрома составляет 1.1Ом*мм². Величину сопротивления нетрудно оценить сравнив с медью у которой удельное сопротивление 0,0175Ом*мм². Неплохо да?

При пропускании тока через материал с высоким сопротивлением, мы можем убедиться, что ток в цепи будет меньше, достаточно провести несложные замеры.

Как выглядит резистор?

В природе встречаются абсолютно различные резисторы. Есть резисторы с постоянным сопротивление, есть резисторы с переменным сопротивлением. И каждый вид резисторов находит свое применение. Так давайте остановимся и постараемся уделить вниманием некоторые из них.

Постоянные резисторы.

Само название говорит о том, что они обладают постоянным фиксированным сопротивлением. Каждый такой резистор изготавливается с определенным сопротивлением, определенной рассеиваемой мощностью.

Рассеиваемая мощность — это еще одна характеристика резисторов, так же как и сопротивление. Мощность рассеяний говорит о том, какую мощность может рассеять резистор в виде тепла (вы наверное замечали, что резистор во время работы может значительно нагреваться).

Естественно, что на заводе не могут изготавливать резисторы абсолютно любые. Поэтому постоянные резисторы имеют определенную точность указываемую в процентах. Эта величина показывает в каких пределах будет гулять результирующее сопротивление.И естественно, чем точнее резистор, тем дороже он будет. Так зачем переплачивать?

Также сама величина сопротивления не может быть любой. Обычно сопротивление постоянных резисторов соответствует определенному номинальному ряду сопротивлений. Эти сопротивления обычно выбираются из рядов типо Е3, Е6, Е12,Е24

Как видите резисторы из ряда Е24 имеют более богатый набор сопротивлений. Но это еще не предел так как существуют номинальные ряды E48, E96, E192.

На электрических схемах постоянные резисторы обозначаются эдаким прямоугольником с выводами. На самом условном графическом обозначении может надписываться мощность рассеяния.

Переменные резисторы

Вы когда-нибудь обращали внимание на различные «крутилки» в старой аналоговой технике. Например, задумывались ли о том что вы крутите, прибавляя громкость в старом, возможно даже ламповом телевизоре?

Многие регуляторы и различные «крутилки»представляют собой переменные резисторы.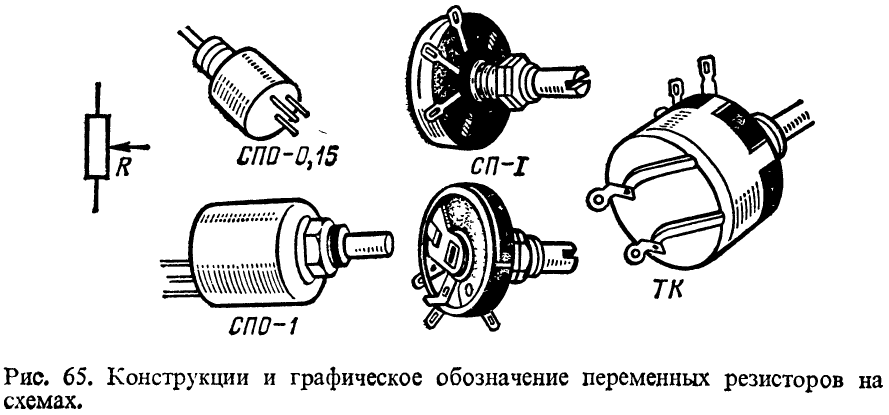 Так же как и постоянные резисторы, переменные также имеют различную рассеивающую мощность. Однако их сопротивление может меняться в широких пределах.

Переменные резисторы служат для регулирования напряжения или тока в уже готовом изделии. Как я уже упоминал этим резистором может регулироваться сопротивление в схеме формирования звука. Тогда громкость звука будет меняться пропорционально углу поворота ручки резистора. Так сам корпус находится внутри устройства, а та самая крутилка остается на поверхности.

Более того, бывают еще и сдвоенные , строенные , счетверенные и так далее переменные резисторы. Обычно их применяют, когда нужно параллельное изменение сопротивления сразу в нескольких участках схемы.

Условное графическое изображение резистора на электрических схемах.

Подстроечные резисторы.

Переменный резистор это очень хорошо, но что если нам нужно изменение или подстройка сопротивления лишь на этапе сборки изделия?

Переменный резистор нам в этом не очень подходит.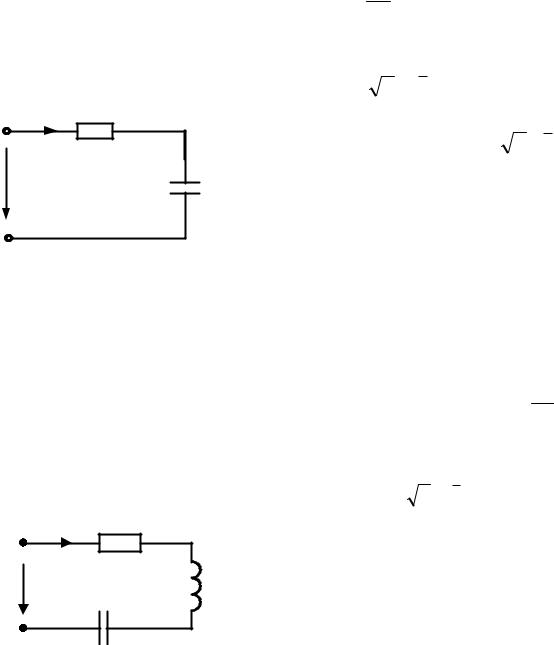 Переменный резистор обладает меньшей точностью нежели постоянный. Это плата за возможность регулировки, в результате которой сопротивление может гулять в некоторых пределах.

Конечно на этапе налаживания изделия может применяться так называемый подборочный резистор. Это обычный постоянный резистор, только при монтаже он подбирается из кучки резисторов с близкими номиналами.

Подбор резисторов имеет место быть когда требуется регулировка параметров изделия и при этом требуется высокая точность работы (чтобы требуемый параметр как можно меньше плавал). Таким образом нужно чтобы резистор был как можно большей точностью 1% или даже 0,5%.

Так для подстройки параметров схемы чаще всего применяют подстроечные резисторы. Эти резисторы специально придуманы для этих целей. Подстройка осуществляется посредством тоненькой часовой отвертки, причем после достижения требуемой величины сопротивления ползунок резистора часто фиксируют краской или клеем.

Условное графическое изображение подстроечного резистора

Формулы и свойства

При выборе резистора, помимо его конструктивной особенности, следует обращать внимания на основные его характеристики. А основными его характеристиками, как я уже упоминал, являются сопротивление и мощность рассеяния.

Между этими двумя характеристиками есть взаимосвязь. Что это значит? Вот допустим в схеме у нас стоит резистор с определенной величиной сопротивления. Но по каким-либо причинам мы выясняем, что сопротивление резистора должно быть значительно меньше того, что есть сейчас.

И вот что получается, мы ставим резистор с значительно меньшим сопротивлением и в соответствии с законом Ома мы можем получить небольшое западло.

Так как сопротивление резистора было большим, а напряжение в цепи у нас фиксированное, то вот что получилось. При уменьшении номинала резистора общее сопротивление в цепи упало, следовательно ток в проводах возрос.

Но что если мы поставили резистор с прежней мощностью рассеяния? При возросшем токе , новый резистор может и не выдержать нагрузки и умереть, его душа улетит вместе с клубком дыма из бездыханного тельца резистора 🙂

Выходит, что при номинале резистора 10 Ом, в цепи будет течь ток равный 1 А. Мощность которая будет рассеиваться на резисторе будет равняться

Видите какие грабли могут подстерегать на пути. Поэтому при выборе резистора, обязательно нужно смотреть его допустимую мощность рассеяния.

Последовательное соединение резисторов

А давайте теперь посмотрим как будут меняться свойства цепи при последовательном расположении резисторов. Итак у нас есть источник питания и далее стоят последовательно три резистора с различным сопротивлением.

Попробуем определить какой ток протекает в цепи.

Здесь хочется упомянуть, для тех кто не в теме, что электрический ток в цепи только один. Есть правило Кирхгофа, которое гласит что сумма токов втекающих в узел равно сумме токов вытекающих из узла. А так как в данной схеме у нас последовательное расположение резисторов и никаких узлов и в помине нет , то ясно, что ток будет один.

Для определения тока, нам нужно определить полное сопротивление цепи. Находим сумму всех резисторов показанных на схеме.

Здесь я приведу формулу полного сопротивления при последовательном расположении резисторов.

Полное сопротивление получилось равным 1101 Ом. Теперь зная что полное напряжение (напряжение источника питания)равно 10 В, а полное сопротивление равно 1101 Ом, тогда ток в цепи равняется I=U/R=10В/1101 Ом=0,009 А =9 мА

Зная ток мы можем определить напряжение, высаживаемое на каждом резисторе. Для этого также воспользуемся законом Ома. И получается напряжение на резисторе R1 будет равно U1=I*R1=0.009А*1000Ом=9В. Ну и тогда для остальных резисторов U2=0.9В, U3=0.09В. Теперь можно и проверить сложив все эти напряжения, ну и получив в результате значенье близкое напряжению питания.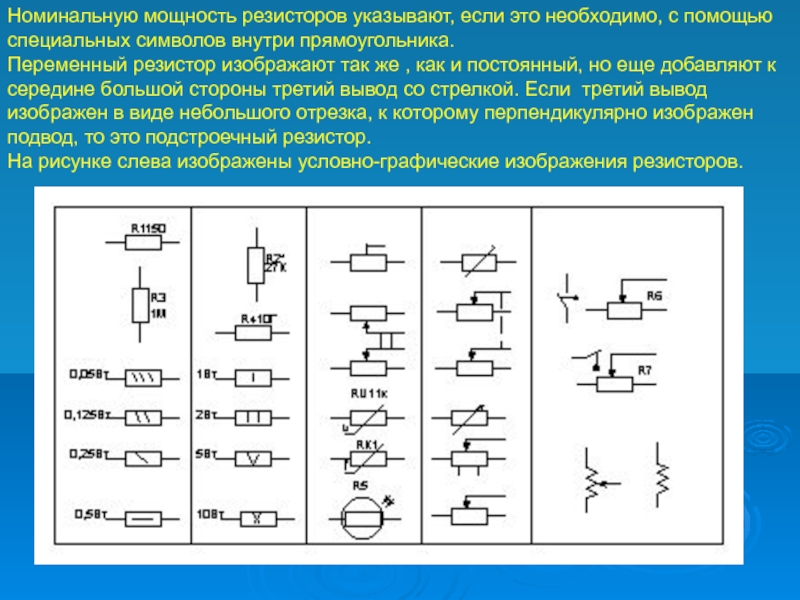

Ах да вот вам и делитель напряжения. Если сделать отвод после каждого резистора то можно убедиться в наличии еще некоторого набора напряжений. Если при этом использовать равные сопротивления то эффект делителя напряжения будет еще более очевиден.

Кликните для увеличения

На изображении видно как меняется напряжение между разными точками -потенциалами.

Так как резисторы сами по себе являются хорошими потребителями тока, то понятно, что при использовании делителя напряжения, стоит выбирать резисторы с минимальными сопротивлениями. Кстати мощность расходуемая на каждом резисторе будет одинаковой.

Для резистора R1 мощность будет равняться P=I*R1=3.33A*3.33В=11,0889Вт. Округляем и получаем 11Вт. И каждый резистор естественно должен быть на это рассчитан. Потребляемая мощность всей цепи будет P=I*U=3.33A*10В=33,3Вт.

Сейчас я вам покажу какая мощность будет для резисторов имеющих разное сопротивление.

Кликните для увеличения

Мощность потребляемая всей цепочкой, изображенной на рисунке, будет равняться P=I*U=0. 09A*10В=0,9Вт.

Теперь рассчитаем мощность потребляемую каждым резистором:
Для резистора R1: P=I*U=0.09A*0.9В=0,081Вт;

Для резистора R2: P=I*U=0.09A*0.09В=0,0081Вт;

Для резистора R3: P=I*U=0.09A*9В=0,81Вт.

Из этих наших расчетов становится понятной закономерность:

Чем больше общее сопротивление цепочки резисторов, тем меньше будет ток в цепи
Чем больше сопротивление конкретного резистора в цепи, тем большая мощность будет на нем выделяться и тем больше он будет греться.

Поэтому становится понятной необходимость подбирать номиналы резисторов в соответствии с их потребляемой мощностью.

Параллельное соединение резисторов

С последовательным расположение резисторов думаю более менее понятно. Так давайте рассмотрим параллельное соединение резисторов.

Здесь на этом изображении схемы показано различное расположение резисторов. Хотя в заголовке я упомянул о параллельном соединении, думаю наличие последовательно соединенного резистора R1 позволит нам разобраться в некоторых тонкостях.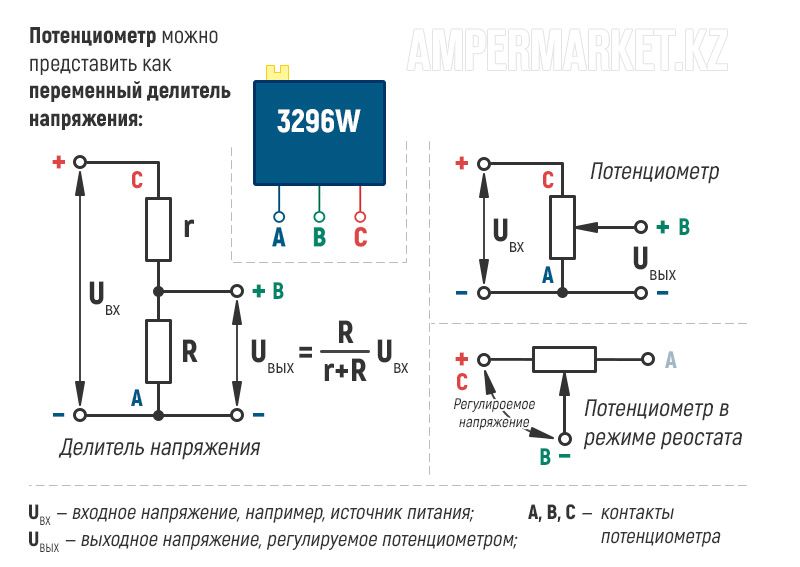

Итак суть заключается в том что последовательная схема соединения резисторов является делителем напряжения, а вот параллельное соединение представляет собой делитель тока.

Рассмотрим это подробнее.

Ток течет от точки с большим потенциалом к точке с меньшим потенциалом. Естественно, что ток из точки с потенциалом 10В стремится к точке нулевого потенциала — земле. Маршрут тока будет : Точка10В —>>точка А—>>точка В—>>Земля.

На участке пути Точка 10 —Точка А, ток будет максимальным, ну просто потому, что ток бежит по прямой и не разделяется на развилках.

Далее по правилу Кирхгофа, ток будет раздваиваться. Получается ток в цепи резисторов R2 и R4 будет одним а в цепи с резистором R3 другим. Сумма токов этих двух участков будет равняться току на самом первом отрезке (от источника питания до точки А).

Давайте рассчитаем эту схему и узнаем значение тока на каждом участке.

Для начала узнаем сопротивление участка цепи резисторов R2, R4

Значение резистора R3 нам известен и равен 100Ом.

Теперь находим сопротивления участка АВ. Сопротивление цепи резисторов, соединенных параллельно будет вычислено по формуле:

Ага, подставили в формулу наши значения для суммы резисторов R2 и R4 (Сумма равна 30 Ом и подставляется вместо формульной R1) и значение резистора R3 равное 100 Ом (Подставляется вместо формульной R2). Вычисленное значение сопротивления на участке АВ равняется 23 Ом.

Как видите выполнив несложные вычисления наша схема упростилась и свернулась и стала нам уже более знакомой.

Ну и полное сопротивление цепи будет равняться R=R1+R2=23Ом+1Ом=24Ом. Это мы нашли уже по формуле для последовательного соединения. Мы это рассматривали так что на этом останавливаться не будем.

Теперь ток на участке до разветвлений (участок Точка 10В —>>Точка А) мы сможем найти по формуле Ома.

I=U/R=10В/24Ом=0,42A . Получилось 0,42 ампера. Как мы уже обсуждали этот ток будет один на всем пути от точки максимального потенциала, до точки А. На участке А В, значение тока будет равно сумме токов с участков полученных после разделения.

Чтобы определить ток на каждом участке между точками А и В, нам нужно найти напряжение между точками А и В.

Оно как уже известно будет меньше напряжения питания 10В. Его мы найдем по формуле U=I*R=0.42A*23Ом=9,66В.

Как вы могли заметить полный ток в точе А (равный сумме токов параллельных участков) умножается на результирующее сопротивление запараллеленных (сопротивление резистора R1 мы не учитываем) участков цепи.

Теперь мы можем найти ток в цепи резисторов R2, R4. Для этого напряжение между точками А и В разделим на сумму этих двух резисторов. I=U/(R2+R4)=9.66В/ 30Ом=0,322А.

Ток в цепи резистора R3 тоже найти не сложно. I=U/R3=9.66В/100Ом=0,097А.

Как видите при параллельно соединении резисторов ток делится пропорционально значениям сопротивлений. Чем больше сопротивление резистора, тем меньше будет ток на этом участке цепи.
В тоже время напряжение между точками А и В, будет относиться к каждому из параллельных участков (напряжение U=9. 66В мы использовали для расчетов и там и там ).
Здесь хочется сказать как напряжение и ток распределяются по схеме.
Как я уже говорил ток до разветвления равен сумме токов после развилки. Впрочем умный мужик Кирхгоф нам это уже рассказывал.
Получается следующее: Ток I на развилке разделится на три I1, I2, I3, а затем снова воссоединится в I как было и в самом начале, получаем I=I1+I2+I3.
Для напряжения или разности потенциалов, что есть одно и тоже будет следующее. Разность потенциалов между точками А и С (далее буду говорить напряжение AC), не равна напряжениям BE, CF,DG. В тоже время напряжения BE, CF,DG , будут равны между собой. Напряжение на участке FH вообще равно нулю, так как напряжению просто не на чем высаживаться (нет резисторов).

Думаю тему параллельного соединения резисторов я раскрыл, но если есть еще какие-то вопросы то пишите в комментариях, чем смогу помогу 🙂

Преобразование звезды в треугольник и обратно

Существуют схемы, в которых резисторы соединены так, что не совсем понятно где есть последовательное соединение а где параллельное.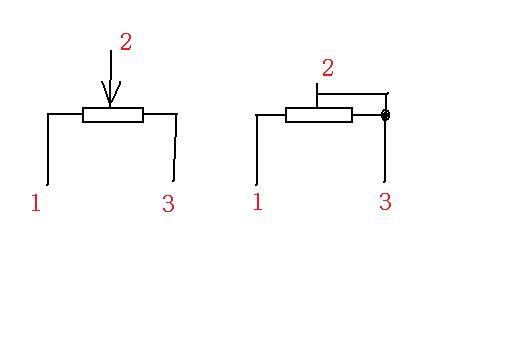 И как же с этим быть?

Для этих ситуаций есть способы упрощения схем и вот одни из них это преобразование треугольника в эквивалентную звезду или наоборот, если это необходимо.

Для преобразования треугольника в звезду считать будем по формулам:

Для того чтобы совершить обратное преобразование нужно воспользоваться несколько другими формулами:

С вашего позволения я не буду приводить конкретные примеры, все что требуется это только подставить в формулы конкретные значения и получить результат.

Этот метод эквивалентного преобразования будет служить хорошим подспорьем в мутных случаях, когда не совсем понятно с какой стороны подступиться к схеме. А тут порой поменяв звезду на треугольник ситуация проясняется и становится более знакомой.

Ну чтож дорогие друзья вот и все, что я хотел вам сегодня рассказать. Мне кажется эта информация будет полезной для вас и принесет свои плоды.

Хочу еще добавить, что многое из того что я здесь выложил очень хорошо расписано в книгах «Искусство схемотехники» и «Занимательная микроэлектроника», так что рекомендую прочитать обзорные статьи и скачать себе эти книжки. А будет еще лучше, если вы их раздобудете где-нибудь в бумажном варианте.

P.S. У меня на днях возникла одна идея о том как можно получить интересный способ заработка на знаниях электроники и вообще радиолюбительском хобби так что обязательно [urlspan]подпишитесь на обновления.[/urlspan]

Кроме того относительно недавно появился еще один прогрессивный способ подписки через форму сервиса Email рассылок, так что люди подписываются и получают некие приятные бонусы, так что добро пожаловать.

А на этом у меня действительно все, я желаю вам успехов во всем , прекрасного настроения и до новых встреч.

С н/п Владимир Васильев.

Конструктор ЗНАТОК 320-Znat «320 схем»

Конструктор ЗНАТОК 320-Znat «320 схем» — это инструмент, который позволит получить знания в области электроники и электротехники а также достичь понимания процессов происходящих в проводниках.

Конструктор представляет собой набор полноценных радиодеталей имеющих спец. конструктив, позволяющий их монтаж без помощи паяльника. Радиокомпоненты монтируются на специальную плату — основание, что позволяет в конечном итоге получить вполне функциональные радиоконструкции.

Используя этот конструктор можно собрать до 320 различных схем, для построения которых есть развернутое и красочное руководство. А если подключить фантазию в этот творческий процесс то можно получить бесчисленное количество различных радиоконструкций и научиться анализировать их работу. Этот опыт я считаю очень важен и для многих он может оказаться бесценным.

Вот несколько примеров того, что Вы можете сделать благодаря этому конструктору:

Летающий пропеллер;
Лампа,включаемая хлопком в ладоши или струей воздуха;
Управляемые звуки звездных войн, пожарной машины или скорой помощи;
Музыкальный вентилятор;
Электрическое световое ружье;
Изучение азбуки Морзе;
Детектор лжи;
Автоматический уличный фонарь;
Мегафон;
Радиостанция;
Электронный метроном;
Радиоприемники, в том числе FM диапазона;
Устройство, напоминающее о наступлении темноты или рассвета;
Сигнализация о том, что ребенок мокрый;
Защитная сигнализация;
Музыкальный дверной замок;
Лампы при параллельном и последовательном соединении;
Резистор как ограничитель тока;
Заряд и разряд конденсатора;
Тестер электропроводимости;
Усилительный эффект транзистора;
Схема Дарлингтона.

Как выбрать подходящий резистор

Все, что вам нужно знать о том, как правильно выбрать резистор для вашего первого проекта печатной платы

Вы планируете приступить к вашему первому проекту печатной платы? Есть множество радиодеталей, которые вы в конечном итоге будете использовать. Однако нет другой такой детали, которая была бы так печально известна, как простой резистор. Если вы когда-либо видели печатную плату, то могли заметить резисторы по всей ее поверхности. Они контролируют силу тока и заставляют светиться светодиоды. Но что именно представляет собой резистор? Как он работает? Как вообще выбрать подходящий резистор для вашего первого проекта печатной платы? Не бойтесь, мы поможем вам и подскажем все необходимое, что вам нужно знать.

Итак… что такое резистор?

Резисторы – это одни из множества пассивных компонентов. Их задача относительно проста, но очень важна – создавать сопротивление току в электрической цепи. Видели, как загорается светодиод? За эту возможность необходимо поблагодарить резистор. Устанавливая в электрическую цепь резистор последовательно со светодиодом, вы получаете яркое свечение, при этом ничего не перегорает!

Основной характеристикой резистора является сопротивление, измеряемое в Омах (Ом). Если раньше вы прослушали базовый курс электроники, то, скорее всего, изучили закон Ома. При работе с резисторами вы будете вновь и вновь иметь с ними дело.

Закон Ома – это единственная формула для нахождения сопротивления

Найти обозначение резистора на схеме легко. Международное обозначение – стандартизированный прямоугольник, но в стандартах США резистор обозначается зигзагообразной линией – это сделано для простоты его нахождения. Вне зависимости от внешнего вида символа, каждый резистор на концах имеет выводы, обозначенные на схеме.

Обозначения резистора на схемах, принятое в США (слева) и соответствующее международным стандартам (справа). На схемах можно встретить оба обозначения.

Какие бывают резисторы?

Повсеместно встречаются резисторы совершенно разных конструкций. Все резисторы можно разделить на две категории по типу конструкции и по резистивному материалу. Рассмотрим обе категории.

Тип конструкции

Постоянные резисторы – как следует из названия, эти резисторы имеют постоянное сопротивление и точность, не зависящие от изменения температуры, освещенности и так далее.

Переменные резисторы – эти радиоэлементы обладают переменным сопротивлением. Потенциометр – великолепный пример такого резистора. У него есть регулятор, который можно вращать для увеличения или уменьшения сопротивления. Другие разновидности переменных резисторов – это подстроечный резистор и реостат.

Нелинейные резисторы – эти резисторы как хамелеоны, они могут изменять свое сопротивление в зависимости от той или иной физической величины, воздействующей на резистор – температуры, уровня освещенности и даже магнитного поля. Нелинейные резисторы – это термистор, фоторезистор, варистор и магниторезистор.

Резистивный материал

Все резисторы можно разбить на группы по материалам, из которых они изготовлены и которые в огромной степени влияют на их способность оказывать сопротивление электрическому току. Вот эти резисторы по используемым материалам:

Углеродистые композиционные резисторы;
Углеродистые пленочные резисторы;
Металлопленочные резисторы;
Тонко и толстопленочные резисторы;
Фольговые резисторы;
Проволочные резисторы.

Углеродистые композиционные резисторы – это резисторы, изготовленные по самой старой технологии, популярной в производстве резисторов малой точности. Их все еще можно найти в схемах, где могут быть импульсы высоких энергий.

Старый углеродистый пленочный резистор.

Такие резисторы все еще используются там, где точность не важна

Из всех вышеперечисленных типов резисторов по резистивному материалу старейшими являются проволочные резисторы. Их все еще можно встретить на старых печатных платах устройств большой мощности, в которых необходимо сопротивление, заданное с большой точностью. Эти древние резисторы широко известны благодаря тому, что большой надежностью обладают даже резисторы с малым сопротивлением.

Проволочный резистор – старейший и наиболее точный из доступных резисторов

Сегодня наиболее широко применяются металлопленочные и металлооксидные резисторы, они лучше всего обеспечивают с неизменной точностью номинальное сопротивление, а также меньше подвержены влиянию изменения температуры.

Наиболее широко применяемый металлооксидный резистор

обеспечивает неизменную точность номинального сопротивления

Как используются резисторы?

Можно найти резисторы, используемые самыми различными способами. Они применяются не только для того, чтобы оказывать сопротивление электрическому току. Резисторы используются в делителях напряжения, для производства тепла, в цепях сопряжения и нагрузки, для управления усилением и для настройки постоянных времени. Практическое применение резисторов можно найти в цепях питания электрических тормозов поездов, здесь они помогают высвобождению всей накопленной кинетической энергии.

Серьезное сопротивление – взгляните на тормоза у этого поезда,

которые высвобождают накопленную кинетическую энергию

Вот еще несколько замечательных устройств, в которых используются эти универсальные резисторы:

Измерение величины электрического тока – вы можете измерять падение напряжения на включенном в цепь прецизионном резисторе с заранее известным сопротивлением. Расчет тока производится по закону Ома;
Питание светодиодов – слишком большой ток, протекающий через светодиод, сожжет этот прекрасный фонарик. Соединив последовательно со светодиодом резистор, вы можете контролировать силу тока через светодиод, обеспечивая его яркое сияние.
Питание электромоторов вентиляторов – сердцем системы автомобильной вентиляции является электромотор вентилятора печки. Специальный датчик используется для управления скоростью вращения крыльчатки вентилятора. Резистор такого типа, используемый в датчике, называется, (кто бы мог подумать!) резистором мотора вентилятора!

Резистор мотора вентилятора в ответе за движение воздуха в машине

Как измеряется номинал резистора?

Эта характеристика, с которой вы будете сталкиваться снова и снова, называется сопротивлением. Величина сопротивления наносится на резистор различными способами. В настоящее время существуют два стандарта нанесения значения сопротивления резистора на корпус резистора – это цветовая маркировка или маркировка SMD-резисторов.

Цветовая маркировка

Возможно, вы уже сталкивались с системой цветовой маркировки, если когда-либо возились с макетом электронной схемы. Эта техника была изобретена в 20-х годах прошлого века. Значения величины сопротивления и точности резистора отображалась при помощи нескольких цветных полос, нанесенных на корпус резистора.

Обратите внимание, что цветные полосы на резисторах различаются,

обозначая их уникальные номинальные значения сопротивления и точности.

Большинство резисторов, которые могут попасть к вам в руки, будет иметь четыре цветные полосы. Вот как следует их читать:

Первые две полосы указывают первые цифры номинального значения сопротивления;
Третья полоса указывает множитель, на который следует умножить число, состоящее из двух цифр, указанных первыми двумя полосами.
И, наконец, четвертая полоса указывает точность резистора. Точность очень сильно влияет на стоимость используемого резистора и на цену готового изделия. Поэтому чтобы сэкономить деньги на производстве печатных плат, точность резисторов следует выбирать разумно.

Каждый цвет на резисторе соответствует определенному числу. Вы можете воспользоваться удобным калькулятором номинала резистора по его цветовому коду для быстрого определения номинала в будущем.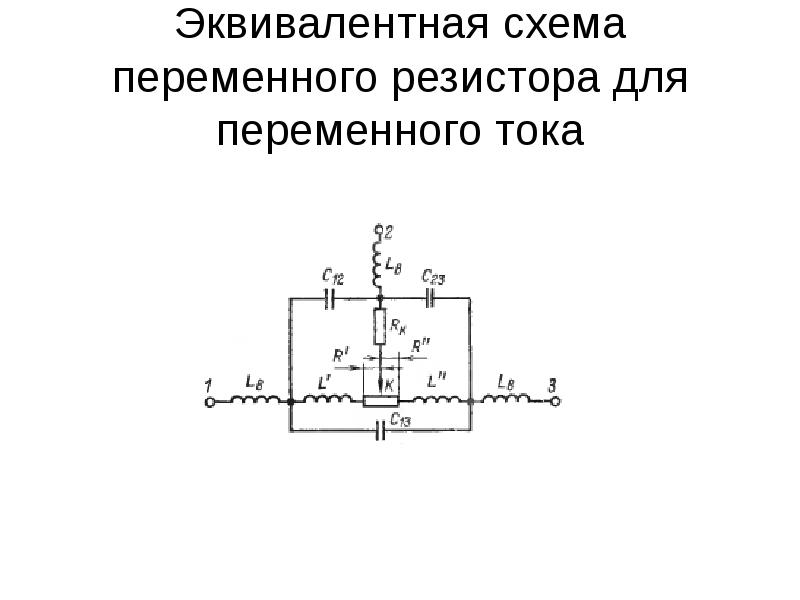 Если вам легче запомнить наглядную информацию, то ниже мы приводим великолепное видео, в котором рассказано о принципе цветовой маркировки резисторов.

Резисторы для поверхностного монтажа – SMD-резисторы

Не у всех резисторов размеры позволяют нанести на него цветовую маркировку. Это особенно актуально, когда речь идет о радиоэлементах для поверхностного монтажа (SMD). Чтобы маркировка смогла поместиться на небольшой поверхности устройства, SMD-резисторы имеют цифровую маркировку. Если вы посмотрите на современную печатную плату, то заметите, что SMD-резисторы еще имеют одинаковые размеры. Это помогает стандартизировать процесс производства с использованием высокоскоростных автоматов размещения деталей.

Как читать номинал на верхней стороне SMD-резисторов

Как выбрать подходящий резистор

Итак, пришло время наиболее важной части нашей статьи. Давайте узнаем, как определить, какой именно резистор нам нужен для вашего первого проекта печатной платы. Мы разобьем эту задачу на следующие три шага:

Расчет требуемого сопротивления;
Расчет номинальной мощности;
И, наконец, выбор резистора исходя из двух значений найденных ранее.

Шаг 1 – Расчет требуемого сопротивления

Именно здесь для расчета требуемого сопротивления нам понадобится закон Ома. Вы можете воспользоваться одной из стандартных формул ниже, если значения напряжения и силы тока известны.

Шаг 2 – Расчет номинальной мощности

Теперь необходимо выяснить, какое количество энергии должен будет рассеивать резистор. Эту величину можно рассчитать по следующей формуле:

В данной формуле P – мощность рассеивания в Ваттах, V – падение напряжения на резисторе в Вольтах, а R – сопротивление резистора в Омах. Ниже мы привели краткий пример использования данной формулы для расчета в конкретной цепи.

Простая цепь для демонстрации расчета номинальной мощности

Цепь выше содержит светодиод, падение напряжения на котором составляет 2 В, резистор с сопротивлением 350 Ом и источник питания 9 В.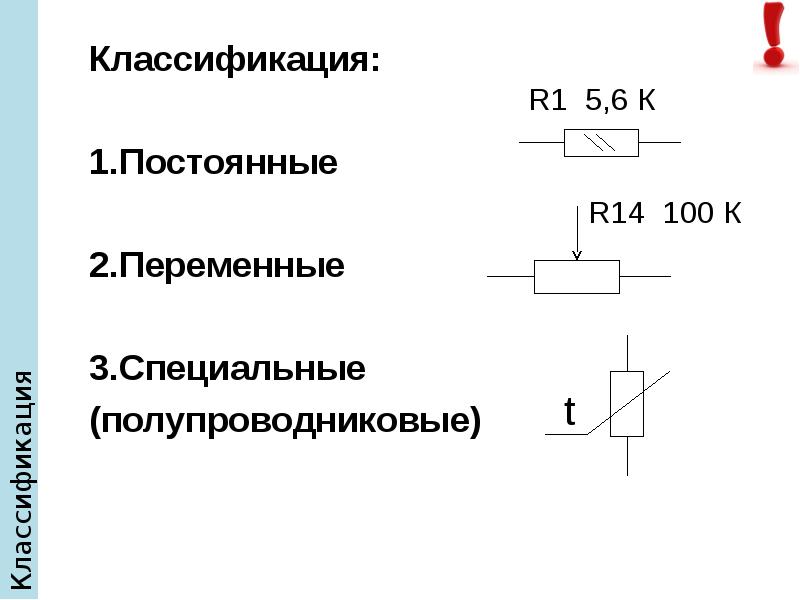 Какая мощность будет рассеиваться на искомом резисторе? Давайте посмотрим. Сначала нам необходимо найти падение напряжения на резисторе. Поскольку источник питания дает 9 В, а на светодиоде падает 2 В, то получим:

9 В – 2 В = 7 В

Эти значения можно подставить в формулу:

P = 7 В * 7 В / 350 Ом = 0,14 Ватта

Шаг 3 – Выбор резистора

Теперь, когда у нас есть величины сопротивления и мощности, пора подобрать подходящий радиоэлемент у поставщика радиодеталей. Мы всегда рекомендуем выбирать из стандартных резисторов, которые поставляются в продажу каждым продавцом. Выбирая стандартные резисторы, вы значительно упростите себе жизнь, когда дело дойдет до производства устройства. В США тремя ведущими поставщиками радиоэлементов, качество которых не вызывает сомнений – это Digikey, Mouser и Farnell/Newark.

Сопротивление сильно

Теперь мы охватили всю информацию о резисторах, которая может вам понадобиться для вашего первого проекта печатной платы. Резисторы настолько многофункциональны, что вы увидите, как раз за разом используете их россыпи в своих электронных устройствах. В следующий раз, когда вам понадобиться выбрать резистор, вспомните три простых шага – рассчитайте сопротивление, найдите мощность и выберите поставщика!

Прежде чем вы броситесь размечать обозначения резисторов и их корпусов в вашем приложении для конструирования печатных плат, не было бы проще, если бы кто-то сделал это за вас? Уже сделали! Для многих систем проектирования печатных плат существует большое количество бесплатных библиотек радиоэлементов. И резисторы там тоже есть!

Резисторы

в схемах – Резюме – Гипертекст по физике

Резисторы в схемах – Резюме – Гипертекст по физике

Сводка

Основными компонентами простой схемы являются…
- источник напряжения или разности потенциалов ( В, ), например аккумулятор, источник питания, солнечная батарея и т. Д.
- устройство с сопротивлением ( R ), такое как свет, обогреватель, двигатель, телевизор и т. Д., Обозначенное общим названием резистор .
- проводов с незначительным сопротивлением для передачи тока ( I ) по замкнутому контуру от источника напряжения до резистора и обратно.

Сохранение заряда в контуре
- Ток, текущий в компонент, равен току, текущему на выходе.
Сохранение энергии в цепи
- Когда ток течет через источник напряжения, он испытывает повышение напряжения.
- Когда через резистор протекает ток, на нем падает напряжение.
- Когда ток течет по цепи, напряжение не изменяется.
Компоненты в последовательной цепи соединены по единому пути.
- В последовательной цепи ток везде одинаковый .
  I _с = I ₁ = I ₂ = I ₃ =… = I _i
- В последовательной цепи напряжение делится на , так что увеличение напряжения, подаваемое источником напряжения, равно сумме падений напряжения на резисторах.
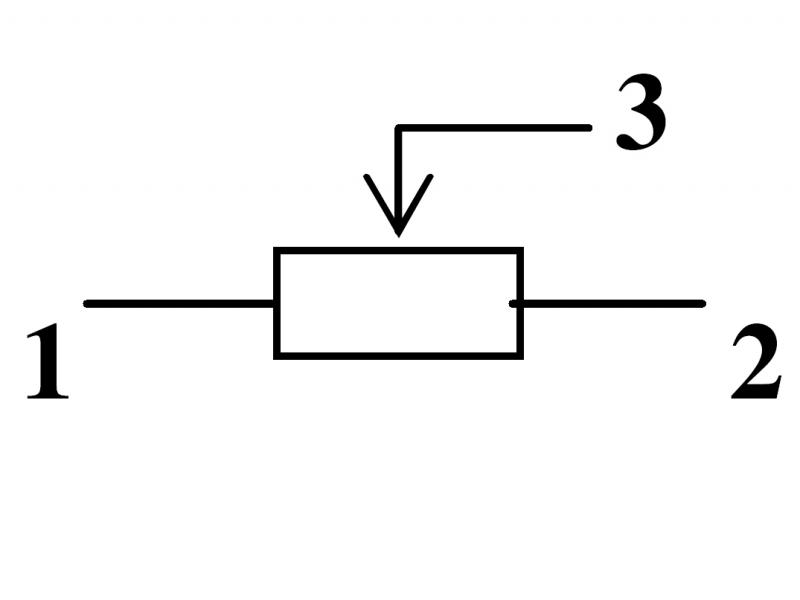
  В _с = В ₁ + В ₂ + В ₃ +… = ∑ В _i
- В последовательной цепи общее сопротивление равно сумме отдельных сопротивлений.
  R _с = R ₁ + R ₂ + R ₃ +… = ∑ R _i
  - Сопротивление увеличивается (и уменьшается ток), когда резисторы добавляются последовательно к источнику постоянного напряжения.
Компоненты в параллельной цепи лежат в независимых ветвях.
Метров в цепях
- Ток измеряется амперметром .
  - Амперметр подключается последовательно к элементу цепи или части исследуемой цепи.
  - Идеальный амперметр имеет нулевое сопротивление, поэтому он не увеличивает сопротивление и не снижает ток.
  - Обозначение амперметра – заглавная буква A⃝ в кружке.
- Напряжение измеряется вольтметром .
  - Вольтметр подключается параллельно элементу цепи или участку исследуемой цепи.
  - Идеальный вольтметр имеет бесконечное сопротивление, чтобы не уменьшать сопротивление и не увеличивать ток (чтобы не было короткого замыкания).
  - Обозначение вольтметра – заглавная буква V⃝ в кружке.
- Сопротивление измеряется омметром .
  - Омметр объединяет блок питания с амперметром и вольтметром.
  - Омметр «вычисляет» сопротивление по отношению напряжения к току.
  - Омметр представляет собой заглавную греческую букву Ω⃝ (омега) в круге.

Нет постоянных условий.

Механика
1. Кинематика
  1. Движение
  2. Расстояние и перемещение
  3. Скорость и скорость
  4. Разгон
  5. Уравнения движения
  6. Свободное падение
  7. Графики движения
  8. Кинематика и расчет
  9. Кинематика в двух измерениях
  10. Снаряды
  11. Параметрические уравнения
2. Динамика I: Сила
  1. Силы
  2. Сила и масса
  3. Действие-реакция
  4. Масса
  5. Динамика
  6. Статика
  7. Трение
  8. Силы в двух измерениях
  9. Центростремительная сила
  10. Кодовые рамки
3. Энергия
  1. Работа
  2. Энергия
  3. Кинетическая энергия
  4. Потенциальная энергия
  5. Сохранение энергии
  6. Мощность
  7. Машины простые
4. Dynamics II: Импульс
  1. Импульс и импульс
  2. Сохранение импульса
  3. Импульс и энергия
  4. Импульс в двух измерениях
5. Вращательное движение
  1. Кинематика вращения
  2. Инерция вращения
  3. Вращательная динамика
  4. Вращательная статика
  5. Угловой момент
  6. Энергия вращения
  7. Прокат
  8. Вращение в двух измерениях
  9. Сила Кориолиса
6. Планетарное движение
  1. Геоцентризм
  2. Гелиоцентризм
  3. Вселенская гравитация
  4. Орбитальная механика I
  5. Гравитационная потенциальная энергия
  6. Орбитальная механика II
  7. Плотность вытянутых тел
7. Периодическое движение
  1. Пружины
  2. Генератор простых гармоник
  3. Маятники
  4. Резонанс
  5. Эластичность
8. Жидкости
  1. Плотность
  2. Давление
  3. Плавучесть
  4. Расход жидкости
  5. Вязкость
  6. Аэродинамическое сопротивление
  7. Режимы потока
Теплофизика
1. Тепло и температура
  1. Температура
  2. Тепловое расширение
  3. Атомная природа вещества
  4. Закон о газе
  5. Кинетико-молекулярная теория
  6. Фазы
2. Калориметрия
  1. Явное тепло
  2. Скрытое тепло
  3. Химическая потенциальная энергия
3. Теплопередача
  1. Проводимость
  2. Конвекция
  3. Радиация
4. Термодинамика
  1. Тепло и работа
  2. Диаграммы давление-объем
  3. Двигатели
  4. Холодильники
  5. Энергия и энтропия
  6. Абсолютный ноль
Волны и оптика
1. Волновые явления
  1. Природа волн
  2. Периодические волны
  3. Интерференция и суперпозиция
  4. Интерфейсы и барьеры
2. Звук
  1. Природа звука
  2. Интенсивность
  3. Эффект Доплера (звук)
  4. Ударные волны
  5. Дифракция и интерференция (звук)
  6. Стоячие волны
  7. ударов
  8. Музыка и шум
3. Физическая оптика
  1. Природа света
  2. Поляризация
  3. Эффект Доплера (светлый)
  4. Черенковское излучение
  5. Дифракция и интерференция (свет)
  6. Тонкопленочная интерференция
  7. Цвет
4. Геометрическая оптика
  1. Отражение
  2. Преломление
  3. Зеркала сферические
  4. Сферические линзы
  5. Аберрация
Электричество и магнетизм
1. Электростатика
  1. Электрический заряд
  2. Закон Кулона
  3. Электрическое поле
  4. Электрический потенциал
  5. закон Гаусса
  6. Проводников
2. Электростатические приложения
  1. Конденсаторы
  2. Диэлектрики
  3. Батареи
3. Электрический ток
  1. Электрический ток
  2. Электрическое сопротивление
  3. Электроэнергия
4. цепей постоянного тока
  1. Резисторы в цепях
  2. Батареи в цепях
  3. Конденсаторы в цепях
  4. Правила Кирхгофа
5. Магнитостатика
  1. Магнетизм
  2. Электромагнетизм
  3. Закон Ампера
  4. Электромагнитная сила
6. Магнитодинамика
  1. Электромагнитная индукция
  2. Закон Фарадея
  3. Закон Ленца
  4. Индуктивность
7. цепей переменного тока
  1. Переменный ток
  2. RC цепи
  3. Цепи РЛ
  4. Цепи LC
8. Электромагнитные волны
  1. Уравнения Максвелла
  2. Электромагнитные волны
  3. Электромагнитный спектр
Современная физика
1. Теория относительности
  1. Пространство-время
  2. Масса-энергия
  3. Общая теория относительности
2. Quanta
  1. Излучение черного тела
  2. Фотоэффект
  3. Рентгеновские снимки
  4. Антиматерия
3. Волновая механика
  1. Волны материи
  2. Атомарные модели
  3. Полупроводники
  4. Конденсированные вещества
4. Ядерная физика
  1. Изотопы
  2. Радиоактивный распад
  3. Период полураспада
  4. Энергия связи
  5. Деление
  6. Fusion
  7. Нуклеосинтез
  8. Ядерное оружие
  9. Радиобиология
5. Физика элементарных частиц
  1. Квантовая электродинамика
  2. Квантовая хромодинамика
  3. Квантовая динамика вкусов
  4. Стандартная модель
  5. Помимо стандартной модели
Фонды
1. шт.
  1. Международная система единиц
  2. Гауссова система единиц
  3. Британо-американская система единиц
  4. Разные единицы
  5. Время
  6. Преобразование единиц
2. Измерение
  1. Значащие цифры
  2. По порядку величины
3. Графики
  1. Графическое представление данных
  2. Линейная регрессия
  3. Подгонка кривой
  4. Исчисление
4. Векторы
  1. Тригонометрия
  2. Сложение и вычитание векторов
  3. Векторное разрешение и компоненты
  4. Умножение векторов
5. ссылку
  1. Специальные символы
  2. Часто используемые уравнения
  3. Физические константы
  4. Астрономические данные
  5. Периодическая таблица элементов
  6. Люди в физике
Назад дело
1. Предисловие
  1. Об этой книге
2. Связаться с автором
  1. гленнелерт.сша
  2. Behance
  3. Instagram
  4. Твиттер
  5. YouTube
3. Аффилированные сайты
  1. hypertextbook.com
  2. midwoodscience.org

Роль резисторов в электрических цепях

Роль резисторов в электрической цепи: ПРИМЕЧАНИЕ: диаграммы, ссылки и практические вопросы в этот документ еще не добавлены: В электрических цепях постоянного (DC) или переменного (AC) тока, у которых есть резистор, как следует из его названия, сопротивляется потоку электронов.Это один из самых основных электрических компонентов. Его можно использовать для уменьшения доступного напряжения или тока в цепи. Хотя существуют различия в том, как резистор влияет на два разных типа источников тока (постоянного или переменного тока), в зависимости от конструкции резистора и задействованной частоты переменного тока, можно предположить, что нижеследующее в равной степени применимо к обоим. Для цепей переменного тока может потребоваться указать способ представления напряжения, среднее значение, пиковое значение или среднеквадратичное значение.Если не указывается тип напряжения переменного тока, обычно предполагается, что это значение (RMS).

Как обсуждалось в разделе Закона Ома, в электрической цепи напряжение (измеренное в вольтах и обозначенное буквой V) равно току (измеренному в амперах и обозначенному буквой I), умноженному на сопротивление (измеренное в Ом и обозначенное буквой I). буквой R) присутствует в цепи. Это представлено следующей формулой.

 V = IR или E = IR (закон Ома)

(Напряжение иногда обозначается буквой «E», что означает электродвижущую силу)

Электрическая цепь может включать в себя множество резисторов.То, как эти резисторы воздействуют на цепь, зависит от того, как они расположены в цепи. Резисторы могут быть расположены последовательно или параллельно источнику напряжения. См. Пример ниже.

На рисунке 1 представлена электрическая цепь с двумя последовательно включенными резисторами. Чтобы ток замкнул электрическую цепь, он должен течь от источника напряжения (B1) и проходить через резистор 1 (R1) и резистор 2 (R2), а затем обратно к B1.

Общее сопротивление в цепи представляет собой сумму двух номиналов резисторов (измеряется в омах, обозначается греческой буквой Ω).Следовательно, на рисунке 1 полное сопротивление цепи (RT) равно R1 + R2, что равно 100 Ом.

На рис. 2 представлена электрическая цепь с двумя параллельными резисторами. Чтобы ток замкнул электрическую цепь, он должен течь от источника напряжения (B1), а затем у тока есть два доступных пути, чтобы вернуться к B1. Часть тока пройдет через резистор 1 (R1) обратно в B1, а часть пройдет через резистор 2 (R2), а затем обратно в B1.

Общее сопротивление в параллельной цепи не так просто, как в последовательной цепи.Общее сопротивление в цепи на рисунке 2 является обратной величиной суммы обратной суммы двух номиналов резисторов (измеряется в омах, обозначается греческой буквой Ω). Следовательно, на рисунке 2 полное сопротивление цепи (RT) равно 1 / (1 / R1 + 1 / R2), что равно 25 Ом.

Важно отметить влияние на схему расположения резисторов. Используя закон Ома, мы можем определить, что полный ток, протекающий в каждой из двух цепей, значительно отличается, даже если для обеих использовались одни и те же компоненты.

Применяя небольшую алгебру к уравнению закона Ома, мы можем определить полный ток для каждой цепи.

Для схемы на рисунке 1 полный ток в цепи выражается уравнением: I = V / R. Подставляя известные нам числа, где V = 10 вольт и R = 100 Ом, мы получаем общий ток, протекающий в цепи, равный 10/100, что равняется 0,1 ампера.

Для схемы на рисунке 2 полный ток в цепи снова выражается уравнением: I = V / R.Подставляя известные нам числа, где V = 10 вольт и R = 25 Ом, мы получаем общий ток, протекающий в цепи, равный 10/25, что равняется 0,4 ампера.

Последовательные резисторы:

При последовательном использовании резисторы можно назвать «сетью деления напряжения». Это связано с тем, что в последовательной цепи ток, протекающий через каждый резистор, имеет одинаковое значение, но напряжение, присутствующее на каждом резисторе, составляет только часть общего значения напряжения цепи. Снова посмотрев на схему с рисунка 1, мы можем определить напряжение на каждом резисторе.

<Схема>

Основываясь на том факте, что в последовательной цепи ток, протекающий через каждый резистор, одинаков, мы снова можем использовать закон Ома, чтобы предсказать, какое напряжение будет присутствовать на каждом резисторе. Поскольку мы уже знаем, что общий ток цепи равен 0,1 А, а R1 равен 50 Ом, общее напряжение на R1 равно 0,1 А X 50 Ом = 5 вольт. Поскольку R2 имеет то же значение, что и R1, на R2 также будет подаваться 5 вольт.

Мы можем дважды проверить нашу математику, сложив вместе все напряжения, присутствующие на всех резисторах.В этом случае 5 В + 5 В = 10 В, что соответствует общему присутствующему напряжению.

Сопротивления параллельно:

При параллельном использовании резисторы можно назвать «токораспределительной сетью». Это связано с тем, что в параллельной цепи напряжение на каждом резисторе имеет одинаковое значение, но ток, протекающий через каждый резистор, составляет лишь часть общего значения тока цепи. Снова посмотрев на схему на рисунке 2, мы можем определить ток, протекающий через каждый резистор.

Основываясь на том факте, что в параллельной цепи напряжение на каждом резисторе одинаково, мы снова можем использовать закон Ома, чтобы предсказать, сколько тока будет протекать через каждый резистор. Поскольку мы уже знаем, что полное напряжение цепи равно 10 вольт, а R1 равно 50 Ом, общий ток, протекающий через R1, равен 10 В / 50 Ом = 0,2 ампера. Поскольку R2 имеет то же значение, что и R1, на R2 также будет подаваться 0,2 ампер.

Мы можем дважды проверить нашу математику, сложив вместе весь ток, протекающий через все резисторы.В этом случае 0,2 А + 0,2 А = 0,4 А, что согласуется с общим током, который мы ранее определили для рисунка 2.

Сопротивление сложной цепи:

В некоторых схемах вы найдете как последовательные, так и параллельные резисторы. Те же правила применяются в этих более сложных схемах, где присутствуют оба типа схем, как и в более простых схемах, где присутствует только одна. В случае сложных последовательных / параллельных резистивных цепей лучше всего переопределить параллельные части цепи в последовательную эквивалентную цепь, а затем использовать закон Ома для определения общего тока и присутствующего сопротивления.Затем вы можете использовать значения общего тока и напряжения для определения напряжений и токов, присутствующих на каждом из резисторов в цепи.

<ДИАГРАММА>

Начните с определения общего сопротивления параллельной комбинации R2 и R3, которое равно:

 [R2 & 3 = 1 / (1 / R2 + 1 / R3)] → [R2 & 3 = 1 / (1/100 + 1/400)] → [R2 & 3 = 1 / (0,01 + 0,0025)] → [R2 & 3 = 1 / (0,0125)] → R2 и 3 = 80 Ом

Затем вы можете перерисовать схему, показанную на рисунке 3, в последовательную эквивалентную схему, которая выглядит как рисунок 4.

<ДИАГРАММА>

Теперь мы можем определить полное сопротивление цепи, просто сложив все резисторы в последовательной эквивалентной схеме:

 [RT = R1 + R2 & 3 + R4 + R5] → [RT = 50 + 80 + 100 + 20] → RT = 250 Ом

Вооружившись общим сопротивлением цепи и полным напряжением цепи, теперь мы можем вычислить полный ток цепи, используя закон Ома:

 [VT = ITRT] → [IT = VT / RT] → [IT = 10 В / 250 Ом] → IT = 0,04 A

Теперь мы можем вычислить напряжение и ток, присутствующие на каждом из резисторов, используя закон Ома и два правила для цепей сопротивления:

1) В последовательной цепи ток одинаковый через все резисторы – цепь делителя напряжения.2) В параллельной цепи присутствующее напряжение одинаково для всех резисторов – цепи делителя тока.

Для R1:

 [VR1 = IT X R1] → [VR1 = 0,04 A X 50 Ом] → VR1 = 2 В

Для R2 и 3:

 [VR2 & 3 = IT X R2 & 3] → [VR2 & 3 = 0,04 A X 80 Ом] → VR2 и 3 = 3,2 В

Для R2:

 [IR2 = VR2 и 3 / R2] → [IR2 = 3,2 В / 100] → I R2 = 0,032 A

Для R3:

 [IR3 = VR2 & 3 / R3] → [IR2 = 3.2V / 400] → I R2 =.008A

Для R4:

 [VR4 = IT X R4] → [VR4 = 0,04 A X 100 Ом] → VR4 = 4 В

Для R5:

 [VR5 = IT X R5] → [VR5 = 0,04 A X 20 Ом] → VR5 = 0,8 В

Двойная проверка для проверки точности нашего анализа схемы подтверждает, что все отдельные напряжения, присутствующие на каждом резисторе в последовательной эквивалентной схеме, составляют в сумме 10 вольт, доступных от источника, а все токи в параллельной части схемы составляют полный ток по цепи 0.04А.

Резисторы

: рабочие и как использовать в схемах

Резистор

– это самый простой компонент, с которого начинает начинать каждый энтузиаст электроники или инженер, вступая в мир электроники. Поэтому, чтобы помочь новичкам, я собрал руководство, в котором я собираюсь объяснить работу резистора и ответить на эти три важных вопроса о резисторах.

Что такое резистор?
Как работает резистор?
Как использовать резистор в ваших схемах?

К концу этого руководства вы сможете объяснить, что такое резистор и как он работает, а также каковы наиболее важные области применения резистора в электронной схеме.Это руководство будет очень длинным, поэтому я настоятельно рекомендую вам добавить эту страницу в закладки и прочитать ее с небольшими перерывами.

ЧТО ТАКОЕ РЕЗИСТОР:

Резистор

– это пассивный компонент, который используется почти во всех печатных платах в электронике. Назначение резистора – показать сопротивление протекающему через него току, благодаря чему он получил название резистор (вы, должно быть, уже догадались). Сопротивление протеканию тока, проявляемое резистором, называется сопротивлением, и каждое сопротивление характеризуется значением сопротивления в Ом.

СОСТАВ РЕЗИСТОРА:

Состав резистора

Чтобы понять резистор, рассмотрите его как простой провод, который вместо того, чтобы позволить свободному потоку электронов через него, резисторы предлагают сопротивление и пытаются замедлить поток электронов AKA current. Резисторы обычно изготавливаются из таких материалов, как углерод, металл или пленка оксида металла. Свойство сопротивления резистора зависит от типа и количества смеси или материала, из которого он состоит. На приведенной выше диаграмме вы можете видеть смесь углерода между двумя выводами резистора, которая показывает сопротивление току.Подробнее о составе резисторов.

VI ХАРАКТЕРИСТИКИ РЕЗИСТОРА:

Напряжение-ток Характеристики резистора

Чтобы понять работу резистора, на мгновение понаблюдайте за приведенными выше характеристиками VI. VI – График вольт-амперных характеристик обычно показывает соотношение между напряжением и током для конкретного компонента. Характеристики VI для резистора довольно линейны. Как вы можете заметить, когда ток, протекающий через резистор, увеличивается, это приводит к увеличению напряжения, развиваемого на резисторе.Хотя разные резисторы с разным сопротивлением дают разные напряжения, когда через них протекает одинаковый ампер тока. Проще говоря, мы можем сказать, что напряжение на резисторе пропорционально току, протекающему через него. Да, резистор подчиняется закону Ома, поскольку их соотношение между током и напряжением является линейным по своей природе. Помните, что закон Ома гласит: «Ток, проходящий через проводник, прямо пропорционален напряжению, развиваемому на нем. Это дает начало популярной формуле V = IR

РЕЗИСТОРЫ ПОСЛЕДОВАТЕЛЬНО И ПАРАЛЛЕЛЬНО:

Использование более одного резистора может быть двух видов: последовательное и параллельное.На схеме выше показано подключение резисторов последовательно и параллельно. Важно помнить, что когда резисторы включены последовательно, сопротивление складывается. Между тем, когда резисторы включены параллельно, общее эквивалентное сопротивление уменьшается.

Эквивалентное сопротивление последовательных резисторов R1 и R2 будет Req = 10k + 10k = 20k

Эквивалентное сопротивление параллельных резисторов R1 и R2 будет 1 / Req = (1 / 10k + 1 / 10k) = 5K

Совет для быстрого решения проблемы параллельного сопротивления: если в цепи используются параллельные резисторы одинакового номинала, разделите значение резистора на количество резисторов, подключенных параллельно.Например, если 3 резистора по 10 кОм подключены параллельно, 10 кОм / 3 даст 3,33 кОм, что является эквивалентным сопротивлением.

ПРИМЕНЕНИЕ РЕЗИСТОРА:

Теперь мы подошли к самой интересной части этого урока. К настоящему времени вы должны иметь четкое представление о том, что такое резистор и как он работает. Давайте посмотрим на его приложения и на то, как он используется в схемах. Используется резистор

Как делитель напряжения для подачи опорного напряжения
Ограничители тока для предотвращения повреждения компонентов
Оставить отзыв
Как фильтры для входных сигналов
Цепи синхронизации для создания временной задержки
Подтягивающие и понижающие резисторы для фиксации логических уровней в цифровых схемах.
Нагрузочные резисторы

РАЗДЕЛИТЕЛЬ НАПРЯЖЕНИЯ:

Делитель напряжения

– довольно известная установка, использующая резисторы и широко используемая в схемах. Основная задача делителя напряжения – разделить входное напряжение на выходные. Это особенно полезно для создания опорного напряжения в наших схемах. Эталонные напряжения часто используются в компараторах, цепях датчиков, цепях запуска и т. Д. Давайте посмотрим на пример схемы, в которой делитель напряжения используется для создания опорного напряжения.

Резисторы в делителе напряжения

Как вы можете видеть на приведенной выше принципиальной схеме. Входное напряжение от Vcc составляет около +9 В на делитель напряжения, а выходное напряжение составляет 3 В. Здесь происходит то, что на резисторе R1 падает 6 В, а на R2 падает 3 В, всего 9 В. Выходное напряжение делителя напряжения определяется уравнением

Vout = Vin x R2 / (R1 + R2).

Vout = 9 В x 5 кОм / (10 кОм + 5 кОм)

= 3 В

Как уже говорилось, делитель напряжения широко используется в электронных схемах для создания опорного напряжения, смещения уровней сигналов и так далее.Но всегда помните, что делители напряжения не должны использоваться в качестве источника напряжения для силовых цепей. Если вы попытаетесь это сделать, напряжение на делителе значительно упадет. Это происходит из-за того, что делитель напряжения не может подавать ток для нужд цепей, поэтому он понижает напряжение, когда от него потребляется больше тока.

Еще несколько вещей, которые следует помнить о делителях напряжения: когда R1 и R2 равны, выходное напряжение будет составлять половину входного напряжения. Если R1 намного больше, чем R2 (R1 >> R2), то выходное напряжение будет близко или почти равно нулю.Когда R1 намного меньше, чем R2 (R1 << R2), результирующее выходное напряжение будет близко или почти равно входному напряжению. Эти вещи сэкономят вам время при анализе схем.

ОГРАНИЧИТЕЛЬНЫЙ РЕЗИСТОР ТОКА:

Это еще одно важное применение резистора. Как следует из названия, он ограничивает ток через цепь. Причина, по которой мы это делаем, заключается в том, что есть несколько случаев, когда нам нужно пропускать только определенное количество тока, иначе цепь / компонент может быть поврежден.Токоограничивающие резисторы обычно используются для светодиодов, двигателей, зарядки аккумуляторов, реле и т. Д.

Резистор для ограничения тока

Здесь в приведенной выше схеме показан токоограничивающий резистор для светодиода. Перейдем к расчетной части описанного выше ограничивающего резистора. Схема питается от батареи 9 В, однако светодиод, который у нас здесь, имеет прямое напряжение 2,2 В и потребляет всего 20 мА для работы. Поэтому нам нужно ограничить ток от батареи 9 В до 20 мА с помощью резистора.

R = V – V _{светодиод} / I _{светодиод}

= 9 – 2.2/20 мА

6,8 / 20 мА

= 340 Ом

и в качестве R1 выбираем ближайшее значение 330 Ом. Этот резистор на 330 Ом ограничивает ток до 20 мА для светодиода и защищает его от повреждения током. Приведенная выше формула применима, когда вам нужно ограничить ток двигателя, реле, батарей и т. Д.

РЕЗИСТОР КАК ЭЛЕМЕНТЫ ОБРАТНОЙ СВЯЗИ:

Обратная связь

– это концепция, используемая в операционных усилителях, широко известных как операционные усилители.Чтобы понять необходимость резистора в качестве элемента обратной связи, нам необходимо понять работу Opamp. Я не собираюсь вдаваться в подробности об операционных усилителях, но собираюсь немного поцарапать поверхность. Проще говоря, Opamp – это усилительное устройство, которое усиливает разницу между двумя входными клеммами (неинвертирующим и инвертирующим). Этот операционный усилитель имеет бесконечное усиление, что означает, что он способен бесконечно усиливать входной сигнал. Хотя это практически невозможно, но коэффициент усиления операционного усилителя настолько велик, что при подаче входного сигнала выходной сигнал достигает своего пикового напряжения насыщения.Мы не хотим этого в усилителе, потому что нам нужна усиленная копия нашего входного сигнала, и поэтому мы используем усилитель.

Отрицательная обратная связь

Если нам нужно получить усиленный сигнал от операционного усилителя, нам нужно контролировать его усиление. Для этой цели часть выходного сигнала возвращается на инвертирующий вход операционного усилителя, что делает его системой с отрицательной обратной связью. В приведенной выше схеме R1 – резистор обратной связи. Это подает часть выходного сигнала обратно на инвертирующий вход операционного усилителя. Отрицательная обратная связь влияет на усиление операционного усилителя и держит усиление под контролем.Таким образом, мы получим усиленный сигнал, который все еще можно использовать для наших целей. Итак, в двух словах, обратная связь – это корректирующий механизм в цепи, позволяющий цепи работать в стабильном и равновесном состоянии.

Для системы положительной обратной связи часть выходного сигнала возвращается на неинвертирующий вход операционного усилителя. Этот тип обратной связи используется для увеличения усиления. Положительная обратная связь не так широко используется, как конфигурация отрицательной обратной связи.

ФИЛЬТРЫ:

Резисторы

также используются для фильтрации входящих сигналов при использовании с конденсаторами.Фильтры широко используются во многих электронных схемах, где они пропускают сигнал определенной частоты и ослабляют нежелательные частоты. Есть две формы фильтров: пассивные и активные. Резистор является неотъемлемой частью пассивных фильтров наряду с конденсаторами и индукторами. Существует три важных типа фильтров, которые могут быть сконструированы с использованием пассивных компонентов, таких как резисторы, конденсаторы и индукторы. Фильтр низких частот, фильтр высоких частот и полосовой фильтр.

ФИЛЬТР НИЗКОГО ПРОХОДА:

Конструкция фильтра низких частот

Выше показан простой фильтр нижних частот, созданный с использованием резистора и конденсатора.Фильтр нижних частот пропускает только низкочастотные сигналы, то есть сигналы с частотой ниже частоты среза, и блокирует высокочастотные компоненты входящего сигнала. Здесь происходит то, что на низких частотах конденсатор демонстрирует высокое реактивное сопротивление по сравнению с резистором R. Напряжение на конденсаторе в этот момент очень высокое по сравнению с напряжением на резисторе. Поэтому он безопасно пропускает низкочастотные сигналы. На высоких частотах реактивное сопротивление конденсатора становится низким, и поэтому падение напряжения на резисторе становится большим, что ослабляет входящий сигнал.

ФИЛЬТР ВЫСОКОГО ПРОХОДА:

Конструкция фильтра высоких частот

Схема, показанная выше, представляет собой фильтр верхних частот, который ослабляет низкочастотный сигнал ниже точки отсечки и пропускает только высокочастотные сигналы. Здесь происходит то, что частота входящего сигнала очень низкая, конденсатор показывает высокое реактивное сопротивление, поэтому действует как разомкнутая цепь, приводящая к затуханию. Когда входная частота выше частоты среза, конденсатор демонстрирует низкое реактивное сопротивление, что позволяет сигналу проходить через него.

БАНДПАСНЫЙ ФИЛЬТР:

Конструкция полосового фильтра

Полосовой фильтр представляет собой комбинацию фильтров высоких и низких частот. В отличие от вышеупомянутых фильтров полосовые фильтры имеют две частоты среза. Следовательно, этот фильтр пропускает сигнал только в определенной полосе частот. Сигнал с частотой вне этого диапазона будет ослаблен.

Во всем вышесказанном очень важна частота среза, поскольку она определяет частоту, на которой сигнал будет проходить или ослабляться.Дизайн фильтра – довольно сложная концепция, которую нужно объяснить в этой статье, скоро для нее будет написано специальное руководство. В рамках данной статьи важно понимать роль резисторов в фильтрах.

ЦЕПИ ВРЕМЕНИ:

Использование резисторов в схемах синхронизации – довольно распространенное применение. Элементы синхронизации обычно известны как RC-цепи, в которых резистор и конденсатор работают вместе, чтобы генерировать определенную задержку времени на основе значений компонентов.

Схема синхронизации RC

Выше приведена RC-схема, в которой только резистор и конденсатор используются для создания требуемой задержки по времени.Это время регулируется формулой T = RC, где T называется постоянной времени. Таким образом, применение приведенных выше значений в данной формуле даст 1 секунду задержки с использованием этой схемы. Но это еще не все, что касается этой схемы, чтобы полностью понять RC-схему, вам необходимо понять работу конденсатора, особенно его кривую зарядки. Я не собираюсь подробно обсуждать работу конденсатора, но коснусь поверхности, чтобы лучше понять эту схему синхронизации и какова роль в ней резистора.

Когда напряжение, приложенное к конденсатору, течет через него, конденсатор постепенно начинает заряжаться. Это вызывает увеличение напряжения на его выводах. Напряжение на конденсаторе увеличивается постепенно, а не мгновенно, что приводит к временной задержке. Как только конденсатор достигает напряжения питания или Vcc, он прекращает зарядку и пропускает ток. В этом состоянии конденсатор считается полностью заряженным. Время, затрачиваемое от состояния нулевого заряда до состояния полного заряда, приводит к временной задержке, что показано кривой зарядки конденсатора, как показано на диаграмме ниже.

КРИВАЯ ЗАРЯДКИ:

Кривая заряда конденсатора

Если вы посмотрите на приведенную выше кривую зарядки, мы можем сделать вывод, что для достижения 100% заряда, что является подаваемым напряжением, требуется 5 Постоянная времени или 5 Тл. Как мы видели ранее, одна постоянная времени T = R x C, которая дает период времени только 63% от общего заряда конденсатора. Таким образом, для расчета времени, необходимого для полной зарядки конденсатора, используется формула T = 5 x R x C или 5T. Основная функция резистора в RC или синхронизирующей цепи – управлять потоком тока к конденсатору.Это повлияет на генерируемую задержку времени.

Итак, переходя к схеме выше, требуется 1 секунда или 1Тл, чтобы зарядить конденсатор до 63% от Vcc (9В). Конденсатору требуется 5 секунд или 5Т, чтобы достичь подаваемого напряжения 9 В. Таким образом, эта простая RC-схема способна генерировать временную задержку в 5 секунд. Этот RC-элемент используется вместе с другими цепями таким образом, что напряжение на конденсаторе контролируется как входное и достигается желаемая временная задержка.

РЕЗИСТОРЫ НА ВЫТЯЖЕНИИ И ВЫДВИЖЕНИИ:

Применение подтягивающих резисторов

Pull Up и Pull down резисторы – это то, что вы найдете в большинстве цифровых схем.Все мы знали, что цифровые схемы работают на логических уровнях. Давайте рассмотрим логику TTL, чтобы лучше это объяснить. В 5-вольтовых TTL-логических устройствах для достижения логического 0 входное напряжение должно быть в пределах от 0 до 0,8 В, тогда как для логической 1 входное напряжение должно быть в пределах от 2 до 5 В. Итак, что происходит, цифровые входные контакты очень чувствительны к электромагнитным помехам от внешнего окружения. Эти электромагнитные помехи индуцируют напряжение на этих входных контактах, что приводит к тому, что IC считывает неверный уровень напряжения.

Чтобы избежать этой вышеупомянутой ситуации, мы используем резисторы двумя способами: тянуть вверх и тянуть вниз.Подтягивающий резистор подтягивает уровень напряжения на входном выводе до уровня Vcc. Понижающий резистор понижает уровень напряжения на входных контактах до 0 В. Таким образом мы можем быть уверены, что наш цифровой входной контакт остается в предсказуемом состоянии.

Применение понижающих резисторов

Я написал подробное руководство по подтягивающим и понижающим резисторам и руководство по их использованию в схемах. Пожалуйста, прочтите это для получения дополнительной информации об этом.

НАГРУЗОЧНЫЙ РЕЗИСТОР:

В электронике Нагрузка относится к устройству или компоненту, который потребляет ток из цепи и подключен к ее выходу.Таким образом, нагрузочный резистор – это резистор, который подключается к выходному каскаду схемы для отвода тока из схемы. Термин «нагрузочный резистор» часто используется на практике при математическом моделировании схемы. Здесь любое устройство может использоваться со схемой для получения тока с ее выхода. В таких случаях резистор определенного номинала выбирается в качестве резистора нагрузки для имитации потребляемого тока, эквивалентного устройству, которое предназначено для использования на выходе. Проще говоря, резистор нагрузки используется для выполнения математических расчетов и анализа схемы на ее способность выдерживать ток, потребляемый под нагрузкой.

Использование резистора в качестве нагрузки

С учетом сказанного о нагрузочных резисторах есть случаи, когда нагрузочные резисторы будут частью практической схемы, а не использоваться только для математического моделирования. Есть регуляторы напряжения, где необходимо использовать нагрузочный резистор. В приведенной выше схеме резистор R1 используется в качестве резистора нагрузки. Это потребляет минимальный ток для поддержания стабильной работы регулятора. А в транзисторных усилителях обычно используется резистор нагрузки, чтобы предотвратить протекание избыточного тока между коллектором и эмиттером, что, в свою очередь, предотвращает повреждение транзистора.Таким образом, резисторы нагрузки используются для математического моделирования. Но есть случаи, когда он используется в практических схемах.

МОЩНОСТЬ РЕЗИСТОРА:

Это один из важных критериев резистора, о котором мы должны знать. Резисторы сопротивляются протеканию тока при заданном напряжении, когда это происходит, резистор нагревается из-за рассеиваемой мощности. Номинальная мощность – это не что иное, как количество мощности, которое резистор может безопасно рассеять. Когда рассеиваемая мощность превышает номинальную мощность резистора, он может быть разрушен или задымлен.У каждого резистора есть собственная номинальная мощность. Компоненты со сквозным отверстием обычно оцениваются как 0,25 Вт и имеют рейтинг выше этого.

Мощность, рассеиваемая на резисторе, может быть рассчитана по формулам P = I ² R или P = V ² / R. Предположим, вы последовательно подключаете светодиод 2,2 В, 12 В и резистор 330 Ом. В этом случае рассеиваемая мощность на резисторе составит

В _Разр. = 12 – 2,2 = 9,8 В

P = 9,8 ²/330 = 0.29 Вт

В этом случае вы должны использовать резистор 0,5 Вт для безопасной работы в цепи.

ЗАКЛЮЧИТЕЛЬНЫЕ СЛОВА:

Надеюсь, это руководство будет очень полезно для всех вас. Вышеупомянутые применения резисторов имеют большое значение и широко используются. Сделайте закладку на эту страницу и вернитесь позже. Если у вас есть какие-либо вопросы, связанные с этим руководством, пожалуйста, оставьте комментарий ниже. С радостью отвечу на них. Пожалуйста, поделитесь своими отзывами и мыслями об этом руководстве ниже.

Я работаю над учебниками по важным компонентам, используемым в электронике, и опубликую их в ближайшие дни. Подпишитесь на нашу еженедельную рассылку и следите за нами через каналы социальных сетей, чтобы получать обновления об этих уроках. Счастливого обучения 🙂

Связанное содержание

САМАЯ ПРОСТАЯ ЦЕПЬ:

ЗАКОН ОМА

САМАЯ ПРОСТАЯ ЦЕПЬ:

Мы можем заставить ток течь по кругу (цепи) соединяя клеммы аккумулятора вместе.Это растопит провод, разжигай искры и, возможно, разжигай огонь, так что не делай этого. Вместо этого подключите что-нибудь для управления током. Способность к управляющий ток называется сопротивлением, и все материалы имеют его в некоторой степени – на самом деле мы классифицируем материалы в соответствии с их сопротивление: с очень низким сопротивлением – проводники, с много сопротивления – изоляторы. Есть устройства, называемые резисторами которые используются в электронных гаджетах – у них есть сопротивление, которое что-то среднее между проводимостью и изоляцией и предсказуемо.Так вот безопасная цепь:

Батарея имеет определенное нажатие, называется электродвижущей силой или ЭДС. Это измеряется в единицах, называемых вольт . Обозначаем ЭДС (часто называемую напряжением) в формулах буквой E . Напряжение необходимо измерять между двумя точками цепи в таким же образом измеряется высота между двумя точками на сторона горы. Нет такого понятия, как «0 вольт», за исключением того, что напряжение между двумя точками равно 0, если они соединены вместе.

Резистор имеет определенную величину Сопротивление, измеренное в единицах, называется Ом . Мы указываем сопротивление в формулах с буквой R .

Когда ток течет, мы измеряем его в единицы называют ампер , и обозначают его буквой I .

Эти три связаны простой формулой называется законом Ома:

I = E / R

Также написано E = IR или R = E / I.

Это говорит нам ток, если мы знаем напряжение и сопротивление, или напряжение, если мы знаем ток и сопротивление, или сопротивление, если мы знаем ток и напряжение. Если вам это кажется немного замкнутым, вы правы. Мы можем измерить ток силой магнитного поля, которое он будет генерировать, но там не является критерием для измерения напряжения, кроме как увидеть, сколько тока течет через известное сопротивление. А как узнать сопротивление? Мы применяем известное напряжение и посмотрите, сколько тока течет.

Определение единиц также круглое: 1 ампер – это количество тока, протекающего через резистор сопротивлением 1 Ом. если приложено 1 вольт.

Два резистора последовательно:

Будет немного сложнее, если есть два резистора:

Какой бы ни был ток, он такой же в A, B и C. (Больше некуда течь ток).

Напряжение между A и C равно этому между A и B добавляется к тому, что между B и C.

E AC = E AB + E BC

Напряжения складываются, как и высота Дом – это сумма высот его этажей.

Напряжение на каждом резисторе равно пропорционально сопротивлению каждого резистора.

E AB / R 1 = E BC / рэнд 2

Видите ли, закон Ома верен для каждой части схема, а также схема в целом.Какой бы ток ни тек, на каждом резисторе оно одинаковое, поэтому напряжения будут регулироваться самих себя.

Суммарное сопротивление R 1 + р 2

Два параллельных резистора

Ток через А равен току через B плюс ток через C. Ток разделяется и идет вместе, как вода, текущая вокруг острова.

Напряжение на R 1 такое же, как на напряжение на R 2.

E AB = E AC, так I B R 1 = I C R 2 и I B / рэнд 2 = I C / R 1

Другими словами, ток через каждый резистор обратно пропорционален номиналам резисторов. Также важно помнить резистор высокого номинала проходит через небольшой Текущий.

Мы можем решить вышеуказанную проблему для полного тока ( I B + I C) и получите эквивалент сопротивление для двух резисторов:

В частном случае, когда резисторы То же, эквивалентное сопротивление составляет R 1 /2. Это появляется чаще, чем вы можно было ожидать.

В другом особом случае, когда R2 больше, чем 100-кратное значение R1, R2 составляет такую небольшую часть ток, который мы не удосужились включать в расчеты. Тогда мы говорим, что R2 не загружает схему.

Вот более сложный пример:

R1 – специальный тип резистора с регулируемым краном посередине.Это действительно заставляет R1 вести себя как два последовательно включенных резистора. Если мы скажем, что R2 в 100 раз больше R1, мы можем оставим это в расчетах и обнаружим, что напряжение E2 будет напрямую зависит от положения крана.

Если бы R2 было сопоставимо с R1 по стоимости, мы бы нужно вычислить, сначала решив R2 и нижнюю часть R1 как два резистора параллельно, и используя результат этого последовательно расчет, чтобы найти напряжение E2 и полный ток. В результирующая кривая напряжения (то, что вы получили бы, если бы построили E2 для различных положения крана) довольно беспорядочно, поэтому мы действительно предпочитаем R2, который не нагружает цепь.

Вернуться к темам Mu126

Резисторы

Что такое сопротивление?

Ограничение потока электронов или электрического ток до определенного уровня называется сопротивлением, а устройство или компонент, используемый для ограничения электрического тока, называется резистор.

Величина электрического тока, ограниченная резистор определяется с помощью уравнение закона.

Где R = сопротивление, V = напряжение, I = Электрический ток

Электрический ток, протекающий через резистор обратно пропорционален сопротивлению резистор и прямо пропорциональный напряжению приложенный к резистору.

В другими словами, количество электрического тока, протекающего через резистор уменьшается с увеличением сопротивления резистора (если напряжение, приложенное к резистору, остается постоянным) и увеличивается с увеличением напряжения, приложенного к резистор (если сопротивление резистора остается постоянным).

Что такое резистор?

Резисторы

– наиболее часто используемые электронные компоненты. в схемах. Резистор – это электронный компонент, который уменьшает или ограничивает поток электронов или электрического тока до определенного уровня.

Сколько электрического тока делает резистор блоков зависит от сопротивления резистора. Резисторы с большим сопротивлением блокирует большое количество электрического тока и пропускает очень небольшое количество электрического тока.Резисторы с меньшим сопротивлением блокирует очень небольшое количество электрического ток и допускает большое количество электрического тока. В электрический ток, блокируемый резистором, теряется в виде тепла.

Резисторы – это пассивные компоненты. Следовательно, они не могут контролировать поток электронов или электрический ток через них. Однако они могут ограничивать электрический ток до определенный уровень.

Резистор условное обозначение

Условное обозначение резистора показано на рисунок ниже. Резистор состоит из двух выводов. В клеммы резисторов используются для подключения к другим компоненты через электрический провод.

квартир резистора

Количество электрического тока, заблокированного резистор измеряется в омах и обозначается символом Ω.Ом – количество электрического тока, блокируемого резистором, и допустимый один ампер электрического тока при приложенном напряжении одного вольта остается постоянным.

Резистор относится к какая категория: изоляторы или проводники

Мы знаем, что материалы в основном засекречены на два типа: Изоляторы и проводники

Изоляторы блокируют большое количество электрических ток и допускает очень небольшое количество электрического тока, тогда как проводников позволяет электрический ток и блокирует очень небольшое количество электрический ток.

Резисторы с большим сопротивлением действуют как изоляторы, тогда как резисторы с меньшим сопротивлением действуют как проводники.

Сопротивление резистора в основном зависит от двух факторов: длины и площади поперечного сечения

Длина резистора

Сопротивление резистора напрямую пропорционально длине резистора.Длинная длина резисторы обладают высоким сопротивлением, потому что свободные электроны имеют путешествовать на большие расстояния. Следовательно, большое количество свободных электронов сталкиваются с атомами. Поэтому большое количество энергия или электрический ток будут потрачены впустую в виде нагревать.

Резисторы малой длины обеспечивают низкое сопротивление, потому что свободные электроны должны пройти только короткая дистанция.Следовательно, небольшое количество свободных электронов сталкивается атомы. Следовательно, только небольшое количество электрического тока впустую в виде тепла.

Площадь сечения резистора

Сопротивление резистора обратно пропорционально пропорционально площади поперечного сечения резистора. В резисторы с большой площадью поперечного сечения обеспечивают больше места для свободные электроны свободно перемещаются.Следовательно, столкновение свободных электронов с атомами меньше. Поэтому очень небольшое количество электрического тока тратится впустую.

Резисторы с малой площадью поперечного сечения обеспечивают очень маленькое пространство для свободных электронов. Следовательно столкновение свободных электронов с атомами больше. Следовательно, теряется большое количество электрического тока.

Преимущества и недостатки резисторов

Преимущества резисторов

Резисторы очень маленькие.Следовательно, это очень легко переносить их из одного места в другое.

Резисторы

очень дешевы. Следовательно, легко заменить их.

Резисторы не зависят от внешнего источник напряжения. Следовательно, внешнее напряжение или энергия не необходим для работы резисторов.

Недостатки резисторов

Резисторы с высоким сопротивлением будут противодействовать большое количество электрического тока.Следовательно, большое количество энергии тратится впустую в виде тепла.

Краткое руководство по электронике

УРОК 2 – РЕЗИСТОРЫ

При приложении напряжения электроны проходят через одни материалы легче, чем через другие.В металлах электроны удерживаются настолько свободно, что движутся почти беспрепятственно. Мы измеряем сопротивление электрическому току как сопротивление .

Резисторы

находятся где-то между проводниками, которые легко проводят, и изоляторами, которые вообще не проводят. Сопротивление измеряется в Ом после , открывшего закон, связывающий напряжение с током. Ом представлены греческой буквой омега.

Вернитесь к модели воды, текущей в трубе.Толщина трубы должна отражать сопротивление. Чем уже труба, тем труднее проходить воде и, следовательно, тем выше сопротивление. Для конкретного насоса время, необходимое для заполнения пруда, напрямую зависит от толщины трубы. Увеличьте трубу вдвое, и скорость потока увеличится вдвое, и пруд наполняется вдвое быстрее.

Резисторы, используемые в наборах MadLab, изготовлены из тонкой пленки углерода, нанесенной на керамический стержень. Чем меньше углерода, тем выше сопротивление.Затем на них наносят прочное внешнее покрытие и наносят цветные полосы.

Основная функция резисторов в цепи – контролировать прохождение тока к другим компонентам. Возьмем, к примеру, светодиод (свет). Если через светодиод проходит слишком большой ток, он разрушается. Таким образом, резистор используется для ограничения тока.

Когда через резистор протекает ток, энергия тратится и резистор нагревается. Чем больше сопротивление, тем горячее становится. Батарея должна выполнять работу, чтобы заставить электроны проходить через резистор, и эта работа превращается в тепловую энергию в резисторе.

Важное свойство резистора – это то, сколько тепловой энергии он может выдержать до того, как будет поврежден. Резисторы MadLab могут рассеивать около 1/4 Вт тепла (сравните это с бытовым чайником, который использует до 3000 Вт для кипячения воды).

Трудно сделать резистор на точное значение (да и в большинстве схем это все равно не критично). Сопротивления даны с определенной точностью или допуск . Это выражается как положительное или отрицательное значение процента.10% резистор с заявленным значением 100 Ом может иметь сопротивление в пределах от 90 до 110 Ом. Резисторы MadLab составляют 5% (это то, что означает золотая полоса), что более чем достаточно точности.

Реальные сопротивления варьируются в огромном диапазоне. В детекторе лжи есть резистор на 1 000 000 Ом рядом с резистором на 470 Ом. На принципиальных схемах вы часто видите букву «R» вместо омега для обозначения сопротивления. Это соглашение возникло еще до появления компьютеров и лазерных принтеров, когда греческие буквы редко можно было встретить на пишущих машинках.Буква «k» означает тысячу, а ее позиция показывает положение десятичной точки.

Вот несколько примеров:

     10R = 10 Ом
     10 кОм = 10 кОм = 10 000 Ом
     4k7 = 4,7 кОм = 4700 Ом

Закон Ома

Закон Ома на самом деле очень прост. Это говорит о том, что чем больше напряжения приложено к резистору, тем больше тока проходит через него. Если напряжение удваивается, то ток удваивается, если напряжение утроится, то увеличивается ток и т. Д.Для конкретного резистора всегда существует постоянное соотношение между напряжением и током. Это значение сопротивления, измеренное в Ом.

Чтобы определить сопротивление чего-либо, просто измерьте напряжение на нем и ток через него. Разделите первую цифру на вторую, и вы получите сопротивление.

Если вы знаете сопротивление и напряжение, вы можете рассчитать ток. Или, если вы знаете сопротивление и ток, вы можете рассчитать напряжение. Это делает закон Ома очень полезным.

Цветовой код резистора

Цветовой код резистора – это способ показать номинал резистора. Вместо обозначения сопротивления на его корпусе, которое часто было бы слишком мало для чтения, используется цветовой код. Десять разных цветов представляют числа от 0 до 9. Первые две цветные полосы на теле – это первые две цифры сопротивления, а третья полоса – «множитель». Множитель просто означает количество нулей, добавляемых после первых двух цифр. Красный представляет собой цифру 2, поэтому резистор с красными, красными и красными полосами имеет сопротивление 2, за которым следуют 2, за которыми следуют 2 нуля, что составляет 2 200 Ом или 2.2 кОм.

Последняя полоса – это допуск (точность). Все резисторы MadLab составляют 5%, что показано золотой полосой.

Вот полный список цветов:

  1-я полоса 2-я полоса 3-я полоса 
     Черный 0 0 x 1
     Коричневый 1 1 x 10
     Красный 2 2 x 100
     Апельсин 3 3 x 1000
     Желтый 4 4 x 10000
     Зеленый 5 5 x 100000
     Синий 6 6 x 1000000
     Фиолетовый 7 7
     Серый 8 8
     Белый 9 9

Вот несколько примеров:

     Желтый, фиолетовый, красный, золотой = 47 x 100 = 4700 Ом = 4.7 кОм
     Коричневый, черный, желтый, золотой = 10 х 10 000 = 100 кОм
     Желтый, фиолетовый, черный, золотой = 47 x 1 = 47 Ом
     Коричневый, черный, красный, золотой = 10 x 100 = 1000 Ом = 1 кОм
     Коричневый, черный, зеленый, золотой = 10 x 100 000 = 1 000 кОм = 1 МОм
     Все +/- 5%

Переменные резисторы

Неудивительно, что переменные резисторы – это резисторы, сопротивление которых можно изменять. Переменные резисторы MadLab (называемые пресетами ) имеют металлический стеклоочиститель, покоящийся на круговой дорожке из углерода.Стеклоочиститель движется по дорожке при повороте предустановки. Ток проходит через стеклоочиститель, а затем через часть углеродистой дорожки. Чем больше трасса должна пройти, тем больше сопротивление.

Пресеты

MadLab имеют три ножки. Верхняя опора соединяется со стеклоочистителем, а две другие опоры – с двумя концами гусеницы. Обычно фактически используется только одна из опор гусеницы.

Переменные резисторы используются в схемах для изменения вещей, которые нужно изменить, например, громкости и т. Д.

СЛЕДУЮЩИЙ УРОК | СОДЕРЖАНИЕ Цепи серии

Представьте себе электрический ток, выходящий из батареи. Если резисторы подключены в такой способ, которым часть тока может проходить через один резистор, а остальная часть ток может проходить через другой резистор, тогда цепь параллельна Схема .

I _T – полный ток параллельной цепи.Вы бы измерили этот ток в любом месте до или после трехканального разветвителя, ведущего к трем резисторам. В между перекрестком и R ₁, вы бы измерили I ₁. Между перекрестком и R ₂, вы бы измерили I ₂ и т. д.

Поскольку общий ток I _T делится на три разные группы электронов, путешествующих каждый своим путем,

I _T = I ₁ + I ₂ + I ₃ +.

В параллельных цепях все резисторы, независимо от их сопротивления, испытывают одинаковое падение напряжения или разность потенциалов, потому что все они имеют одинаковые точки входа и выхода (переходы).

V _T = V ₁ = V ₂ = V ₃ = V _n

Если разделить формулу тока по соотношению напряжений получаем:

или _{рэнд T} = [₁ ^-1 + ₂ ^-1 + ₃ ^-1 +] ^-1

Пример 1

а. Какое полное сопротивление цепи?

R _T = [₁ ^-1 + R ₂ ^-1 + R ₃ ^-1] ^-1

R _T = [12 ^–1 + 12 ^–1 +12 ^–1] ^–1 = 4 Вт

г. Какой общий ток?

I _T = V / R _T = 12/4 = 3 A

г.Какое напряжение (_{В 1}) будет измеряется на каждом отдельном резисторе?

12 В (напряжение постоянно параллельно.)

г. Какой ток отводится каждый резистор?

I ₁ = V / R ₁ = 12/12 = 1A. Остальные тоже нарисуйте по 1 А, всего 3 А.

Пример 2

рисунок кажется запутанным, но обратите внимание, что это параллельная схема, потому что у электронов есть выбор.На стыке (показано красной точкой) электроны следуйте либо зеленому маршруту, либо оранжевому маршруту.

Используйте I

₁ = 1A; I ₂ = 0,5 А; _{рэнд 1} = 10Вт.

Найдите V ₂.

Помните, что параллельное напряжение постоянно. Итак, если мы найдем V ₁, мы будем знать V ₂.

В ₁ = I ₁ R ₁ = 1 (10) = 10 В.

В ₂ = В ₁ = 10 В.

Найдите R ₂.

R ₂ = V / I ₂ = 10 / 0,5 = 20 Вт.

Используйте два метода, чтобы получить R _T.

(1) R _T = [R ₁ ^-1 + R ₂ ^–1] ^–1 = [20 ^–1 + 10 ^–1] ^-1 = 6.7 Вт.

(2) я _т = I ₃ = I ₁ + I ₂ = 1 + 0,5 = 1,5 А.

R _T = V / I _T = 10 / 1,5 = 6,7 W.

Пример 3

В параллельной цепи какой эффект дает добавление еще резисторов иметь по общему току?

Ток увеличивается !

В цепи серии добавление резисторов увеличивает общее сопротивление и, таким образом, снижает ток.Но в случае с параллельная схема, потому что добавление дополнительных резисторов параллельно создает больше вариантов а снижает общее сопротивление . Если такая же батарея подключена к резисторы, ток увеличится. Не убежден? Попробуйте:

[10 ^-1 + 10 ^-1] ^-1 = 5 Вт, но добавьте подключите резистор параллельно, и вы получите [10 ^-1 + 10 ^-1 + 10 ^-1] ^-1 = всего 3,3 Вт. чем меньше сопротивление, тем выше общий ток.

Еще одна интересная особенность параллельных цепей заключается в том, что если один компонент отключен, другие пути все еще жизнеспособны, так что электроны могут продолжать течь по цепи.

Резистор схема: Резисторы: описание, подключение, схема, характеристики

Схемы соединения резисторов

Последовательное соединение резисторов

Параллельное соединение резисторов

Реостат

Гасящий резистор

Делитель напряжения

Потенциометр

Схемы защиты ТН от феррорезонанса

Переменный резистор | Электроника для всех

Переменный резистор с ДУ » S-Led.Ru

Переменные и подстроечные резисторы. Реостат.

Переменный резистор.

Подстроечный резистор.

Реостат.

Потенциометр.

Резисторы переменные, постоянные вся истина!

Что такое сопротивление?

Как выглядит резистор?

Постоянные резисторы.

Переменные резисторы

Формулы и свойства

Последовательное соединение резисторов

Параллельное соединение резисторов

Преобразование звезды в треугольник и обратно

Как выбрать подходящий резистор

Итак… что такое резистор?

Какие бывают резисторы?

Тип конструкции

Резистивный материал

Как используются резисторы?

Как измеряется номинал резистора?

Цветовая маркировка

Резисторы для поверхностного монтажа – SMD-резисторы

Как выбрать подходящий резистор

Шаг 1 – Расчет требуемого сопротивления

Шаг 3 – Выбор резистора

в схемах – Резюме – Гипертекст по физике

Сводка

Роль резисторов в электрических цепях

: рабочие и как использовать в схемах

ЧТО ТАКОЕ РЕЗИСТОР:

СОСТАВ РЕЗИСТОРА:

VI ХАРАКТЕРИСТИКИ РЕЗИСТОРА:

РЕЗИСТОРЫ ПОСЛЕДОВАТЕЛЬНО И ПАРАЛЛЕЛЬНО:

ПРИМЕНЕНИЕ РЕЗИСТОРА:

РАЗДЕЛИТЕЛЬ НАПРЯЖЕНИЯ:

ОГРАНИЧИТЕЛЬНЫЙ РЕЗИСТОР ТОКА:

РЕЗИСТОР КАК ЭЛЕМЕНТЫ ОБРАТНОЙ СВЯЗИ:

ФИЛЬТРЫ:

ФИЛЬТР НИЗКОГО ПРОХОДА:

ФИЛЬТР ВЫСОКОГО ПРОХОДА:

БАНДПАСНЫЙ ФИЛЬТР:

ЦЕПИ ВРЕМЕНИ:

КРИВАЯ ЗАРЯДКИ:

РЕЗИСТОРЫ НА ВЫТЯЖЕНИИ И ВЫДВИЖЕНИИ:

НАГРУЗОЧНЫЙ РЕЗИСТОР:

МОЩНОСТЬ РЕЗИСТОРА:

ЗАКЛЮЧИТЕЛЬНЫЕ СЛОВА:

Связанное содержание

САМАЯ ПРОСТАЯ ЦЕПЬ:

Резисторы

Что такое сопротивление?

Что такое резистор?

Резистор условное обозначение

квартир резистора

Резистор относится к какая категория: изоляторы или проводники

Сопротивление резистора в основном зависит от двух факторов: длины и площади поперечного сечения

Длина резистора

Площадь сечения резистора

Преимущества и недостатки резисторов

Преимущества резисторов

Недостатки резисторов

Краткое руководство по электронике

Пример 1

Пример 2

Используйте I

Пример 3

Больше новостей

Добавить комментарий Отменить ответ