Схема ампервольтметра: Tool Electric: Схема ампервольтметра YB27VA

Содержание

Схема и конструкция авометра

Авометр, схема которого приведена на рис. 1, позволяет измерять:

постоянные и переменные напряжения на шкалах:0,15; 0,5; 1,5; 5; 15; 50; 150; 500 в;
постоянный и переменный ток на шкалах 50; 150; 500 мка, 1,5, 5; 15; 50; 150; 500 и 1500 ма;
сопротивления до 2 Мом на пяти шкалах (середины шкал соответствуют 10, 100, ‘1000 ом, 10 и 100 ком).

Входное сопротивление прибора при измерении постоянного и переменного напряжения равно 20 ком/в. Падение напряжения на внутреннем сопротивлении прибора при измерении тока не превышает 100 мв.

Габариты прибора 125X73X45 мм, вес в латунном футляре 400 г. Основные узлы прибора — гальванометр с чувствительностью 50 мка, усилитель мощности на транзисторе Т1, детектор и система коммутации.

Принципиальная схема

При измерении напряжения, постоянного тока и сопротивлений переключатель рода измерения В2 устанавливают в положение « = ». При этом батарея питання Б2 от усилителя отключается, а гальванометр цА через контакты переключателя ВЗ или резистор R29 подключается к ползунку переключателя рода и пределов измерений В1. Одновременно переключатель В2а отключает вход усилителя.

Рис. 1. Схема и конструкция авометра.

Измеряемое постоянное напряжение подводится к гнездам 1— 2. Пределы измерения устанавливаются переключателем В1, который включает последовательно с измеряемым напряжением и гальванометром один из резисторов R1— R8.

При измерениях постоянных напряжений образуется цепь: гнездо 1 (плюс), резистор R28, гальванометр цА .контакты 0 -1 переключателя В2в, контакты 0-1 переключателя В3, контакты 1—8 переключателя В1, одни из добавочных резисторов R1— R8, гнездо 2 (минус).

Для измерения постоянного тока используют гнезда 1 и 3. В этом случае образуется цепь: гнездо 1 (плюс), один из шунтов R9— R17, контакты 9— 17 переключателя В1, гнездо 3 (минус). Падение напряжения на одном из шунтов измеряется вольтметром, который образован гальванометром с учетом его внутреннего сопротивления и добавочным резистором R28.

Входное сопротивление вольтметра в этом случае составляет 2 ком, что соответствует шкале вольтметра 100 мв. 4». В этом случае последовательно с измерительным прибором включают батарею Б2 н эталонный резистор R21.

При измерении переменного напряжения и тока переключатель В2 устанавливают в положение При этом в схему будет включен усилитель переменного-тока, смонтированный по схеме с общим эмиттером на транзисторе Т1.

Секцией В2б переключателя В2 к усилителю подключается батарея Б2, а секцией В2в — гальванометр цА, который измеряет постоянную составляющую тока на выходе выпрямителя (диод Д1). Измеряемое напряжение подается на вход усилителя с зажимов 1— 2 через резисторы R1— R8 и конденсаторы C1, С2.

Для увеличения стабильности работы усилителя при изменении питающего напряжения на базу транзистора 77 через резистор R24 с коллектора подается напряжение отрицательной обратной связи. Этим же резистором подбирается режим работы транзистора.

Для того чтобы одни и те же добавочные резисторы в схеме вольтметра (R1— R8) использовать при измерении постоянного н переменного напряжения, необходимо, чтобы входное сопротивление усилителя было равно сопротивлению цепи измерительного прибора. В данном случае все сопротивления эталонных резисторов рассчитаны на входное сопротивление прибора 2 ком. Такое же входное сопротивление должно быть н у усилителя, на входе которого включен резистор R22, с помощью которого добиваются необходимой величины — 2 ком.

Чтобы исключить влияние постоянной составляющей на показания индикатора при подаче на вход вольтметра пульсирующего напряжения, последовательно с добавочными резисторами включены два конденсатора С1, С2 со встречной полярностью. Для повышения линейности шкалы вольтметра переменного тока и уменьшения чувствительности индикатора до нужной величины в детекторную цепь включен резистор R27.

Работа схемы авометра при измерении переменных напряжений и токов отличается от работы прибора на постоянном токе только тем, что индикаторная часть прибора заменяется усилителем переменного тока, на выходе которого имеется детекторная цепь, нагруженная на микроамперметр цА.

Детали и конструкция

Общий вид прибора приведен на рис. 2. Передняя панель изготовлена из гетинакса толщиной 4 мм. На ее лицевой панели расположены: гальванометр цА, ручки управления переключателями В1, В2, н резистором R30, гнезда 1— 6. Все остальные детали авометра крепят на задней монтажной панели, которая также изготовлена нз гетинакса толщиной 2 мм. Футляр сделан из латуни толщиной 1 мм.

В приборе применены резисторы типа УЛМ и МЛТ, конденсаторы типа ЭТО. Резисторы R9—R16, R18 — проволочные. Гальванометр типа М-592 с сопротивлением около 1900 ом. Переключатель В1 применен от телефонной аппаратуры. Переключатели В2 и В3 изготовлены на базе контактных групп от типовых телефонных реле. Конструкция их может быть самой разнообразной.

Налаживание авометра производят в следующей последовательности: проверив монтаж, добиваются, чтобы авометр исправно работал при измерении постоянных напряжений, токов н сопротивлений. Затем переходят к регулировке усилителя, которая сводится к подбору сопротивлений резисторов R24, R23 и R22.

Для этого, установив переключатель В2 в положение «~», подбором сопротивления резистора R24 добиваются нужного напряжения на коллекторе (3,5 в). Подгонка чувствительности усилителя по напряжению осуществляется резистором R23.

Подключив к точкам Л и В низкоомный выход звукового генератора при наприжении 100 мв, изменением сопротивления резистора R23 добиваются, чтобы стрелка гальванометра цА отклонилась на всю шкалу.

Закончив работу по установке чувствительности усилителя, переходят к калибровке его входного сопротивления. С этой целью, не изменяя .величины напряжения, подаваемого с выхода звукового генератора (100 мв), последовательно со звуковым генератором включают резистор с сопротивлением 2 ком, н входное напряжение от ЗГ устанавливают равным 200 мв, т. е. увеличивают его в 2 раза.

Подбором сопротивления резистора R22 добиваются, чтобы стрелка гальванометра снова отклонилась на всю шкалу. Очевидно, что в этом случае входное сопротивление усилителя переменного тока будет равно 2 ком.

Произведя вышеуказанные регулировки, отключают звуковой генератор и проверяют напряжение на коллекторе транзистора 77. Если оно изменилось более чем на 20%, надо заново подобрать сопротивления резисторов R24, R23, R22. Окончательную калибровку усиления производят подбором сопротивления резистора R27.

Налаживание производят на частоте 50 гц. Для переменного тока прибор имеет две шкалы (5 и 15 в), для постоянного — две и одну для сопротивлении.

В нерабочем положении переключатель В2 должен находиться в положении, соответствующем измерению постоянного тока, так как питание усилителя при этом отключается.

Схема авометра разработана радиолюбителем М. Балашовым.

Источник: С. Л. Матлин – Радиосхемы (пособие для радиокружков), 1974г.

Вольтамперметр 100 Вольт 10 А

Возникла идея обзавестись лабораторным блоком питания. Цены на готовые кусаются, а вот собрать самому вполне по силам. Для визуализации выходных параметров задуманного блока питания был преобретен китайский готовый ампервольтметр постоянного тока.

Основные характеристики устройства как нельзя лучше подходят для отображения выходного напряжения и тока потребления БП, а именно:
— диапазон измерения: 0-100 В 0-10A
— рабочий ток: ≤20mA
— точность измерения: 1%
— дисплей: 0. 28 ” (Два цвета красный (напряжение) и синий (сила тока)
— минимальный шаг измерения напряжения: 0.1 В
— минимальный шаг измерения силы тока: 0.01A
— рабочая температура: от-15 до 70 ° c
— размер: 47 × 28 × 16 мм
ПРИМЕЧАНИЕ: рабочее напряжение, необходимое для работы электроники ампервольтметра: 4,5 – 30 В

Приезжает посылка в антистатическом пакет

В комплект входит сам ампервольтметр и два шлейфа

На плате присутствуют легкие следы флюса, токоизмерительный шунт присутствует, хотя на фотографиях на странице продавца его нет.

Шунт впаян с наклоном к разъему, что пришлось исправить отгибанием шунта

При подключении и сравнении показаний с показаниями мультиметра, расхождения составили 0,2 Вольта. Производитель предусмотрел подстроечные сопротивления на плате для калибровки показаний напряжения и тока, что является большим плюсом.

На мой взгляд, корпус устройства немного маловат – светодиодные матрицы вплотную прилегают к внутренней стороне корпуса и при установке модуля в лицевую панель приборов фиксаторам не оставлено место для маневра.

Две светодиодных матрицы по высоте точно совпадают с высотой платы, видимо при установке модуля в лицевую панель фиксаторы придется «слегка обработать напильником»).

Сегменты светятся прилично ярко, цветовая гамма подобрана очень удачно. Не заметить их сигналов будет трудно, за что производителю большой плюс.

Отдельно хочу разъяснить способы подключения ампервольтметра. Поскольку на странице продавца нет данной информации, то пришлось покопаться в сети и набросать пару схем.
Поскольку электронная начинка ампервольтметра питается напряжением 4,5-30 вольт, то есть два способа подключения:
1.Если источник измеряего напряжения работает в диапазоне от 4,5 до 30 Вольт, то тогда схема подключения выглядит так:

2. Если источник измеряемого напряжения работает в диапазоне 0 -4,5 В или выше 30 Вольт, то до 4,5 Вольт ампервольтметр не запустится, а при напряжении более 30 Вольт он просто выйдет из строя, во избежание чего следует воспользоваться следующей схемой:

О проводах из комплекта:
— провода трехконтактного разъема тонкие и выполнены проводом 26AWG – толще тут и не нужно.

Цветная изоляция интуитивно понятна – красный это питание электроники модуля, черный это масса, желтый — измерительный провод;
— провода двухконтрактного разъема – это провода токоизмерительные и выполнены толстым проводом 18AWG. Для подключения нагрузки рекомендую использовать такой же.
В целом, при цене в 2,5 $, описанный ампервольтметр, закрыв глаза на остатки флюса и возможные трудности с установкой в толстостенную лицевую панель, считаю весьма удачным приобретением.
Дополнительная информация!
Как стало ясно из комментариев к обзору, в некоторых экземплярах наблюдается отличные от нуля показания амперметра без нагрузки.
Оказалось, что решить проблему можно сбросом показаний амперметра как показано ниже:

Картинку стянул с другого ресурса — прошу сильно не пинать.

Планирую купить +28 Добавить в избранное Обзор понравился

+20 +32
Схема амперметра и вольтметра
Вольтметры и амперметры используются для измерения напряжения и силы тока соответственно. Здесь мы обсудим схемы амперметра и вольтметра.
Амперметр
Вольтметр
Амперметр
Амперметр представляет собой гальванометр низкого сопротивления, используемый для измерения силы тока в электрической цепи.
Амперметр всегда подключают последовательно в цепи, потому что, когда амперметр подключен последовательно, он не изменяет заметно сопротивления цепи и, следовательно, основного тока, протекающего через цепь.
В идеальном случае амперметр имеет нулевое сопротивление.
Показания амперметра всегда меньше фактического тока в цепи, потому что все практические амперметры имеют низкое конечное сопротивление.
Чем меньше сопротивление амперметра, тем точнее будут его показания.
Гальванометр можно преобразовать в амперметр, подключив шунт низкого сопротивления параллельно катушке гальванометра. Схема амперметра: Здесь $\mathrm{I}_{9} \mathrm{G}=\left(\mathrm{I}-\mathrm{I}_{\mathrm{g}}\right) \mathrm{S}$ или $\quad S=\frac{I_{g}}{I-I_{g}} G$ Здесь G — сопротивление гальванометра, а $I_{g}$ — сила тока, необходимая для получения полного отклонения тока.

Шунт (S): Это низкоомное сопротивление, подключенное параллельно катушке гальванометра для преобразования его в амперметр. Он защищает гальванометр от сильных токов. Он также используется для изменения диапазона амперметра.
Сопротивление преобразованного амперметра $R_{A}=\frac{G S}{G+S}$
Диапазон амперметра увеличивается за счет уменьшения сопротивления шунта S. Если $\mathrm{I}=\mathrm{N} \mathrm{I}_{\mathrm{g}}$, то $S=\frac{I_{g}}{N I_{g}-I_{g} } G=\frac{G}{N-1}$ Диапазон амперметра можно увеличить в N раз, уменьшив шунт до S = G/N-1. 9{2} S / \rho$, где r – радиус шунтирующего провода, а  – удельное сопротивление материала шунтирующего провода.
Уменьшение сопротивления шунта может увеличить диапазон, но снижает чувствительность.

Вольтметр
Вольтметр представляет собой гальванометр высокого сопротивления, используемый для измерения разности потенциалов.
Вольтметр подключен параллельно элементу цепи, потому что при параллельном подключении он потребляет наименьший ток от основного тока. Таким образом, он измеряет почти точную разность потенциалов.
Идеальный вольтметр имеет бесконечное сопротивление.
Показания вольтметра всегда меньше фактического значения, потому что все практические вольтметры могут иметь большое, но конечное сопротивление.
Чем больше сопротивление вольтметра, тем точнее его показания.
Гальванометр преобразуется в вольтметр путем последовательного включения высокого сопротивления с катушкой гальванометра. $V=I_{g}(R+G) \quad$ или $\quad R=\frac{V}{I_{g}}-G$
Сопротивление преобразованного вольтметра $\mathrm{R}_{\mathrm{v}}=\mathrm{R}+\mathrm{G}$

Диапазон вольтметра увеличивается за счет увеличения последовательного сопротивления. Если $\quad \mathrm{V}=\mathrm{NV}_{9}=\mathrm{NI}_{9} \mathrm{G} \quad$, то $\quad R=\frac{N I_{9 } G-G}{I_{9}}=(N-1) G$ Значение сопротивления, необходимое для увеличения дальности в $N$ раз, равно $R=(N-1) G$
.
Пример. Какова величина шунта, пропускающего 10% основного тока через гальванометр $99\Омега ?$ Сол.
$S =\frac{I _{g} G }{I – I _{g}}$
, где $I_{9}=\frac{10}{100} I=0,1 I$
Итак, $S=\frac{0,1 I \times 99}{I(1-0,1)}=\frac{9,9 {0,9}=11 Омега$.
Читайте также:
Виды и действие электрического тока

Закон Ома и сопротивление
Комбинация сопротивлений
ЭДС и внутренние сопротивления ячейки
Элементы, соединенные последовательно, параллельно и смешанно
Круговой закон Кирхгофа
Электрические токи в проводниках
Мост Уитстона
Почтовый ящик
Мост Уитстона
Гальванометр с подвижной катушкой
Амперметр и вольтметр
Принцип работы потенциометра
Скачать приложение eSaral
Амперметр и вольтметр Схема амперметра и вольтметра Текущий класс электричества 12 Физика JEE
Весь учебный материал
Амперметр: определение, измерения и функции
Вы, вероятно, использовали амперметр в физической лаборатории для измерения силы тока в электрической цепи. Амперметры полезны не только для учебных целей и понимания потока электронов, но и являются жизненно важной частью многих электрических систем вокруг нас. После того, как схема, намного более сложная, чем построенная на уроке физики в старшей школе, построена, важно проверить ее функциональность. Некоторые примеры включают электричество в зданиях, двигатели в автомобилях и блок питания компьютера. Если ток, протекающий через определенную систему, превышает ее пределы, это может привести к неисправности и даже стать опасным. Вот где амперметр пригодится. В этой статье мы обсудим различные теоретические и практические аспекты амперметров!
Определение амперметра
Измерение электрического тока является важным аспектом оценки работы различных электронных и энергетических систем. Мы можем сделать это, используя амперметр , показанный на рисунке 1 ниже.
Рис. 1 – Типовой амперметр с двумя диапазонами измерений.
Амперметр — это инструмент, используемый для измерения силы тока в определенной точке цепи.
Легко запомнить, так как название напрямую связано с измерением силы тока – амперами. Он всегда должен быть подключен в серии с элементом, в котором измеряется ток, так как в этом случае ток остается постоянным.
Идеальный амперметр имеет нулевое сопротивление, то есть он не влияет на ток в элементе, с которым он соединен последовательно. В действительности это, очевидно, не так: все амперметры имеют хотя бы некоторое внутреннее сопротивление, но оно должно быть как можно меньше, так как любое присутствующее сопротивление изменит измерения тока. Пример проблемы сравнения двух случаев можно найти далее в этой статье.
Эквивалентным инструментом для измерения разности электрических потенциалов между двумя точками цепи является вольтметр . Подключив вольтметр до и после потребителя (например, резистора), мы можем измерить падение напряжения.
Символ амперметра
Как и любой другой компонент электрической цепи, амперметр имеет свой собственный символ.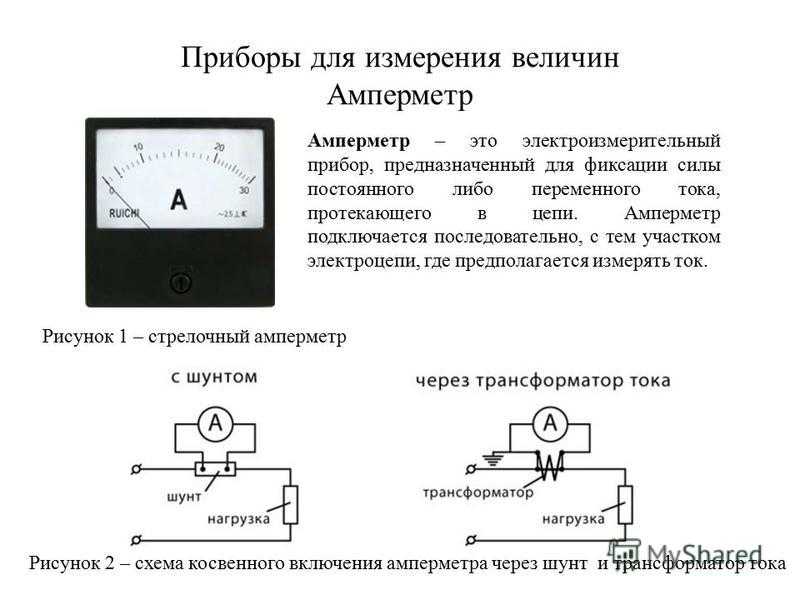 Его легко узнать, так как буква «А», заключенная в круг, изображенный на рисунке 2 ниже, обозначает амперметр.
Рис. 2 – Символ амперметра.
Иногда буква может иметь волнистую линию или прямую линию с пунктирной линией над ней. Это просто указывает, является ли ток переменным (переменный ток) или постоянным (постоянный ток) соответственно.
Формула и функции амперметра
Основная формула, которую следует учитывать при работе с амперметрами, это Закон Ома:
\[I=\frac{V}{R},\]
где $I$ ток в амперах ($\mathrm{A}$), $V$ – напряжение в вольтах ($\mathrm{V}$), а $R$ – сопротивление в омах (\ (\Омега\)). Если мы измерим ток с помощью амперметра, а напряжение — с помощью вольтметра, то сможем рассчитать сопротивление в определенной точке цепи.
Точно так же, если мы знаем сопротивление и напряжение цепи, мы можем перепроверить измерения нашего амперметра. Важно применить правильное уравнение для расчета сопротивления цепи. Амперметр всегда подключают последовательно, а вольтметр — параллельно. Напомним, что:
Если резисторы находятся в ряду (т. е. рядом друг с другом), вы складываете значение каждого резистора вместе: \[R_\mathrm{series}=\sum_{n}R_n=R_1 +R_2+ \cdots,\]
Если резисторы находятся в параллельно , правило для нахождения общего сопротивления выглядит следующим образом: \[\frac{1}{R_\mathrm{parallel}}=\sum_{n}\frac{1} {R_n} =\frac{1}{R_1}+\frac{1}{R_2}+\cdots.\]
Применим эти уравнения к примерной задаче, сравнивая ток в цепи с идеальным амперметром. по сравнению с неидеальным!
Последовательная цепь имеет два резистора, $1\,\Omega$ и $2\,\Omega$ соответственно, и батарею $12\,\mathrm{V}$. Чему равен измеренный ток этой цепи, если к ней подключен идеальный амперметр? Как изменится этот ток, если вместо него подключить неидеальный амперметр с внутренним сопротивлением $3\,\Омега$?
Рис. 3 – Принципиальная электрическая схема с последовательно включенным амперметром.
Ответ:
Сначала рассмотрим идеальные корпуса амперметров. Как следует из названия, в этом случае амперметр не имеет сопротивления, поэтому мы используем следующее уравнение, чтобы найти полное сопротивление этой последовательной цепи:
\begin{align} R_\mathrm{series}&=R_1+R_2 \ \ &= 1\,\Омега + 2\,\Омега\\ &=3\,\Омега. \end{align}
Мы можем использовать закон Ома
\[I=\frac{V}{R}\]
для расчета тока, который должен определять амперметр:
\[I=\frac{12\,\mathrm{V}}{3\,\ Omega}=4\,\mathrm{A}.\]
Теперь давайте проделаем те же шаги, только на этот раз с учетом внутреннего сопротивления амперметра:
\begin{align} R_\mathrm{series}& =R_1+R_2+ R_\mathrm{A}\\ &= 1\,\Омега + 2\,\Омега+3\,\Омега\\ &=6\,\Омега. \end{align}
Следовательно, ток, измеренный неидеальным амперметром, равен
\[I=\frac{12\,\mathrm{V}}{6\,\Omega}=2\,\mathrm{A}\]
, что в два раза меньше, чем у идеального амперметра.
На основании этих результатов можно сделать вывод, что внутреннее сопротивление амперметра может оказать существенное влияние на измерение фактического тока, протекающего по цепи.
Функция амперметра
Основная функция амперметра — измерение силы тока в электрической цепи. Итак, давайте пройдемся по основным этапам применения амперметра в цепи в реальной жизни. Пример схемы типичного амперметра показан на рисунке 4 ниже. Он имеет шкалу, отображающую диапазон токов, которые он сможет обнаружить, а также положительный и отрицательный разъемы, указанные на его основании. Иногда есть две шкалы, накладывающиеся друг на друга, каждая из которых будет иметь отдельный положительный разъем. Обычно они состоят из более широкого и узкого диапазона измерений, например, от $-1$ до $3$ и от $-0,2$ до $0,6$, изображенных на рисунке 1, что позволяет нам принять более точные измерения в этом меньшем диапазоне.
Рис. 4 – Схема амперметра.
В простой цепи, состоящей из батареи, источника (например, лампочки) и проводов, мы можем измерить ток, отсоединив провод от источника и батареи и вставив амперметр внутрь цепи.
Отрицательный разъем амперметра следует соединить с отрицательным выводом аккумулятора. Точно так же положительный разъем соединяется с положительным контактом . Осталось только прочитать измерение тока и оценить погрешность!
Влияние температуры
Из-за чувствительности амперметра при проведении измерений следует проявлять осторожность в отношении температуры окружающей среды. Колебания температуры могут привести к ложным показаниям. Например, если температура увеличивается, сопротивление увеличивается. Большее сопротивление означает, что через него будет протекать меньший ток; поэтому показания амперметра также будут ниже. Этот эффект можно уменьшить, подключив сопротивление заболачиванию к амперметру последовательно.
Сопротивление заболачиванию — сопротивление с нулевым температурным коэффициентом.
Амперметры
Эта статья посвящена, в частности, амперметрам. Однако в настоящее время существуют и другие приборы, используемые для измерения тока в электрической системе.
Например, для измерения силы тока обычно используется мультиметр .
Мультиметр — это инструмент, который измеряет электрический ток, напряжение и сопротивление в нескольких диапазонах значений.
Рис. 5. Мультиметр выполняет функции амперметра, вольтметра и омметра.
Как следует из определения, это очень универсальный инструмент, который может предоставить нам много информации о конкретной схеме. Вместо того, чтобы брать с собой амперметр, вольтметр и омметр, все это объединено в одном приборе.
Другим прибором, аналогичным амперметру, является гальванометр .
Гальванометр — это инструмент, используемый для измерения малых электрических токов.
Основное различие между двумя инструментами заключается в том, что амперметр измеряет только величину тока, а гальванометр также может определять направление.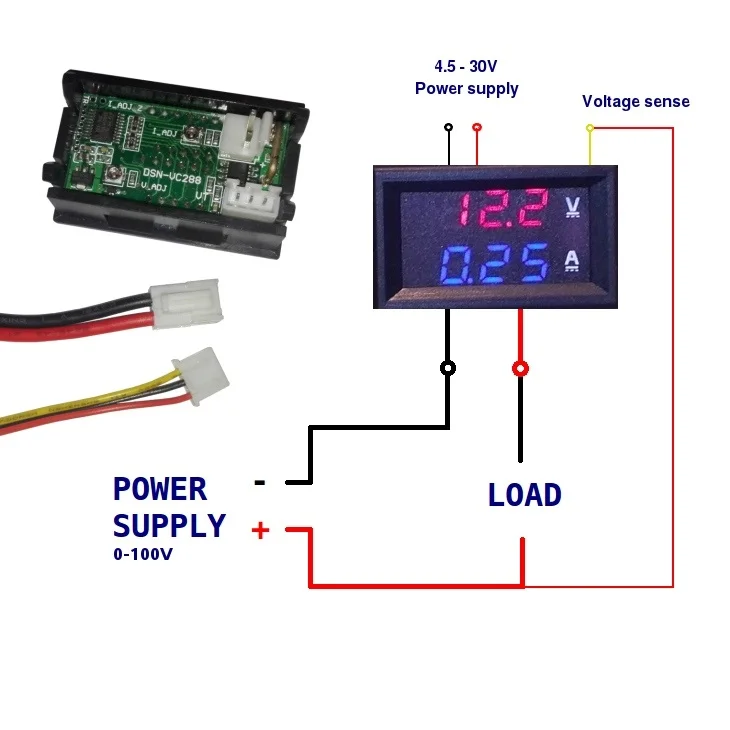 Однако он работает только для небольшого диапазона значений.
Преобразование гальванометра в амперметр
Гальванометр можно преобразовать в амперметр, просто добавив в цепь шунтирующее сопротивление $S$. Он имеет очень низкое сопротивление и должен быть подключен к гальванометру параллельно, как показано на рис. 6.9.0003
Рис. 6 – Шунтирующий резистор, подключенный параллельно гальванометру.
Мы знаем, что потенциальное сопротивление двух параллельных компонентов одинаково. Таким образом, применяя закон Ома, мы заключаем, что ток $I$ прямо пропорционален току, протекающему через гальванометр $I_\mathrm{G}$, исходя из следующего выражения:
\[I_\mathrm{ G}=\frac{S}{S + R_\mathrm{G}}I\]
, где $R_\mathrm{G}$ – сопротивление гальванометра.
Если мы хотим увеличить диапазон гальванометра, мы применяем
\[S=\frac{G}{n-1},\]
где $S$ – сопротивление шунта, $G\ ) — сопротивление гальванометра, а \(n$ — во сколько раз увеличивается сопротивление.
Амперметр — основные выводы
Амперметр — это инструмент, используемый для измерения силы тока в определенной точке цепи.
Амперметр всегда должен подключаться последовательно с элементом, в котором измеряется ток, так как в этом случае ток остается постоянным.
Идеальный амперметр имеет нулевое сопротивление, то есть он не влияет на ток элемента, с которым он соединен последовательно.
Символом амперметра в электрической цепи является буква «А», заключенная в круг.
Основной формулой, которую следует учитывать при работе с амперметрами, является закон Ома $I=\frac{V}{R}$.
Мультиметр — это инструмент, который измеряет электрический ток, напряжение и сопротивление в нескольких диапазонах значений.
Каталожные номера
Рис. 1 — Амперметр (https://commons.wikimedia.org/wiki/File:%D0%90%D0%BC%D0%BF%D0%B5%D1%80%D0%BC%D0%B5% D1%82%D1%80_2.jpg) автора Желуденко Павло лицензирован CC BY 4.