RC-цепи, 5 самых распространенных и как просто их рассчитать
RC-цепь, такое частое явление радиоэлектроники. Понимание характера влияния на форму АЧХ и их предназначения во многом определяет правильность чтения электронной схемы. В статье собранны 5 основных RC-фильтров, приведены их АЧХ и упрощенные формулы расчета.
В ранние годы развития радиоэлектроники основным видом воздействие на АЧХ сигнала были LC — фильтры, т.е. фильтры состоящие из катушки индуктивности и конденсатора. Со временем им на смену пришла RC-цепь, которая была плотно взята в оборот радиоэлектроникой ввиду меньшей стоимости и габаритов.
Конечно, RC-цепь не могут полностью вытеснить LC собратьев. Например в фильтрах для АС предпочтительнее использование LC-фильтров. Но практически во всей остальной маломощной электронике главенствуют рассматриваемые RC-цепи. Например двойная RC-цепь в фильтре RIAA-корректора.
Упрощенные формулы
Далее вы увидите, что в формулах присутствует коэффициент
1 / (2⋅π⋅10-6) = 159154 ≈ 160000
1. Фильтр Низких Частот (ФНЧ) — он же интегратор:
ФНЧ — фильтр, пропускающий без изменения частоты ниже частоты среза (f0) и подавляющий частоты выше f0. На частоте среза имеет значение амплитуды в -3dB. Это фильтр первого порядка и крутизна среза составляет 6дБ/октаву. Чаще всего такие фильтры используются для отсечения высокочастотных помех и шумов.
Октавой называется такой интервал частот, у которого конечное значение частоты больше начального в два раза.
2. Фильтр Высоких Частот (ФВЧ) — он же дифференциатор
ФВЧ — фильтр, ослабляющий частоты ниже частоты среза(f0) и пропускающий без изменения частоты выше f0. Так же как и у приведенного выше ФНЧ, сигнал на частоте среза обладает амплитудой в -3дБ, а крутизна среза 6 дБ на октаву.
И ФНЧ и ФВЧ работают как делитель напряжения, в котором одно плечо представлено постоянным резистором, а второе конденсатором, имеющим частотную зависимость.
Такие фильтры часто применяются на выходах звуковых усилителей для отсечения инфранизких, которые могут повредить АС.
3. Избирательный фильтр
Такой фильтр выделяет определенную частоту или полосу частот за счет подавления других частот. По сути этот фильтр представляет из себя последовательное включение ФНЧ и ФВЧ. Соответственно при равенстве между собой емкостей и сопротивлений выделена будет определенная частота, а в обе стороны будет ослабление с крутизной 6 дБ/окт .
Но никто не мешает расширить полосу пропускания, если рассчитать каждую RC-цепь R1С1 и R2C2 для разных f0.
4. Т- образные фильтры
Т- образные фильтры это те же Г-образными фильтры ФНЧ и ФВЧ к которым добавляется еще один элемент. Но особенностью Т-образных фильтров является то, что по сравнению с Г-образными оказывают меньшее шунтирующее действие на цепи стоящие за фильтром.
5. Двойной Т-образный фильтр — пробка
Фильтр имеет бесконечное затухание (порядка 60дБ) которое возникает благодаря сложению двух сигналов имеющих на частоте среза разность фаз 1800. Применение такого фильтра весьма эффективно для устранения сигнала помехи, например сетевой наводки 50 или 60Гц
audiogeek.ru
Исследование ачх пассивных фильтров методические указания
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ТС
к лабораторной работе по дисциплине «Устройства приема и обработки радиосигналов в СПРС»
УФА. 2002
Составитель: А.И.Гулин
Исследование АЧХ пассивных фильтров с использованием математического пакета МАТLАВ: Методические указания к лабораторным работам по курсу «Устройства приема и обработки радиосигналов в системах подвижной радиосвязи» Уфимский государственный авиационный технический университет; составитель: А.И.Гулин. Уфа 2002, 13 с.
Рассмотрены основные характеристики фильтров различных аппроксимаций. Описано большинство видов пассивных фильтров, даны ориентировочные АЧХ фильтров первого и второго порядков.
Предназначены для студентов направления 201200 «Средства связи с подвижными объектами», а также могут быть полезны студентам других специальностей направления «Телекоммуникации».
Рецензент: Беспалов А. И.
Уфимский государственный авиационный технический университет, 2002.
Содержание
стр.
1. Теоретическая часть………………………………………………………………4
Назначение, классификация и принцип работы пассивных фильтров…….4
Описание RC-фильтров……………………………………………………….4
Описание LC-фильтров……………………………………………………….7
Сравнение пассивных фильтров с другими видами фильтров……………..9
Практическая часть………………………………………………………………11
Варианты заданий…………………………………………………………………12
Контрольные вопросы……………………………………………………………12
Список литературы……………………………………………………………….13
Теоретическая часть
1.1. Назначение, классификация и принцип работы пассивных фильтров.
Основное назначение фильтра состоит в том, чтобы исключить прохождение сигналов определенного диапазона частот и в то же время обеспечить передачу сигналов другого диапазона частот. Фильтры делятся на активные и пассивные. Активные фильтры представляют собой частотно-избирательный усилительный каскад. К пассивным фильтрам относятся RC- и LC-фильтры. Фильтры также можно классифицировать исходя из диапазона частот, которые они пропускают или подавляют. Существуют четыре типа фильтров:
1. Фильтр нижних частот, который пропускает все сигналы с частотой ниже некоторого заданного значения и подавляет сигналы более высоких частот.
2. Фильтр верхних частот, который пропускает все сигналы с частотой выше некоторого заданного значения и подавляет сигналы более низких частот.
3. Полосно-заграждающий фильтр (режекторный), который используется для подавления сигналов определенного диапазона частот, тогда как сигналы с частотами выше и ниже этого диапазона проходят беспрепятственно.
4. Полосно-пропускающий фильтр (полосовой), который пропускает сигналы заданной полосы частот и препятствует прохождению сигналов любых других частот.
1.2. Описание rc-фильтров.
Ф ильтрация
сигналов низких (звуковых) частот обычно
осуществляется с помощью фильтров на
основе сопротивления и емкости (RC).
Схема фильтра верхних частот и его
амплитудно-частотная характеристика
показаны на рис. 1.
ильтрация
сигналов низких (звуковых) частот обычно
осуществляется с помощью фильтров на
основе сопротивления и емкости (RC).
Схема фильтра верхних частот и его
амплитудно-частотная характеристика
показаны на рис. 1.
Рис. 1. Схема и амплитудно-частотная характеристика высокочастотного RC-фильтра.
В этой схеме входное напряжение прикладывается и к резистору, и к конденсатору. Выходное же напряжение снимается с сопротивления. При уменьшении частоты сигнала возрастает реактивное сопротивление конденсатора, а следовательно, и полное сопротивление цепи. Поскольку входное напряжение остается постоянным, то ток, протекающий через цепь уменьшается. Таким образом, снижается и ток через активное сопротивление, что приводит к уменьшению падения напряжения на нем.
Фильтр характеризуется затуханием, выраженным в децибелах, которое он обеспечивает на заданной частоте. RC-фильтры рассчитываются таким образом, чтобы на выбранной частоте среза коэффициент передачи снижался приблизительно на 3 дБ (т.е. составлял 0,707 входного значения сигнала). Частота среза фильтра по уровню – 3 дБ определяется по формуле:
Фильтр низких частот имеет аналогичную структуру, только емкость и сопротивление там меняются местами. Амплитудно-частотную характеристику такого фильтра можно представить как зеркальное отображение АЧХ предыдущего.
В этой цепи входное напряжение также прикладывается и к резистору, и к конденсатору, но выходное напряжение снимается с конденсатора. При увеличении частоты сигнала реактивное сопротивление конденсатора, а следовательно, и полное сопротивление уменьшаются. Однако, поскольку это полное сопротивление состоит из реактивного и фиксированного активного сопротивлений, его значение уменьшается не так быстро, как реактивное сопротивление. Следовательно, при увеличении частоты снижение реактивного сопротивления (относительно полного сопротивления) приводит к уменьшению выходного напряжения. Частота среза этого фильтра по уровню -3 дБ также определяется по формуле предыдущего фильтра.
Рассмотренные выше фильтры представляют собой RC-цепи, которые характеризуются тремя параметрами, а именно: активным, реактивным и полным сопротивлениями. Обеспечиваемая этими RC-фильтрами величина затухания зависит от отношения активного или реактивного сопротивления к полному сопротивлению.
При расчете любого RC-фильтра можно задать номинал либо резистора, либо конденсатора и вычислить значение другого элемента фильтра на заданной частоте среза. При практических расчетах обычно задают номинал сопротивления, поскольку он выбирается на основании других требований. Например, сопротивление фильтра является его выходным или входным полным сопротивлением.
Соединяя фильтры верхних и нижних частот, можно создать полосовой RC-фильтр, схема и амплитудно-частотная характеристика которого приведены на рис. 2.
Р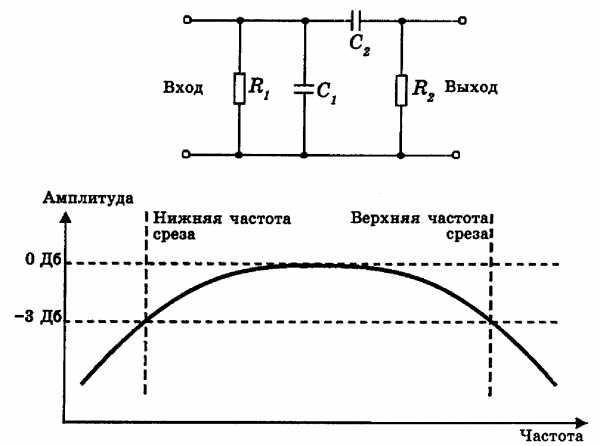 ис.
2. Схема и АЧХ полосовогоRC-фильтра.
ис.
2. Схема и АЧХ полосовогоRC-фильтра.
На схеме рис. 2.R1 – полное входное сопротивление; R2 – полное выходное сопротивление, а частоты низкочастотного и высокочастотного срезов определяются по формулам:
Следует отметить, что значение верхней частоты среза (fсв) должно быть по крайней мере быть в 10 раз больше нижней частоты среза (fсн), поскольку только в этом случае полосно-пропускающий фильтр будет работать достаточно эффективно.
Одиночный RC-фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области довольно часто используют многозвенные фильтры (рис. 3.). Частота среза многозвенного фильтра определяется по формуле ВЧ,НЧ RC-фильтра. Добавление каждого звена приводит к увеличению затухания на заданной частоте среза примерно на 6 дБ.
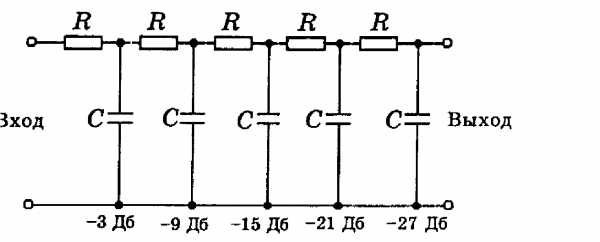
 Рис.
3. Многозвенные фильтры: соответственно
высокочастотный и низкочастотный.
Рис.
3. Многозвенные фильтры: соответственно
высокочастотный и низкочастотный.
studfile.net
Пассивные и активные режекторные фильтры. Онлайн расчёт.
Режекторный фильтр – не частый гость в наших краях. Зверь редкий, нелюдимый, но для радиолюбительского хозяйства – весьма полезный. Внешне напоминает полосовых собратьев, но охотится исключительно за сигналами вокруг центральной частоты и мало активен на частотах, выходящих за пределы отведённого ему диапазона.
Для начала определимся с терминологией.
Полосно-заграждающий фильтр (он же – режекторный фильтр, он же – фильтр-пробка) — электронный или любой другой фильтр,
не пропускающий сигналы со входа на выход в определённой полосе частот, но имеющий близкий к единице коэффициент передачи при
более низких и более высоких частотах.
Эта полоса подавления характеризуется шириной полосы заграждения и расположена вокруг центральной частоты подавления fо.
Заграждающий фильтр, предназначенный для подавления одной определённой частоты, называется узкополосным заграждающим фильтром
или фильтром-пробкой.
Для описания режекторных фильтров используют следующие параметры:
центральная частота подавления fо;
две граничных частоты – нижняя fн и верхняя fв, при которых Кu = 0,7mах;
диапазон частот Δf = fв − fн, называемый полосой задержания;
параметр Q = (fв + fн)/(2Δf), называемый добротностью.
Простейшие Т-образные фильтры и их амплитудно-частотная характеристика приведены на Рис.1.
Рис.1
Центральная частота подавления этих фильтров рассчитывается по формуле: fо = 1/(2π*R*C) при R1=R2=R, C1=C2=C. Глубина режекции – всего 10 дБ, а полоса задержания составляет значение, в 5-6 раз превышающее fо.
Именно в силу указанных выше хилых характеристик – подобные простейшие цепи уступили позиции двойным Т-образным RC-фильтрам (Рис.2), часто называемым 2ТФ.

Рис.2 Рис.3
Двойной Т-образный RC-фильтр при определённых условиях (симметрия моста, точный подбор элементов, согласование входа и выхода) почти полностью подавляет центральную частоту fo. Глубина режекции (подавления частоты fo) при работе на высокоомную нагрузку достигает 50 дБ. Добротность Q – около 0,3.
На Рис.2 приведена классическая схема двойного Т-образного режекторного фильтра, на Рис.3 – с возможностью плавной регулировки центральной частоты подавления.
Начнём с нерегулируемой схемы.
Обычно выбираются следующие соотношения элементов R2=R1, R3=R1/2.
Номиналы этих резисторов должны быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного
сопротивления последующего.
Ничего не изменилось, центральная частота вычисляется по формуле fо = 1/(2π*R*C).
РИСУЕМ ТАБЛИЦУ ДЛЯ ДВОЙНЫХ Т-ОБРАЗНЫХ RC-ФИЛЬТРОВ
При желании ввести регулировку центральной частоты подавления fо с диапазоном перекрытия по частоте более чем в 2 раза, при сохранении параметров, присущих двойным Т-образным режекторным фильтрам, имеет смысл воспользоваться схемой, приведённой на Рис.3.
Значение резистора R1 должно в 6 раз превышать суммарную величину R2, R3 и R4, поэтому его следует выбирать номиналом – не менее 100 кОм.
Формула для расчёта частоты подавления fо = 1/(2πС√3×R3_1×R3_2),
где R3_1 – сумма сопротивлений слева от регулирующего вывода R3, а R3_2 – справа.
Рисуем таблицу и для таких фильтров.
ТАБЛИЦА ДЛЯ ПЕРЕСТРАИВАЕМЫХ РЕЖЕКТОРНЫХ RC-ФИЛЬТРОВ
Дальнейшего улучшения параметров режекторных фильтров можно добиться введением в схему на Рис.2
положительной обратной связи, подаваемой в точки, идущие к земляной шине.
В результате подобных действий фильтры становятся активными и приобретают следующий вид.
Рис.4 Рис.5
На Рис.4 приведена схема активного режекторного фильтра на основе простого двойного Т-моста.
Значение добротности определяется отношением значений резисторов K=R5/R4. При изменении этого отношения в диапазоне К=0.01-0.2 добротность Q меняется практически линейно и принимает значения от 30 до 2. Дальнейшее увеличение параметра К не приветствуется, в связи с ухудшением неравномерности АЧХ в полосе пропускания.
Для желающих же регулировать значение добротности в более широких пределах на Рис.5 приведена схема активного режекторного фильтра на двух операционных усилителях. Здесь переменный резистор R4 позволяет изменять добротность в пределах 50 – 0.3.
А при необходимости получить перестраиваемый по частоте активный режекторный фильтр, регулирующий вывод переменного резистора R3 на Рис.3, точно таким же образом подключается к выходу операционного усилителя. Результатом является схема, изображённая на Рис.6 .
Рис.6 Рис.7
На Рис.7 приведена схема режекторного фильтра, позволяющая регулировать как частоту подавления, так и добротность в широких пределах.
Обе таблицы для расчёта частотозадающих элементов остаются в силе!
Ну, да и хватит, на следующей странице будем мурыжить режекторные LC фильтры.

vpayaem.ru
Расчет фильтров нижних и верхних частот
Практический расчет фильтров верхних и нижних частот (RC и LC фильтров)
Доброго дня уважаемые радиолюбители!
Сегодня, на сайте “Радиолюбитель”, на очередном занятии “Практикума начинающего радиолюбителя”, мы с вами рассмотрим порядок расчета фильтров верхних и нижних частот.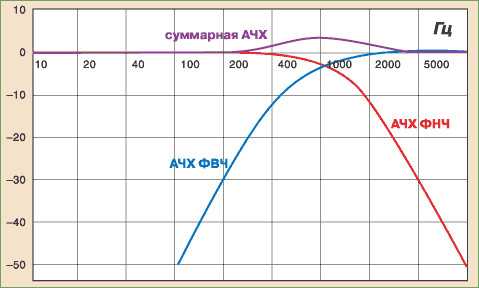 Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).
Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).
В первую очередь определимся, что понятия “верхние” и “нижние” частоты относятся к звукотехнике, а понятия “высокие” и “низкие” частоты – относятся к радиотехнике.
Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и служат для разных целей. Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный.
Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ). Что это за показатель.
АЧХ фильтра показывает как изменяется уровень амплитуду сигнала проходящего через этот фильтр в зависимости от частоты сигнала.
Т.е., на одной частоте входящего на фильтр сигнала уровень амплитуды такой-же как и на выходе, а для другой частоты, фильтр, оказывая сопротивление сигналу, ослабляет амплитуду входящего сигнала.
Тут же появляется еще одно определение: частота среза.
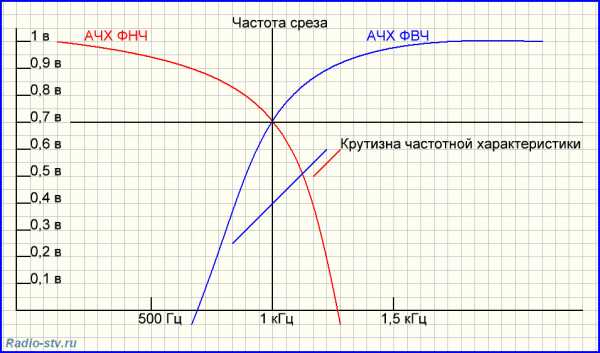
Частота среза – это частота, на которой происходит спад амплитуды выходного сигнала до значения равного 0,7 от входного.
Например, если при частоте входного сигнала 1 кГц амплитудой 1 вольт на выходе фильтра амплитуда входного сигнала уменьшается до 0,7 вольта, то частота 1 кГц является частотой среза данного фильтра.
И последнее определение – крутизна частотной характеристики фильтра.
Крутизна частотной характеристики фильтра – это показатель того, на сколько резко изменяется амплитуда входного сигнала на выходе при изменении его частоты. Чем быстрее происходит спад АЧХ тем лучше.
Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах.
Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала. Такое сопротивление называется реактивным и обозначается как Х.
Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:
Xc=1/2пFС где:
Хс – реактивное сопротивление конденсатора;
п – оно и в Африке “пи”;
F – частота;
С – емкость конденсатора.
То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.
А реактивное сопротивление катушки индуктивности вот этой формулой:
XL=2пFL где:
XL – реактивное сопротивление катушки индуктивности;
п – оно и в России “пи”;
F – частота сигнала;
L – индуктивность катушки
Частотные фильтры бывают нескольких типов:
– одноэлементные;
– Г- образные;
– Т – образные;
– П – образные;
– многозвенные.
В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов (фильтры с катушками индуктивности трогать не будем).
Одноэлементный фильтр
– фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот).
Г – образный фильтр
Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:

С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.
Формулы для расчета параметров делителя напряжения:
Uвх=Uвых*(R1+R2)/R2
Uвых=Uвх*R2/(R1+R2)
Rобщ=R1+R2
R1=Uвх*R2/Uвых – R2
R2=Uвых*Rобщ/Uвх
К примеру, нам дано:
Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 В
Порядок расчета:
1. Определяем R2= 7*10000/10= 7000= 7 кОм
2. Определяем R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм
3. Проверяем Uвых=10*7000/(3000+7000)= 7 В
Что нам и требовалось.
Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже.
ВАЖНО!
Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз.
Это правило также справедливо и при расчетах фильтров.
Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор.
Как вы уже знаете, конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально.
При замене сопротивления R1 на конденсатор (при этом на высоких частотах ток через него проходит беспрепятственно, а на низких ток через него не проходит) мы получим фильтр верхних частот.
А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот.
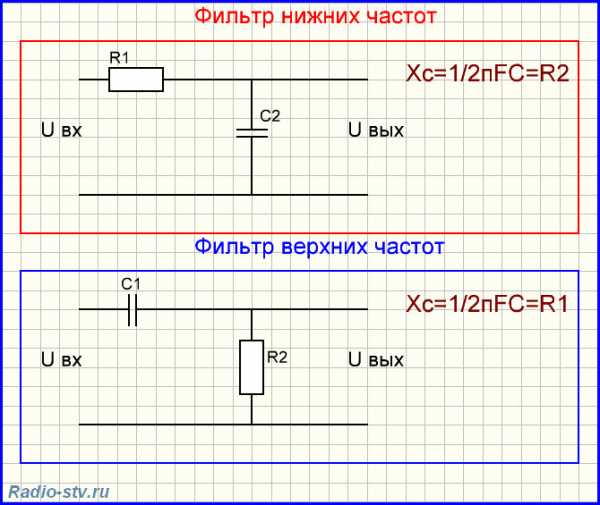
Как я уже сказал, уважаемые радиолюбители, мы не будем глубоко нырять в дебри электротехники, иначе мы заблудимся и забудем о чем шла речь. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему.
Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей.
Порядок расчета Г-образного фильтра верхней частоты
В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен. А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.
Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 —> C=1/2пFR1:
C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.
Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.
Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.
? Для справки:
? 1 мкФ = 10-6 Ф = 0,000 001 Ф
? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф
? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф
и так далее…
Порядок расчета Г-образного фильтра нижней частоты
Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 —> C=1/2пFR2:
C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.
Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.
Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.
Т – образный фильтр
Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:
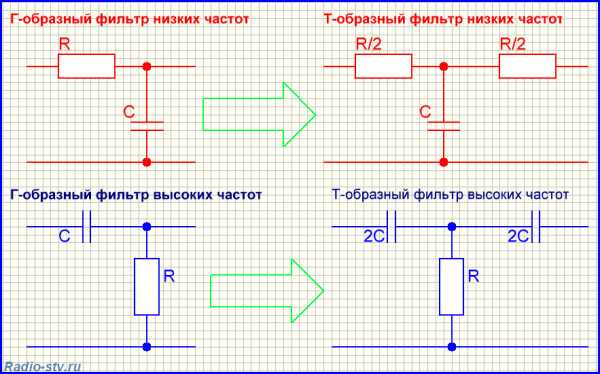
П – образный фильтр
П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных.
Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
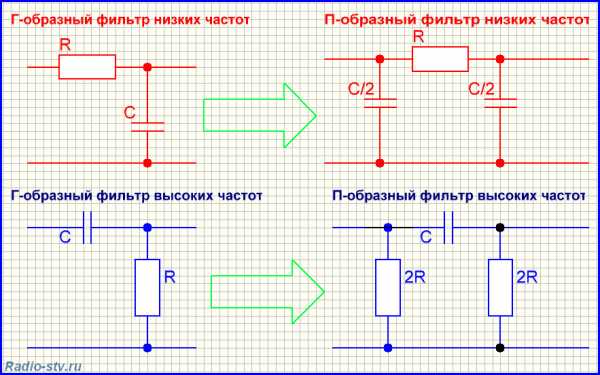
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.
Для написания статьи, кроме всего прочего использовались материалы с сайта www.meanders.ru, автором и владельцем которого является Александр Мельник, за что ему большое и бесконечное (меандровское) спасибо.
radio-stv.ru
6 Частотные rc-фильтры
Частотным фильтром называют радиотехническое устройство, которое обладает способность сравнительно легко пропускать переменные сигналы определенных частот и подавлять переменные сигналы, лежащие вне этих частот.
Фильтром высоких частот (ФВЧ) называют такой фильтр, который пропускает переменные сигналы высоких частот и подавляет сигналы низких частот.
Фильтром низких частот (ФНЧ) называют такой фильтр, который пропускает переменные сигналы низких частот и подавляет сигналы высоких частот.
Полосовым фильтром называют такой фильтр, который пропускает переменные сигналы только определенных частот и подавляет сигналы, имеющие частоты вне данных границ фильтра.
Заграждающим фильтром называют такой фильтр, который подавляет переменные сигналы только определенных частот и пропускает сигналы, имеющие частоты вне данных границ фильтра.
Любой фильтр
характеризуется комплексным коэффициентом
передачи 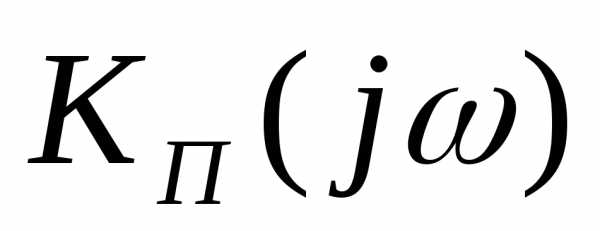 :
:
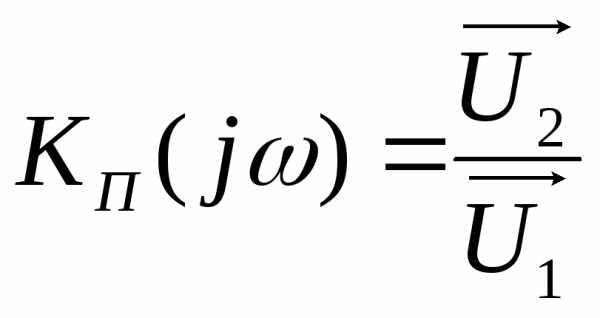 ,
(2.1)
,
(2.1)
где 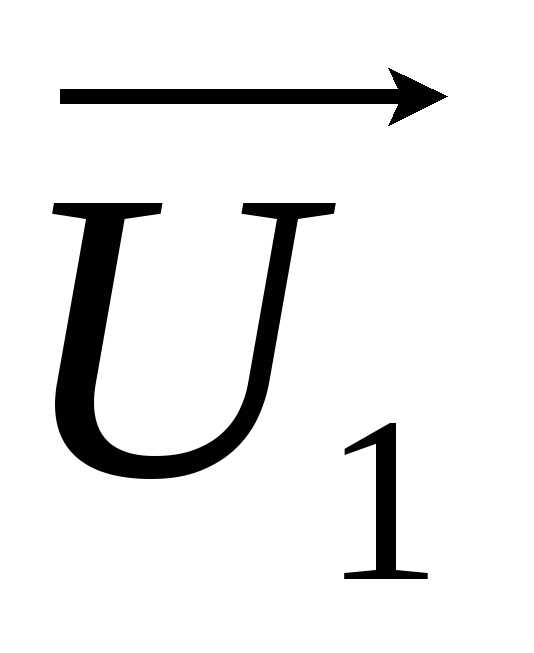 – вектор переменного напряжения на входе
фильтра;
– вектор переменного напряжения на входе
фильтра;
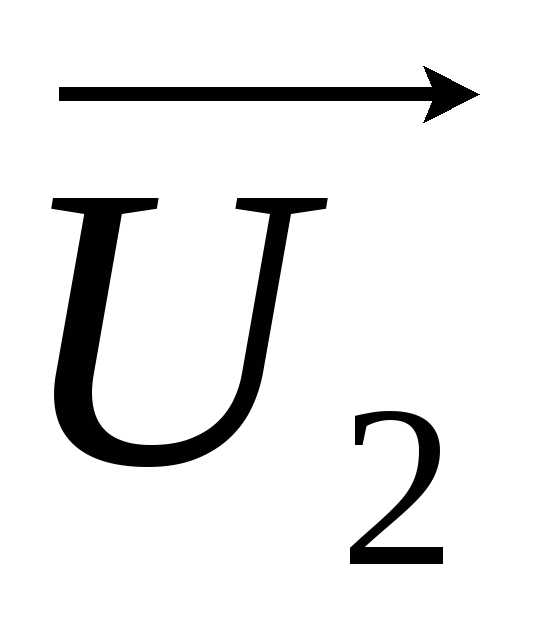 – вектор переменного
напряжения на выходе фильтра;
– вектор переменного
напряжения на выходе фильтра;
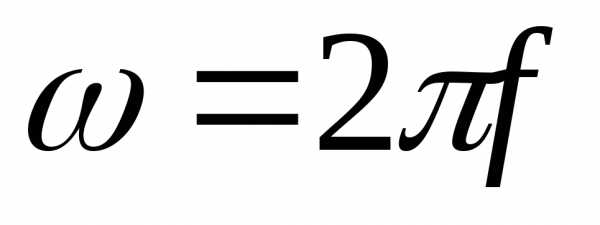 –
угловая частота переменного сигнала.
–
угловая частота переменного сигнала.
Комплексный коэффициент передачи представляет собой запись двух характеристик: амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ):
, (2.2)
Первая характеристика
выражается модулем комплексного
коэффициента передачи 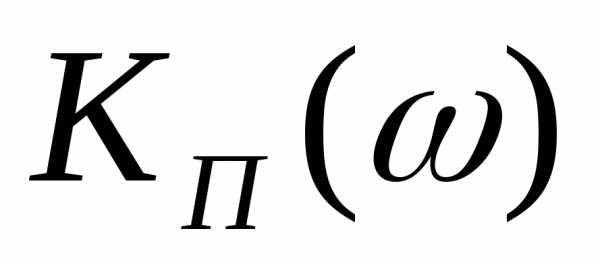 ,
а вторая – его аргументом
,
а вторая – его аргументом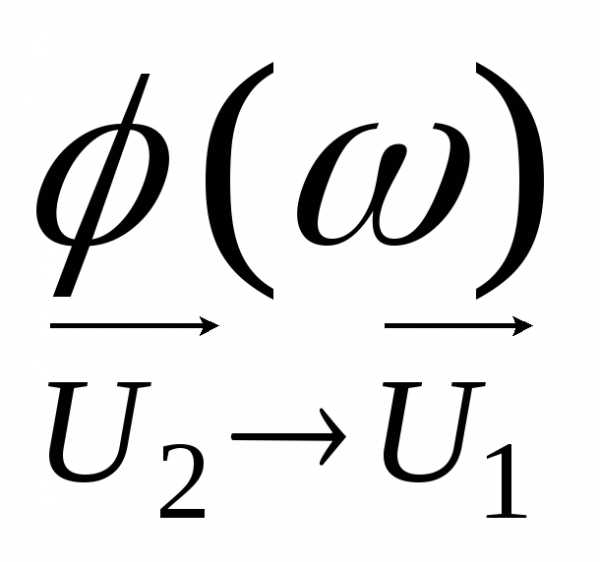 :
:
 , (2.3)
, (2.3)

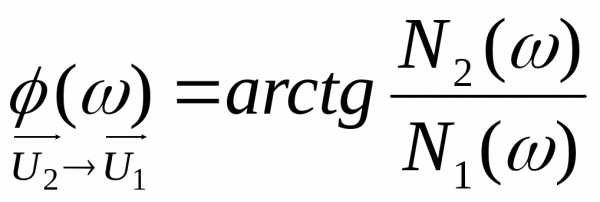 .
(2.4)
.
(2.4)
Обозначение  следует читать как сдвиг фаз величины
следует читать как сдвиг фаз величины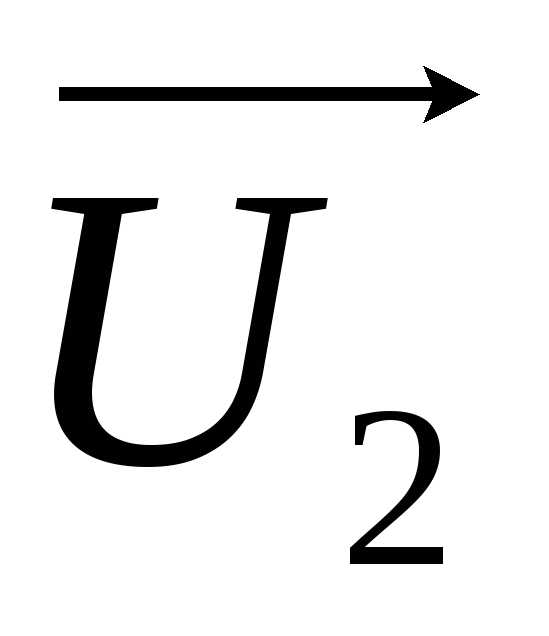 относительно величины
относительно величины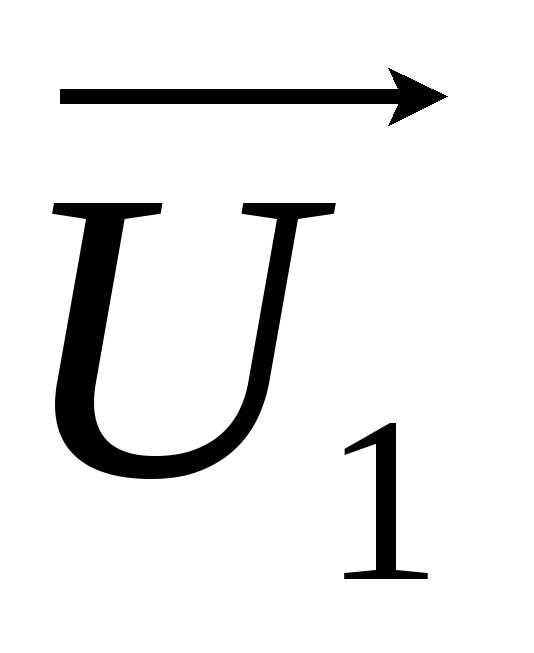 .
.
Если изменения амплитуд входного и выходного сигналов большие, то АЧХ выражают в логарифмическом масштабе. С этой целью вводится логарифмическая единица измерения модуля комплексного коэффициента передачи – децибел, которая определяется равенством:
 , (2.5)
, (2.5)
где 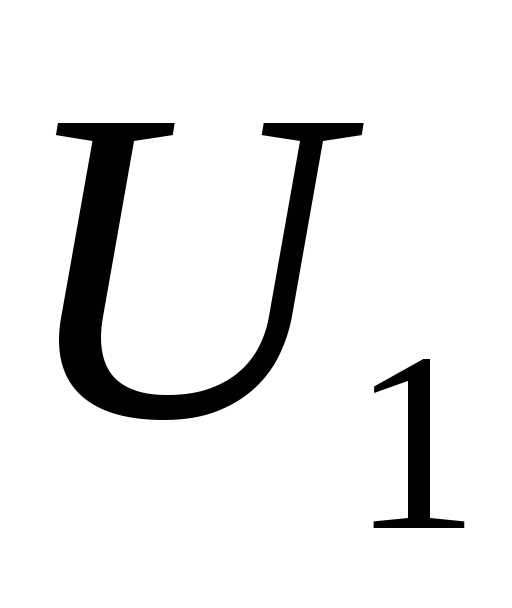 и
и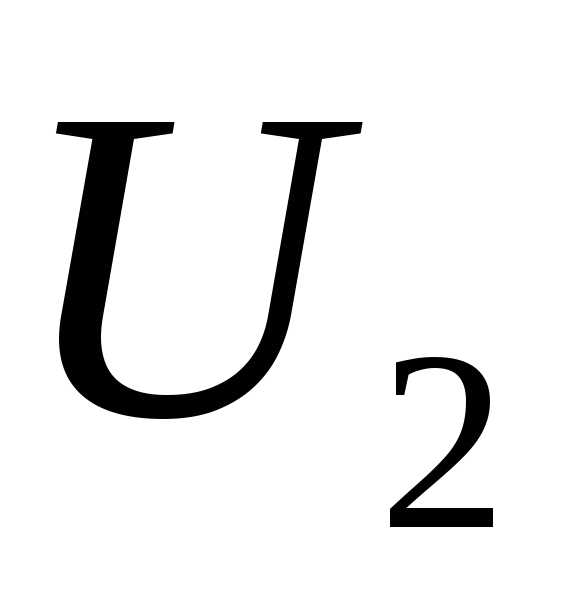 − амплитудные значения входного и
выходного напряжения.
− амплитудные значения входного и
выходного напряжения.
6.1 Rc-фильтр высоких частот
Схема RC-фильтра высоких частот приведена на рис.2.4 а.
Комплексный коэффициент передачи такого фильтра равен:
. (2.6)
Амплитудно-частотная характеристика (АЧХ) имеет вид:
. (2.7)
Фазочастотная характеристика (ФЧХ) имеет вид:

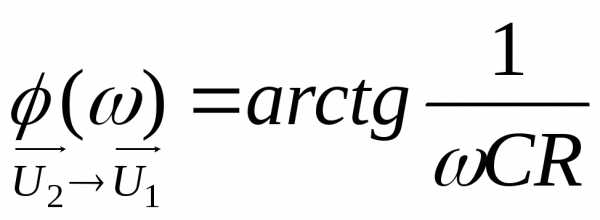 .
(2.8)
.
(2.8)
И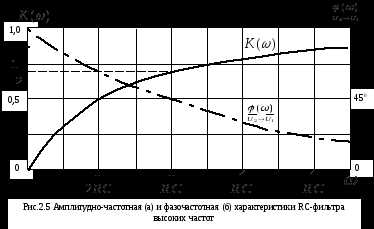 з
векторной диаграммы (рис.2.4 б) следует,
что выходной сигнал опережает входной
сигнал на угол
з
векторной диаграммы (рис.2.4 б) следует,
что выходной сигнал опережает входной
сигнал на угол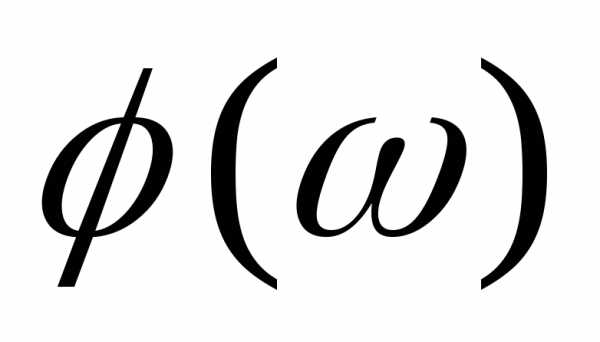 .
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.5. При частоте сигнала равной
.
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.5. При частоте сигнала равной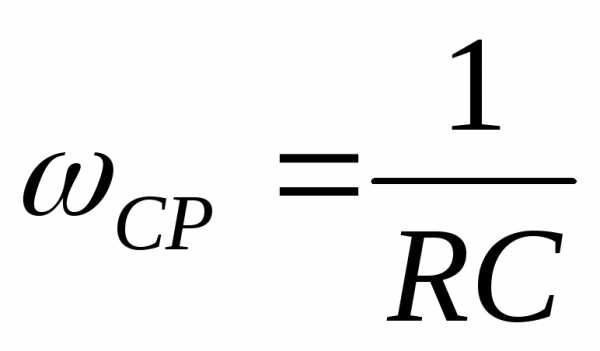 амплитуда сигнала уменьшается на –3дБ,
т.е. в
амплитуда сигнала уменьшается на –3дБ,
т.е. в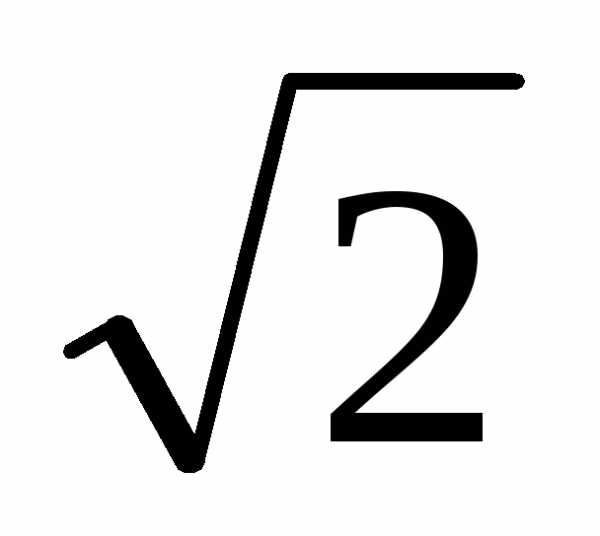 раз, а выходной сигнал опережает входной
сигнал на 450.
Такая частота называется частотой среза
фильтра.
раз, а выходной сигнал опережает входной
сигнал на 450.
Такая частота называется частотой среза
фильтра.
6.2 Rc-фильтр низких частот
Схема RC-фильтра низких частот приведена на рис.2.6 а.
Комплексный коэффициент передачи такого фильтра равен:
(2.9)
Амплитудно-частотная характеристика (АЧХ) имеет вид:
. (2.10)
Фазочастотная характеристика (ФЧХ) имеет вид:
 .
(2.11)
.
(2.11)
Из
векторной диаграммы (рис.2.6 б) следует,
что выходной сигнал отстает от входного
сигнала на угол 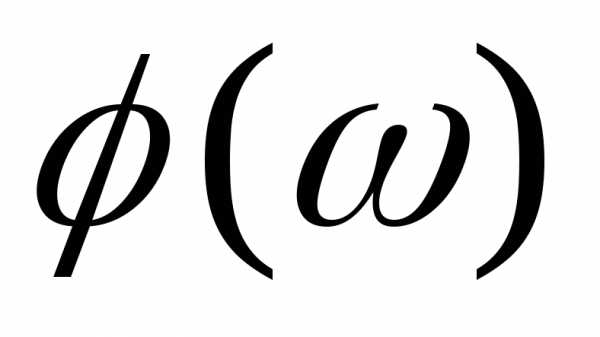 .
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.7. При частоте сигнала равной
.
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.7. При частоте сигнала равной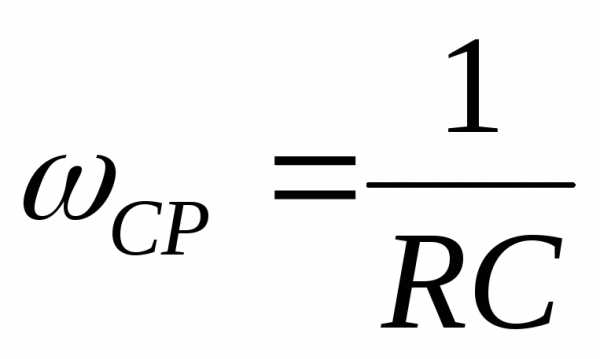 амплитуда сигнала уменьшается на –3дБ,
т.е. в
амплитуда сигнала уменьшается на –3дБ,
т.е. в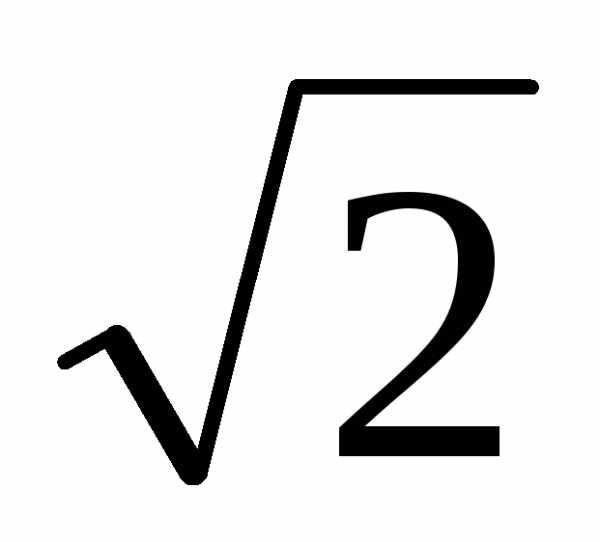 раз, а выходной сигнал отстает от входного
на 450.
Такая частота называется частотой среза
фильтра.
раз, а выходной сигнал отстает от входного
на 450.
Такая частота называется частотой среза
фильтра.

Контрольные вопросы
Приведите классификацию конденсаторов.
Назовите основные параметры конденсаторов.
Как обозначаются и маркируются постоянные конденсаторы?
Приведите основные конструкции постоянных конденсаторов.
Приведите определение частотных фильтров разного типа.
Приведите АЧХ и ФЧХ RC-фильтра высоких частот.
Приведите АЧХ и ФЧХ RC-фильтра низких частот.
Какие типы RC-фильтров вы знаете?
Л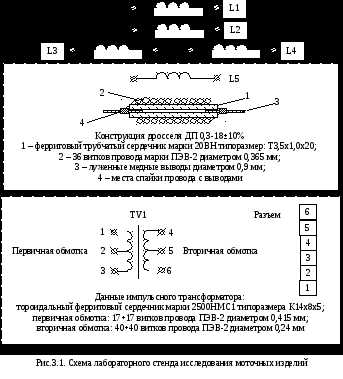 АБОРАТОРНАЯ
РАБОТА №3
АБОРАТОРНАЯ
РАБОТА №3
ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ВЫСОКОЧАСТОТНЫХ ДРОССЕЛЕЙ И ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ РЭА
Цель работы: ознакомление со свойствами, маркировкой и конструкцией основных типов высокочастотных дросселей и импульсных трансформаторов, а также с методикой их расчета.
Лабораторная схема
Схема лабораторного стенда приведена на рис.3.1. Она включает в себя 5 типов высокочастотных дросселей (L1- L5) и 1 импульсный трансформатор (VT1). Для исследования параметров импульсного трансформатора дополнительно используется испытательный стенд, схема которого приведена на рис.3.2.
Д омашнее
задание
омашнее
задание
Изучить основные параметры и маркировку дросселей и катушек индуктивности.
Изучить методику расчета дросселей и катушек индуктивности.
Подготовить протокол лабораторной работы, в котором начертить схему лабораторного стенда (рис.3.1 и 3.2).
Задание к лабораторной работе
Изучите маркировку, нанесенную на корпусе дросселей L1, L2 и катушек индуктивности L3, L4. Для этого:
1.1 Срисуйте маркировку, нанесенную на корпусе дросселей L1 – L4.
1.2 Расшифруйте номинальную индуктивность, рабочий ток, допуск, а также дополнительные сведения, обозначенные в маркировке на корпусе дросселей и катушек индуктивности.
1.3 Замерьте измерителем индуктивности значение индуктивности дросселей L1 − L4.
1.4 Определите отклонение замеренной индуктивности от номинального значения и сравните с допуском данного изделия.
1.5 Полученные данные занесите в таблицу 3.1.
Таблица 3.1 – Параметры исследуемых дросселей и катушек индуктивности
Обо-зна-че-ние | Маркировка на корпусе изделия | Из маркировки | Из эксперимента | Рабочий ток, мА | Примечание | ||
LНОМ, мГн | ΔLНОМ, % | LИЗМ, мГн | ,% | ||||
L1 | |||||||
L2 | |||||||
L3 | |||||||
L4 | |||||||
Рассчитайте параметры дросселя L5. Для этого:
Используя выражения (3.6) и конструктивные параметры дросселя, приведенные на рис.3.1, рассчитайте значение индуктивности дросселя.
Используя выражение (3.11), по диаметру используемого провода рассчитайте максимально допустимое значение рабочего тока, приняв допустимую плотность тока через провод равной 4 А/мм2.
Замерьте измерителем индуктивности значение индуктивности дросселя L5 и сравните с рассчитанным значением. Определите ошибку расчета в %.
Определите предполагаемые параметры импульсного трансформатора. Для этого:
Замерьте измерителем индуктивности значение индуктивности обмоток трансформатора L1-3 и L4-6 между контактами 1−3 и 4−6 разъема, соответственно.
Найдите коэффициент трансформации из замеренных значений индуктивности обмоток L1-3 и L4-6:
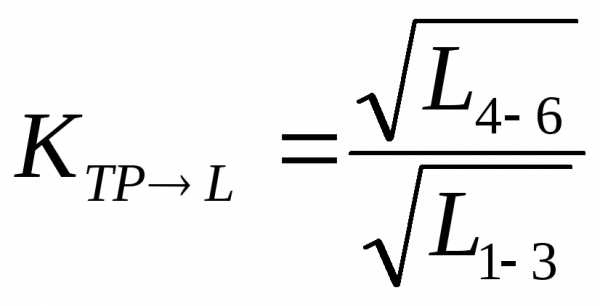 .
(3.1)
.
(3.1)
Используя выражения (3.10), по замеренному значению индуктивности L1-3 рассчитайте число витков w1-3 первичной обмотки. По рассчитанному значению коэффициента трансформации и рассчитанному числу витков w1-3 первичной обмотки рассчитайте число витков w4-6 вторичной обмотки трансформатора.
Сравните полученные значения w1-3 и w4-6 c паспортными данными трансформатора. Определите ошибку расчета числа витков в %.
Определите истинные параметры трансформатора. Для этого:
Вставьте плату с образцами в испытательный стенд.
Снимите зависимость выходного напряжения от выходного тока (нагрузочную кривую трансформатора) . Для этого к испытательному стенду к гнездам «U4-6 » подключите вольтметр.
Тумблер «U4-6/I4-6» поставьте в положение «U4-6». Измерьте напряжение холостого хода на вторичной обмотке трансформатора U4-6. Результаты измерения занесите в таблицу 3.2.
Тумблер «U4-6/I4-6» поставьте в положение «I4-6». Измерьте ток вторичной обмотке трансформатора I4-6. Результаты измерения занесите в таблицу 3.2.
Таблица 3.2. – Экспериментальные результаты исследования трансформатора
Условия | I4-6, мА | U4-6, В | I1-3, мА | U1-3, В | Р4-6, Вт | Р1-3, Вт | КТР | К.п.д., % |
Кнопки отжаты | ||||||||
Нажата кнопка Кн1 | ||||||||
Нажата кнопка Кн2 | ||||||||
Нажата кнопка Кн3 | ||||||||
Нажата кнопка Кн4 | ||||||||
Нажата кнопка Кн5 | ||||||||
Нажата кнопка Кн6 | ||||||||
Нажата кнопка Кн7 |
Повторите п.4.2.1-4.2.2 для семи различных нагрузок, последовательно нажимая кнопки 1…7. Результаты измерения занесите в таблицу 3.2.
Снимите зависимость тока потребления I1-3 и входного напряжения трансформатора
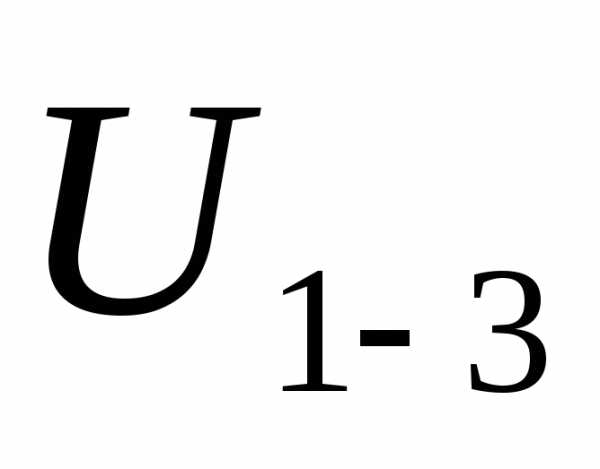 от тока нагрузки:
.
Для этого к испытательному стенду к
гнездам «U1-3»
подключите вольтметр.
от тока нагрузки:
.
Для этого к испытательному стенду к
гнездам «U1-3»
подключите вольтметр.Тумблер «U1-3/I1-3» поставьте в положение «U1-3». Измерьте напряжение на первичной обмотке трансформатора U1-3. Тумблер «U1-3/I1-3» поставьте в положение «I1-3». Измерьте ток первичной обмотке трансформатора I1-3. Результаты измерения занесите в таблицу 3.2.
Повторите п.4.3.1 для семи различных нагрузок последовательно нажимая кнопки 1…7. Результаты измерения занесите в таблицу 3.2.
Рассчитайте мощность трансформатора по вторичной обмотке для каждой точки измерения
(3.2)
Результаты измерения занесите в таблицу 3.2.
Рассчитайте потребляемую мощность трансформатора
(3.3)
Результаты измерения занесите в таблицу 3.2.
Определите к.п.д. трансформатора:
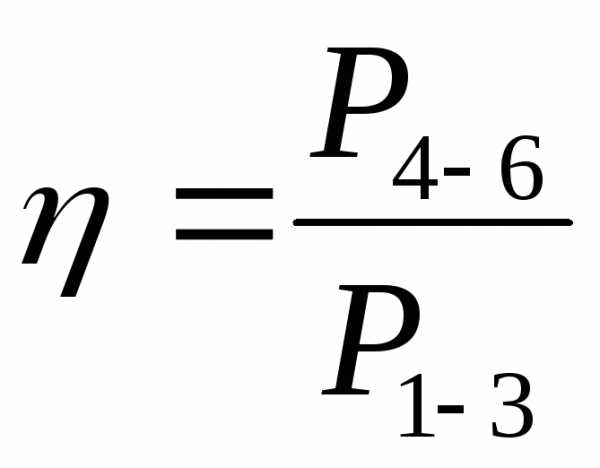 (3.4)
(3.4)
Результаты измерения занесите в таблицу 3.2.
Определите коэффициент трансформации по напряжению:
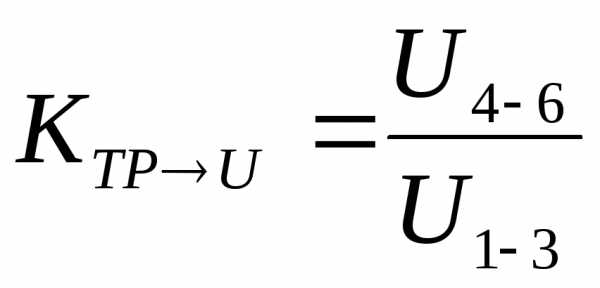 .
(3.5)
.
(3.5)
Результаты измерения занесите в таблицу 3.2.
Постройте график нагрузочной кривой трансформатора .
Постройте график зависимости к.п.д. трансформатора от тока нагрузки .
По графикам (см. рис.3.6) определите основные параметры трансформатора:
Определите номинальное выходное напряжение.
Определите максимальный выходной ток при снижении выходного напряжения на 20 %.
Определите коэффициент трансформации по напряжению при номинальной нагрузке и сравните его с коэффициентом, рассчитанным по (3.1).
Определите максимальную мощность трансформатора по вторичной обмотке.
Определите максимальное значение к.п.д. трансформатора.
Сделайте выводы по работе, в которых осветите применение исследуемых типов моточных изделий.
studfile.net
1.19. RC-фильтры
ОСНОВЫ ЭЛЕКТРОНИКИ
Полное и реактивное сопротивление
Благодаря тому что импеданс конденсатора, равный Zc = -j/ωС, зависит от частоты, с помощью конденсаторов и резисторов можно строить частотно-зависимые делители напряжения, которые будут пропускать только сигналы нужной частоты, а все остальные подавлять. В этом разделе вы познакомитесь с примерами простейших RС-фильтров, к которым мы будем неоднократно обращаться в дальнейшем. В гл. 5 описаны более сложные фильтры.
Рис. 1.52. Фильтр высоких частот.
Фильтры высоких частот. На рис. 1.52 показан делитель напряжения, состоящий из конденсатора и резистора. Согласно закону Ома для комплексных величин,
I = Uвх/Zполн = Uвх/R – (j/ωC) = Uвх[R + j/ωC)]/R2 + 1/ω2C2.
(Окончательный результат получек после умножения числителя и знаменателя на комплексное число, сопряженное знаменателю.) Итак, напряжение на резисторе R равно
Uвых = IZR = IR = Uвх[R + (j/ωС)R]/R2+1/ω2C2.
Чаще всего нас интересует не фаза, а амплитуда Uвых:
Uвых = (UвыхUвых*)1/2 = UвхR/[R2 + (1/ω2C2)]1/2.
Сравните полученный результат с выражением для резистивного делителя:
Uвых = UвхR1/(R1 + R2).
Векторное представление импеданса RС – цепи (рис. 1.53) показано на рис. 1.54.

Рис. 1.53.

Рис. 1.54.
Итак, если не принимать во внимание сдвиг фаз, а рассматривать только модули комплексных амплитуд, то «отклик» схемы будет определяться следующим образом:
Uвых = UвхR/[R2 + (1/ω2C2)]1/2 = Uвх2πƒRC/[1 + (2πƒRC)]1/2.
График этой зависимости представлен на рис. 1.55. Такой же результат мы бы получили, если бы определили отношение модулей импедансов как в упражнении 1.17 и в примере перед этим упражнением; числитель представляет собой модуль импеданса нижнего плеча делителя R, а знаменатель – модуль импеданса последовательного соединения R и С.
Рис. 1.55. Частотная характеристика фильтра высоких частот.
Как вы видите, на высоких частотах выходное напряжение приблизительно равно входному (ω > 1/RC), а на низких частотах выходное напряжение уменьшается до нуля. Мы пришли к важному результату, запомните его. Подобная схема, по понятным причинам, называется фильтром высоких частот. На практике ее используют очень широко. Например, в осциллографе предусмотрена возможность связи по переменному току между исследуемой схемой и входом осциллографа. Эта связь обеспечивается с помощью фильтра высоких частот, имеющего перегиб характеристики в области 10 Гц (связь по переменному току используют для того, чтобы рассмотреть небольшой сигнал на фоне большого напряжения постоянного тока). Инженеры часто пользуются понятием «точки излома» -3 дБ для фильтра (или любой другой схемы, которая ведет себя как фильтр)! В случае простого RC – фильтра высоких частот точка излома -3 дБ определяется выражением:
ƒ3дб = 1/2πRC.
Обратите внимание, что конденсатор не пропускает ток (ƒ = 0). Самый распространенный пример использования конденсатора-это использование его в качестве блокирующего конденсатора постоянного тока. Если возникает необходимость обеспечить связь между усилителями, то почти всегда прибегают к помощи конденсатора. Например, у любого усилителя звуковой частоты высокого класса все входы имеют емкостную связь, так как заранее не известно, какой уровень постоянного тока будут иметь входные сигналы. Для обеспечения связи необходимо подобрать R и С таким образом, чтобы все нужные частоты (в данном случае 20 Гц – 20 кГц) поступали на вход без потерь (без деления на входе).
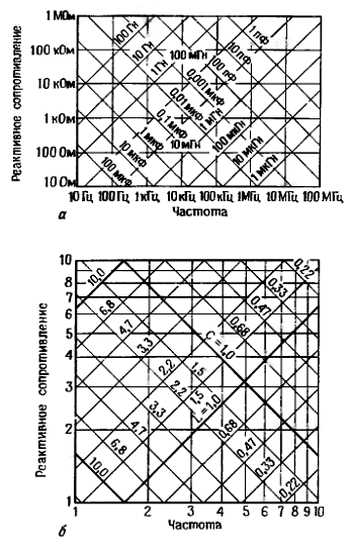
Рис. 1.56. а – Изменение реактивного сопротивления индуктивностей и конденсаторов в зависимости от частоты. Все декады одинаковы и отличаются лишь масштабом. б – Увеличенное изображение одной декады из графика А. график построен для стандартных компонентов, имеющих точность 20%.
В качестве примера рассмотрим фильтр, показанный на рис. 1.57. Это фильтр высоких частот с точкой перегиба 3 дБ на частоте 15,9 кГц. Импеданс нагрузки, подключаемой к фильтру, должен быть значительно больше 1 кОм. иначе нагрузка будет искажать выходное напряжение фильтра. Источник сигнала должен обеспечивать возможность подключения нагрузки 1 кОм без значительной аттенюапии (потери амплитуды сигнала), иначе фильтр будет искажать выход источника сигнала.
Рис. 1.57. Рис. 1.58. Фильтр низких частот.
Фильтры низких частот. Если поменять местами R и С (рис. 1.58), то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что Uвых = [1/1 + ω2R2С2)1/2] Uвх. График этой зависимости представлен на рис. 1.59. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC. Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио – и телевизионных станций (550 кГц – 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Рис. 1.59 Частотная характеристика фильтра низких частот.
Упражнение 1.21. Докажите справедливость выражения для выходного напряжения фильтра низких частот.
Выход фильтра низких частот можно рассматривать в качестве самостоятельного источника сигналов. При использовании идеального источника напряжения переменного тока (с нулевым импедансом) фильтр со стороны выхода низких частот имеет сопротивление R (при расчетах полных сопротивлений идеальный источник сигналов можно заменить коротким замыканием, т.е. его нулевым импедансом для малого сигнала). В выходном импедансе фильтра преобладает емкостная составляюшая. и на высоких частотах он становится равным нулю. Для входного сигнала фильтр представляет собой нагрузку, состоящую на низких частотах из сопротивления R и сопротивления нагрузки, а на высоких частотах – нагрузку, равную просто сопротивлению R.
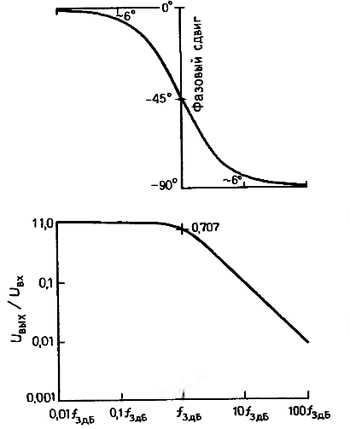
Рис. 1.60. Фазочастотная и амплитудно-частотная характеристики фильтра низких частот, изображенные в логарифмическом масштабе. В точке 3 дБ фазовый сдвиг составляет 45° и в пределах декады изменения частоты лежит в пределах 6° от асимптотическою значения.
На рис. 1.60 изображена также частотная характеристика фильтра низких частот, но в более общепринятом виде для вертикальной и горизонтальной осей использован логарифмический масштаб. Можно считать, что по вертикальной оси откладываются децибелы, а по горизонтальной – октавы (или декады). На таком графике равные расстояния соответствуют равным отношениям величин. В виде графика изображен также фазовый сдвиг, при этом для вертикальной оси (градусы) использован линейный масштаб, а для оси частот-логарифмический. Такой график удобен для анализа частотной характеристики даже в случае значительной аттенюации (справа): целый ряд таких графиков представлен в гл. 5, посвященной изучению активных фильтров. Отметим, что при значительной аттенюации изображенная на графике кривая вырождается в прямую линию с наклоном -20 дБ/декада (инженеры предпочитают выражение « -6 дБ/октава»). Отметим также, что фазовый сдвиг плавно изменяется от 0° (на частотах ниже точки перегиба) до 90° (на частотах существенно выше точки перегиба), а в точке -3 дБ составляет 45°. Практическое правило для односекционных RС – фильтров говорит о том. что фазовый сдвиг составляет ≈6° от асимптот в точках 0.1ƒ3дБ и 10ƒ3дБ.
Упражнение 1.22. Докажите последнее утверждение.
Возникает интересный вопрос: можно ли сделать фильтр с какой-либо другой заданной амплитудной характеристикой и какой-либо другой заданной фазовой характеристикой. Пусть вас это не удивляет, но ответить можно только отрицательно – нельзя. Фазовая и амплитудная характеристики для всех возможных фильтров подчиняются законам причинной связи (т.е. характеристика является следствием определенных свойств, но не их причиной).
Частотные характеристики дифференцирующих и интегрирующих RС – цепей. Схема дифференцирующей RС – цепи, которую мы рассмотрели в разд. 1.14, имеет такой же вид, как и схема фильтра высоких частот, приведенная в настоящем разделе. Чем же считать такую схему, зависит от того, что вас больше интересует: преобразование сигналов во времени или частотная характеристика. Полученное ранее временное условие правильной работы схемы (Uвых « Uвх) можно сформулировать иначе, применительно к частотной характеристике: для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен Uвх = sinωt. Воспользуемся уравнением, которое мы получили ранее для выхода дифференциатора:
Uвх = RC d/dt sinωt = ωRCcosωt.
Отсюда Uвых « Uвх, если ωRC « 1, т.е. RC « 1/ω. Если входной сигнал содержит некоторый диапазон частот, то условие должно выполняться для самых высоких частот входного диапазона.
Схема интегрирующей RC – цепи (разд. 1.15) имеет такой же вид, как и схема фильтра низких частот: аналогично в хорошем интеграторе самые низкие частоты входного сигнала должны существенно превышать частоту в точке -ЗдБ.
Индуктивности и конденсаторы. Индуктивности, также как и конденсаторы, в сочетании с резисторами образуют схемы фильтров низких (или высоких) частот. Однако на практике RL – фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС – фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель – это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Диоды и диодные схемы
skilldiagram.com
“Волшебные” свойства RC цепочки / Схемотехника / Сообщество EasyElectronics.ru
«Волшебные» свойства обычного ФНЧ — RC фильтра. В данном топике я расскажу, как можно использовать свойства данного типа пассивного фильтра не по прямому назначению. Иногда может быть полезнее, проще и «дешевле» использовать аналоговую схемотехнику, чем сложные программные реализации или другое более дорогостоящее оборудование.Предисловие.
Рассмотрим простейший аналоговый фильтр – RC цепочку или ФНЧ (фильтр низких частот). Про него написано много и по делу. Но мы попробуем использовать его свойства не по прямому назначению. Данный фильтр является пассивным ФНЧ 1-го порядка. Его характеристики для качественной фильтрации сигнала далеки от оптимальных. Но для рассматриваемого случая их хватит.
Не много формул
Вспомним основные характеристики RC цепи. Схема данного ФНЧ выглядит следующим образом.
Комплексный коэффициент передачи данного фильтра вычисляется по закону Ома и имеет следующий вид:
Значение силы тока в цепи равно:
Подставляя значение тока в первую формулу получим:
R- сопротивление резистора в цепочки, Zc – реактивное сопротивление конденсатора в цепи.
Где. Формула для передаточного коэффициента примет окончательный вид:
Так как коэффициент является мнимой функцией, то у нас возникает разность фаз между входным и выходным напряжением. Угол этого сдвига вычисляется по формуле:
Так как угол со знаком «минус», это означает что выходное напряжение отстает от входного на угол ⱷ.
Этим свойством фильтра мы и воспользуемся.
АЧХ и ФЧХ фильтра.
Вспомним две основные характеристики любого фильтра: АЧХ и ФЧХ. Вот АЧХ и ФЧХ RC цепочки:
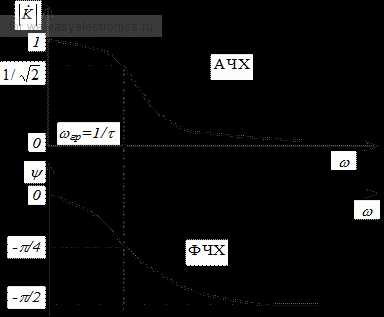
Вспомним тригонометрию и табличные значения тангенса:
Как видим тангенс 90° в таблице не указан, стоит прочерк. Это означает, что его нельзя вычислить.
Так что и в нашем пассивном фильтре отставание выходного напряжения от входного не может быть больше 90°, да и 90° получить не получится. 89,9° реально, а вот больше уже практически невозможно. Теперь основной вопрос. Зачем нам получать этот сдвиг в 89,9°?
Зачем городить все это?
Обрисуем задачу. Необходимо вычислять момент, создаваемый асинхронным высоковольтным двигателем. Не важно зачем он нам нужен, для того что бы знать механическую работу совершенную двигателем, или так для статистики. Необходимо и все тут. Практическое применение этого может возникнуть в разных областях промышленности. Давайте решим её. Тут правда придется вспомнить теорию электрических машин. Приступим.
Асинхронный электродвигатель.
Номинальный момент рассчитывается по формуле:
Где Pн – номинальная мощность на валу двигателя, nн — номинальная частота вращения ротора.
А как известно Pн есть не что иное, как Раст – Рпот. Мощность потерь складывается из потерь в обмотках, потерь в железе и механических потерь. Механические потери равны константе и зависит от типа двигателя. А вот потери в обмотках и железе динамические. Обмотки и железо греются, следовательно, возрастают и потери. Для больших мощностей этот параметр будет носить характер в 0.5 % или менее.
Теперь о расчете активной (полезной) мощности.
В трехфазной сети она вычисляется следующим образом:
Где ⱷ — угол между током и напряжением. Для симметричной нагрузки это справедливо, а исправный электродвигатель является симметричной нагрузкой.
Так вот для вычисления момента на валу, необходимо измерять две основные электрические величины: U и I. Фазное напряжение и ток. С током все понятно, ставим трансформатор тока и вперед. А вот с напряжением сложнее.
Не забудем, что разговор мы ведем о высоковольтном электродвигателе. Так что 6 кВ не подашь на схему измерения.
Решений как всегда может быть несколько.
- Поставить трансформатор напряжения фазный.
- Использовать свойства RC цепи при измерении линейного напряжения.
В высоковольтных ячейках, с которых осуществляется пуск двигателя, в своем составе уже имеют трансформаторы напряжения и тока, как для устройств защиты, так и для средств измерения.
Типовые схемы включения трансформаторов напряжения представлено ниже: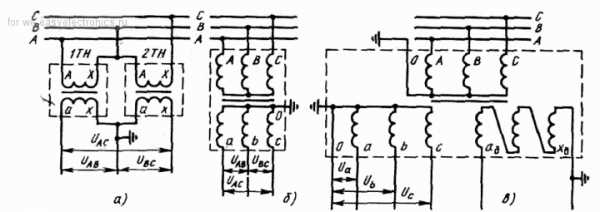
При чем вариант В применяется реже. В основном вариант А или Б. Как видно с трансформаторов мы снимаем линейное напряжение высоковольтной сети. А для расчета Активной мощности необходимо фазное. Ну и что, возразите ВЫ? Поделили на корень из 3 и вуаля!
Делением мы вычислим среднеквадратичное значение напряжения, но для вычисления активной мощности этого мало. Если мы умножим среднеквадратичные U*I, то получим ПОЛНУЮ мощность. А это не совсем то, совсем не то.
Применение свойств RC цепи.
Добрались до самой сути статьи.
Если обрабатывать сигналы тока и напряжения МК, что в современных реалиях считается обязательным. То мы придем к следующим формулам. Для среднеквадратичного напряжения:
Где К – коэффициент трансформации, N – количество замеров за период напряжения, u – мгновенные значения напряжения. Для тока все будет тоже самое. Для вычисления полной мощности остается умножить U*I*3 для трехфазной симметричной нагрузки. А как же быть с активной мощностью? Активная мощность может быть вычислена следующим образом:
Осталось только взять замеры тока и напряжения в одни и те же отрезки времени на протяжении периода, просуммировать их произведение.
Рассмотрим типовую схему включения трансформатора напряжения в ВВ ячеки. Это вариант А.
Трансформатор тока включен в фазу B. Посмотрим диаграмму напряжений в трехфазной сети.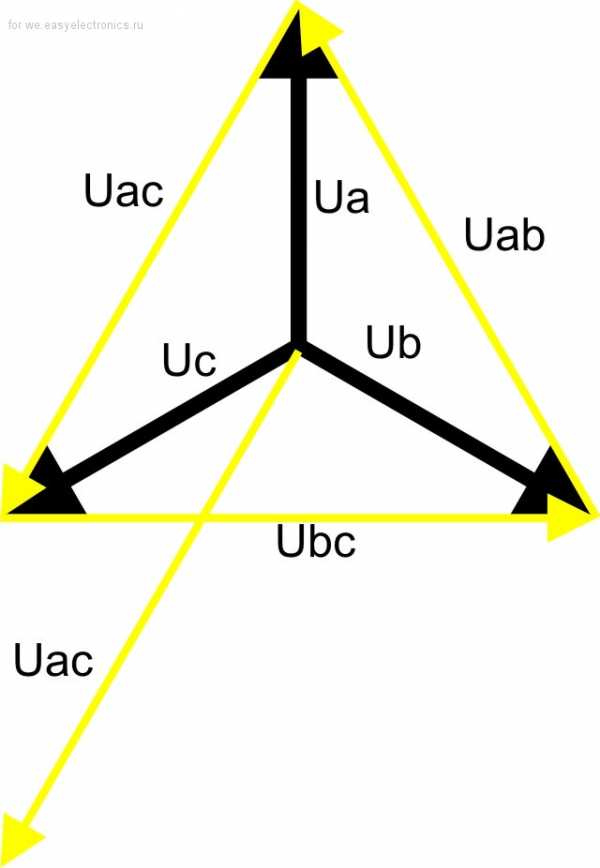
Фазное напряжение Ub и линейное напряжение Uac располагаются под углом в 90°. При чем напряжение Uac отстает от фазного напряжения Ub. Ничего не напоминает.
Правда, амплитуда линейного напряжения больше фазного в корень из 3 раз. Но на МК уменьшить коэффициент на эту величину не составляет труда.
Значит у нас два критерия для нашего фильтра. Сдвиг фазы выходного напряжения относительно входного должно составлять ≈90°. Коэффициент передачи на данной частоте, должно быть такой, чтобы обеспечить выходное напряжение после фильтра в пределах 1-1.5 вольта.
Приступим к вычислениям.
Расчет фильтра.
С трансформатора напряжения приходит 100 вольт напряжения (стандарт). Это действующее напряжение, следовательно, чтобы нам определить амплитудное значение умножим на корень из 2.
ИТОГО: Umax=U*1.41=141В.
Это синусоида, и она имеет как положительную полуволну, так и отрицательную. Значит, нам для МК необходимо эту синусоиду поднять в положительное напряжение.
Напряжение питание МК возьмем 3 в. Значит, средняя точка для синусоиды будет 1.5 вольта. Итого размах полуволны напряжения нам остается 1.5вольта. Отсюда коэффициент передачи RC цепи будет:
Теперь вычислим значение τ=RC, исходя из коэффициента К. Частота сигнала известна 50 Гц.
После математических преобразований получаем: τ=RC = 0,318
Отсюда
Угол нас устраивает. Вычислим погрешность измерений, при ошибки фазы в 0,57°, следовательно ошибка равна: (0,57°/90°)*100%=0,63%, это за четверть периода, следовательно за 360° и того меньше. Вряд ли трансформаторы тока и напряжения будут классом точности выше чем 0,5%. Так что, искажениями, вносимыми нашем фильтром можно пренебречь.
Осталось рассчитать сами значения R и C. Отталкиваться лучше от конденсатора. Возьмем С=4,7 мкФ, отсюда R= τ/С=0,318/4,7*10-6=318*10-3/4,7*10-6=67,66*103 Ом или 67,66 кОм.
Теперь подтвердим наши расчеты симулятором Proteus и посмотрим, отличается ли его математика от нашей.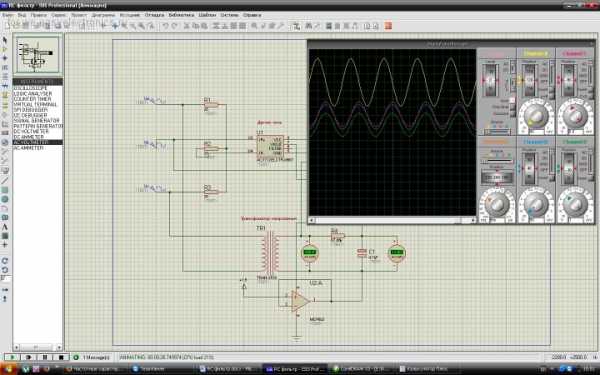
Проект протеуса прикладываю к статье. Можете убедиться, что расчеты верны.
Вот таким нехитрым способом можно заставить работать RC цепочку не по назначению.
ВИДЕО демонстрирующее возможности RC фильтра.
Применение в практике данного способа использования RC цепи я опишу в следующей раз.
UPD:
Пользователь Santik в комментариях затронул вопрос о реальных сетях, с присутствующими искажениями основной частоты 50 Гц гармониками. Было высказано предложение просимулировать в протеусе данную ситуацию. Схема протеуса конечно, не реальная картина на производстве, но показывает, что если сигнал основной частоты искажен гармониками небольшой амплитуды, то RC фильтр хорошо выделяет основную частоту и нормализует синус.Видео, демонстрирующее работу фильтра с сигналом, искаженным гармониками.
we.easyelectronics.ru


