Эдс индукция: что это такое, основные формулы, в чем измеряется, от чего зависит.

что это такое, основные формулы, в чем измеряется, от чего зависит.

В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.

Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.

Магнитный поток

Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.

При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.

ЭДС индукции

Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.

Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.

Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.

Законы Фарадея и Ленца

Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.

Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.

Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.

Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:

Е = — dФ/dt.

Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.

Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.

Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.

Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.

Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.

Движение провода в магнитном поле

Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.

Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.

Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.

Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.

Вращающаяся катушка

Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).

Согласно формуле, на Ф воздействуют изменения в ситуациях:

• при изменении магнитного потока меняется вектор направления;
• изменяется площадь, заключенная в контур;
• меняется угол.

Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.

На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.

ЭДС самоиндукции

При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.

В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:

Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.

Взаимоиндукция

При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.

Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.

Значение взаимоиндуктивности второй катушки в отношении первой:

М21 = (N2 x F21)/I1.

Значение магнитного потока:

Ф21 = (М21/N2) x I1.

Индуцированная ЭДС вычисляется по формуле:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt.

В первой катушке значение индуцируемой ЭДС:

Е1 = — M12 x dI2/dt.

Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.

Тогда взаимоиндуктивность считается равной:

М12 = М21 = М.

Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.

Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.

Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.

расчет электродвижущей силы по формуле

Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени.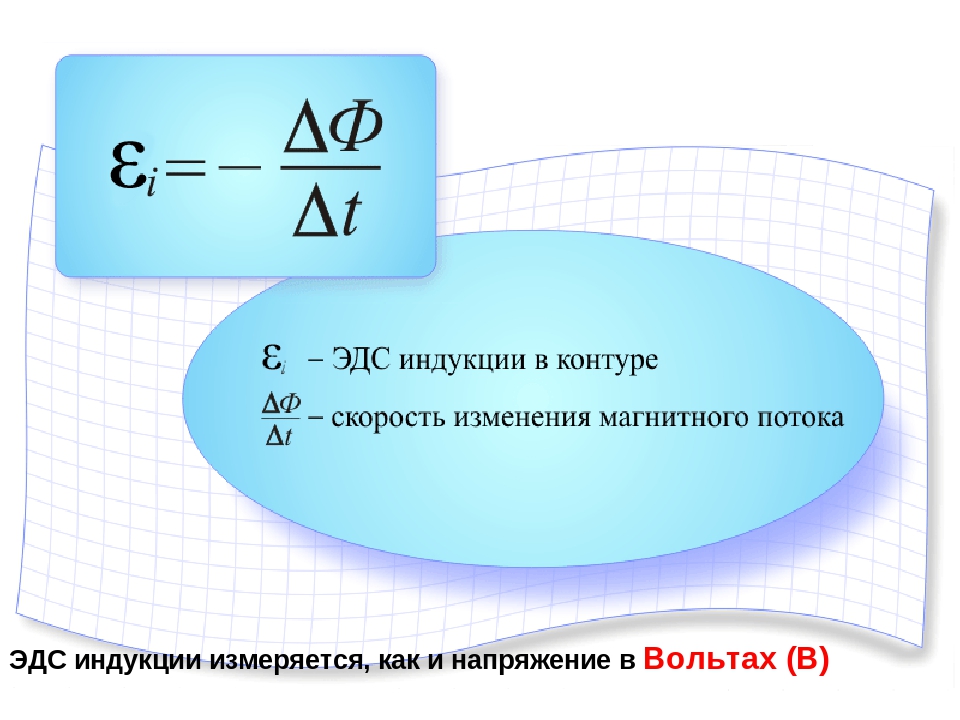 Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.

Эксперименты Фарадея

Законы Фарадея и Ленца

Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени.

Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток. Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.

Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.

Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.

Важно! Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине.

Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока.

ЭДС индукции

Формула ЭДС индукции определена как:

Е = — dФ/dt.

Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.

Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев.

Движение провода в магнитном поле

Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула:

• в случае движения проводника перпендикулярно направлению магнитного поля:

Е = — В x l x v;

• в случае движения под другим углом α:

Е = — В x l x v х sin α.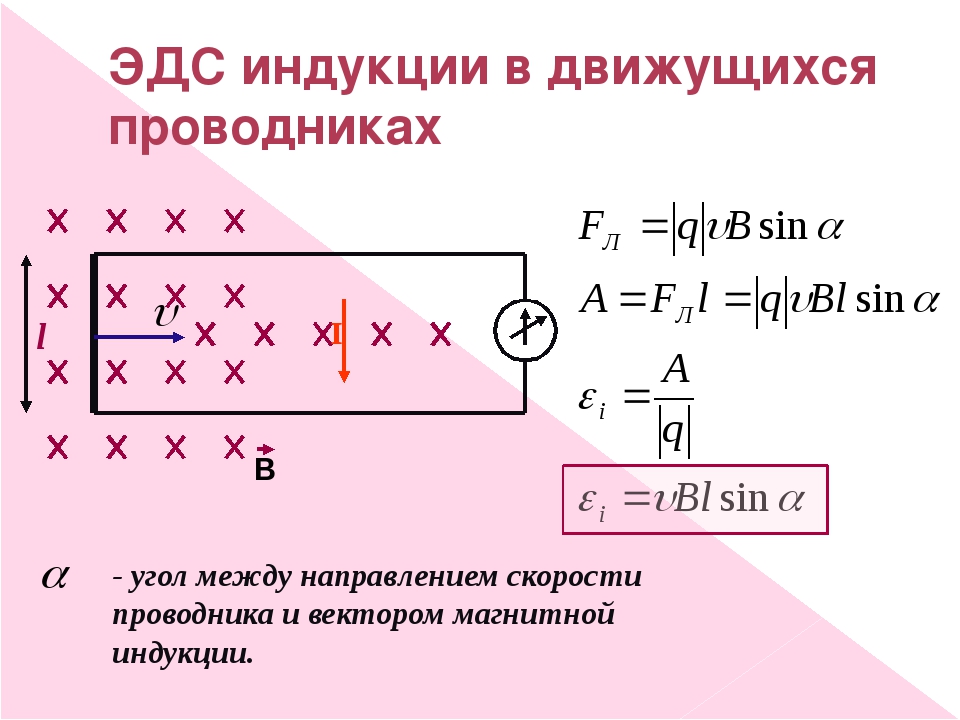

Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам.

Перемещение провода в МП

Вращающаяся катушка

Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.

ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S).

Из формулы следует, что Ф подвержен изменениям в следующих случаях:

• меняется интенсивность МП – вектор В;
• варьируется площадь, ограниченная контуром;
• изменяется ориентация между ними, заданная углом.

В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС.

Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени.

Вращение контура в МП

Важно! Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот. Графическое представление ЭДС представляет собой синусоидальную линию.

Для формулы ЭДС электромагнитной индукции применяется выражение:

Е = В х ω х S x N x sin ωt, где:

• S – площадь, ограниченная одним витком или рамкой;
• N – количество витков;
• ω – угловая скорость, с которой вращается катушка;
• В – индукция МП;
• угол α = ωt.

На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор).

ЭДС самоиндукции

Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией.

Поскольку МП пропорционально интенсивности тока, то:

Ф = L x I,

где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения.

Для ЭДС индукции формула принимает вид:

Е = — L x dI/dt.

Взаимоиндукция

Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток.

Взаимоиндукция

Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда:

1. Взаимоиндуктивность второй катушки относительно первой:

М21 = (N2 x F21)/I1;

2. Магнитный поток:

Ф21 = (М21/N2) x I1;

3. Найдем индуцированную ЭДС:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt;

4. Идентично в первой катушке индуцируется ЭДС:

Е1 = — M12 x dI2/dt;

Важно! Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой.

Взаимную индуктивность можно признать равной:

М12 = М21 = М.

Соответственно, E1 = — M x dI2/dt и E2 = M x dI1/dt.

М = К √ (L1 x L2),

где К – коэффициент связи между двумя индуктивностями.

Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.

Кроме генерирования, трансформации электроэнергии магнитная индукция применяется в иных устройствах. Например, в магнитных левитационных поездах, которые двигаются не в непосредственном контакте с рельсами, а на несколько сантиметров выше из-за электромагнитной силы отталкивания.

Видео

Оцените статью:

Глава 23. Закон электромагнитной индукции

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

(23.1)

где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м² однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

(23.2)

Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

(23.3)

где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

(23.4)

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

(23.5)

где — индуктивность контура, — сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (

задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ

1).

При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ

4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (

задача 23.2.2 — ответ 3).

Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).

Закон электромагнитной индукции. Курсы по физике

Тестирование онлайн

• Электромагнитная индукция. Основные понятия

• Закон электромагнитной индукции

ЭДС индукции в движущемся проводнике

Взаимосвязь электрических и магнитных явлений всегда интересовала физиков. Английский физик Майкл Фарадей был совершенно уверен в единстве электрических и магнитных явлений. Он рассуждал, что электрический ток способен намагнитить кусок железа. Не может ли магнит в свою очередь вызвать появление электрического тока? Эта задача была решена.

Если в постоянном магнитном поле перемещается проводник, то свободные электрические заряды внутри него тоже перемещаются (на них действует сила Лоренца). Положительные заряды концентрируются в одном конце проводника (провода), отрицательные – в другом. Возникает разность потенциалов – ЭДС электромагнитной индукции. Явление возникновения ЭДС индукции в проводнике, движущемся в постоянном магнитном поле, называется явлением электромагнитной индукции.

Правило определения направления индукционного тока (правило правой руки):

В проводнике, движущемся в магнитном поле, возникает ЭДС индукции, энергия тока в этом случае определяется по закону Джоуля-Ленца:

Работа внешней силы по перемещению проводника с током в магнитном поле

ЭДС индукции в контуре

Рассмотрим изменение магнитного потока через проводящий контур (катушку). Явление электромагнитной индукции было открыто опытным путем:

Закон электромагнитной индукции (закон Фарадея): ЭДС электромагнитной индукции, возникающая в контуре, прямо пропорциональна скорости изменения магнитного потока через него.

Знак “минус” является математическим выражением следующего правила. Направление индукционного тока, возникающего в контуре, определяется по правилу Ленца: возникающий в контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.

Закон электромагнитной индукции – формулы, определение, примеры

Магнитный поток

Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.

Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.2]

n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.

Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки

Вот, что показали эти опыты:

1. Индукционный ток возникает только при изменении линий магнитной индукции.


2. Направление тока будет различно при увеличении числа линий и при их уменьшении.


3. Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток? Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Закон Фарадея Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] N — количество витков [-]

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:

Закон Ома для проводящего контура Ɛi — ЭДС индукции [В] I — сила индукционного тока [А] R — сопротивление контура [Ом]

Если проводник длиной l будет двигаться со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B​ ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника Ɛi — ЭДС индукции [В] B — магнитная индукция [Тл] v — скорость проводника [м/с] l — длина проводника [м]

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
• вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.

Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.

Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.

Электромагнитная индукция – материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.

Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.

Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?

Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.

1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».

Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.

При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.

Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.

При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.

Вывод.

Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.

Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.

Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.

Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.

Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).

2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.

Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.

3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.

Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.

Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.

Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».

Магнитный поток

Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.

Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .

Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

Рис. 1.

В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:

(1)

Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2).

Рис. 2.

Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем . Но , поэтому

(2)

Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.

А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.

Единицей измерения магнитного потока является вебер (Вб). Как видим,

Вб = Тл · м = В · с. (3)

Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!

Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.

Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.

ЭДС индукции

Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.

Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается .

Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.

Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.

Закон электромагнитной индукции Фарадея

Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.

Если за малое время изменение магнитного потока равно , то скорость изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).

Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:

Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.

Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:

(4)

ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:

(5)

Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.

Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.

Правило Ленца

Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.

Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.

Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.

Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.

Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .

Правило Ленца позволяет находить направление индукционного тока в любой ситуации.

Рассмотрим некоторые примеры применения правила Ленца.

Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.

Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.

Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).

Рис. 3. Магнитный поток возрастает

Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает

Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.

В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.

Взаимодействие магнита с контуром

Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?

Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.

1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.

Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.

Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .

Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1

Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.

Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.

Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .

Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.

Закон Фарадея + Правило Ленца = Снятие модуля

Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.

Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.

Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .

ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.

Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.

Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: .

Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).

Рис. 5. Магнитный поток возрастает

Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.

А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, (рис. 6).

Рис. 6. Магнитный поток возрастает

Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :

(6)

Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.

Вихревое электрическое поле

Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?

Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.

Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.

Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.

Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля

Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля

Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.

Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.

1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.

Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .

Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:

Следовательно, для ЭДС индукции получаем:

ЭДС индукции в движущемся проводнике

Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.

Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле . По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9).

Рис. 9. Движение проводника в магнитном поле

Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:

Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).

Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:

(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:

(7)

Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой . Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные — к точке .

Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к — и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).

Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:

Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень проходит путь и занимает положение (рис. 9). Площадь контура возрастает на величину площади прямоугольника :

Магнитный поток через контур увеличивается. Приращение магнитного потока равно:

Скорость изменения магнитного потока положительна и равна ЭДС индукции:

Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.

На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.

Урок 5. электромагнитная индукция – Физика – 11 класс

Физика, 11 кл

Урок 5. Электромагнитная индукция

Перечень вопросов, рассматриваемых на этом уроке

1. Знакомство с явлением электромагнитной индукции.
2. Изучение законов, описывающих явление электромагнитной индукции.
3. Решение задач, практическое использование электромагнитной индукции.

Глоссарий по теме

Явление электромагнитной индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром, меняется со временем. Магнитный поток Ф – графически величина пропорциональная числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единица измерения магнитного потока: магнитный поток в один вебер создаётся однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции.

Правило Ленца: возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.

Сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

Основная и дополнительная литература по теме:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112

Рымкевич А.П. Сборник задач по физике. 10-11класс. – М.: Дрофа,2009. Стр. 28-29

ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.

Теоретический материал для самостоятельного изучения

Электрические и магнитные поля создаются одними и теми же источниками – электрическими зарядами. Отсюда естественнее было предположить, что между этими полями имеется связь. Экспериментально это предположение было доказано в 1831 г. английским учёным М. Фарадеем, открывшим явление электромагнитной индукции. Все опыты Фарадея по изучению явления электромагнитной индукции объединял один признак – магнитный поток пронизывающий замкнутый контур проводника менялся. При всяком изменении магнитного потока через замкнутый контур, в нем возникал индукционный ток.

Сила индукционного тока пропорциональна ЭДС индукции.

Направление индукционного тока менялось в зависимости от направления движения магнита относительно катушки. Это направление тока, можно найти используя правило Ленца.

М. Фарадеем экспериментально было установлено, что при изменении магнитного потока, в проводящем контуре возникает электродвижущая сила индукции, которая равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Знак минус в этой формуле отражает правило Ленца.

Закон электромагнитной индукции формулируется для ЭДС индукции.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

ЭДС индукции в движущихся проводниках:

Ɛ_i = Вlvsinα.

Джеймс Максвелл в 1860 году сделал вывод что переменное со временем магнитное поле всегда порождает вихревое электрическое поле, а переменное во времени электрическое поле в свою очередь порождает магнитное поле. Следовательно, существует единая теория электромагнитного поля.

Разбор типового контрольного задания

1.

На рисунке изображен момент демонстрационного эксперимента по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится внутри сплошного металлического кольца, но не касается его. Коромысло с металлическими кольцами может свободно вращаться вокруг вертикальной опоры. При выдвижении магнита из кольца влево кольцо будет

1) оставаться неподвижным

2) перемещаться вправо

3) совершать колебания

4) перемещаться вслед за магнитом

При выдвижении магнита из кольца влево магнитный поток от магнита через кольцо будет уменьшаться. В замкнутом кольце возникает индукционный ток. Направление этого тока по правилу Ленца такое, что создаваемое им магнитное поле препятствует изменению магнитного потока. Так как коромысло вокруг вертикальной оси может свободно вращаться, и магнитное поле магнита неоднородно, коромысло под действием сил Ампера начнёт двигаться так, чтобы препятствовать изменению магнитного потока. Следовательно, коромысло начнёт перемещаться вслед за магнитом.

Ответ:4) перемещаться вслед за магнитом.

2.

Проводник МN с длиной активной части 1м и сопротивлением 2 Ом находится в однородном магнитном поле индукцией 0,2 Тл. Проводник подключён к источнику тока с ЭДС 4 В (внутренним сопротивлением источника и сопротивлением подводящих проводников пренебречь). Какова сила тока в проводнике, если:

№1 проводник покоится;

№2 проводник движется в право со скоростью 6 м/с.

Дано:

ℓ= 1м

R = 2 Ом

В = 0,2 Тл

Ɛ = 4 В

I =?

Решение:

№1: Ток в неподвижном проводнике течёт от N к М

v = 0; Закон Ома для полной цепи I = Ɛ/R = 4В/2Ом = 2А

№2: Если проводник движется в право со скоростью 6 м/с, то по правилу правой руки индукционный ток потечёт от точки N к точке М:

Ответ: №1 2А

№2 2,6А

Наведенная ЭДС и магнитный поток

Цели обучения

К концу этого раздела вы сможете:

• Рассчитайте поток однородного магнитного поля через петлю произвольной ориентации.
• Опишите методы создания электродвижущей силы (ЭДС) с помощью магнитного поля или магнита и проволочной петли.

Аппарат, использованный Фарадеем для демонстрации того, что магнитные поля могут создавать токи, показан на рисунке 1.Когда переключатель замкнут, в катушке в верхней части железного кольца создается магнитное поле, которое передается катушке в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в катушке внизу. Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр обнаруживает ток в одном направлении в катушке внизу. (Вы также можете наблюдать это в физической лаборатории.) Каждый раз, когда переключатель открывается, гальванометр обнаруживает ток в противоположном направлении.Интересно, что если переключатель остается замкнутым или разомкнутым в течение некоторого времени, через гальванометр нет тока. Замыкание и размыкание переключателя индуцирует ток. Это изменение в магнитном поле, которое создает ток. Более важным, чем текущий ток, является ЭДС, которая его вызывает. Ток является результатом ЭДС , индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.

Рисунок 1.Аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, вызывает ЭДС и, следовательно, ток в нижней катушке. Когда переключатель разомкнут и замкнут, гальванометр регистрирует токи в противоположных направлениях. Когда переключатель остается замкнутым или разомкнутым, через гальванометр не течет ток.

Эксперимент, который легко проводится и часто проводится в физических лабораториях, показан на рисунке 2. ЭДС индуцируется в катушке, когда стержневой магнит толкается внутрь и из нее.ЭДС противоположных знаков создаются движением в противоположных направлениях, и ЭДС также меняются на противоположные за счет изменения полюсов. Те же результаты будут получены, если перемещать катушку, а не магнит – важно относительное движение. Чем быстрее движение, тем больше ЭДС, и когда магнит неподвижен относительно катушки, ЭДС отсутствует.

Рис. 2. Движение магнита относительно катушки создает ЭДС, как показано. Такие же ЭДС возникают при перемещении катушки относительно магнита.Чем больше скорость, тем больше величина ЭДС, а при отсутствии движения ЭДС равна нулю.

Метод создания ЭДС, используемый в большинстве электрических генераторов, показан на рисунке 3. Катушка вращается в магнитном поле, создавая ЭДС переменного тока, которая зависит от скорости вращения и других факторов, которые будут исследованы в следующих разделах. Обратите внимание, что генератор очень похож по конструкции на двигатель (другая симметрия).

Рис. 3. Вращение катушки в магнитном поле создает ЭДС.Это основная конструкция генератора, в котором работа по вращению катушки преобразуется в электрическую энергию. Обратите внимание, что генератор очень похож по конструкции на двигатель.

Итак, мы видим, что изменение величины или направления магнитного поля вызывает ЭДС. Эксперименты показали, что существует критическая величина, называемая магнитным потоком , Φ , определяемым

.

Φ = BA cos θ ,

, где B – напряженность магнитного поля над площадью A под углом θ к перпендикуляру к области, как показано на рисунке 5. Любое изменение магнитного потока Φ индуцирует ЭДС. Этот процесс определяется как электромагнитная индукция . Единицы магнитного потока Φ Т м ² . Как видно на рисунке 4, B cos θ = B _⊥ , который является составляющей B , перпендикулярной области A . Таким образом, магнитный поток равен Φ = B _⊥ A , произведению площади и составляющей магнитного поля, перпендикулярной ей.

Рис. 4. Магнитный поток Φ связан с магнитным полем и площадью, на которой оно существует. Поток Φ = BA cos θ связан с индукцией; любое изменение Φ вызывает ЭДС.

Вся индукция, включая приведенные до сих пор примеры, возникает из-за некоторого изменения магнитного потока Φ . Например, Фарадей изменил B и, следовательно, Φ при открытии и закрытии переключателя в своем устройстве (показано на рисунке 1).Это также верно для стержневого магнита и катушки, показанных на рисунке 2. При вращении катушки генератора угол θ и, следовательно, Φ изменяется. Насколько велика ЭДС и какое направление она принимает, зависит от изменения в Φ и от того, как быстро это изменение выполняется, как будет рассмотрено в следующем разделе.

Сводка раздела

• Ключевой величиной в индукции является магнитный поток Φ , определяемый как Φ = BA cos θ , где B – напряженность магнитного поля на площади A под углом θ к перпендикуляру к площади. .
• Единицы магнитного потока Φ Т м ² .
• Любое изменение магнитного потока Φ индуцирует ЭДС – процесс определяется как электромагнитная индукция.

Концептуальные вопросы

1. Каким образом многоконтурные катушки и железное кольцо в версии аппарата Фарадея, показанной на рисунке 1, улучшают наблюдение наведенной ЭДС?

2. Когда магнит вставляется в катушку, как показано на Рисунке 2 (а), в каком направлении катушка воздействует на магнит? Нарисуйте диаграмму, показывающую направление тока, индуцируемого в катушке, и создаваемое ею магнитное поле, чтобы обосновать вашу реакцию.Как величина силы зависит от сопротивления гальванометра?

3. Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.

4. Индуцируется ли ЭДС в катушке на рис. 5, когда она растягивается? Если да, укажите причину и укажите направление индуцированного тока.

Рис. 5. Круглая катушка с проволокой натянута в магнитном поле.

Задачи и упражнения

1. Какое значение магнитного потока в катушке 2 на рисунке 6 из-за катушки 1?

Рисунок 6.(а) Плоскости двух катушек перпендикулярны. (б) Проволока перпендикулярна плоскости катушки.

2. Какое значение магнитного потока, проходящего через катушку на Рисунке 6 (b), обусловлено проводом?

Глоссарий

магнитный поток:

величина магнитного поля, проходящего через конкретную область, рассчитанная с помощью Φ = B A cos θ , где B – напряженность магнитного поля на площади A под углом θ к перпендикуляру к площадь

электромагнитная индукция:

Процесс наведения ЭДС (напряжения) с изменением магнитного потока

Закон Фарадея

Концепция закона Фарадея состоит в том, что любое изменение магнитной среды катушки с проволокой вызывает в катушке «индуцированное» напряжение (ЭДС).Независимо от того, как производится изменение, напряжение будет генерироваться. Изменение может быть произведено изменением напряженности магнитного поля, перемещением магнита по направлению к катушке или от нее, перемещением катушки в магнитное поле или из него, вращением катушки относительно магнита и т. Д.

Слева вверху на иллюстрации две катушки пронизаны изменяющимся магнитным полем. Магнитный поток F определяется как F = BA, где B – магнитное поле или среднее магнитное поле, а A – площадь, перпендикулярная магнитному полю.Обратите внимание, что для данной скорости изменения потока через катушку генерируемое напряжение пропорционально количеству витков N, через которые проходит поток. Этот пример относится к работе трансформаторов, где магнитный поток обычно следует за железным сердечником от первичной катушки ко вторичной катушке и генерирует вторичное напряжение, пропорциональное количеству витков во вторичной катушке.

По часовой стрелке второй пример показывает напряжение, генерируемое при перемещении катушки в магнитное поле.Иногда это называют «ЭДС движения», и она пропорциональна скорости, с которой катушка перемещается в магнитное поле. Эта скорость может быть выражена через скорость изменения области, находящейся в магнитном поле.

Следующий пример – это стандартная геометрия генератора переменного тока, в которой катушка с проволокой вращается в магнитном поле. Вращение изменяет перпендикулярную площадь катушки по отношению к магнитному полю и генерирует напряжение, пропорциональное мгновенной скорости изменения магнитного потока.При постоянной скорости вращения генерируемое напряжение является синусоидальным.

Последний пример показывает, что напряжение можно генерировать, перемещая магнит к катушке с проволокой или от нее. При постоянной площади изменяющееся магнитное поле вызывает генерируемое напряжение. Направление или «смысл» генерируемого напряжения таковы, что любой результирующий ток создает магнитное поле, противодействующее изменению магнитного поля, которое его создало. Это значение знака минус в законе Фарадея, и это называется законом Ленца.

Что такое закон индукции Фарадея?

Закон индукции Фарадея описывает, как электрический ток создает магнитное поле и, наоборот, как изменяющееся магнитное поле генерирует электрический ток в проводнике. Английский физик Майкл Фарадей получил признание за открытие магнитной индукции в 1830 году; однако, по данным Техасского университета, американский физик Джозеф Генри, независимо друг от друга, сделал то же открытие примерно в то же время.

Значение открытия Фарадея невозможно переоценить.Магнитная индукция позволяет создавать электродвигатели, генераторы и трансформаторы, которые составляют основу современных технологий. Понимая и используя индукцию, мы получаем электрическую сеть и многие вещи, которые мы к ней подключаем.

Закон Фарадея был позже включен в более полные уравнения Максвелла, по словам Майкла Дубсона, профессора физики в Университете Колорадо в Боулдере. Уравнения Максвелла были разработаны шотландским физиком Джеймсом Клерком Максвеллом, чтобы объяснить взаимосвязь между электричеством и магнетизмом, по сути объединив их в единую электромагнитную силу и описав электромагнитные волны, из которых состоят радиоволны, видимый свет и рентгеновские лучи.

Электричество

Электрический заряд – фундаментальное свойство материи, согласно Рочестерскому технологическому институту. Хотя трудно описать, что это на самом деле, мы хорошо знакомы с тем, как он ведет себя и взаимодействует с другими зарядами и полями. По словам Серифа Урана, профессора физики в Питтсбургском государственном университете, электрическое поле от локализованного точечного заряда относительно просто. Он описывает его как излучающий одинаково во всех направлениях, как свет от голой лампочки, и уменьшающийся в силе как обратный квадрат расстояния (1/ r ² ) в соответствии с законом Кулона.Когда вы отодвигаетесь вдвое дальше, напряженность поля уменьшается до одной четвертой, а когда вы удаляетесь в три раза дальше, она уменьшается до одной девятой.

Протоны имеют положительный заряд, а электроны – отрицательный. Однако протоны в основном иммобилизованы внутри атомных ядер, поэтому перенос заряда из одного места в другое выполняют электроны. Электроны в проводящем материале, таком как металл, в значительной степени могут свободно перемещаться от одного атома к другому по своим зонам проводимости, которые являются высшими электронными орбитами.Достаточная электродвижущая сила (ЭДС) или напряжение вызывает дисбаланс заряда, который может заставить электроны перемещаться по проводнику из области с более отрицательным зарядом в область с более положительным зарядом. Это движение мы называем электрическим током.

Магнетизм

Чтобы понять закон индукции Фарадея, важно иметь базовые представления о магнитных полях. По сравнению с электрическим полем магнитное поле более сложное. По данным Государственного университета Сан-Хосе, хотя положительные и отрицательные электрические заряды могут существовать отдельно, магнитные полюса всегда приходят парами – северный и южный.Как правило, магниты всех размеров – от субатомных частиц до магнитов промышленных размеров до планет и звезд – являются диполями, то есть каждый из них имеет два полюса. Мы называем эти полюса северным и южным по направлению, в котором указывают стрелки компаса. Интересно, что поскольку противоположные полюса притягиваются и, как полюса, отталкиваются, северный магнитный полюс Земли на самом деле является южным магнитным полюсом, потому что он притягивает северные полюса стрелок компаса.

Магнитное поле часто изображают в виде линий магнитного потока.В случае стержневого магнита силовые линии выходят из северного полюса и изгибаются, чтобы снова войти в южный полюс. В этой модели количество силовых линий, проходящих через заданную поверхность в пространстве, представляет собой плотность потока или напряженность поля. Однако следует отметить, что это всего лишь модель. Магнитное поле гладкое и непрерывное и на самом деле не состоит из дискретных линий.

Силовые линии магнитного поля от стержневого магнита. (Изображение предоставлено snapgalleria Shutterstock)

Магнитное поле Земли создает огромный магнитный поток, но он рассеивается по огромному пространству.Следовательно, только небольшое количество потока проходит через данную область, что приводит к относительно слабому полю. Для сравнения, магнитный поток от магнита-холодильника крошечный по сравнению с магнитным потоком Земли, но его напряженность поля во много раз сильнее на близком расстоянии, где его силовые линии гораздо более плотно упакованы. Однако по мере удаления поле быстро становится намного слабее.

Индукция

Если пропустить через провод электрический ток, вокруг него возникнет магнитное поле.Направление этого магнитного поля можно определить по правилу правой руки. По данным физического факультета Университета штата Нью-Йорк Буффало, если вы вытянете большой палец и согнете пальцы правой руки, ваш большой палец будет указывать в положительном направлении тока, а пальцы согнуты в северном направлении магнитного поля. .

Правило левой и правой руки для магнитного поля, вызванного током в прямом проводе. (Изображение предоставлено Фуадом А. Саадом Shutterstock)

Если вы согнете провод в петлю, силовые линии магнитного поля согнутся вместе с ним, образуя тороид или форму пончика.В этом случае ваш большой палец указывает в северном направлении магнитного поля, выходящего из центра петли, а ваши пальцы будут указывать в положительном направлении тока в петле.

В круговой петле с током (а) правило правой руки определяет направление магнитного поля внутри и снаружи петли. (б) Более подробное отображение поля, подобное полю стержневого магнита. (Изображение предоставлено OpenStax)

Если мы пропустим ток через проволочную петлю в магнитном поле, взаимодействие этих магнитных полей вызовет скручивающую силу или крутящий момент в петле, заставляя ее вращаться, согласно данным Рочестерского института. Технология.Однако он будет вращаться только до тех пор, пока магнитные поля не выровняются. Если мы хотим, чтобы петля продолжала вращаться, мы должны изменить направление тока, что изменит направление магнитного поля петли. Затем петля повернется на 180 градусов, пока ее поле не выровняется в другом направлении. Это основа электродвигателя.

И наоборот, если мы вращаем проволочную петлю в магнитном поле, поле будет индуцировать электрический ток в проводе. Направление тока меняется каждые пол-оборота, создавая переменный ток.Это основа электрогенератора. Здесь следует отметить, что это не движение провода, а скорее размыкание и замыкание петли по отношению к направлению поля, которое индуцирует ток. Когда петля обращена лицом к полю, через петлю проходит максимальное количество магнитного потока. Однако, когда петля повернута ребром к полю, силовые линии не проходят через петлю. Именно это изменение величины магнитного потока, проходящего через контур, вызывает ток.

Другой эксперимент, который мы можем провести, – сформировать из провода петлю и подключить концы к чувствительному измерителю тока или гальванометру.Если затем протолкнуть стержневой магнит через петлю, стрелка гальванометра переместится, указывая на индуцированный ток. Однако, как только мы останавливаем движение магнита, ток возвращается к нулю. Поле от магнита будет индуцировать ток только тогда, когда он увеличивается или уменьшается. Если мы вытащим магнит обратно, он снова вызовет ток в проводе, но на этот раз он будет в противоположном направлении.

Магнит в проволочной петле, подключенной к гальванометру. (Изображение предоставлено: Фуад А.Saad Shutterstock)

Если бы мы включили в цепь лампочку, она рассеивала бы электрическую энергию в виде света и тепла, и мы бы чувствовали сопротивление движению магнита, когда мы перемещали его внутрь и из контура. . Чтобы переместить магнит, мы должны совершить работу, эквивалентную энергии, используемой лампочкой.

В еще одном эксперименте мы могли бы построить две проволочные петли, подключить концы одной к батарее с помощью переключателя, а концы другой петли подключить к гальванометру.Если мы поместим две петли близко друг к другу лицом к лицу и включим питание первой петли, гальванометр, подключенный ко второй петле, покажет индуцированный ток, а затем быстро вернется к нулю.

Здесь происходит то, что ток в первом контуре создает магнитное поле, которое, в свою очередь, индуцирует ток во втором контуре, но только на мгновение, когда магнитное поле изменяется. Когда вы выключаете переключатель, счетчик на мгновение отклоняется в противоположном направлении.Это еще один признак того, что ток индуцирует изменение интенсивности магнитного поля, а не его сила или движение.

Объяснение этому состоит в том, что магнитное поле заставляет электроны в проводнике двигаться. Это движение называется электрическим током. В конце концов, однако, электроны достигают точки, в которой они находятся в равновесии с полем, и в этой точке они перестают двигаться. Затем, когда поле снимается или выключается, электроны возвращаются в свое исходное положение, создавая ток в противоположном направлении.

В отличие от гравитационного или электрического поля, магнитное дипольное поле представляет собой более сложную трехмерную структуру, сила и направление которой различаются в зависимости от места измерения, поэтому для ее полного описания требуется расчет. Однако мы можем описать упрощенный случай однородного магнитного поля – например, очень маленький участок очень большого поля – как Φ B = BA , где Φ B – абсолютное значение магнитного потока. , B, – это напряженность поля, а A – это определенная область, через которую проходит поле.И наоборот, в этом случае напряженность магнитного поля – это поток на единицу площади, или B = Φ B / A .

Закон Фарадея

Теперь, когда у нас есть базовое представление о магнитном поле, мы готовы определить закон индукции Фарадея. Он утверждает, что индуцированное напряжение в цепи пропорционально скорости изменения во времени магнитного потока, проходящего через эту цепь. Другими словами, чем быстрее изменяется магнитное поле, тем больше будет напряжение в цепи.Направление изменения магнитного поля определяет направление тока.

Увеличить напряжение можно за счет увеличения количества витков в цепи. Индуцированное напряжение в катушке с двумя петлями будет вдвое больше, чем с одной петлей, а с тремя петлями – втрое. Вот почему настоящие двигатели и генераторы обычно имеют большое количество катушек.

Теоретически моторы и генераторы одинаковы. Если вы включите двигатель, он будет вырабатывать электричество, а подача напряжения на генератор заставит его вращаться.Однако большинство реальных двигателей и генераторов оптимизированы только для одной функции.

Трансформаторы

Еще одним важным приложением закона индукции Фарадея является трансформатор, изобретенный Никой Тесла. В этом устройстве переменный ток, который меняет направление много раз в секунду, проходит через катушку, намотанную вокруг магнитного сердечника. Это создает изменяющееся магнитное поле в сердечнике, которое, в свою очередь, индуцирует ток во второй катушке, намотанной вокруг другой части того же магнитного сердечника.

Схема трансформатора (Изображение предоставлено photoiconix Shutterstock)

Отношение числа витков в катушках определяет соотношение напряжения между входным и выходным током. Например, если мы возьмем трансформатор со 100 витками на входе и 50 витками на выходе, и введем переменный ток 220 вольт, выход будет 110 вольт. Согласно Hyperphysics, трансформатор не может увеличивать мощность, которая является произведением напряжения и тока, поэтому, если напряжение повышается, ток пропорционально понижается, и наоборот.В нашем примере входное напряжение 220 В при 10 А или 2200 Вт даст на выходе 110 В при 20 А, опять же 2200 Вт. На практике трансформаторы никогда не бывают идеально эффективными, но, по данным Техасского университета, потери мощности хорошо спроектированного трансформатора обычно составляют всего несколько процентов.

Трансформаторы делают возможной электрическую сеть, от которой мы зависим для нашего промышленного и технологического общества. Линии электропередачи по пересеченной местности работают под напряжением в сотни тысяч вольт, чтобы передавать больше энергии в пределах допустимого для проводов тока.Это напряжение многократно понижается с помощью трансформаторов на распределительных подстанциях, пока оно не достигнет вашего дома, где оно, наконец, понижается до 220 и 110 вольт, которые могут запустить вашу электрическую плиту и компьютер.

Дополнительные ресурсы

Закон Фарадея

Закон Фарадея
Следующая: Закон Ленца Up: Магнитная индукция Предыдущий: Магнитная индукция Явление магнитной индукции играет решающую роль в три очень полезных электрических устройства: электрогенератор , , электрогенератор . двигатель и трансформатор .Без этих устройств современная жизнь была бы невозможно в нынешнем виде. Магнитная индукция была открыта в 1830 г. Английский физик Майкл Фарадей. Американский физик Джозеф Генри независимо друг от друга сделал то же открытие примерно в одно и то же время. Оба физиков заинтриговал тот факт, что электрический ток, протекающий вокруг цепь может генерировать магнитное поле. Наверняка, рассуждали они, если электрический ток может генерировать магнитное поле, тогда магнитное поле должно каким-то образом быть способным генерировать электрический ток.Однако потребовалось много лет бесплодных экспериментов. прежде, чем они смогли найти необходимый ингредиент, который позволяет магнитное поле для генерации электрического тока. Этот ингредиент – изменение времени .

Рассмотрим плоскую петлю из токопроводящего провода соответствующей площади поперечного сечения. Поместим эту петлю в магнитное поле, напряженность которого приблизительно равна равномерный по всей длине петли. Предположим, что направление магнитное поле образует угол с нормальным направлением к петля.Магнитный поток через петлю равен определяется как произведение площади петли и составляющей магнитное поле, перпендикулярное петле. Таким образом,

(191)

Если цикл оборачивается вокруг себя раз (, т.е. , если цикл имеет витков ) то магнитный поток через петлю просто умножить на магнитный поток на один виток:

(192)

Наконец, если магнитное поле неоднородно по петле или петля не лежать в одной плоскости, тогда мы должны оценить магнитный поток как поверхностный интеграл

(193)

Вот какая-то поверхность, к которой прикреплена.Если петля имеет витки, то поток в несколько раз превышает указанное выше значение. Единица измерения магнитного потока в системе СИ – вебер (Вб). Одна тесла эквивалентна один вебер на квадратный метр:

(194)

Фарадей обнаружил, что если магнитное поле проходит через петлю из проволоки изменяется во времени , тогда вокруг контура наводится ЭДС. Фарадей смог наблюдать этот эффект, потому что ЭДС вызывает ток, циркулирующий в петле.Фарадей обнаружил, что величина ЭДС прямо пропорциональна скорости изменения магнитного поля во времени. Он также обнаружил, что ЭДС генерируется, когда петля провода перемещается на из области низкой напряженности магнитного поля в область высокой напряженности магнитного поля, и наоборот . ЭДС прямо пропорциональна скорость, с которой петля перемещается между двумя областями. Ну наконец то, Фарадей обнаружил, что ЭДС генерируется вокруг петли, которая на вращается на в однородном магнитном поле постоянной напряженности.В этом случае ЭДС прямо пропорциональна скорости вращения петли. Фарадей в конце концов в состоянии предложить единый закон, который мог объяснить все его многочисленные и разнообразные наблюдения. Этот закон, известный как Закон магнитной индукции Фарадея выглядит следующим образом:

ЭДС, наведенная в цепи, пропорциональна скорости изменения во времени магнитный поток, связывающий эту цепь.

Единицы СИ были зафиксированы таким образом, чтобы константа пропорциональности в этом закон единицы .Таким образом, если магнитный поток через цепь изменяется на сумму во временном интервале тогда генерируемая в цепи ЭДС равна

(195)

Есть много разных способов, которыми магнитный поток связывает электрическая цепь может менять. Может измениться либо напряженность магнитного поля, либо направление магнитного поля. поле может измениться, или положение цепи может измениться, или форма цепь может измениться, или ориентация цепи может измениться.Закон Фарадея гласит, что все эти способы полностью эквивалент в части генерации ЭДС вокруг цепь касается.

---

Следующая: Закон Ленца Up: Магнитная индукция Предыдущий: Магнитная индукция

Ричард Фицпатрик 2007-07-14

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

---

Рис 32.1 показан стержень из проводящего материала, перемещаемый с помощью скорость v в однородном магнитном поле B. Магнитная сила, действующая на свободную электрон в стержне будет направлен вверх и имеет величину

(32.1)

Рисунок 32.1. Движущийся проводник в магнитном поле. В результате действия магнитной силы электроны начнут накапливаются в верхней части стержня. Распределение заряда стержня будет поэтому измените, и верхушка стержня будет иметь избыток электронов (отрицательный заряд), а нижняя часть стержня будет иметь дефицит электронов (положительный заряд).Это распределение заряда будет создавать электрическое поле в стержень. Напряженность этого электрического поля будет увеличиваться до тех пор, пока электростатическая сила, создаваемая этим полем, равна по величине магнитная сила. В этот момент восходящий поток электронов остановится и

(32,2)

или

(32,3)

Индуцированное электрическое поле будет создавать разность потенциалов [Delta] V между концами стержня, равный

(32.4)

где L – длина стержня. Если концы стержня соединены с цепи, обеспечивающей возврат накопленного заряда, стержень будет источник ЭДС. Поскольку ЭДС связана с движением стержня через магнитное поле называется ЭДС движения . Уравнение (32.4) показывает, что величина ЭДС пропорциональна скорости v. на рисунке 32.1 мы видим, что vL – это площадь, пройденная стержнем на второй.Величина BvL – это магнитный поток, проходящий через стержень на второй. Таким образом

(32,5)

Хотя эта формула была получена для особого случая, показанного на рис. 32.1, она действительно в целом. Предназначен для перемещения стержней и проволоки произвольной формы. через произвольные магнитные поля.

Уравнение (32.5) связывает наведенную ЭДС со скоростью, с которой магнитный поток изменяется. В системе, показанной на рисунке 32.1 вложенный флюс изменяется из-за движения стержня. Вложенный магнитный поток также может быть изменяется при изменении напряженности приложенного магнитного поля. В обоих случаях результатом будет наведенная ЭДС. Связь между наведенной ЭДС и изменение магнитного потока известно как закон индукции Фарадея:

“Индуцированная ЭДС при движении или изменении математической траектории при постоянной или изменение магнитного поля равно скорости, с которой магнитный поток проходит через тропинка.”

Если рассматривать замкнутый путь, закон Фарадея можно сформулировать так:

«Индуцированная ЭДС вокруг замкнутого математического пути в магнитном поле равна к скорости изменения магнитного потока, перехваченного областью в пределах путь “

или

(32,6)

Знак минус в уравнении (32.6) показывает, насколько полярность наведенной ЭДС связаны со знаком потока и скоростью изменения потока.Знак поток фиксируется правилом правой руки:

“Согните пальцы правой руки в том направлении, в котором мы расчет ЭДС вокруг пути; тогда магнитный поток будет положительным, если линии магнитного поля указывают в направлении большого пальца, а отрицательные иначе. “

Пример: Задача 32.13

Металлический стержень длиной L и массой m скользит свободно, без трения, на двух параллельных металлических рельсах.Дорожки соединяются одним концом так, чтобы они и стержень образуют замкнутый контур (см. рисунок 32.2). У стержня есть сопротивление R, и гусеницы имеют незначительное сопротивление. Однородное магнитное поле перпендикулярно плоскости этого контура. Магнитное поле увеличивается при постоянной скорости дБ / дт. Первоначально магнитное поле имеет силу B ₀ и стержень покоится на расстоянии x ₀ от соединенный конец рельсов. Выразите ускорение стержня при этом момент в заданных количествах.

Рисунок 32.2. Проблема 32.13.

Магнитный поток [Phi], заключенный между стержнем и дорожками в момент времени t = 0 с, равен выдано

(32,7)

Магнитное поле увеличивается с постоянной скоростью, и, следовательно, закрытый магнитный поток также увеличивается:

(32,8)

Теперь для определения наведенной ЭДС можно использовать закон индукции Фарадея:

(32.9)

В результате наведенной ЭДС через стержень будет протекать ток с величина равна

(32.10)

Направление тока вдоль провода и, следовательно, перпендикулярно к магнитное поле. Сила, действующая на стержень со стороны магнитного поля, равна выдано

(32,11)

(см. главу 31). Комбинируя уравнения (32.10) и (32.11), получаем для силы на провод

(32.12)

Таким образом, ускорение стержня в момент времени t = 0 с равно

. (32,13) ​​

Пример: Задача 32.12

a) Длинный соленоид имеет 300 витков провода на метр и радиус 3,0 см. Если ток в проводе увеличивается со скоростью 50 А / с, то Скорость увеличения напряженности магнитного поля в соленоиде?

б) Соленоид окружен катушкой на 120 витков.Радиус этого катушка 6.0 см. Какая наведенная ЭДС будет генерироваться в этой катушке, пока ток в соленоиде увеличивается?

а) Магнитное поле в соленоиде обсуждалось в главе 31. Если соленоид имеет n витков на метр, и если I – ток через каждую катушку, то поле внутри соленоида равно

(32,14)

Следовательно,

(32,15)

В этой задаче n = 300 витков / метр и dI / dt = 50 A / s.Изменение в магнитное поле, таким образом, равно

(32,16)

Это уравнение показывает, что магнитное поле увеличивается со скоростью 0,019 Т / с.

б) Поскольку магнитное поле в соленоиде меняется, магнитный поток окруженная окружающей катушкой также изменится. Поток, заключенный в одинарная обмотка этой катушки

(32,17)

где r _в = 3.0 см – радиус соленоида. Здесь у нас есть Предполагалось, что напряженность магнитного поля вне соленоида равна нулю. Суммарный поток, охватываемый внешними катушками, равен

. (32,18)

Скорость изменения магнитного потока из-за этого изменения магнитного поля равна выдано

(32,19)

В результате изменения тока в соленоиде будет наведена ЭДС во внешней катушке, со значением, равным

(32.20)

Если концы катушки соединены, ток будет течь через дирижер. Направление тока в катушке можно определить с помощью Закон Ленца , который гласит, что

«Индуцированные ЭДС всегда имеют такую ​​полярность, чтобы противодействовать изменение, которое их порождает “

Применим закон Ленца к задаче 32.12. Направление магнитного поля может быть определен с помощью правила правой руки и указывается вправо.Если ток в соленоиде увеличивается, магнитный поток также увеличивается. Электрический ток во внешней катушке будет течь в таком направлении, чтобы противодействовать этому изменению. Это означает, что ток в этой катушке будет течь против часовой стрелки ( поле, создаваемое индуцированным током, направлено противоположно полю генерируется большим соленоидом).

Стержень, движущийся в магнитном поле, будет иметь наведенную ЭДС в результате магнитная сила, действующая на свободные электроны.Индуцированная ЭДС будет пропорциональна линейной скорости v стержня. Если мы посмотрим на стержень из в системе отсчета, в которой стержень покоится, магнитная сила будет равна нулю. Однако все же должна быть наведенная ЭДС. Поскольку эта ЭДС не может быть генерируется магнитным полем, оно должно быть вызвано электрическим полем, которое существует в движущейся системе отсчета. Величина этого электрического поля должен быть таким, чтобы создавалась такая же наведенная ЭДС, что и в система отсчета, в которой движется стержень.Для этого требуется

(32.21)

Электрическое поле E ‘, существующее в системе отсчета движущегося стержня, равно называется индуцированное электрическое поле . ЭДС, возникающая между концы стержня

(32.22)

что эквивалентно уравнению (32.4). Если индуцированное электрическое поле имеет положение зависимой, то мы должны заменить уравнение (32.22) интегральным выражением

(32.23)

где интеграл простирается от одного конца стержня до другого конца стержня. стержень.

Разница между наведенным электрическим полем и электрическим полем порожденная распределением статического заряда, состоит в том, что в первом случае поле не является консервативным и интеграл по путям по замкнутому пути равен

(32,24)

который не равен нулю, если магнитный поток зависит от времени.

Изменение тока в проводнике (например, в катушке) приводит к изменению магнитного поля. поле.Это зависящее от времени магнитное поле может индуцировать ток за секунду. проводник, если он помещен в это поле. ЭДС, наведенная в эту секунду проводник, [эпсилон] ₂ , будет зависеть от магнитного потока через этот проводник:

(32,25)

Поток [Phi] _B1 зависит от напряженности магнитного поля. генерируется проводником 1 и, следовательно, пропорционален току Я ₁ через этот проводник:

(32.26)

Здесь постоянная L ₂₁ зависит от размера двух катушек, от расстояние между ними и количество витков в каждой катушке. В Константа L ₂₁ называется взаимной индуктивностью двух катушек. Используя эту константу, уравнение (32.25) можно переписать как

(32,27)

Единицей индуктивности является Генри (Гн), и из уравнения (32.27) мы заключаем, что

(32,28)

Когда магнитное поле, создаваемое катушкой, изменяется (из-за изменения ток) магнитный поток, заключенный в катушке, также изменится.Это изменение в потоке вызовет ЭДС в катушке, и поскольку ЭДС возникает из-за изменения ток через катушку называется ЭДС самоиндукции. В самоиндуцированная ЭДС равна

(32.29)

В уравнении (32.29) L называется собственной индуктивностью катушки. Самоиндуцированная ЭДС будет действовать в таком направлении, чтобы противодействовать изменению Текущий.

Пример: Задача 32.32

Длинный соленоид радиуса R имеет n витков на единицу длины.Циркуляр катушка из проволоки радиуса R ‘с n’ витками окружает соленоид. Что это взаимная индукция? Имеет ли значение форма катушки с проволокой?

Предполагается, что поле внутри соленоида бесконечно длинное. соленоид и имеет силу равную

(32.30)

Поток, заключенный во внешнюю катушку, равен

(32.31)

Индуцированная ЭДС во внешней катушке равна

(32.32)

Таким образом, взаимная индуктивность L ₁₂ равна

. (32,33)

Если через индуктор протекает постоянный ток, не зависящий от времени магнитный поле создано. Если внезапно отключится источник тока, изменение в заключенном магнитном потоке будет генерировать самоиндуцированную ЭДС, которая будет пытаться чтобы ток продолжал течь в первоначальном направлении. Электроэнергия доставляемая самоиндуцированной ЭДС изначально накапливалась в катушке индуктивности в форма магнитной энергии.Количество магнитной энергии, хранящейся в магнитном поле может быть определено путем расчета общей мощности, передаваемой мощностью источник для создания магнитного поля. Предположим, что после того, как батарея подключенный к катушке индуктивности, ток увеличивается со скоростью dI / dt. В самоиндуцированная ЭДС, создаваемая этим зависящим от времени током, равна

(32,34)

Ток должен обеспечивать дополнительную мощность, чтобы преодолеть эту самоиндуцированную ЭДС. В требуемая мощность будет зависеть от времени и равна

(32.35)

Работа, совершаемая током, сохраняется в индукторе в виде магнитной энергии. В изменение dU в магнитной энергии индуктора, таким образом, равно

(32,36)

Полная энергия, запасенная в магнитном поле индуктора, когда ток достигает своего окончательного значения, может быть получено интегрированием уравнения (32.36) между I = 0 и I = I _f .

(32,37)

Для соленоида длиной l собственная индуктивность равна

. (32.38)

Таким образом, магнитная энергия, запасенная в соленоиде, равна

. (32,39)

где V – объем соленоида. Магнитная энергия может быть выражена в условия Б и В:

(32,40)

где B = u ₀ n I – магнитное поле в соленоиде. Общая магнитная энергия индуктора теперь может быть выражена через Плотность магнитной энергии u, которая определяется как

(32.41)

Магнитная энергия, запасенная в магнитном поле, равна плотности энергии время объем. Хотя мы вывели формулу для магнитной энергии плотности для частного случая очень длинного соленоида, его вывод действителен для любого произвольного магнитного поля.

Пример: Задача 32.46

Тороид квадратного сечения имеет внутренний радиус R ₁ и внешний радиус R ₂ .Тороид имеет N витков провода, несущего ток I; Предположим, что N очень велико.

а) Найдите плотность магнитной энергии как функцию радиуса.

б) Интегрируя плотность энергии, найдите полную магнитную энергию, хранящуюся в соленоид.

c) Выведите самоиндуктивность по формуле U = L ^. I ² /2.

а) Примените закон Ампера, используя сферическую петлю Ампера с радиусом r

(32.42)

Ток, заключенный в амперовскую петлю, равен

. (32,43)

Используя закон Ампера, мы можем определить магнитное поле B:

(32,44)

Таким образом, плотность магнитной энергии равна

(32,45)

б) Пусть высота тороида равна h. Рассмотрим кусочек тороид показан на рисунке 32.3.

Рисунок 32.3. Сечение тороида задачи 32.46. Объем dV этого среза равен

(32,46)

Магнитная энергия, запасенная в этом сегменте, равна

(32,47)

Полная магнитная энергия, запасенная в тороиде, может быть получена путем интегрирования уравнение (32,47) относительно r между r = ₁ и r = ₂ :

(32,48)

в) Магнитная энергия, запасенная в индукторе с индуктивностью L, равна 0.5 л Я ² . Сравнивая это с уравнением (32.48), мы заключаем, что собственная индуктивность L тороида равна

(32,49)

Цепь RL состоит из резистора и катушки индуктивности, включенных последовательно с аккумулятор (см. рисунок 32.4). Применяя к этому второму правилу Кричгофа по одноконтурной схеме получаем следующее дифференциальное уравнение

(32.50)

Рисунок 32.4. Схема RL. Это дифференциальное уравнение имеет решение

(32,51)

Это решение действительно, если батарея подключена при t = 0. Уравнение (32.51) показывает, что ток при t = 0 с равен 0 и неуклонно растет, достигая окончательное значение e / R при t = [бесконечность]. Постоянная времени цепи RL равна L / R. Если ток достиг постоянного значения и батарея внезапно разряжена. отключен, проводник может генерировать ток через резистор, который будет постепенно распадаться со временем.Если начальный ток равен [epsilon] / R, ток в момент времени t будет равен

(32,52)

Пример: Задача 32.54

Сколько джоулева тепла рассеивается током в уравнении (32,52) в резистор в интервале времени между t = 0 и t = [бесконечность]? Сравнить с начальная магнитная энергия в индукторе.

Ток через резистор указан в уравнении (32.51). Рассеиваемая мощность по этому ток в резисторе равен

(32.53)

Полная энергия, рассеиваемая этим током в резисторе между t = 0 и t = [бесконечность] равно

(32,54)

Магнитная энергия, запасенная в индукторе, равна

(32,55)

и мы заключаем, что вся магнитная энергия, запасенная в индукторе, рассеивается как джоулево тепло в резисторе.

---

Комментарии, вопросы и / или предложения отправляйте по электронной почте на адрес wolfs @ nsrl.rochester.edu и / или посетите домашнюю страницу Фрэнка Вольфса.

Наведенные токи и поля

Энергия кванта электромагнитных полей частотой 50 Гц слишком мала для разрыва химических связей. Ясно, что ЭМП промышленной частоты или излучение не вызывают ионизацию так же, как рентгеновские лучи или альфа-частицы. Вместо этого, основной известный способ взаимодействия полей 50 Гц с людьми – это индукция токов.

Микрошоки – это связанное, но другое явление.

Какие токи производят магнитные поля?

Любое переменное магнитное поле будет индуцировать электрическое поле, которое, в свою очередь, создает ток в проводящей среде.Человеческое тело является проводящим, и поэтому в нем будет индуцированный ток, хотя, как правило, очень слабый. Как показано справа, ток циркулирует по телу.

При расчетах промышленной частоты принято считать, что человеческое тело имеет радиус 0,2 м и проводимость 0,2 См · м ^-1 . Используя эту модель, магнитное поле в 160 микротесла (мкТл) индуцирует периферийную плотность тока 1 мА · м ^-2 . Могут быть выполнены более точные численные расчеты, учитывающие фактическую форму тела и различную проводимость различных тканей.

Какие токи производят электрические поля?

Переменные электрические поля также вызывают токи в теле. Как показано справа, для вертикального поля они бегают вверх и вниз по телу. При расчете необходимо учитывать возмущение поля, вызванное самим телом. Для обычного человека, стоящего в вертикальном поле, ток 1 мА через тело индуцируется силой 70 кВ · м ^-1 ; подробнее о численных расчетах.

Действие наведенных токов на тело

Внутри тела токи, индуцированные полями, имеют тот же диапазон эффектов, что и токи, вводимые через электроды, например.грамм. при поражении электрическим током. Но эти эффекты полностью зависят от силы тока. Таким образом, плотность тока около 0,1 А · м ^-2 может стимулировать возбудимую ткань, а плотность тока выше приблизительно 1 А · м ^-2 может вызывать фибрилляцию желудочков, а также вызывать нагрев. Однако эти плотности тока соответствуют полям, намного большим, чем когда-либо встречались при 50 Гц.

Сообщается о ряде возможных эффектов при более низких полях. Установленный эффект, наблюдаемый у людей при самом низком магнитном поле, – это эффект магнитофосфена, когда в периферическом зрении возникает ощущение мерцания магнитными полями с частотой 50 Гц и выше примерно 10 мТл (т.е.е. 10000 мкТл). Магнитофосфены, вероятно, вызваны индуцированной плотностью тока в сетчатке; порог на 20 Гц (наиболее чувствительная частота) составляет около 20 мА · м ^-2 .

Микроудары – это связанное, но отдельное явление, вызванное не постоянным током, а одноразовым разрядом.

Какой безопасный уровень наведенного тока?

Нормы воздействия обычно предназначены для предотвращения всех эффектов наведенных токов на том основании, что любое воздействие на мозг или нервную систему потенциально вредно.Например, руководство ICNIRP в настоящее время рекомендует, чтобы люди на работе не подвергались воздействию плотностей тока в голове, шее и туловище более 10 мА · м ^-2 («основное ограничение») с нижним пределом 2 мА · м ^-2 для населения в целом, которое может включать людей, более чувствительных по медицинским показаниям.

Узнайте больше о том, как рассчитываются наведенные токи

электрических цепей – Индуцированная ЭДС и ЭДС батареи

Меня немного смущает, одинаковы ли наведенная ЭДС и ЭДС батареи по своей природе, различаясь только их источником.

Нет, они очень разные. ЭДС батареи возникает из-за химических реакций внутри батареи и действует только на частицы внутри батареи, поэтому она направляет ток только по пути внутри батареи; вне батареи ток управляется другими видами сил, такими как электростатическое или индуцированное электрическое поле.

Индуцированная ЭДС возникает из-за индуцированного электрического поля, которое присутствует везде, где магнитное поле изменяется во времени, оно управляет током во всех частях цепи, хотя насколько сильно зависит от силы индуцированного электрического поля в этом месте.

Существует ли градиент потенциала в случае наведенной ЭДС, как при подключении батареи к цепи?

На практике это часто случается, но не напрямую из-за индуцированного поля. Видите ли, индуцированное поле – это соленоидальное поле (движется по кругу, не имеет источника или стока), и такое поле не может быть описано потенциальной функцией. Однако индуцированное поле действует на подвижные заряды в проводниках и способно концентрировать или истощать их в различных областях пространства, например на поверхности и выводах индуктора.Эти поверхностные заряды создают кулоновское электрическое поле, которое действительно имеет потенциал. Когда мы говорим, что существует разность потенциалов на элементе схемы, таком как резистор, конденсатор или индуктор, мы имеем в виду потенциал кулоновского поля поверхностных зарядов в системе. Это не имеет ничего общего с индуцированным полем.

В идеальном индукторе действие кулоновского поля нейтрализует влияние индуцированного поля. Поэтому когда ЭДС для катушки индуктивности (сеть индуцированного поля на единицу заряда) обычно записывается со знаком минус как $$ EMF = -L \ frac {dI} {dt} ~~~~ \ tag {*} $$ чтобы соответствовать закону Ленца, падение потенциала в том же положительном направлении (часто называемое напряжением на элементе), которое мы используем при записи закона напряжения Кирхгофа, равно $$ п.d. = L \ frac {dI} {dt} $$ т.е. имеет противоположный знак. Для индуктора с заметным омическим сопротивлением $ R $ кулоновское поле не компенсирует индуцированное поле полностью и падение потенциала составляет $$ p.d. = L \ frac {dI} {dt} + RI $$ в то время как индуцированная ЭДС по-прежнему дается (*).

Теоретически индуцированное поле может присутствовать без градиента электрического потенциала, если установка достаточно симметрична. Например, если индуцированное поле возникает из-за движущегося цилиндрического магнита, имеющего пренебрежимо малую плотность электрического заряда, его кулоновское поле незначительно, а потенциал не изменяется под действием индуцированного поля.Мы даже можем добавить токопроводящую круговую дорожку; если мы разместим его так, чтобы круговое индуцированное поле действовало одинаково на подвижные заряды во всех частях круглого проводника, то в проводнике не произошло бы разделения зарядов, и потенциал все равно не пострадал бы.

.