Формула для нахождения сопротивления проводника: Удельное сопротивление. Реостаты — урок. Физика, 8 класс.

Расчет сопротивления проводника – формула

4.6

Средняя оценка: 4.6

Всего получено оценок: 117.

4.6

Средняя оценка: 4.6

Всего получено оценок: 117.

Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести двумя способами: первый способ заключается в использовании формулы закона Ома, а второй вариант расчета подразумевает знание геометрических размеров проводника и удельного сопротивления вещества, из которого он сделан.

Почему проводник “сопротивляется”?

Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.

В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию.

Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).

Таким образом возникает сопротивление протеканию (нарастанию) тока. Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.

Расчет сопротивления с помощью закона Ома

Немецкий физик Георг Ом в 1826 г. обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I есть величина постоянная:

$ R={U \over I}=const $ (1),

где:

U — напряжение, В;

I — сила тока, А;

R — сопротивление, Ом.

Эту величину стали называть электрическим сопротивлением. Пользуясь этой формулой, можно экспериментально определить величину неизвестного сопротивления.

Рис. 2. Схема измерения напряжения и тока для определения сопротивления участка цепи.

Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Далее, применяя формулу (1), вычисляется значение R.

Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:

$$ 1 Ом = { 1 В\over 1 A} $$

Расчет с помощью удельного сопротивления

Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого необходимо знать дополнительную информацию о проводнике.

Рис. 3. Проводник с поперечным сечением S и длиной L, через который течет ток I.

Георг Ом и другие исследователи опытным путем определили, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника

S. Эту закономерность можно описать формулой расчета сопротивления проводника:

$ R = ρ *{ L\over S} $ (2)

Коэффициент ρ был назван удельным сопротивлением. 2\over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.

Что мы узнали?

Итак, мы узнали, что расчет сопротивления проводника можно произвести двумя способами. Первый расчет проводится с помощью формулы закона Ома после измерения величин напряжения и тока. Для второго расчета необходима информация о геометрических размерах проводника и его удельном сопротивлении.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 117.

---

А какая ваша оценка?

Что такое удельное сопротивление. Расчёт сопротивления проводника

Что это такое

Удельным сопротивлением проводника называется физический вид величины, который показывает, что материал может препятствовать электротоку. По-другому, это такое сопротивление металлов, которое оказывает материал с единичным сечением сопротивление протекающему току. Отличается удельное сопротивление постоянному току тем, что оно вызывается током на проводник. Что касается переменного тока, то он появляется в проводнике под действием вихревого поля.

Важно также уточнить, что собой представляет удельная электрическая проводимость. Электропроводимость — это величина, которая обратна сопротивлению и называется электропроводностью. Это показатель, показывающий меру проводимости силы электротока.

Обратите внимание! Чем больше он, тем лучше способен проводник проводить электричество.

В чем измеряется

Согласно международной системе единиц, измеряется величина в омах, умноженных на метр. В некоторых случаях применяется единица ом, умноженная на миллиметр в квадрате, поделенная на метр. Это обозначение для проводника, имеющего метровую длину и миллиметровую площадь сечения в квадрате.

Формула

Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.

Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.

Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.

Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.

Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:

• олово — 9,9 * 10-8 Ом * мм2/м;
• медь — 0,01724 Ом * мм2/м;
• алюминий — 0,0262 Ом * мм 2/м;
• железо — 0,098 * Ом * мм2/м;
• золото — 0,023 Ом * мм2/м.

Для проводников характерно увеличение сопротивления при росте температуры. Это связано с колебаниями атомов. В то же время с ростом температуры проводимость в полупроводниках и диэлектриках возрастает из-за увеличения концентрации носителей заряда.

Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.

Какие существуют виды

Их немного, одно из которых мы уже разобрали:

• омическое;
• активное;
• индуктивное;
• ёмкостное.

Формулы расчёта электрического сопротивления для переменного тока

К сожалению, наш друг-физик решил не идти нам навстречу и вывел несколько формул по нахождению всех трёх величин. Электрическое сопротивление обозначается буквой R.

Но перед тем как пойти дальше, совет: всегда придумывайте какие-нибудь ассоциации, чтобы запомнилось на всю жизнь, например:

1. R (сопротивление). Можете запомнить что R, как рюмка. Нужно сопротивляться, чтобы не выпить ещё одну рюмку.
2. I (сила тока). Латинская «I», как проводок, по которому идёт ток.
3. U (напряжение). Эта буква, как дуга. И напряжение разносится с одного конца на другой по дуге.

Ну и, конечно, формула закона Ома для участка цепи.

1. R=U/I  т.е., чтобы найти сопротивление(рюмку) надо напряжение (дугу) разделить на ток (проводок).
2. U=IR, хотите найти напряжение (дугу), умножьте проводок на рюмку.
3. I=U/R чтобы найти чему равен проводок, нужно напряжение разделить на сопротивление.

Ну а теперь главное, для чего мы все здесь собрались: «Зачем нужен этот закон? Что он даёт?»

Представьте перед собой электрическую цепь, по которой проходит ток, напряжение и сопротивление. И встаёт вопрос, как понять где что и в каких размерах. Для этого вывели формулу.

Также не забывате, если вдруг вас спросят от чего зависит сопротивление — отвечайте: » От напряжения и мощности».

Активного сопротивления

Ну что сказать? Придется запастись терпением и потратить время на все эти законы и определения.

Но к счастью, активное сопротивление, так и осталось большой буквой R. Просто немного поменялась формула и ее предназначение.

Подключим к нашей цепи проводник. Проводником может выступать лампа.

Понятно, что по нему тоже будет проходить ток. Это как танец «волна». Все 5 человек берутся за руки и начинают по очереди создавать колебания. Сопротивление уже известно на всех. Так же и здесь.

Мы ищем полное сопротивление. Обозначается большой буквой Z.

Если посмотреть, то можно найти сходство танца «волны» с этой буквой. Так и запомните.

Формула, как рассчитать силу тока:

I=U/Z

Индуктивного сопротивления

Боюсь, что когда вы увидите данную формулу, то она вам точно не понравится. Но нет слова «не хочу», есть слово «надо».

Начнем с обозначения:

• XL (индуктивное сопротивление). Прямо как размер в одежде. Но почему именно так? L — это цепь переменного тока;
• f — частота, в Гц;
• сопротивление с частотой взаимосвязаны, так, если возрастает одно — увеличивается и другое;
• единица СИ индуктивного сопротивления: [XL] = Ом;
• запомните, что индуктивное сопротивление отличается от омического тем, что у первого нет потери мощности;
• XL=2π×f×L;
• формула расчета мощности по напряжению: P = U×I;
• мощность электрического тока вычисляется в Ватах.

Емкостного

Ёмкостное сопротивление — это проводник, который подключен к цепи. Он не имеет сопротивление, но есть ёмкость. Обозначается это ёмкостное сопротивление буквами Xc.

Единица измерения сопротивления неизменно остается Ом.

• Xc = 1/ωC;
• ω — циклическая частота;
• С — ёмкость.

Полного

Как говорилось выше — полное сопротиление что-то на подобии танца «волны». Нужно узнать R (сопротивление) всех.

Чтобы определить полное сопротивление цепи:

R = R1 +R2 (проводников может быть несколько).

Теперь, если у вас спросят как определить общее сопротивление цепи, вы знаете что делать.

Нахождение параметра

Найти сопротивление — значит, рассчитать потери тока. Существует 2 принципиально разных подхода к расчёту. В одном случае он ведётся для электрической цепи, а в другой — для материала. Если во втором случае всё предельно понятно, используется одна формула, в которую подставляют размеры тела и табличное значение удельной проводимости, то для электрической цепи не так всё просто.

В цепи может встречаться 3 вида соединения элементов:

1. Параллельное. При таком соединении цепь разветвляется, то есть появляются ветви, по которым течёт ток. Ветви могут пересекаться между собой.
2. Последовательное. Схема соединения представляет единую цепь, в которой нет разветвлений.
3. Смешанное. Состоит из комбинированного соединения, включающего комбинации из параллельного и последовательного подключения.

Вычисление сопротивления для каждого типа соединения имеет особенности. При последовательном включении общее значение определяется путём простого складывания: R = r1 + r2 +…+ rn. При параллельном же соединении полное сопротивление цепи будет меньше самого малого из сопротивлений ветвей. Для такого включения верна формула: 1 / R = 1 / r1 + 1 / r2 +…+ 1 / rn.

Принцип расчёта смешанного соединения построен на группировке электрической цепи по виду подключения элементов. Определение параметра выполняют поочерёдно. Сначала высчитывают сопротивление одного узла, включающего однотипное соединение, затем к результату добавляют следующий элемент. Эту операцию повторяют до тех пор, пока не останется один элемент.

В радиотехнике деталь, применяющуюся в качестве сопротивления, называют резистором. С его помощью обозначают и так называемый эквивалентный параметр, используемый при расчётах электрических цепей. Его вводят, если нужно определить, например, мощность источника тока, выходное напряжение.

Таким образом, чтобы правильно посчитать сопротивление, нужно учитывать несколько факторов. При этом нужно помнить о единой системе измерений. Следует придерживаться СИ. Все величины, используемые в формулах, должны подставляться в стандартных единицах измерения. Почти во всех таблицах значение удельного сопротивления даётся в мм2/м, что связано с измерением площади.

Зависимость удельного сопротивления от температуры

Говоря об удельном сопротивлении, нельзя упомянуть о влиянии температуры окружающей среды на его значение. Однако, это влияние будет разным для каждого материала. Это объясняется одним важным параметром $α$ — температурным коэффициентом.

Температурный коэффициент используется в формула для расчета удельного сопротивления с учетом изменения температуры:

$ρ_t =ρ_0 • [1+α•(t-t_0)]$, где

• $ρ_0$ — удельное сопротивление при 20 С*,
• $α$ — температурный коэффициент,
• $t-t_0$ — разница температур.

Рассчитаем удельное сопротивление меди при -30 C и +30 C .

Пример 1

Для расчета удельного сопротивления при +30 C*, нужно взять первую формулу и подставить известные значения:

$ρ_t=ρ_0 • [1+α•(t-t_0)]=0,017• [1+0,0039•(30-20)]=0,017•[1+(0,0039•10)]=0,0176 $

Для расчета удельного сопротивления при -30 C*, нужно взять вторую формулу и выполнить аналогичный расчет:

$ρ_t=ρ_0 • [1+α•(t-t_0)]=0,017 • [1+(0,0039 • (– 30 – 20)=0,0136$

Исходя из расчетов можно сделать вполне логичный вывод, который заключается в следующем.

Замечание 2

Чем выше температура окружающей среды, тем выше удельное сопротивление.

Связь с удельной проводимостью

В изотропных материалах связь между удельным сопротивлением ρ {displaystyle rho } и удельной проводимостью σ {displaystyle sigma } выражается равенством

ρ = 1 σ . {3}sigma _{ij}({vec {r}})E_{j}({vec {r}}).}

Из этого равенства и приведённого ранее соотношения для E i ( r → ) {displaystyle E_{i}({vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:

ρ 11 = 1 det ( σ ) [ σ 22 σ 33 − σ 23 σ 32 ] , {displaystyle rho _{11}={frac {1}{det(sigma )}}[sigma _{22}sigma _{33}-sigma _{23}sigma _{32}],} ρ 12 = 1 det ( σ ) [ σ 33 σ 12 − σ 13 σ 32 ] , {displaystyle rho _{12}={frac {1}{det(sigma )}}[sigma _{33}sigma _{12}-sigma _{13}sigma _{32}],}

где det ( σ ) {displaystyle det(sigma )} — определитель матрицы, составленной из компонент тензора σ i j {displaystyle sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов.

Формулировка закона

Закон Ома говорит, что сила тока (I) отдельно взятого участка цепи пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.

Следует заметить, что в таком виде закон остается верным только для однородного участка цепи. Однородной называется та часть электрической цепи, которая не содержит источника тока. Как пользоваться законом Ома в неоднородной цепи, будет рассмотрено ниже.

Позже опытным путем было установлено, что закон остается справедливым и для растворов электролитов в электрической цепи.

Что такое ЭДС и откуда она берется

ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.

• ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.

Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.

Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.

В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:

Закон Ома для полной цепи I = ε/(R + r) I — сила тока [A] ε — ЭДС [В] R — сопротивление [Ом] r — внутреннее сопротивление источника [Ом]

Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.

Решим задачу на полную цепь.

Задачка

Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом

Решение:

Возьмем закон Ома для полной цепи:

I = ε/(R + r)

Подставим значения:

I = 4/(3+1) = 1 A

Ответ: сила тока в цепи равна 1 А.

Как образуется сопротивление проводников

Современные воззрения говорят: свободные электроны перемещаются по проводнику со скоростью порядка 100 км/с. Под действием возникающего внутри поля дрейф упорядочивается. Скорость перемещения носителей вдоль линий напряженности мала, составляет единицы сантиметров в минуту. В ходе движения электроны сталкиваются с атомами кристаллической решетки, некая доля энергии переходит в тепло. И меру этого преобразования принято называть сопротивлением проводника. Чем выше, тем больше электрической энергии переходит в тепло. На этом основан принцип действия обогревателей.

Параллельно контексту идет численное выражение проводимости материала, которое можно увидеть на рисунке. Для получения сопротивления полагается единицу разделить на указанное число. Ход дальнейших преобразований рассмотрен выше. Видно, что сопротивление зависит от параметров – температурное движение электронов и длина их свободного пробега, что прямо приводит к строению кристаллической решётки вещества. Объяснение – сопротивление проводников отличается. У меди меньше алюминия.

Когда «сопротивление бесполезно»

Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.

А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.

Ток идет по пути наименьшего сопротивления.

Теперь давайте посмотрим на закон Ома для участка цепи еще раз.

Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом]

Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.

То есть:

I = U/0 = ∞

Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.

Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.

Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.

Катушка индуктивности

Катушки индуктивности представляет собой устройство, главной частью которого является проводящий металл, скрученный в некое подобие колец либо обернутый вокруг диэлектрического сердечника. Если через такое устройство проходит электрический ток, то формируется местное магнитное поле. Это происходит из-за концентрации переменного магнитного поля.

Для вычислительной техники используется дроссель, который применяется для питания различного высокоточного оборудования. Устройство требуется для снижения колебаний переменного напряжения. С добавлением частоты сопротивление соответственно увеличивается. Технические параметры дросселя зависят от площади поперечного сечения проводящего материала, числа витков вокруг сердечника из диэлектрика.

Электросопротивление других металлов

Кроме меди и алюминия, в электротехнике используются другие металлы и сплавы:

• Железо. Удельное сопротивление стали выше, но она прочнее, чем медь и алюминий. Стальные жилы вплетаются в кабеля, предназначенные для прокладки по воздуху. Сопротивление железа слишком велико для передачи электроэнергии, поэтому при расчёте сечения жилы не учитываются. Кроме того, оно более тугоплавкое, и из него изготавливаются вывода для подключения нагревателей в электропечах большой мощности;
• Нихром (сплав никеля и хрома) и фехраль (железо, хром и алюминий). Они обладают низкой проводимостью и тугоплавкостью. Из этих сплавов изготавливаются проволочные резисторы и нагреватели;
• Вольфрам. Его электросопротивление велико, но это тугоплавкий металл (3422 °C). Из него изготавливаются нити накала в электролампах и электроды для аргонно-дуговой сварки;
• Константан и манганин (медь, никель и марганец). Удельное сопротивление этих проводников не меняется при изменениях температуры. Применяются в претензионных приборах для изготовления резисторов;
• Драгоценные металлы – золото и серебро. Обладают самой высокой удельной проводимостью, но из-за большой цены их применение ограничено.

Материалы высокой проводимости

К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10-20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).

Медь

Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:

1. малое удельное сопротивление;
2. достаточно высокая механическая прочность;
3. удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
4. хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
5. относительная легкость пайки и сварки.

Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.

В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0.05% примесей, в том числе не свыше 0.02% кислорода.

Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.

В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.

Алюминий

Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного — 2.7 Мг/м3. Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.

Алюминий обладает пониженными по сравнению с медью свойствами — как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.

Для электротехнических целей используют алюминий, содержащий не более 0. 5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.

Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.

Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg2Si, которое сообщает высокие механические свойства сплаву.

Железо и сталь

Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.

В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.

Натрий

Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2. 8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.

Пример из практики

Последовательно с источником освещения включен тестер. Напряжение осветительного прибора = 220 Вольт. Мощность неизвестна. На показателе амперметра указано 276 миллиампер тока. Какая величина у спирали лампы при последовательном включении в схему резисторов?

Формула нахождения сопротивления спирали

Электросопротивление представляет собой физическую величину, которая соответствует степени препятствия движению электрических частиц у каждого материала. Возможно измерить уровень величины мультиметром. В таком случае придется находить значение по формуле. Для предотвращения попадания электрического тока на непредназначенные для этого участки желательно заземлять линии передачи. Данная физическая величина используется во многих радиодеталях, например, светодиодах. В электрической цепи, чтобы узнать величину, требуется подключить к вольтметру фазу и ноль при известной силе тока, затем рассчитать по закону Ома.

Источники

• https://rusenergetics.ru/ustroistvo/udelnoe-soprotivlenie
• https://hmelectro.ru/poleznye_statyi/chto-takoe-soprotivlenie
• https://nauka.club/fizika/raschyet-soprotivleniya-provodnik%D0%B0.html
• https://tokzamer.ru/informaciya/formula-elektricheskogo-soprotivleniya-dlya-novichkov
• https://master-pmg.ru/cvetmet/kak-najti-udelnoe-soprotivlenie.html
• https://skysmart.ru/articles/physics/zakon-oma
• https://amperof.ru/elektroenergia/soprotivlenie-toka-formula.html
• https://PlazmoSvarka. ru/metally/soprotivlenie-medi.html

[свернуть]

15.3 Сопротивление и удельное сопротивление – Физика Колледжа Дугласа 1104 Индивидуальный учебник – зима и лето 2020

Глава 15 Электрический ток, сопротивление и закон Ома

Резюме

• Объясните понятие удельного сопротивления.
• Используйте удельное сопротивление для расчета сопротивления определенных конфигураций материала.
• Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.

Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рис. 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра [латекс]\boldsymbol{R}[/латекс] прямо пропорционально его длине [латекс]\жирный символ{L}[/латекс], аналогично сопротивлению трубы потоку жидкости.

. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле, [латекс]\boldsymbol{R}[/латекс] обратно пропорциональна площади поперечного сечения цилиндра [латекс]\жирный символ{А}[/латекс].

Рисунок 1. Однородный цилиндр длиной L и площадью поперечного сечения A . Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения A , тем меньше его сопротивление.

Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Мы определяем

удельное сопротивление  [латекс]\boldsymbol{\rho}[/латекс] вещества, так что сопротивление  [латекс]\жирныйсимвол{R}[/латекс] объекта прямо пропорционально [латекс]\жирныйсимвол{ \ро}[/латекс]. Удельное сопротивление [латекс]\boldsymbol{\rho}[/латекс] — это внутреннее свойство материала, не зависящее от его формы или размера. Сопротивление [латекс]\boldsymbol{R}[/латекс] однородного цилиндра длиной [латекс]\boldsymbol{L}[/латекс], площадью поперечного сечения [латекс]\boldsymbol{A}[/латекс] , и изготовлен из материала с удельным сопротивлением [латекс]\boldsymbol{\rho}[/латекс], составляет

[латекс]\boldsymbol{R =}[/латекс] [латекс]\boldsymbol{\frac{\rho L}{A}}[/латекс].

В таблице 1 приведены репрезентативные значения [латекс]\жирныйсимвол{\ро}[/латекс]. Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы – наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться.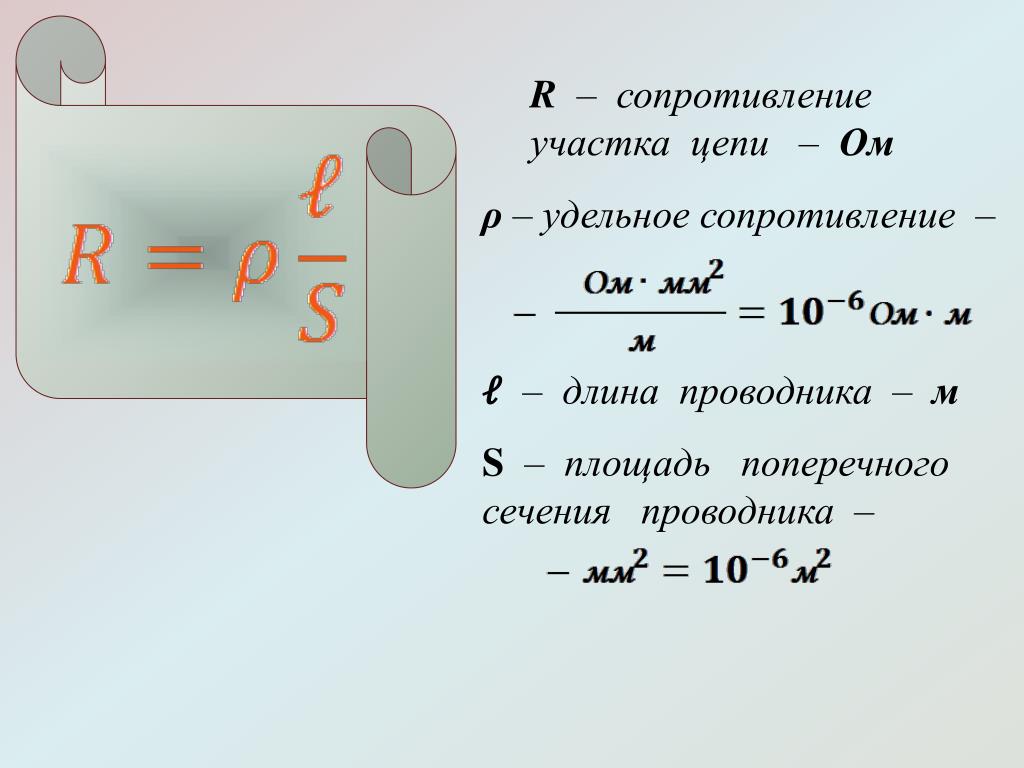

Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах. 9{11}}[/латекс] Таблица 1. Удельное сопротивление [латекс]\boldsymbol{\rho}[/латекс] различных материалов при 20ºC

Пример 1. Расчет диаметра резистора: нить накала фары

Нить накала автомобильной фары изготовлена ​​из вольфрама и имеет морозостойкость [латекс]\boldsymbol{0,350 \;\Omega}[/латекс]. Если нить представляет собой цилиндр длиной 4,00 см (можно свернуть в спираль для экономии места), то каков ее диаметр?

Стратегия

Мы можем преобразовать уравнение [латекс]\boldsymbol{R = \frac{\rho L}{A}}[/latex], чтобы найти площадь поперечного сечения [латекс]\boldsymbol{A}[/latex] нить из предоставленной информации. Тогда его диаметр можно найти, предполагая, что он имеет круглое поперечное сечение.

Решение

Площадь поперечного сечения, полученная перестановкой выражения сопротивления цилиндра, приведенного в [латекс]\жирный символ{R = \frac{\rho L}{A}}[/latex],

[латекс]\boldsymbol{A =}[/латекс] [латекс]\boldsymbol{\frac{\rho L}{R}}[/латекс] 9{-5} \;\textbf{m}} \end{array}.[/latex]

Обсуждение

Диаметр чуть меньше одной десятой миллиметра. Он заключен в кавычки только до двух цифр, потому что [латекс]\жирныйсимвол{\ро}[/латекс] известен только до двух цифр.

Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.) И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC или меньше) удельное сопротивление [латекс]\boldsymbol{\rho}[/латекс] зависит от изменения температуры [латекс]\жирныйсимвол{\Delta T}[/латекс], как это выражается в следующем уравнении

[латекс]\boldsymbol{ \rho = \rho_{0} (1 + \alpha \Delta T)},[/latex]

, где [latex]\boldsymbol{\rho_0}[/latex] — исходное удельное сопротивление, а [latex]\boldsymbol{\alpha}[/latex] — температурный коэффициент удельного сопротивления . (См. значения [латекс]\жирныйсимвол{\альфа}[/латекс] в таблице 2 ниже.) Для больших изменений температуры [латекс]\жирныйсимвол{\альфа}[/латекс] может меняться, или нелинейное уравнение может быть нужно найти [латекс]\boldsymbol{\rho}[/латекс]. Обратите внимание, что [латекс]\жирныйсимвол{\альфа}[/латекс] положителен для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость.

Манганин (состоящий из меди, марганца и никеля), например, имеет [латекс]\boldsymbol{\alpha}[/латекс] близок к нулю (до трех цифр по шкале в таблице 2), поэтому его удельное сопротивление лишь незначительно зависит от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем увеличивается почти линейно с температурой. 9{-3}}[/латекс]

Таблица 2: Температурные коэффициенты удельного сопротивления [латекс]\boldsymbol{\alpha}[/латекс]

Отметим также, что [латекс]\жирныйсимвол{\альфа}[/латекс] имеет отрицательное значение для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения [латекса] \boldsymbol{\rho}[/латекса] с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.

Сопротивление объекта также зависит от температуры, так как [латекс]\boldsymbol{R_0}[/латекс] прямо пропорционально [латекс]\жирныйсимвол{\ро}[/латекс]. Для цилиндра мы знаем [латекс]\boldsymbol{R = \rho L/A}[/latex], и поэтому, если [латекс]\boldsymbol{L}[/латекс] и [латекс]\boldsymbol{A}[ /латекс] не сильно меняются с температурой, [латекс]\boldsymbol{R}[/латекс] будет иметь ту же температурную зависимость, что и [латекс]\жирныйсимвол{\rho}[/латекс]. (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на [латекс]\boldsymbol{L}[/латекс] и [латекс]\boldsymbol {A}[/latex] примерно на два порядка меньше, чем на [latex]\boldsymbol{\rho}[/latex]. ) Таким образом,

[латекс]\boldsymbol{R = R_0(1 + \alpha \Delta T)}[/латекс]

— зависимость сопротивления объекта от температуры, где [latex]\boldsymbol{R_0}[/latex] — исходное сопротивление, а [latex]\boldsymbol{R}[/latex] — сопротивление после изменения температуры [ латекс]\boldsymbol{\Delta T}[/латекс]. Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Рисунок 3. Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. (кредит: Biol, Wikimedia Commons)

Пример 2: Расчет сопротивления: сопротивление горячей нити

Хотя следует соблюдать осторожность при применении [латекс]\boldsymbol{ \rho = \rho_0(1 + \alpha \Delta T)}[ /latex] и [latex]\boldsymbol{R = R_0(1 + \alpha \Delta T)}[/latex] для изменений температуры более 100ºC, для вольфрама уравнения работают достаточно хорошо при очень больших изменениях температуры. Каково же тогда сопротивление вольфрамовой нити в предыдущем примере, если ее температуру повысить с комнатной (20°С) до типичной рабочей температуры 2850°С? 9{\circ}C)]} \\[1em] & \boldsymbol{4.8 \;\Omega} \end{array}.[/latex]

Обсуждение

Это значение согласуется с примером сопротивления фары в Пример 1 Глава 20.2 Закон Ома: сопротивление и простые цепи.

Исследования PhET: сопротивление в проводе

Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.

Рис. 4. Сопротивление в проводе

• Сопротивление [латекс]\boldsymbol{R}[/латекс] цилиндра длиной [латекс]\boldsymbol{L}[/латекс] и площадью поперечного сечения [латекс]\boldsymbol{A}[/латекс] [латекс]\boldsymbol{R = \frac{\rho L}{A}}[/latex], где [латекс]\boldsymbol{\rho}[/латекс] — удельное сопротивление материала.
• Значения [латекс]\жирныйсимвол{\rho}[/латекс] в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .
• Температура влияет на удельное сопротивление; для относительно небольших изменений температуры [латекс]\boldsymbol{\Delta T}[/latex], удельное сопротивление равно [латекс]\boldsymbol{\rho = \rho_0(1 + \alpha \Delta T)}[/latex], где [ латекс]\boldsymbol{\rho_0}[/латекс] — исходное удельное сопротивление, а αα — температурный коэффициент удельного сопротивления.
• В таблице 2 приведены значения [латекс]\жирныйсимвол{\альфа}[/латекс], температурный коэффициент удельного сопротивления.
• Сопротивление [латекс]\boldsymbol{R}[/латекс] объекта также зависит от температуры: [латекс]\жирный символ{R = R_0(1 + \alpha \Delta T)}[/латекс], где [латекс ]\boldsymbol{R_0}[/latex] — исходное сопротивление, а [latex]\boldsymbol{R}[/latex] — сопротивление после изменения температуры.

Задачи и упражнения

1: Чему равно сопротивление отрезка медной проволоки 12-го калибра диаметром 2,053 мм длиной 20,0 м?

2: Диаметр медной проволоки 0-го калибра 8,252 мм.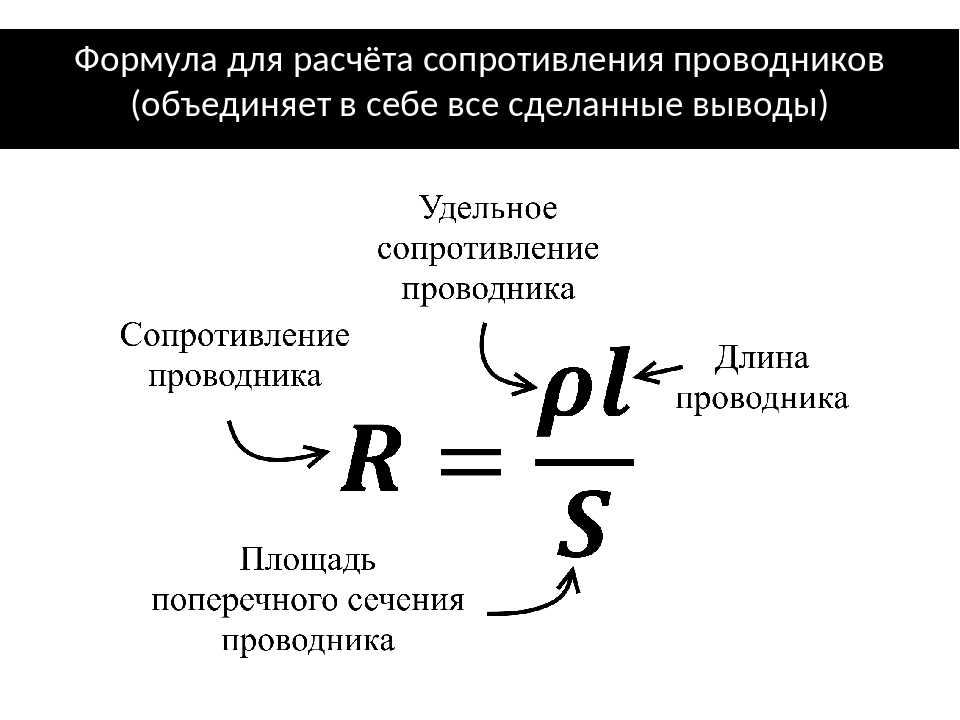 Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.

3: Если вольфрамовая нить диаметром 0,100 мм в лампочке должна иметь сопротивление [латекс]\boldsymbol{0,200 \;\Омега}[/латекс] при 20,0ºC, какой длины она должна быть? 93 \;\textbf{V}}[/latex] применяется к нему? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц). в габаритах? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?

7: Резистор из нихромовой проволоки используется в тех случаях, когда его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?

8: Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?

9: Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит чисто углеродные резисторы. Во сколько раз увеличивается их сопротивление в этом диапазоне?

10: (а) Из какого материала изготовлена ​​проволока, если она имеет длину 25,0 м, диаметр 0,100 мм и сопротивление [латекс]\boldsymbol{77,7 \;\Омега}[/латекс] при 20,0ºС? б) Каково его сопротивление при 150°С?

11: При постоянном температурном коэффициенте удельного сопротивления, каково максимальное уменьшение сопротивления константановой проволоки в процентах, начиная с 20,0ºC?

12: Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной. Во сколько раз увеличивается его сопротивление?

13: Медная проволока имеет сопротивление [латекс]\boldsymbol{0,500 \;\Омега}[/латекс] при 20,0ºC, а железная проволока имеет сопротивление [латекс]\boldsymbol{0,525 \; \Omega}[/latex] при той же температуре. При какой температуре их сопротивления равны? 9{\circ} \textbf{C}}[/latex]), когда он имеет ту же температуру, что и пациент. {\circ} \textbf{C}}[/латекс]. б) На сколько процентов ваш ответ отличается от ответа в примере?

16: Необоснованные результаты

(a) До какой температуры нужно нагреть резистор, сделанный из константана, чтобы удвоить его сопротивление при постоянном температурном коэффициенте удельного сопротивления? б) Разрезать пополам? в) Что неразумного в этих результатах? (d) Какие предположения неразумны, а какие предпосылки противоречивы?

Сноски

1. 1 Значения сильно зависят от количества и типов примесей
2. 2 Значения при 20°C.

Глоссарий

Удельное сопротивление

внутреннее свойство материала, независимое от его формы или размера, прямо пропорциональное сопротивлению, обозначаемому ρ

температурный коэффициент удельного сопротивления

эмпирическая величина, обозначаемая α , которая описывает изменение сопротивления или удельного сопротивления материала при изменении температуры

Формула электрического сопротивления

0001

Когда к любому проводнику приложено напряжение, электрические заряды начинают течь по проводнику, и скорость потока заряда называется током. Свойство материалов, которое измеряет количество протекающего через него заряда, известно как электрическое сопротивление, а также на основе которого материалы классифицируются как хорошие или плохие проводники электричества.

Электрическое сопротивление

Электрическое сопротивление является свойством использования, мы выделяем тепло и имеем различные применения в нашей повседневной жизни.

Электрическое сопротивление: Свойство электрического проводника противодействовать (сопротивляться) потоку электрического тока известно как электрическое сопротивление . Все материалы имеют собственное электрическое сопротивление. Он представлен R , а его единица СИ равна Ом Ω (греческая буква Омега)

Георг Симон Ом был немецким физиком, который вывел закон, известный как закон Ома, а также дает связь между током, напряжением и сопротивление. Согласно закону Ома, сила тока, протекающего через проводник, прямо пропорциональна разности потенциалов на нем.

В ∝ I

или

В = IR

Таким образом, из приведенных выше уравнений получаем соотношение:

R = V/I 9001 9

где

• В – разность потенциалов на проводнике (в вольтах),
• I — ток через проводник (в амперах), а
• R — константа пропорциональности, называемая сопротивлением (в омах).

Удельное электрическое сопротивление (удельное сопротивление)

Удельное электрическое сопротивление или удельное сопротивление — это фундаментальное свойство материала, которое измеряет, насколько сильно он сопротивляется электрическому току. Низкое удельное сопротивление указывает на то, что материал легко пропускает электрический ток. Удельное сопротивление определяется как сопротивление, предлагаемое материалом на единицу длины для единицы поперечного сечения, и обратно пропорционально сопротивлению.

• Удельное сопротивление обычно обозначается греческой буквой ρ (ро).
• Единицей удельного электрического сопротивления в системе СИ является ом-метр (Ом-м) или мОм.

Математически удельное сопротивление определяется как

, где

• R — сопротивление ,
• L — длина,
• A — площадь поперечного сечения проводника.

Из приведенного выше соотношения видно, что сопротивление проводника зависит от следующих факторов:

1. Площадь поперечного сечения проводника
2. Длина проводника
3. Материал проводника
4. Температура проводящего материала

Материалы с низким значением удельного электрического сопротивления очень хорошо проводят электричество, являются проводниками и изоляторами будет иметь более высокое значение удельного сопротивления, чем у проводников. Некоторые материалы и их стандартное удельное сопротивление (УЭС) при 20° ^C:

902 53

Материал	Удельное сопротивление (в Ом·м)
Алюминий	2,8 × 10 -8
Медь	1,7 × 10 -8
Золото	2,4 × 10 -8 9000 5
Углерод (графит)	1 × 10 -5
Германий	9000 2 4,6 × 10 -1
Железо	1,0 × 10 – 7
Свинец	1,9 × 10 -7
Нихром	1,1 × 10 -6
Серебристый	1,6 × 10 -8

Следовательно, две важные формулы для электрического сопротивления выглядят следующим образом:

• R = V/I
• R = (ρ×L)/A

где R — сопротивление, V — напряжение, I — ток, ρ — удельное сопротивление, L — длина, а A — поперечное сечение площадь проводника.

Примеры задач на электрическое сопротивление

Задача 1. Каково сопротивление цепи, в которой приложено напряжение 12 В, а через нее протекает ток 4 А?

Решение:

Согласно соотношению:

V = IR

или

R = V/I

Следовательно,

R = 12 В/4 А

R = 3 Ом

Задача 2: Какой ток протекает в цепи, в которой приложенное напряжение равно 12 В, а сопротивление проводника равно 3 Ом?

Решение:

Согласно соотношению:

V = IR 

или 

I = V/R

Отсюда следует, 9000 5

I = 12 В/3 Ом

I = 4 A

Задача 3. Какое напряжение приложено к цепи, в которой ток, проходящий через проводник, равен 4 А, а сопротивление проводника равно 3 Ом?

Решение:

Согласно соотношению: 912 В и площадь пересечения секция 10 ^-6 м ² .