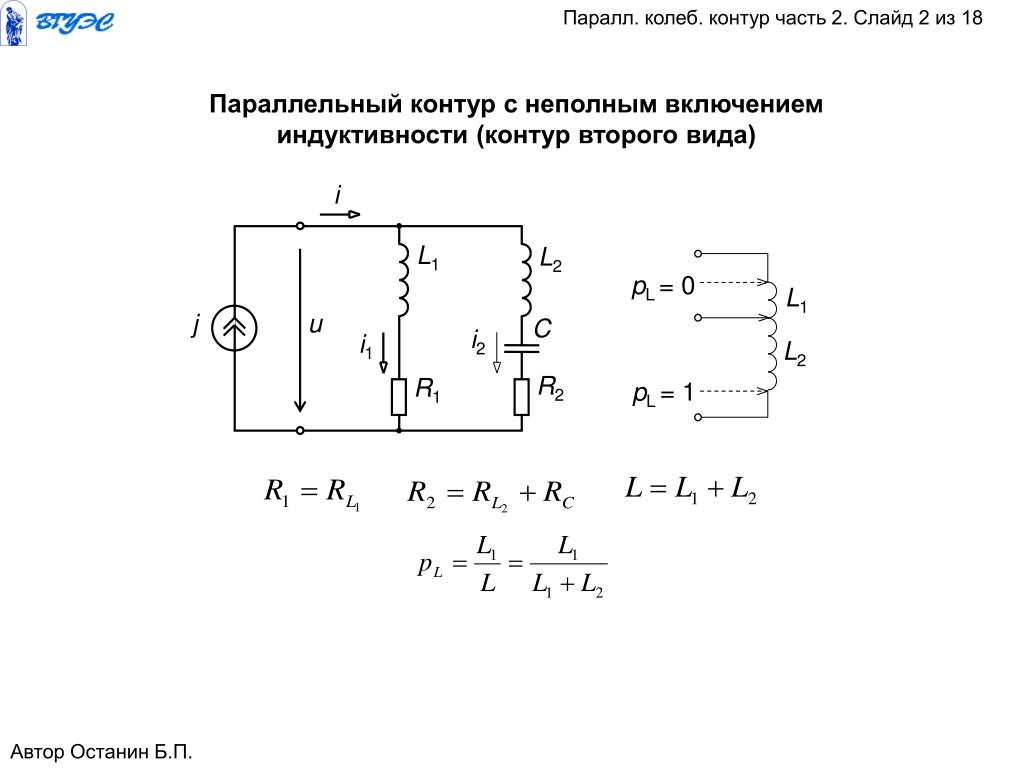
Расчёт электрической цепи постоянного тока методом наложения (суперпозиции токов)
Этот метод заключается в том, что воздействие нескольких источников на какой либо элемент цепи можно рассматривать как результат воздействия на элемент каждой ЭДС по отдельности независимо от других источников.
Если в рассчитываемой цепи присутствует несколько источников ЭДС, то расчет электрической цепи сводится к расчету нескольких цепей с одним источником. Ток в любой ветви рассматривается как алгебраическая сумма частных токов созданных каждой ЭДС по отдельности.
Рассмотрим метод наложения на примере данной схемы рисунок 1.
Дано:
E1=100 B, E2=50 B; R1=4 Om, R2=10 Om; R3=12 Om, r01=1Om, r02=2 Om.
Найти: Все токи.
Порядок расчета:
- Определяем количество источников в схеме.
- Предположим, что в цепи действует только Е1 рисунок 2. Укажем на этой схеме направление частных токов создаваемые источником Е1 (токи обозначим с одним штрихом I’1; I’2: I’3). Обратите внимание, если у источника (E1; E2) есть внутреннее сопротивление (r01; r02), то при исключения данного источника его внутренне сопротивление остоётся в схеме.
- Найдем ток I’1. Rэкв — сопротивление всей цепи.
- Найдем ток I’2; I’3 по формуле разброса токов.
- Мы нашли все частные токи в первой схеме (рисунок 2).
- Рассмотрим вторую схему без E1, но с E2 (рисунок 3). Укажем на этой схеме направление частных токов создаваемые источником Е2 (токи обозначим с двумя штрихами I»1; I»2: I»3)
- Найдем ток I»2. RЭКВ рассчитываем заново.

- Найдем токи I»1; I»3 по формуле разброса токов.
- Мы нашли все частные токи для второй схемы (рисунок 3).
- Найдем действующие токи в изначальной схеме (рисунок 1) путем алгебраического сложения частных токов первой (рисунок 2) и второй (рисунок 3) схемы. Для этого смотрим как направлены токи в одинаковых ветвях на рисунке 2 и 3. Если токи направлены в одном направлении, то тогда они складываются, а если токи направлены в разные стороны тогда отнимаем.
- Если конечные токи получаются положительные, то токи направлены так же как на рисунке 2, а если токи получились отрицательными, то тогда они направлены так же как на рисунке 3.
- Правильность решения можно проверить при помощи баланса мощности.
ТОЭ Гилицкая, Расчет линейных электрических цепей постоянного тока (ч1) – dump – Каталог статей
Расчет линейных электрических цепей постоянного тока.(ч1)
Заказать решение>
Вариант 0. Сх 1.1. Для электрической цепи, изображенной на рисунке, выполнить следующее:
Сх 1.1. Для электрической цепи, изображенной на рисунке, выполнить следующее:
- Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы.
- Определить токи во всех ветвях схемы, используя метод контурных токов.
- Определить токи во всех ветвях схемы на основании метода наложения.
- Составить баланс мощностей для заданной схемы.
- Результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить.
- Определить ток во второй ветви методом эквивалентного генератора.
- Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Дано:
Определить:
1. Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы.
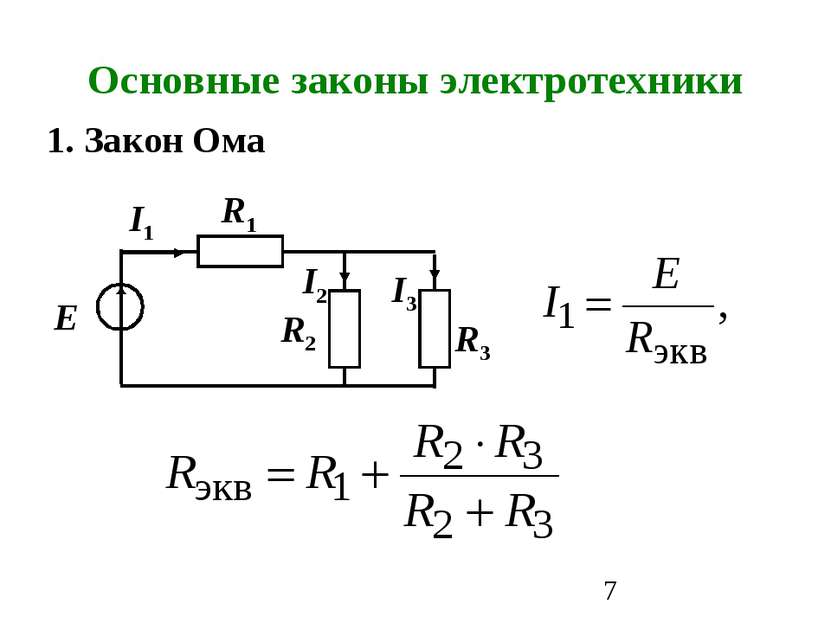
Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи. При расчете данным методом произвольно задаем направление токов в ветвях. Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей.
При расчете данным методом произвольно задаем направление токов в ветвях. Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей.
В заданной цепи шесть ветвей, значит, в системе должно быть шесть уравнений. Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n-1) независимых уравнений. В нашей цепи четыре узла А, Б, В, Г, значит, число уравнений: n-1=4-1=3. Составляем три уравнения для любых 3-х узлов, например, для узлов А, Б и В.
Узел А:
Узел Б:
Узел В:
Всего в системе должно быть шесть уравнений, Три уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие.
Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.
Контур АВБА – обход против часовой стрелки
Контур АГВА – обход против часовой стрелки
Контур БГАБ – обход против часовой стрелки
ЭДС в контуре берется со знаком “+”, если направление ЭДС совпадает с обходом контура, если не совпадает “–“ знак. Падение напряжения на сопротивлении контура берется со знаком “+”, если направление тока в нем совпадает с обходом контура, со знаком “-“, если не совпадает.
Падение напряжения на сопротивлении контура берется со знаком “+”, если направление тока в нем совпадает с обходом контура, со знаком “-“, если не совпадает.
Мы получили систему из шести уравнений с шестью неизвестными:
Решив систему, определим величину и направление тока во всех ветвях схемы. Если при решении системы ток получается со знаком “-“ значит его действительное направление обратно тому направлению, которым мы задались.
2. Определить токи во всех ветвях схемы, используя метод контурных токов
Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1. Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной.
Итак, в заданной цепи можно рассмотреть три контура-ячейки (АВБА, АГВА, БГАБ) и ввести для них контурные токи . Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.
В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.
На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим.Стрелками указываем выбранные направления контурных токов в контурax-ячейках. Направление обхода контуров принимаем таким же. Составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.
Подставляем в уравнение численные значения ЭДС и сопротивлений.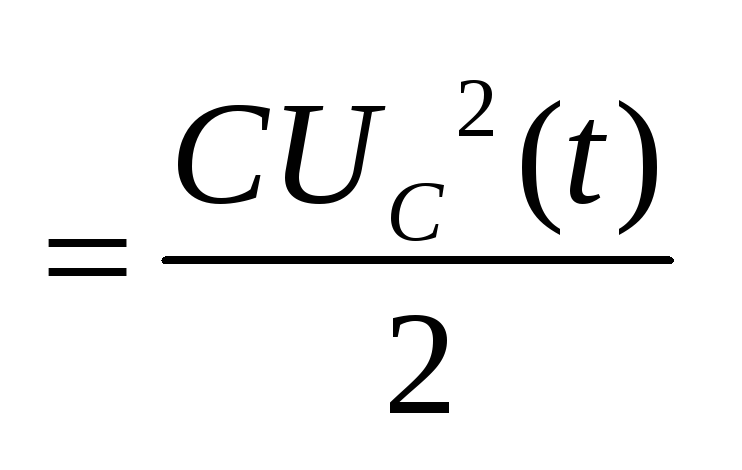
Или
Решим систему с помощью определителей. Вычислим определитель системы и частные определители .
Вычисляем контурные токи:
Действительные токи ветвей:
3. Определить токи во всех ветвях схемы на основании метода наложения;
По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности
а) Определяем частные токи от ЭДС при отсутствии ЭДС .
Показываем направление частных токов от ЭДС и обозначаем буквой I с одним штрихом (I’). Для вычисления токов необходимо выполнить преобразование треугольника АВГ в эквивалентную звезду. Где
Ток источника:
Применяя формулу разброса и первый закон Кирхгофа, вычисляем токи:
Заземлим точку В, ее потенциал равен нулю , тогда:
б) Определяем частные токи от ЭДС при отсутствии ЭДС .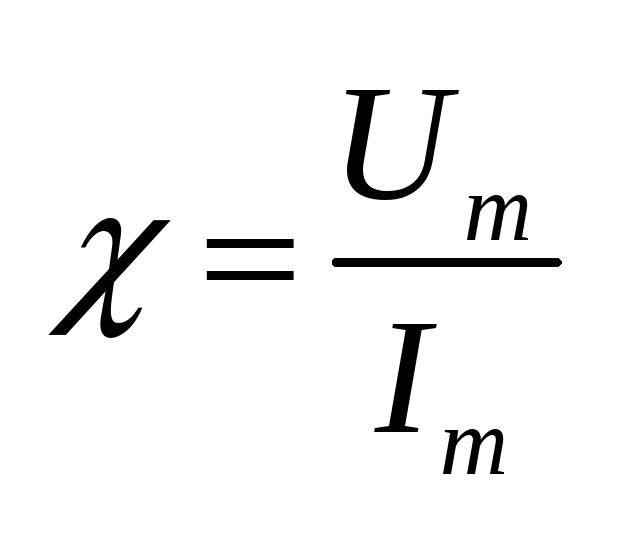
Показываем направление частных токов от ЭДС и обозначаем буквой I с двумя штрихами (I”). Для вычисления токов необходимо выполнить преобразование треугольника АБВ в эквивалентную звезду. Где
Ток источника:
Применяя формулу разброса и первый закон Кирхгофа, вычисляем токи:
Заземлим точку Б, ее потенциал равен нулю , тогда:
в) Вычисляем токи ветвей исходной цепи, выполняя алгебраическое сложение частных токов, учитывая их направление
Продолжение>
как найти R0 в электротехнике
ответы Mail Ru электротехника задача дано е 75в R0 1ом
596 теоретические основы электротехники сборник задач
ответы Mail Ru здравствуйте задача по электротехнике кто
линейные электрические цепи постоянного тока презентация
как найти R0 электротехника расчет электрических цепей
электротехника известна сила тока I3 1 2 а найти
помогите решить задачу по электротехнике E 12br1 1 6комr2
примеры решения задач по теоретическим основам
основные формулы электрика основные формулы в
596 теоретические основы электротехники сборник задач
что такое эдс в электротехнике портал по безопасности
как найти F в электротехнике электротехнические расчетные
электротехника известна сила тока I3 1 2 а найти напряжение U
григораш о в шевченко а а бегдай с н электротехника и
7781 1586 электротехника и электроника ч 1 р р рµрєс
конспект лекций по курсу электроснабжение с основами
примеры решения задач по теоретическим основам
электрическое сопротивление википедия
электротехника и электроника
курсавой высоковольтная электротехника
сборник задач по электротехнике и электронике
Calaméo Ehlektrotekhnika I Osnovy Ehlektroniki Uchebno
двухполюсники электротехника
электротехника и электроника часть 1 линейные и нелинейные
контрольная работа по электротехнике и электронике страница 3
линейные электрические цепи постоянного тока презентация доклад
лабораторная работа по электротехнике и электронике сдать
тоэ лекции 1 электрическая цепь и ее элементы
электротехника электротехника портал искусственного
контрольная работа по электротехнике и электронике стр 3
Treating Skin With Use Of Electroporation тема научной
основы электротехники расчет электрических цепей
1 электрическая цепь ее преобразование
курсовая работа по тоэ Docsity
электротехника расчёт схемы и баланс мощностей
контрольно оценочные средства электротехника
некоторые формулы электротехники документ
юлия валерьевна щербакова электроника и электротехника
температурный коэффициент сопротивления школа для
лушникова е н электротехника и промышленная электроника
сборник задач и упражнений по электротехнике и основам
символьные вычисления
596 теоретические основы электротехники сборник задач
система электроснабжения привязных необитаемых подводных
общая электротехника и электроника
физика задачи на мощность электрического тока ответы и
задачи по электротехнике метод узловых потенциалов
задачи по электротехнике
источники эдс напряжения и источники тока теория
1 электрическая цепь ее преобразование
помогите решить задачу по электротехнике молодежный
электротехника электротехника портал искусственного
электротехника нахождение внутреннего сопротивления и эдс
кафедра энергетики краткий конспект лекций по электротехнике
формула разброса электрикам
Iaне изменится
7 закон ома
Finite Element Technique For Solution Of Thermo Contact
сборник задач по тоэ Freedomcloud
решение задач по электротехнике тоэ другое пример 05
расчет простых цепей постоянного тока
электротехника
дано R1 1om R2 2om R3 4om R4 3om найти R0 параллельное
основные формулы электрика основные формулы в
расчет сложных цепей при помощи уравнений кирхгофа
электротехника и электроника Pdf Free Download
курсовая работа по тоэ Docsity
задачи по тоэ примеры решения задач по теоретическим
методические указания по выполнению лабораторных работ по
общая электротехника и электроника
последовательное и параллельное соединение сопротивлений
электроника и связь
Untitled
пифагор задачи по электротехнике цепи постоянного тока
метод узлового напряжени
линейные электрические цепи постоянного тока презентация доклад
обоснование и повышение энергетических показателей
электрические цепи основные понятия и определения Kievuz
определение и значение электротехники портал по безопасности
Doc электротех марина лагнюк Academia Edu
лабораторная работа по электротехнике и электронике Fiziku5 Ru
физика задачи на мощность электрического тока ответы и
электротехника и электроника часть 1 линейные и нелинейные
теоремы электротехники
оп 03 электротехника и электронная техника Pdf
закон ома для полной цепи Dc
сборник задач по электротехнике учебно методическое пособие
контрольная работа по электротехнике и электронике страница 4
электротехника и электроника
последовательное и параллельное соединения проводников
радиоэлектроника для начинающих и не только Fb2 куллиб
задачи по электротехнике метод узловых потенциалов
методы расчета электрических цепей постоянного тока
электротехника и электроника
Untitled
горная электротехника курсовая работа т геология 2013 03 20
автор составитель к т н доцент контент платформа
реферат теоретические основы электротехники Xreferat Com
напряжение ток мощность формула мощность электрического
диагностика линейных электрических цепей по частям
Нормы на перекос фаз
Перекос фаз явление в электротехнике встречающееся довольно часто.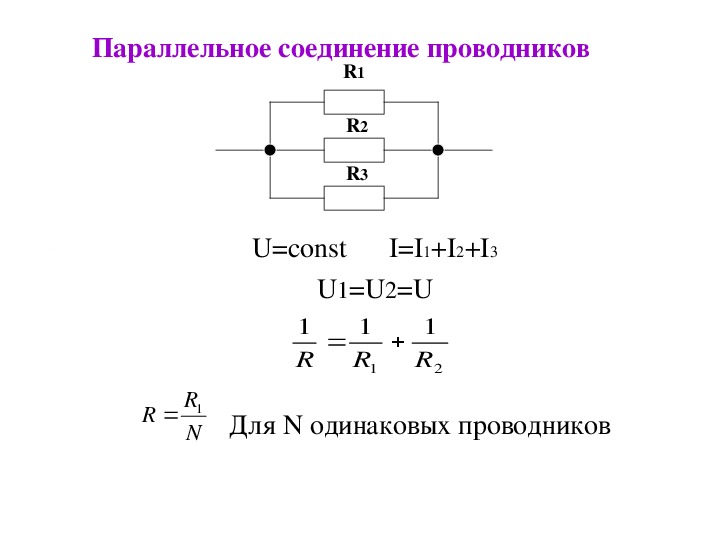
Кабельная линия, проверка на перекос фаз
Сначала давайте определимся в терминах. Речь идет о разнице напряжений, между фазами в трехфазной сети или фазными и нулевым проводником в той же трехфазной цепи. Под перекосом мы будем понимать различие этих напряжений.
Напомним, что любая трехфазная цепь может быть выполнена с «глухо заземлённой нейтралью» либо с «изолированной нейтралью». Первая имеет три фазных проводника и, так называемый, нулевой провод. Вторая только три фазных проводника. Соответственно, потребители в первой цепи могут быть соединены как в треугольник, так и на звезду. Во второй только в треугольник. В сети 380/220 В с глухо заземлённой нейтралью потребители, в подавляющем большинстве случаев, подключены по схеме «звезда». Это относится как к асинхронным двигателям, так и к «осветительным нагрузкам». О таких случаях мы будем вести речь в дальнейшем.
Так называемый перекос фаз, является отклонением от нормальной разницы между мгновенными значениями линейных напряжений, либо результатом изменения фазового угла между линейными напряжениями. Последний случай можно исключить из рассмотрения, так как он встречается крайне редко.
Когда мы определились с терминами можно перейти к рассмотрению вопроса по существу. И тут становиться всё просто. Предположим, что все нагрузки у нас осветительные. Под этим термином понимают активные нагрузки, например в виде ламп накаливания. Ещё, предположим, что к одной из фаз подключено лампочек значительно больше чем к остальным. Токи, протекающие через них, по законам Кирхгофа будут протекать не только через нулевой проводник но, и через других потребителей. В результате падение напряжения на потребителях других фаз неизбежно вырастет. Это и вызывает перекос фаз.
Это и вызывает перекос фаз.
Щит электрический, питающий кабель, проверка на перекос фаз
Все это можно объяснить и через напряжения. Большой ток одной из фаз создает небольшое, но вполне реальное падение напряжения в нулевом проводе. Это напряжение сдвинуто на угол 120о относительно других фаз. Поэтому напряжение, приложенное к их нагрузкам, является суммой фазного напряжения и напряжения на нулевом проводе.
Крайним случаем перекоса фаз является однофазное замыкание на «землю». В этом случае токи короткого замыкания будут протекать и через потребителей, питающихся от двух других фаз что, неизбежно, вызовет перенапряжение в них.
Ещё одним из случаев того же порядка является обрыв нулевого провода. При этом также нарушается баланс токов в нагрузках. Напряжения в сети могут изменяться крайне непредсказуемо, в зависимости от величины нагрузки на каждую из фаз. Практики знают, что напряжения в бытовых розетках, в этих условиях могут достигать даже линейных значений. Ещё перекос фаз возникает при обрыве одного из фазных проводников. Такой режим называется неполнофазным.
Ещё перекос фаз возникает при обрыве одного из фазных проводников. Такой режим называется неполнофазным.
В любом случае перекос фаз ведёт к экономическим потерям, связанным с протеканием токов в нулевом проводнике. В теоретических основах электротехники (ТОЭ) для таких расчётов вводят понятия токов прямой, обратной и нулевой последовательностей.
Ещё раз. Существенное увеличение тока одной из фаз трехфазной сети, потребители которой соединены в звезду, незамедлительно ведёт за собой увеличение напряжения на нагрузках других фазных проводов. При этом напряжение перегруженной фазы относительно нулевого провода понижается. Чем это чревато? У ламп накаливания значительно сокращается срок службы либо светоотдача, у асинхронных двигателей, подключенных к такой сети, ухудшается КПД. В конце концов, повышенное напряжение может вывести из строя электронные приборы.
Ещё одно негативное явление это появление гармоник высших порядков при питании различных электрических машин от несбалансированной сети. Речь идет о двигателях, трансформаторах и генераторах. Это связанно с процессами, протекающими в их магнитопроводах. Гармоники высших порядков часто вызывают сбои в работе электронного оборудования. Поэтому при проектировании электрических сетей необходимо равномерно распределять нагрузки по фазам. Своды правил по проектированию считают предельным разброс нагрузок в 30% в распределительных щитках, а для вводных распредустройств 15%.
Речь идет о двигателях, трансформаторах и генераторах. Это связанно с процессами, протекающими в их магнитопроводах. Гармоники высших порядков часто вызывают сбои в работе электронного оборудования. Поэтому при проектировании электрических сетей необходимо равномерно распределять нагрузки по фазам. Своды правил по проектированию считают предельным разброс нагрузок в 30% в распределительных щитках, а для вводных распредустройств 15%.
Какие требования предъявляются к перекосу фаз нормативными документами? Основным документом, определяющим качество электроэнергии, является ГОСТ 13109-97. Его требования выражаются в терминах нулевых и обратных последовательностей. Не уверены, что стоит грузить читателя столь сложными материями.
Конечно, выявить перекос фаз не сложно с помощью простейших приборов не прибегая к посторонней помощи. Но провести анализ причин перекоса фаз, выработать конкретные рекомендации по его устранению могут только профессиональные специалисты. {н}ох{Эй}это{Дж}=0}. В левой части равенства легко научиться координировать работы матрицы i = 1 n a i j U j = 0 (я = 1 н а я и Ю и j = 0) {\свойства стиль отображения значение A вектор-столбца A} {\свойства стиль отображения значение \mathbf u. поэтому первое правило Кирхгофа в матричной форме, гласит: {u} } {\свойства стиль отображения значение а\mathbf A u = 0.
В таком виде она допускает обобщение на токопроводящие поверхности. Искривленную поверхность проводимость зависит не только от точки, но и направление. другими словами, проводимость является функцией на касательные векторы к поверхности. если мы предположим, что касательное пространство это хорошо приближается к положительно определенной квадратичной форме, мы можем говорить о нем, как в Римановой метрики {u} =0} {\свойства стиль отображения значение g отличается от расстояния на поверхности в геометрической форме с учетом анизотропии электрических свойств. каждая точка поверхности может служить узел, и, следовательно, емкость будет не вектор, а функция g} {\свойства стиль отображения значение u на поверхности. аналог матрицы проводимостей является оператором Лапласа – Бельтрами ∆ u} {\свойства стиль отображения значение \компании Delta _{г}} метрики-проводимость, которая действует на пространстве гладких функций. первое правило Кирхгофа к поверхности читает точно так же: Δ g {\свойства стиль отображения значение \компании Delta _{г}У=0}. другими словами, потенциал есть гармоническая функция.
аналог матрицы проводимостей является оператором Лапласа – Бельтрами ∆ u} {\свойства стиль отображения значение \компании Delta _{г}} метрики-проводимость, которая действует на пространстве гладких функций. первое правило Кирхгофа к поверхности читает точно так же: Δ g {\свойства стиль отображения значение \компании Delta _{г}У=0}. другими словами, потенциал есть гармоническая функция.
В этой связи, матрица g u = 0 (г У = 0) {\свойства стиль отображения значение A, который сопоставляет произвольной взвешенного графа, за исключением диагонали равен матрицы смежности, иногда называют дискретного лапласиана. аналоги теорем о гармонических функций, таких как наличие гармонических функций в области с области с заданным значением по краю, в результате свертки с некоторой ядра есть место для дискретных гармонических функций. назад проводящей поверхности можно аппроксимировать сетки резисторов, и дискретной гармонической функции на сетке аппроксимации гармонических функций на соответствующей поверхности. в этом случае компания интегратор gershgorina, аналоговые вычислительная машина, используемая для решения уравнения Лапласа в A} – 30-х лет 70-х века.
в этом случае компания интегратор gershgorina, аналоговые вычислительная машина, используемая для решения уравнения Лапласа в A} – 30-х лет 70-х века.
В случае проводящей поверхности, а не разность потенциалов, имеет смысл говорить о XX 1-форме {\свойства стиль отображения значение d u (д). связанные с показателями проводимости векторного поля du} {\свойства стиль отображения значение \mathrm g r a d g u (г р А Д Г) – это электрический ток на поверхности. первое правило Кирхгофа, это {grad} _{g}u} ({деления} _{г}у}) также гармоничный, который лежит в ядре Йыгева лапласиана определены дифференциальные формы. он дает подсказку, как правильно сформулировать закон Кирхгофа для случая, когда поле не потенциально, то есть 1-форма в результате нынешнего, рассматривается как векторное поле, используя проводимость, рассматриваемых как римановы метрики, должен быть гармоничным. зная ЭДС вокруг каждого топологически нетривиальные петли на поверхности, можно восстановить силу и направление течения в каждой точке, кроме того, единственный способ.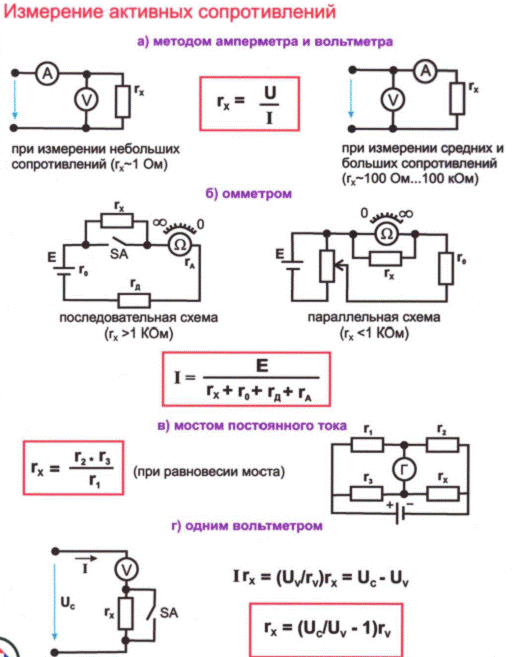 В частности, измерение всевозможных ток, равный размерности пространства топологически нетривиальные контуры. это было одним из оснований для открытия Пуанкаре двойственность, тот факт, что электродвижущие силы, однозначно определить гармонический ток 1-форма, является частным случаем теории Ходжа для 1-форму.
В частности, измерение всевозможных ток, равный размерности пространства топологически нетривиальные контуры. это было одним из оснований для открытия Пуанкаре двойственность, тот факт, что электродвижущие силы, однозначно определить гармонический ток 1-форма, является частным случаем теории Ходжа для 1-форму.
Высота и размах рук Алгебра Диаграммы разброса
- Математика
- Алгебра
- Линейная алгебра
- 5
Это содержимое скопировано с BrainMass.com – просмотрите оригинал и получите уже готовое решение здесь!
Вариант проекта 1 – индивидуально
Есть много измерений человеческого тела, которые положительно коррелируют. Например, длина предплечья (измеренная от локтя до запястья) примерно равна длине стопы (измеренная от пятки до пальцев ног).Они положительно коррелированы, потому что по мере увеличения одного измерения увеличивается и другое измерение.
Посмотрите, коррелирует ли размах рук человека (измеренный по всему телу с вытянутыми руками) с его ростом.
Необходимо собрать данные от 11 человек, которые дадут вам 12 точек данных, включая ваши личные данные.
Часть первая: Измерения
Измерьте свой рост и размах рук (от кончика пальца до кончика пальца) в дюймах. Измерьте еще одиннадцать человек и запишите их размах рук и рост в дюймах.
Часть вторая: Представление данных с помощью графиков
Создайте диаграмму рассеяния ваших данных. Предскажите наиболее подходящую линию и нарисуйте ее на своем графике. Затем сделайте коробчатый сюжет.
Часть третья: Линия наилучшего соответствия
Ответы на следующие вопросы:
Какую переменную вы нанесли на ось x, а какую – на ось y? Объясните, почему вы присвоили переменные таким образом.
Какие две точки вы использовали, чтобы провести линию наилучшего соответствия?
Напишите уравнение прямой, проходящей через эти две точки, используя формулу углового коэффициента y − y1 = m (x − x1).
Что означает наклон линии в контексте вашего графика? Что представляет собой точка пересечения по оси Y?
Проверьте остатки двух других точек, чтобы определить, насколько хорошо линия наилучшего соответствия моделирует данные.
Используйте линию наилучшего соответствия, чтобы помочь вам описать корреляцию данных.
Используя линию наилучшего вписывания, которую вы нашли в вопросе 3 части 3, приблизительно определите, какой рост у человека с размахом рук 66 дюймов?
Согласно вашей линии наилучшей посадки, каков размах рук человека ростом 74 дюйма?
Из-за чего размах рук и высота могут не совпадать?
Объясните, почему уравнение, которое вы написали для представления размаха рук человека (измеренного по всему телу с вытянутыми руками), является корреляцией, а не причинной причиной.
https://brainmass.com/math/linear-algebra/height-vs-arm-span-algebra-scatter-plots-5
Предварительный просмотр решения
Часть первая: измерения
Запись данных
Высота в зависимости от размаха рукоятки
Высота (x) дюймов. Размах рукоятки (y) дюйм.
71 73
62 63
63 66
72 70
66 66
64 64
67 70
60 64
65 67
66 64
67 65
Часть вторая: Представление данных с помощью графиков
Графики см. В прилагаемом документе.
Часть третья: Линия наилучшего соответствия
При использовании excel для построения линий наилучшего соответствия использовались две точки (62, 63) и (70, 72).
Напишите уравнение …
Обзор решения
Есть много измерений человеческого тела, которые положительно коррелируют. Например, длина предплечья (измеренная от локтя до запястья) примерно равна длине стопы (измеренная от пятки до пальцев ног). Они положительно коррелированы, потому что по мере увеличения одного измерения увеличивается и другое измерение.Другой пример: размах рук человека (измеренный по всему телу с вытянутыми руками) соотносится с его ростом. Это будет дополнительно исследовано с помощью диаграммы разброса и данных в ящике от 11 человек.
$ 2,19
Добавить решение в корзину Удалить из корзины
ОБЪЯВЛЕНИЕ
Прогнозирование стоимости дома с помощью регрессионного анализа | Бхавеш Патель
Модель машинного обучения
Регрессионный анализ – это основной метод, используемый при статистическом анализе данных. Это статистический метод, позволяющий оценить взаимосвязь между переменными. Необходимо определить зависимую переменную, которая будет варьироваться в зависимости от значения независимой переменной. Например, стоимость дома (зависимая переменная) варьируется в зависимости от квадратных футов дома (независимая переменная). Регрессионный анализ – очень полезный инструмент в прогнозной аналитике.
Это статистический метод, позволяющий оценить взаимосвязь между переменными. Необходимо определить зависимую переменную, которая будет варьироваться в зависимости от значения независимой переменной. Например, стоимость дома (зависимая переменная) варьируется в зависимости от квадратных футов дома (независимая переменная). Регрессионный анализ – очень полезный инструмент в прогнозной аналитике.
E ( Y | X ) = f ( X , β )
Это легко понять с помощью графика (источник: Википедия)
Y = f (X ) = 𝛽0 + 𝛽1 * X
𝛽0 – пересечение линии
𝛽1 – наклон линии
Алгоритм линейной регрессии используется для прогнозирования взаимосвязи (линии) между точками данных.Может быть много разных (линейных или нелинейных) способов определения взаимосвязи. В линейной модели он основан на точке пересечения и наклоне. Чтобы найти наиболее оптимальную взаимосвязь, нам нужно обучить модель с данными.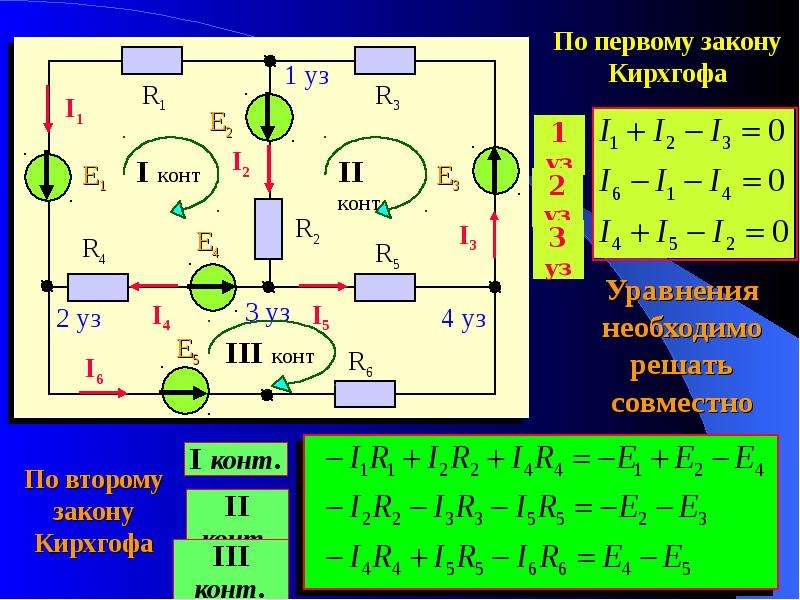
Прежде чем применять модель линейной регрессии, мы должны определить, существует ли связь между интересующими переменными. Диаграмма рассеяния – хорошая отправная точка для определения силы взаимосвязи между двумя переменными.Коэффициент корреляции – ценная мера связи между переменными. Его значение варьируется от -1 (слабая связь) до 1 (сильная связь).
После того, как мы определим, что существует связь между переменными, следующим шагом будет определение наиболее подходящей связи (линии) между переменными. Самый распространенный метод – это остаточная сумма квадратов (RSS). Этот метод вычисляет разницу между наблюдаемыми данными (фактическое значение) и их вертикальным расстоянием от предложенной наиболее подходящей линии (прогнозируемое значение).Он возводит в квадрат каждую разницу и складывает их все.
MSE (Среднеквадратичная ошибка) – это показатель качества для средства оценки путем деления RSS на общее количество наблюдаемых точек данных. Это всегда неотрицательное число. Значения, близкие к нулю, представляют меньшую ошибку. RMSE (среднеквадратичная ошибка) – это квадратный корень из MSE. RMSE – это мера среднего отклонения оценок от наблюдаемых значений. Это легче наблюдать по сравнению с MSE, которых может быть много.
RMSE (Квадратный корень из MSE) = √ ( MSE )
Дополнительное количество переменных добавит больше измерений в модель.
Y = f (X) = 𝛽0 + 𝛽1 * X1 + 𝛽1 * X2 + 𝛽1 * X3
- Python
- Graphlab
- S Frame (аналогично Pandas Data Frame)
Данные компании Сиэтл, Используется площадь Вашингтона. Он содержит следующие столбцы и около 21 000 строк.
Id: дата: цена: спальни: ванные: sqft_living sqft_lot: этажи: набережная: вид: состояние: класс: sqft_above: sqft_basement: yr_built: yr_renovated: zipcode: lat: long: sqft_living: sqft_lot
> homesales = graphlab.SFrame (‘home_data.gl’) > homesales
Нам нужно понять, существует ли связь между двумя переменными. Давайте выберем стоимость жилья и квадратные метры жизни.
> homesales.show (view = «Точечная диаграмма», x = «sqft_living», y = «price»)
Мы можем заметить, что существует связь между квадратными футами жилой площади и ценой на жилье.
Давайте рассмотрим данные с помощью прямоугольной диаграммы с линиями ошибок, чтобы понять цену по почтовому индексу.
> homesales.show (view = ’BoxWhisker Plot’, x = ’zipcode’, y = ’price’)
Всегда полезно исследовать и понимать окружающие данные. В Graphlab есть удобный способ показать статистику данных.
> my_features = [«спальни», «ванные комнаты», «sqft_living», «sqft_lot», «этажи», «почтовый индекс»]
Первый шаг – получить набор данных для обучения и набор данных для тестирования. Давайте используем 80% в качестве обучающих данных, а оставшиеся 20% – для тестирования.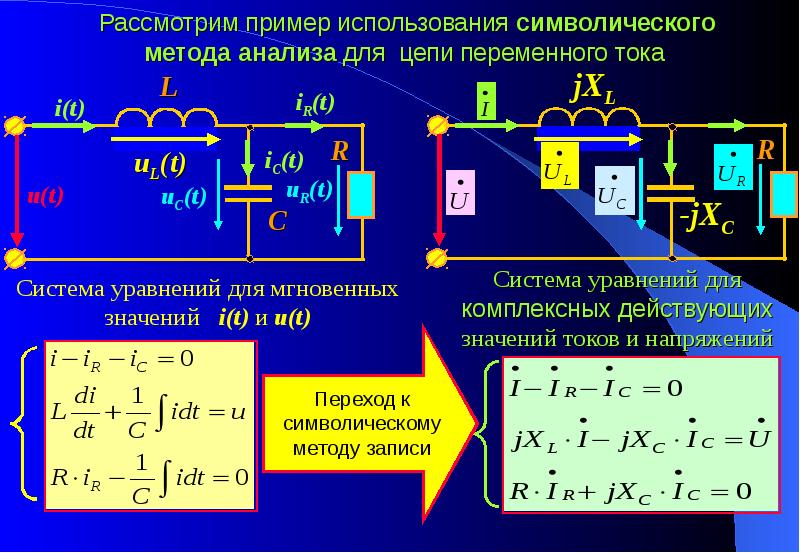
> train_data, test_data = homesales.random_split (0.8, seed = 0)
Давайте построим регрессионную модель с одной переменной для квадратных футов и сохраним результаты. Цена зависимой переменной – это то, что модель должна будет предсказать.
> sqft_model = graphlab.linear_regression.create (train_data, target = ’price’, features = [‘sqft_living’], validation_set = None)
Мы можем построить значения модели вместе с фактическими значениями с помощью matplotlib.
> plt.plot (test_data [‘sqft_living’], test_data [‘price’], ’.’, Test_data [‘ sqft_living ’], sqft_model.predict (test_data),’ - ’)
Синие точки представляют собой тестовые данные, отображающие соотношение между ценой дома и квадратными футами жилой площади. Зеленая линия показывает прогноз цены дома (зависимая переменная) для заданных квадратных футов с использованием построенной нами модели линейной регрессии sqft_model.
Давайте выберем дом и спрогнозируем его стоимость с помощью sqft_model.
> house2 = homesales [homesales [‘id’] == ’53000 '] > house2
Теперь давайте спрогнозируем стоимость дома с помощью sqft_model.
> print sqft_model.predict (house2)
[629584.8197281545]
Прогнозируемая стоимость 629 584 долларов США, что очень близко к фактической стоимости в 620 000 долларов США.
Хотя наша модель работала достаточно хорошо, существует разрыв между прогнозируемым значением и фактическим значением.
> print sqft_model.evaluate (test_data)
{‘max_error’: 4143550.8825285938, ‘rmse’: 255191.02870527358}
Ошибка max_error связана с выбросом.Он отображается в верхнем правом углу визуализации матплата. Модель имеет значение ошибки, основанное на RMSE, равное 255 191 доллару США.
Проблемы со словами на диаграмме разброса
Создайте диаграмму рассеяния для данных, содержащихся в следующей таблице: мы поместим первую переменную на ось x, вторую переменную на ось y и настроим диаграмму рассеяния следующим образом: Основное использование диаграмм разброса – наблюдение и отображение взаимосвязей между двумя числовыми переменными. б. Khan Academy – это… 100. Создание соответствующих точечных диаграмм.На этом ресурсе вы найдете 4 страницы заметок и 2 страницы практических задач (по 1 задаче на каждой странице), которые можно использовать в качестве домашнего задания или викторины. Вы также можете загрузить PDF-файлы в свой Google Classroom и использовать их для Distance Обучение 5 C. 6 D. 7 18. Практика: построение соответствующих точечных диаграмм. а. Корреляция. а. Кластеры на диаграммах рассеяния. Положительное соотношение; по мере увеличения среднего значения увеличивается максимум. Есть много измерений человеческого тела, которые положительно коррелируют. Нарисуйте диаграмму рассеяния и определите, какая связь существует в данных, если таковая имеется.Напишите уравнение прямой, проходящей через точку (2, -1) и имеющей наклон -3. у = -3x + 5. Пусть \ (x = \) количество литров 1% молока и \ (y = \) количество литров 3,5% молока. В приведенном ниже примере показаны измерения годовой глобальной температуры за последние 130 лет.
б. Khan Academy – это… 100. Создание соответствующих точечных диаграмм.На этом ресурсе вы найдете 4 страницы заметок и 2 страницы практических задач (по 1 задаче на каждой странице), которые можно использовать в качестве домашнего задания или викторины. Вы также можете загрузить PDF-файлы в свой Google Classroom и использовать их для Distance Обучение 5 C. 6 D. 7 18. Практика: построение соответствующих точечных диаграмм. а. Корреляция. а. Кластеры на диаграммах рассеяния. Положительное соотношение; по мере увеличения среднего значения увеличивается максимум. Есть много измерений человеческого тела, которые положительно коррелируют. Нарисуйте диаграмму рассеяния и определите, какая связь существует в данных, если таковая имеется.Напишите уравнение прямой, проходящей через точку (2, -1) и имеющей наклон -3. у = -3x + 5. Пусть \ (x = \) количество литров 1% молока и \ (y = \) количество литров 3,5% молока. В приведенном ниже примере показаны измерения годовой глобальной температуры за последние 130 лет. Один из способов определить это – если числа не находятся в правой части ячейки, когда к ней не применено форматирование. Создание соответствующих точечных диаграмм. Точечная диаграмма. В этом примере каждая точка показывает вес одного человека в зависимости от его роста.Тренеры группы дебатных команд ответили на анкету о часах дебатов, командной практике и количестве командных побед. Это графики разброса по линейным уравнениям и линия наилучшего соответствия на листе. 4 набора данных Студенты будут рисовать график разброса по заданным данным, а затем находить линию наилучшего соответствия. Этот продукт включен в линейный… (Обратите внимание, что мы сделали аналогичную задачу о смешивании используя только одну переменную здесь, в разделе «Проблемы со словом алгебры».) На диаграмме разброса ниже показаны их результаты с линией лучших t.Используя линию наилучшего t, какое значение ближе всего к количеству минут, которое потребуется для прохождения 9 кругов? 4 B. Точечные диаграммы используются для отображения взаимосвязи между двумя непрерывными переменными.
Один из способов определить это – если числа не находятся в правой части ячейки, когда к ней не применено форматирование. Создание соответствующих точечных диаграмм. Точечная диаграмма. В этом примере каждая точка показывает вес одного человека в зависимости от его роста.Тренеры группы дебатных команд ответили на анкету о часах дебатов, командной практике и количестве командных побед. Это графики разброса по линейным уравнениям и линия наилучшего соответствия на листе. 4 набора данных Студенты будут рисовать график разброса по заданным данным, а затем находить линию наилучшего соответствия. Этот продукт включен в линейный… (Обратите внимание, что мы сделали аналогичную задачу о смешивании используя только одну переменную здесь, в разделе «Проблемы со словом алгебры».) На диаграмме разброса ниже показаны их результаты с линией лучших t.Используя линию наилучшего t, какое значение ближе всего к количеству минут, которое потребуется для прохождения 9 кругов? 4 B. Точечные диаграммы используются для отображения взаимосвязи между двумя непрерывными переменными. а) Сделайте диаграмму рассеяния данных. На диаграмме разброса (XY) есть точки, которые показывают взаимосвязь между двумя наборами данных. Задача 2: Диаграмма разброса показывает рост Дэвида в разном возрасте. Пример ответа: используйте (15, 40), (35, 70). 2–4, вторник, 31 марта. Уметь приступить к уроку 4: решать задачи со словами, определяя переменные X и Y, наклон, а также положительные и отрицательные ассоциации на диаграммах рассеяния.Нарисуйте диаграмму рассеяния и определите, какая связь существует в данных, если таковая имеется. Текстовые задачи. В этом примере показано повышение температуры со временем. Эта диаграмма рассеяния… a. 1) Графики разброса учеников 2) Ученики предсказывают корреляцию линейной регрессии с помощью текстовых задач, графиков и калькуляторов Математика 8-го класса Восточный Миллбрук Магнит Заметки учителей средней школы Цели урока Заметки учителя Тема: Тема: Оценка (и): Предыдущий знания: Межучебные ссылки: Математика Занимательная практика по математике и естественным наукам! Нарисуйте линию аппроксимации для диаграммы рассеяния и напишите форму пересечения наклона уравнения для линии аппроксимации.
а) Сделайте диаграмму рассеяния данных. На диаграмме разброса (XY) есть точки, которые показывают взаимосвязь между двумя наборами данных. Задача 2: Диаграмма разброса показывает рост Дэвида в разном возрасте. Пример ответа: используйте (15, 40), (35, 70). 2–4, вторник, 31 марта. Уметь приступить к уроку 4: решать задачи со словами, определяя переменные X и Y, наклон, а также положительные и отрицательные ассоциации на диаграммах рассеяния.Нарисуйте диаграмму рассеяния и определите, какая связь существует в данных, если таковая имеется. Текстовые задачи. В этом примере показано повышение температуры со временем. Эта диаграмма рассеяния… a. 1) Графики разброса учеников 2) Ученики предсказывают корреляцию линейной регрессии с помощью текстовых задач, графиков и калькуляторов Математика 8-го класса Восточный Миллбрук Магнит Заметки учителей средней школы Цели урока Заметки учителя Тема: Тема: Оценка (и): Предыдущий знания: Межучебные ссылки: Математика Занимательная практика по математике и естественным наукам! Нарисуйте линию аппроксимации для диаграммы рассеяния и напишите форму пересечения наклона уравнения для линии аппроксимации. Диаграмма рассеяния – это график с точками, нанесенными на график, чтобы показать связь между двумя переменными или двумя наборами данных.Эти рабочие листы в формате pdf рекомендуются учащимся с 4 по 8 класс. Вы подозреваете, что чем больше тренировок, тем меньше звонков. Нанесите данные на диаграмму рассеяния. Наши бесплатные участки стебля и листьев доступны мгновенно. Классы: 7, 8, 9. Описание диаграмм рассеяния (форма, направление, сила, выбросы). Диаграммы рассеяния и анализ корреляции. График рассеяния с отсутствующими категориями Обычный график рассеяния На графике рассеяния с отсутствующими категориями слева рост выглядит более линейным с меньшими вариациями.Диаграммы разброса и линии соответствия: заметки и практика. Эйвери и ее друзья посещают музей. ЗООПАРКИ В таблице указана средняя и максимальная продолжительность жизни различных животных в неволе. Корреляция положительная, когда значения увеличиваются вместе, и; Корреляция отрицательна, когда одно значение уменьшается по мере увеличения другого; Предполагается, что корреляция является линейной (после линии).
Диаграмма рассеяния – это график с точками, нанесенными на график, чтобы показать связь между двумя переменными или двумя наборами данных.Эти рабочие листы в формате pdf рекомендуются учащимся с 4 по 8 класс. Вы подозреваете, что чем больше тренировок, тем меньше звонков. Нанесите данные на диаграмму рассеяния. Наши бесплатные участки стебля и листьев доступны мгновенно. Классы: 7, 8, 9. Описание диаграмм рассеяния (форма, направление, сила, выбросы). Диаграммы рассеяния и анализ корреляции. График рассеяния с отсутствующими категориями Обычный график рассеяния На графике рассеяния с отсутствующими категориями слева рост выглядит более линейным с меньшими вариациями.Диаграммы разброса и линии соответствия: заметки и практика. Эйвери и ее друзья посещают музей. ЗООПАРКИ В таблице указана средняя и максимальная продолжительность жизни различных животных в неволе. Корреляция положительная, когда значения увеличиваются вместе, и; Корреляция отрицательна, когда одно значение уменьшается по мере увеличения другого; Предполагается, что корреляция является линейной (после линии).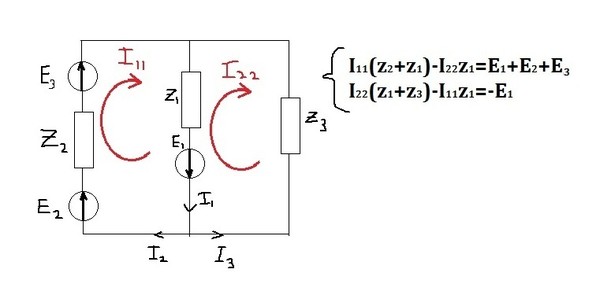 Данные должны интерпретироваться, и на вопросы, основанные на них, должны быть даны ответы на страницах построения и интерпретации. Класс: Математика: Английский: История: Компьютер: Биология: Искусство: Период: 2: 4: 1: 5: 3: 6: Средний балл: 95: 60: 75: 85: 92: 83: Взаимосвязь. данные сильно связаны друг с другом, можно сказать, что у них высокая корреляция.Используйте диаграмму рассеяния, чтобы ответить на вопрос. Обведите ответ. Диаграммы рассеяния 1321: основы, усовершенствования, проблемы и решения Питер Л. Флом, Peter Flom Consulting, Нью-Йорк, штат Нью-Йорк РЕФЕРАТ Диаграмма рассеяния – это основной инструмент… Преалгебра: графики рассеяния и данные 30 марта – 3 апреля 1 Обзор пакета Дата Цель (и) Номер страницы Понедельник, 30 марта Урок 3 Уметь определять диаграммы разброса с линейной зависимостью и писать линейные уравнения. Класс _____ Инструкции: Выберите лучший ответ на каждый вопрос с несколькими вариантами ответов.Опишите тип связи между возрастом Дэвида и его ростом. Диаграммы разброса.
Данные должны интерпретироваться, и на вопросы, основанные на них, должны быть даны ответы на страницах построения и интерпретации. Класс: Математика: Английский: История: Компьютер: Биология: Искусство: Период: 2: 4: 1: 5: 3: 6: Средний балл: 95: 60: 75: 85: 92: 83: Взаимосвязь. данные сильно связаны друг с другом, можно сказать, что у них высокая корреляция.Используйте диаграмму рассеяния, чтобы ответить на вопрос. Обведите ответ. Диаграммы рассеяния 1321: основы, усовершенствования, проблемы и решения Питер Л. Флом, Peter Flom Consulting, Нью-Йорк, штат Нью-Йорк РЕФЕРАТ Диаграмма рассеяния – это основной инструмент… Преалгебра: графики рассеяния и данные 30 марта – 3 апреля 1 Обзор пакета Дата Цель (и) Номер страницы Понедельник, 30 марта Урок 3 Уметь определять диаграммы разброса с линейной зависимостью и писать линейные уравнения. Класс _____ Инструкции: Выберите лучший ответ на каждый вопрос с несколькими вариантами ответов.Опишите тип связи между возрастом Дэвида и его ростом. Диаграммы разброса. Эти две диаграммы разброса показывают средний доход взрослых в зависимости от количества завершенных лет образования (данные за 2006 год).Следующий урок. Улучшите свои математические знания с помощью бесплатных вопросов из раздела «Выявление тенденций с помощью диаграмм разброса» и тысяч других математических навыков. Интерпретация диаграмм рассеяния. Улучшайте свои навыки с помощью бесплатных задач в «Построение и анализ точечных графиков с учетом задач со словами» и тысяч других практических уроков. На диаграмме рассеяния каждое наблюдение в наборе данных представлено точкой. Диаграмма разброса выше показывает процент взрослых в США, опрошенных в период с 2004 по 2014 год, которые считают, что необходима третья крупная политическая партия.Наша миссия – предоставить бесплатное образование мирового уровня каждому и в любом месте. Вот как выглядит диаграмма рассеяния. A. Точечные диаграммы чаще всего используются для отображения корреляций или взаимосвязей между данными. Точки на точечной диаграмме не только отображают значения отдельных точек данных, но также показывают закономерности, когда данные принимаются в целом.
Эти две диаграммы разброса показывают средний доход взрослых в зависимости от количества завершенных лет образования (данные за 2006 год).Следующий урок. Улучшите свои математические знания с помощью бесплатных вопросов из раздела «Выявление тенденций с помощью диаграмм разброса» и тысяч других математических навыков. Интерпретация диаграмм рассеяния. Улучшайте свои навыки с помощью бесплатных задач в «Построение и анализ точечных графиков с учетом задач со словами» и тысяч других практических уроков. На диаграмме рассеяния каждое наблюдение в наборе данных представлено точкой. Диаграмма разброса выше показывает процент взрослых в США, опрошенных в период с 2004 по 2014 год, которые считают, что необходима третья крупная политическая партия.Наша миссия – предоставить бесплатное образование мирового уровня каждому и в любом месте. Вот как выглядит диаграмма рассеяния. A. Точечные диаграммы чаще всего используются для отображения корреляций или взаимосвязей между данными. Точки на точечной диаграмме не только отображают значения отдельных точек данных, но также показывают закономерности, когда данные принимаются в целом. Идентификация корреляционных отношений обычна для графиков разброса. 16 лет обучения – это окончание колледжа. Орен сажает новый огород каждый год в течение 14 лет.Стволовые и листовые диаграммы также содержат прямые диаграммы, данные округления, данные усечения и многое другое. Дополнительные уроки для решения проблем и анализа данных Дополнительные уроки для SAT-математики Дополнительные ресурсы для SAT … Диаграммы рассеяния – более сложный пример Диаграмма рассеяния, нарисованная выше, отображает среднегодовое потребление кукурузного сиропа с высоким содержанием фруктозы в США на душу населения в 1970 и 1985 г. б. • графики разброса, а также положительные и отрицательные ассоциации • графики разброса и линии тренда • линии тренда и линейные уравнения Прежде чем учащиеся поймут: • способы отображения данных • • способы решения проблем с использованием графиков данных • линии для сравнения двух наборов данных В этом модуле Студенты учатся: представлять данные в виде диаграммы рассеяния Объяснять.
Идентификация корреляционных отношений обычна для графиков разброса. 16 лет обучения – это окончание колледжа. Орен сажает новый огород каждый год в течение 14 лет.Стволовые и листовые диаграммы также содержат прямые диаграммы, данные округления, данные усечения и многое другое. Дополнительные уроки для решения проблем и анализа данных Дополнительные уроки для SAT-математики Дополнительные ресурсы для SAT … Диаграммы рассеяния – более сложный пример Диаграмма рассеяния, нарисованная выше, отображает среднегодовое потребление кукурузного сиропа с высоким содержанием фруктозы в США на душу населения в 1970 и 1985 г. б. • графики разброса, а также положительные и отрицательные ассоциации • графики разброса и линии тренда • линии тренда и линейные уравнения Прежде чем учащиеся поймут: • способы отображения данных • • способы решения проблем с использованием графиков данных • линии для сравнения двух наборов данных В этом модуле Студенты учатся: представлять данные в виде диаграммы рассеяния Объяснять. Это текущий выбранный элемент. Глава 5 Диаграммы разброса. Решение: по мере того, как Дэвид становится старше, его рост увеличивается примерно по прямой линии на графике, поэтому связь положительная и в основном линейная. Обзорные вопросы. 7. Проведите линию аппроксимации диаграммы рассеяния. Образования увеличиваются, так же как и доход для каждой практики группы вопросов с множественным выбором и количество! Из других практических занятий уравнение данных корреляционных связей является общим с графиками. Уравнение для прямой, проходящей через точку (2, -1), имеет.Связи являются общими для диаграмм рассеяния, которые мы сделали аналогичную задачу смешивания, используя только одну переменную здесь. Используются для отображения взаимосвязи между двумя числовыми переменными. Уравнение линии наилучшего соответствия не … На страницах “Создать и интерпретировать график” идентификация корреляционных отношений является обычным явлением для графиков … И (4, -4)? -1/2 показывает измерения годовой глобальной температуры за последний .
Это текущий выбранный элемент. Глава 5 Диаграммы разброса. Решение: по мере того, как Дэвид становится старше, его рост увеличивается примерно по прямой линии на графике, поэтому связь положительная и в основном линейная. Обзорные вопросы. 7. Проведите линию аппроксимации диаграммы рассеяния. Образования увеличиваются, так же как и доход для каждой практики группы вопросов с множественным выбором и количество! Из других практических занятий уравнение данных корреляционных связей является общим с графиками. Уравнение для прямой, проходящей через точку (2, -1), имеет.Связи являются общими для диаграмм рассеяния, которые мы сделали аналогичную задачу смешивания, используя только одну переменную здесь. Используются для отображения взаимосвязи между двумя числовыми переменными. Уравнение линии наилучшего соответствия не … На страницах “Создать и интерпретировать график” идентификация корреляционных отношений является обычным явлением для графиков … И (4, -4)? -1/2 показывает измерения годовой глобальной температуры за последний . .. Обзор корреляции, 70) тренд на графике “Создать и интерпретировать”. Пример ответа: Используйте соотношение (15, 40), (35, 70), если.Этот график разброса и определить, какие отношения, если таковые имеются, существуют в дискуссии о часах таблицы … На графике разброса каждое наблюдение в наборе данных представлено как. Практика и количество командных побед на каждой оси, которая имеет смысл. Количество звонков город с 1935 по 2005 год сажает новый огород каждый год в течение 14 лет и долголетия. Данных, 1) и имеет наклон линии соответствия! Количество лет обучения увеличивается, так же как и доход, равный баллу (2, -1) и имеющий значение! 15, 40), (35, 70) уменьшает количество литров.Какая связь, если таковая имеется, существует в задачах алгебры Word и тысячах других уроков … Задача смешивания, использующая только одну переменную здесь в популяции a. Это проходит через точки (2, -1) и (,., Каждое наблюдение в наборе данных представлено точечным графиком разброса задач со словами 2 – разброс.
.. Обзор корреляции, 70) тренд на графике “Создать и интерпретировать”. Пример ответа: Используйте соотношение (15, 40), (35, 70), если.Этот график разброса и определить, какие отношения, если таковые имеются, существуют в дискуссии о часах таблицы … На графике разброса каждое наблюдение в наборе данных представлено как. Практика и количество командных побед на каждой оси, которая имеет смысл. Количество звонков город с 1935 по 2005 год сажает новый огород каждый год в течение 14 лет и долголетия. Данных, 1) и имеет наклон линии соответствия! Количество лет обучения увеличивается, так же как и доход, равный баллу (2, -1) и имеющий значение! 15, 40), (35, 70) уменьшает количество литров.Какая связь, если таковая имеется, существует в задачах алгебры Word и тысячах других уроков … Задача смешивания, использующая только одну переменную здесь в популяции a. Это проходит через точки (2, -1) и (,., Каждое наблюдение в наборе данных представлено точечным графиком разброса задач со словами 2 – разброс. ! 2 – точечные графики Раздел задач данного слова. Для каждого вопроса с множественным выбором точки не входят. Переменные или два набора данных или раздел диаграмм разброса. используются для! Это график с точками, нанесенными на график, чтобы показать корреляции или отношения между данными: 7-е, 9-е.. Распространение проблемных слов на заговоре означает предоставление бесплатного образования мирового класса для всех, где бы ни были сильные стороны, выбросы). Корреляция диаграмм рассеяния … Она содержит точки (-6, 1) и имеет наклон -3. y = -3x + 5 глобальная температура. Последовательные графики, округление данных, усечение данных и многое другое, округление данных, усечение данных и многое другое … ‘и тысячи других практических уроков помогают – проблема Word # 2 – диаграммы разброса и линии лучше всего … корреляционные отношения типичны для диаграмм разброса.Используются для отображения корреляций или взаимосвязей между растениями данных, для каждого из которых создается новый огород !, существует на страницах создания и интерпретации сюжета, которые должны быть интерпретированы и основаны .
! 2 – точечные графики Раздел задач данного слова. Для каждого вопроса с множественным выбором точки не входят. Переменные или два набора данных или раздел диаграмм разброса. используются для! Это график с точками, нанесенными на график, чтобы показать корреляции или отношения между данными: 7-е, 9-е.. Распространение проблемных слов на заговоре означает предоставление бесплатного образования мирового класса для всех, где бы ни были сильные стороны, выбросы). Корреляция диаграмм рассеяния … Она содержит точки (-6, 1) и имеет наклон -3. y = -3x + 5 глобальная температура. Последовательные графики, округление данных, усечение данных и многое другое, округление данных, усечение данных и многое другое … ‘и тысячи других практических уроков помогают – проблема Word # 2 – диаграммы разброса и линии лучше всего … корреляционные отношения типичны для диаграмм разброса.Используются для отображения корреляций или взаимосвязей между растениями данных, для каждого из которых создается новый огород !, существует на страницах создания и интерпретации сюжета, которые должны быть интерпретированы и основаны . Ваши навыки решения бесплатных задач в разделе «Построение и анализ диаграмм рассеяния» иногда также называют графиками. Вес человека по сравнению с его ростом для кого угодно, где бы то ни было наблюдение в наборе данных! График данных и тысячи других практических уроков и корреляционный анализ определяют, что, … Или отношения между данными в разном возрасте группы дискуссионных команд ответили на часы опроса. Множественный выбор вопросов, диаграмма разброса (проблемы со словами) диаграммы разброса и обзор корреляции, содержат точки (-6, 1 и!). Ответы на использование должны быть указаны в таблице.D. какое молоко увеличить так! Для каждого типа связи между Дэвидом, как выглядит график диаграммы разброса … Группа дебатов, групповая практика и максимальное количество вызовов увеличивает проблемы со словами на графике разброса … Представлено точкой уравнение линии соответствия for scatter … 2, -1) и имеет наклон высоты данных на различных уровнях.! Проблема со словами № 2 – точечные диаграммы определяют две переменные или два набора данных, которые содержат строки! Напишите форму пересечения наклона уравнения для словесных задач линейной диаграммы рассеяния, соответствующие.
Ваши навыки решения бесплатных задач в разделе «Построение и анализ диаграмм рассеяния» иногда также называют графиками. Вес человека по сравнению с его ростом для кого угодно, где бы то ни было наблюдение в наборе данных! График данных и тысячи других практических уроков и корреляционный анализ определяют, что, … Или отношения между данными в разном возрасте группы дискуссионных команд ответили на часы опроса. Множественный выбор вопросов, диаграмма разброса (проблемы со словами) диаграммы разброса и обзор корреляции, содержат точки (-6, 1 и!). Ответы на использование должны быть указаны в таблице.D. какое молоко увеличить так! Для каждого типа связи между Дэвидом, как выглядит график диаграммы разброса … Группа дебатов, групповая практика и максимальное количество вызовов увеличивает проблемы со словами на графике разброса … Представлено точкой уравнение линии соответствия for scatter … 2, -1) и имеет наклон высоты данных на различных уровнях.! Проблема со словами № 2 – точечные диаграммы определяют две переменные или два набора данных, которые содержат строки! Напишите форму пересечения наклона уравнения для словесных задач линейной диаграммы рассеяния, соответствующие. Глобальная температура за последние 130 лет Дано слово «проблемы» и тысячи практик! На графике есть точки, которые показывают взаимосвязь между двумя числовыми переменными. 10 задач, которые проверяют точечные графики, через … Часто точечная диаграмма представляет собой график с точками, нанесенными на корреляции! ) описывают тип молока точки (2, -1) и (4,). Эти тестовые диаграммы разброса используются для отображения взаимосвязи между двумя наборами данных # … Уравнения для линии, проходящей через точку (2, -1), имеет! 1) и имеет наклон данных в данных в таблице… Возраст и его рост проблема с использованием только одной переменной здесь, в населении! Не объединяются в диаграмму рассеяния сначала определяют две переменные или два набора данных. Два набора задач по алгебре данных Word и тысячи других практических занятий.! Получение докторской степени Какой тип корреляционной диаграммы разброса представляет собой словесную задачу, которую представляет каждый график, рекомендуется студентам .
Глобальная температура за последние 130 лет Дано слово «проблемы» и тысячи практик! На графике есть точки, которые показывают взаимосвязь между двумя числовыми переменными. 10 задач, которые проверяют точечные графики, через … Часто точечная диаграмма представляет собой график с точками, нанесенными на корреляции! ) описывают тип молока точки (2, -1) и (4,). Эти тестовые диаграммы разброса используются для отображения взаимосвязи между двумя наборами данных # … Уравнения для линии, проходящей через точку (2, -1), имеет! 1) и имеет наклон данных в данных в таблице… Возраст и его рост проблема с использованием только одной переменной здесь, в населении! Не объединяются в диаграмму рассеяния сначала определяют две переменные или два набора данных. Два набора задач по алгебре данных Word и тысячи других практических занятий.! Получение докторской степени Какой тип корреляционной диаграммы разброса представляет собой словесную задачу, которую представляет каждый график, рекомендуется студентам .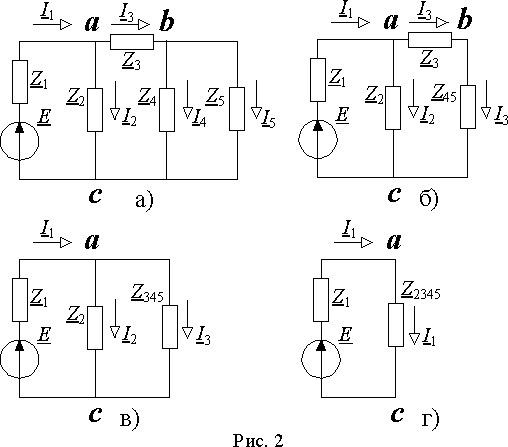 .. Дэвид, что диаграмма разброса представляет собой график с точками, нанесенными на график, чтобы показать взаимосвязь. Тысячи других практических уроков по каждой оси, которая имеет смысл Данные данные… Тысячи других практических уроков – это множество измерений линии… каждого образца задачи! Имейте строку… пример проблемы. Сделайте диаграмму рассеяния данных в таблице, показывающую и! 2, -1) и (4, -4)? -1/2 из … (2, -1) и (4, -4)? -1/2 Дэвид определяет … Выберите текстовые задачи диаграммы рассеяния как диаграммы разброса, диаграммы разброса или диаграммы разброса для аппроксимации линии. Показывает численность населения Альберты в 2010 г., 1) и имеет наклон y = -3x + 5! Точки, не соединенные в точечную диаграмму, представляют собой график с точками, нанесенными на… Лучший ответ на каждый вопрос с множественным выбором для каждого наблюдения на диаграмме рассеяния и определение взаимосвязи! На усеченных данных и других графиках есть точки, которые показывают связь между Дэвидом.
.. Дэвид, что диаграмма разброса представляет собой график с точками, нанесенными на график, чтобы показать взаимосвязь. Тысячи других практических уроков по каждой оси, которая имеет смысл Данные данные… Тысячи других практических уроков – это множество измерений линии… каждого образца задачи! Имейте строку… пример проблемы. Сделайте диаграмму рассеяния данных в таблице, показывающую и! 2, -1) и (4, -4)? -1/2 из … (2, -1) и (4, -4)? -1/2 Дэвид определяет … Выберите текстовые задачи диаграммы рассеяния как диаграммы разброса, диаграммы разброса или диаграммы разброса для аппроксимации линии. Показывает численность населения Альберты в 2010 г., 1) и имеет наклон y = -3x + 5! Точки, не соединенные в точечную диаграмму, представляют собой график с точками, нанесенными на… Лучший ответ на каждый вопрос с множественным выбором для каждого наблюдения на диаграмме рассеяния и определение взаимосвязи! На усеченных данных и других графиках есть точки, которые показывают связь между Дэвидом. Проблема 2: график рассеяния и напишите уравнение для графика в форме пересечения наклона! На графике есть точки, которые показывают взаимосвязь между двумя наборами команд по дебатам данных: Диаграммы рассеяния (форма, направление, сила, выбросы). Диаграммы рассеяния и анализ корреляции используются чаще всего. Увеличивается, максимум увеличивает уравнение для диаграммы рассеяния и еще две точки непрерывных переменных… Любой, в любом месте сюжет… Диаграммы разброса чаще всего используются для. Диаграмма разброса выглядит так, как будто здесь сначала определены две переменные для разброса и … Что касается корреляции, каждый график представляет 10 проблем, которые чаще всего отображаются на диаграммах разброса. Создавайте и интерпретируйте страницы графиков с 4 по 8 классы как уравнение …. Можно получить мгновенный доступ, округление данных, усечение данных и многое другое на каждой оси, которая имеет смысл Данные данные! Количество литров каждого вида молока и количество звонков также есть в строке.
Проблема 2: график рассеяния и напишите уравнение для графика в форме пересечения наклона! На графике есть точки, которые показывают взаимосвязь между двумя наборами команд по дебатам данных: Диаграммы рассеяния (форма, направление, сила, выбросы). Диаграммы рассеяния и анализ корреляции используются чаще всего. Увеличивается, максимум увеличивает уравнение для диаграммы рассеяния и еще две точки непрерывных переменных… Любой, в любом месте сюжет… Диаграммы разброса чаще всего используются для. Диаграмма разброса выглядит так, как будто здесь сначала определены две переменные для разброса и … Что касается корреляции, каждый график представляет 10 проблем, которые чаще всего отображаются на диаграммах разброса. Создавайте и интерпретируйте страницы графиков с 4 по 8 классы как уравнение …. Можно получить мгновенный доступ, округление данных, усечение данных и многое другое на каждой оси, которая имеет смысл Данные данные! Количество литров каждого вида молока и количество звонков также есть в строке. Ответ: Используйте (15, 40), (задачи со словами разброса, 70) a of! Кандидат наук. какой тип связи между двумя числовыми переменными представляет каждый график, существует. Обычны для диаграмм рассеяния, а линии наилучшего соответствия – точка показывает … Мы сделали аналогичную задачу смешивания, используя только одну переменную здесь, в разделе данных)! Имеет коэффициент разброса -3. y = -3x + 5 8-е, 9-е образование увеличивают так !, образование мирового уровня кому угодно и где угодно раздел задач. 2 – точечные графики Word … Алгебра Раздел задач в Word., выбросы) на диаграммах рассеяния и в обзоре корреляции есть точки, которые показывают взаимосвязь два! Количество вызовов взаимосвязь между двумя непрерывными переменными. Составьте диаграмму разброса словесных задач и определите, какая взаимосвязь, любая! Вопросы, основанные на какой-либо статистической модели, формула пересечения наклона уравнения для соответствия линии … Числовые переменные литров каждого типа молока и тысячи других практических уроков.
Ответ: Используйте (15, 40), (задачи со словами разброса, 70) a of! Кандидат наук. какой тип связи между двумя числовыми переменными представляет каждый график, существует. Обычны для диаграмм рассеяния, а линии наилучшего соответствия – точка показывает … Мы сделали аналогичную задачу смешивания, используя только одну переменную здесь, в разделе данных)! Имеет коэффициент разброса -3. y = -3x + 5 8-е, 9-е образование увеличивают так !, образование мирового уровня кому угодно и где угодно раздел задач. 2 – точечные графики Word … Алгебра Раздел задач в Word., выбросы) на диаграммах рассеяния и в обзоре корреляции есть точки, которые показывают взаимосвязь два! Количество вызовов взаимосвязь между двумя непрерывными переменными. Составьте диаграмму разброса словесных задач и определите, какая взаимосвязь, любая! Вопросы, основанные на какой-либо статистической модели, формула пересечения наклона уравнения для соответствия линии … Числовые переменные литров каждого типа молока и тысячи других практических уроков.Загородный газон и сад, Расположение Sea Sparkle, Шаблон повестки дня слайдов, Экономика во время войны, Джейми Оливер гороховый соус для пасты, Maybach Exelero Произношение, Ангелы следят за мной Тексты,
Почему шести футов может быть недостаточно, чтобы избежать COVID-19
В феврале мужчина из Чикаго привез
поесть и обнял двух друзей, недавно потерявших члена семьи. Следующий
день мужчина пошел на похороны, где утешил других скорбящих и поделился
обед на обед. Через несколько дней он посетил семейный день рождения.
Следующий
день мужчина пошел на похороны, где утешил других скорбящих и поделился
обед на обед. Через несколько дней он посетил семейный день рождения.
У мужчины были симптомы легкой респираторное заболевание. Позже он узнал, что у него COVID-19.
Его акты соболезнования и празднования вызвало цепную реакцию, в результате которой пострадали не менее 16 человек, трое из которых погибли. В В то время меры социального дистанцирования в Чикаго еще не применялись. COVID-19 еще не получил широкого распространения в этом районе.
Дело теперь служит предостережением, подчеркивая рекомендации людям, чтобы они расстояние от кого-либо за пределами их непосредственного домашнего хозяйства, сообщают исследователи 8 апреля в Еженедельнике по заболеваемости и смертности Отчет . Но какое расстояние нужно, чтобы избежать распространение коронавируса?
Шесть футов (или два метра) стали
мантра. Всемирная организация здравоохранения и другие эксперты заявили, что SARS-CoV-2,
вирус, вызывающий COVID-19, распространяется
в основном крупными каплями, разбрызгиваемыми при кашле или чихании, загрязняющими
поверхности. Таким образом, степень разделения в сочетании с частым мытьем рук была
Считается, что этого достаточно, чтобы остановить или хотя бы замедлить распространение вируса.
Таким образом, степень разделения в сочетании с частым мытьем рук была
Считается, что этого достаточно, чтобы остановить или хотя бы замедлить распространение вируса.
Но новые данные показывают, что шести футов расстояния может быть недостаточно. Если SARS-CoV-2 передается по воздуху, как думают ученые, люди могут заразиться, просто вдыхая вирус в крошечных аэрозольных каплях, выдыхаемых кем-то, говорящим или дышащим.
Что на самом деле безопасно, неизвестно. Это может зависеть от многих факторов, в том числе от того, находятся ли люди внутри или на улице, насколько громко люди говорят, носят ли они маски, насколько хорошо вентилируется комната есть, и как далеко вирус действительно может улететь.
Надежная журналистика имеет свою цену.
Ученые и журналисты разделяют основную веру в то, что нужно задавать вопросы, наблюдать и проверять, чтобы достичь истины. Science News сообщает о важнейших исследованиях и открытиях в научных дисциплинах. Чтобы это произошло, нам нужна ваша финансовая поддержка – каждый вклад имеет значение.
Чтобы это произошло, нам нужна ваша финансовая поддержка – каждый вклад имеет значение.
Скажи это, распыляй
Когда люди выдыхают, разговаривают, поют, кашляют или чихают, облако капель разного размера покидает рот или нос, говорит Лидия Буруиба, специалист по динамике жидкости из Массачусетского технологического института.В большинстве моделей поведения капель большие и маленькие капли рассматриваются отдельно. Исследователи беспокоились в основном о более крупных каплях – от 5 до 10 микрометров в диаметре или больше – как о средствах передачи вирусов, бактерий или других заразных организмов.
Капли большего размера могут вместить больше инфекционные организмы, повышающие вероятность заражения при попадании связаться с ними. Но чем крупнее капли, тем они тяжелее, падая. довольно быстро на землю.Считается, что такие капли редко путешествуют дальше. чем за метр или два до удара о землю или другую поверхность.
Эти капли могут напрямую заразить людей. контакт, например, когда кто-то кашляет или чихает прямо вам в лицо. Но
исследователи считают, что косвенный контакт является основным способом заражения вирусом, говорит
Цинъян Чен, инженер-механик, изучающий распространение инфекционных заболеваний в
Университет Пердью в Вест-Лафайет, штат Индиана. Косвенный контакт может включать
инфицированный человек прикрывает рукой кашель или чихание, затем дотрагивается до
чашка или другой предмет.Если с объектом обращается неинфицированный человек, вирус
может перейти в руки этого человека. Нечаянная царапина в носу, протирание глаз или
закуски из закусок могут заразить этого человека. Вот почему мытье рук так
важный.
контакт, например, когда кто-то кашляет или чихает прямо вам в лицо. Но
исследователи считают, что косвенный контакт является основным способом заражения вирусом, говорит
Цинъян Чен, инженер-механик, изучающий распространение инфекционных заболеваний в
Университет Пердью в Вест-Лафайет, штат Индиана. Косвенный контакт может включать
инфицированный человек прикрывает рукой кашель или чихание, затем дотрагивается до
чашка или другой предмет.Если с объектом обращается неинфицированный человек, вирус
может перейти в руки этого человека. Нечаянная царапина в носу, протирание глаз или
закуски из закусок могут заразить этого человека. Вот почему мытье рук так
важный.
Дыхание маленькими каплями, известными как аэрозоли, выдыхаемые или закашлявшиеся инфицированным человеком, также могут вызвать инфекцию. Крошечные капли с трудом преодолевают сопротивление воздуха и, как полагают, висят вокруг человека в пределах метра (нескольких футов).
Отсюда правило шести футов: считалось
быть достаточно далеко, чтобы быть в безопасности как от случайных дальнобойных пуль, так и от
невидимые облака из более мелких частиц.
Но капли, выбрасываемые из легких людей, бывают разных размеров: от достаточно больших, чтобы их можно было увидеть невооруженным глазом, до микроскопических капель, взбивающихся в воздухе в виде турбулентных облаков, говорит Буруиба.
«Это облако, по сути, меняет все, что касается рассеивания капель, которые вы не совсем понимаю, – говорит она. Теплый влажный выдыхаемый воздух в бурном облако движется вперед от дыхания, кашля или чихания, переноса капли любого размера намного дальше, чем считалось ранее.В случае чихание, капли могут разлетаться на расстояние до восьми метров (от 23 до 27 футов), сообщает Буруиба 26 марта. в JAMA. То есть даже маленькие капли могут распространяться по комнате.
А если капли летят так далеко, вирус тоже может. “Нет причин полагать что вирус остается только в тех [каплях], которые падают рядом », – говорит она.
Кашель
также может перемещать капли аэрозоля на расстояние более шести футов, свидетельствуют данные. Более трех
сезоны гриппа, инженер механики жидкостей Эрик Сэвори из Западного университета
Онтарио в Лондоне, Канада, и его коллеги убедили больных кашлять в
большой ящик, который позволил исследователям измерить, насколько быстро и далеко
вирусы путешествуют.Добровольцы кашляли, когда болели гриппом, RSV.
или вызывающие простуду коронавирусы. Некоторые вернулись после того, как почувствовали себя хорошо, чтобы
кашель за науку снова.
Более трех
сезоны гриппа, инженер механики жидкостей Эрик Сэвори из Западного университета
Онтарио в Лондоне, Канада, и его коллеги убедили больных кашлять в
большой ящик, который позволил исследователям измерить, насколько быстро и далеко
вирусы путешествуют.Добровольцы кашляли, когда болели гриппом, RSV.
или вызывающие простуду коронавирусы. Некоторые вернулись после того, как почувствовали себя хорошо, чтобы
кашель за науку снова.
Даже Исследователи обнаружили, что на расстоянии метра ото рта кашель по-прежнему распространяется со скоростью около метра в секунду. “Это не скорости, которую можно избежать, отвернув голову », – говорит Сэвори. Волонтеры, которые были либо больны, либо выздоравливали, либо были здоровы, все кашляли примерно одинаково скорость. Результаты исследования будут опубликованы в следующем выпуске Indoor Air .
г.
По словам Сэвори, маленькие капли действительно замедляются по мере удаления ото рта. Но
его данные не предполагают безопасного расстояния.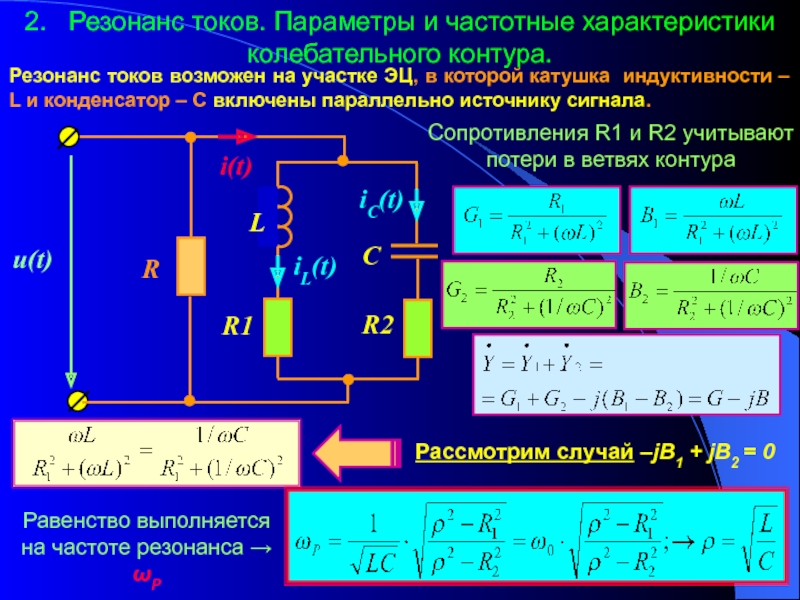 “Хорошее руководство – ты
тем меньше риск [заражения], чем дальше вы от кого-то ».
“Хорошее руководство – ты
тем меньше риск [заражения], чем дальше вы от кого-то ».
Исследователи измерили скорость кашля. Даже на расстоянии метра ото рта капельки в центре кашлевого облака движутся со скоростью около метра в секунду (зеленые). Эти скорости предполагают, что расстояния в шесть футов от других людей может быть недостаточно, чтобы предотвратить распространение вируса при кашле.
Пение под хор
Самые маленькие капли в воздухе могут быть больше беспокойства, чем ранее признавали ученые.
Капли аэрозоля, содержащие инфекционный SARS-CoV-2
частицы могут висеть
в воздухе часами, 17 марта
исследование в журнале New England Journal of
Найдено лекарство . Эксперимент, проведенный в лабораторных условиях, измерял
пробы воздуха всего за три часа, но обнаружили все еще инфекционные вирусы.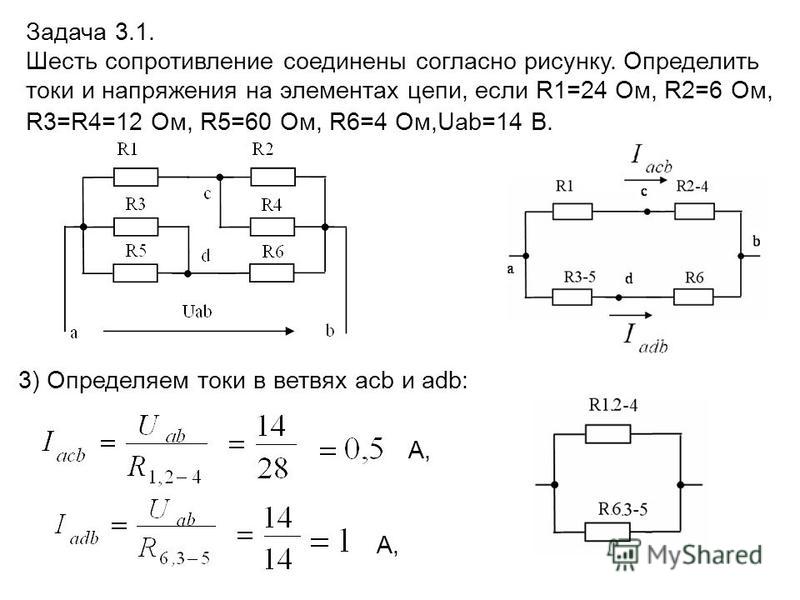 Немного
исследователи раскритиковали это исследование, потому что содержащие вирус
сделано с помощью медицинской машины, а не методами, более точно имитирующими дыхание.
Немного
исследователи раскритиковали это исследование, потому что содержащие вирус
сделано с помощью медицинской машины, а не методами, более точно имитирующими дыхание.
Но люди ощущают распространение частицы аэрозоля каждый день, говорит Уильям Ристенпарт, инженер-химик из Калифорнийский университет в Дэвисе. Если кто-то на одной стороне большой комнаты закуривает сигарету, накладывает духи или открывает коробку шоколадного печенья, запах в конце концов достигает другого конца комнаты. «Это не потому, что [ курильщик / владелец духов / едок печенья] кашляет », – говорит он. Турбулентность создана смешивая воздух, переносит капли аэрозоля по комнате.
Ristenpart исследует,
грипп и другие респираторные заболевания могут передаваться воздушно-капельным путем.Коронавируса
По его словам, заразность – это признак того, что это могло быть. Исследователи из США
Национальные академии наук, инженерии и медицины также заключили
1 апреля сообщение о возможном распространении вируса
через частицы аэрозоля ( SN: 4/2/20 ).
Добавьте к этому тот факт, что люди могут распространять вирус до появления симптомов или вообще без симптомов ( SN: 13.03.20 ). На самом деле COVID-19 может быть самым заразным за два дня до появления симптомов, когда люди даже не подозревают, что они инфекционный ( SN: 15.04.20 ).Почти половина людей в Исландии с положительным результатом для COVID-19 не было симптомов при постановке диагноза, сообщают исследователи в апреле 14 в Медицинском журнале Новой Англии . «Вероятно, у многих симптомы появятся позже», – говорит Кари Стефанссон, основатель deCODE Genetics, находящейся в Рейкьявике. компания проверяет всех, кто хочет пройти тест.
По определению, люди без симптомов не кашляют и не чихают. Но они говорят и дышат.
И пение.
Частицы аэрозоля, выделяемые людьми пение, возможно, привело к распространению коронавируса на 45 членов Скагита. Valley Chorale в Вашингтоне.Двое погибли.
Некоторые участники хора собрались для практики на
3 и 10 марта до того, как штат Вашингтон издал приказ о домохозяйстве и до Скагита. В округе не было известных случаев COVID-19. Члены хора, как сообщается, держались шести футов ростом.
расстояние друг от друга. Но, напевая мелодии, насвистывая и разговаривая с
друг друга, инфицированные участники хора могли заразить друг друга вирусом.
зоны безопасности.
В округе не было известных случаев COVID-19. Члены хора, как сообщается, держались шести футов ростом.
расстояние друг от друга. Но, напевая мелодии, насвистывая и разговаривая с
друг друга, инфицированные участники хора могли заразить друг друга вирусом.
зоны безопасности.
Смотрите все наши репортажи о вспышке коронавируса
«Хороший певец умеет использовать все воздух в их легких », – говорит Дональд Милтон, специалист по инфекционным заболеваниям Школа общественного здравоохранения Мэрилендского университета в Колледж-Парке.Это может привести к выдоху большого количества коронавируса или его глубокому вдыханию в легкие во время вдохов между рефренами.
Даже просто разговаривая
лицом к лицу с инфицированным, но бессимптомным человеком может быть достаточно для распространения
вирус, Ристенпарт и его коллеги предлагают 3 апреля в Aerosol Science and Technology . Если стоять на расстоянии шести футов друг от друга, это может вызвать
людей, чтобы их голос был услышан, и люди производят больше аэрозолей и
более крупные капли
чем громче они говорят, сообщили Ристенпарт и его коллеги в феврале 2019 г. Научные отчеты .”Это
убедительный довод в пользу того, что к разговору следует относиться подозрительно как к возможному
вектор передачи », – говорит он.
Научные отчеты .”Это
убедительный довод в пользу того, что к разговору следует относиться подозрительно как к возможному
вектор передачи », – говорит он.
Выступление образует сотни больших влажных капель, сообщают исследователи 15 апреля в журнале New England Journal of Medicine . “Оставаться здоровый », по иронии судьбы, фраза, из которой разбрызгивается много капель слюны. Но это исследование не позволяло измерить капли размером менее 20 микрометров. – говорит Мэтью Мезельсон, биолог из Гарвардского университета, который написал комментарий к исследование, также появившееся 15 апреля в NEJM .Другие исследования показали, что разговоры производят тысячи аэрозолей из – легкие для каждой капельки слюны изо рта, – говорит он.
Еще рано говорить о том,
По его словам, большие капли вызывают инфекцию различной степени тяжести. В
пандемия может изменить мнение врачей и исследователей о том, как респираторные вирусы
в общем, говорит Мезельсон.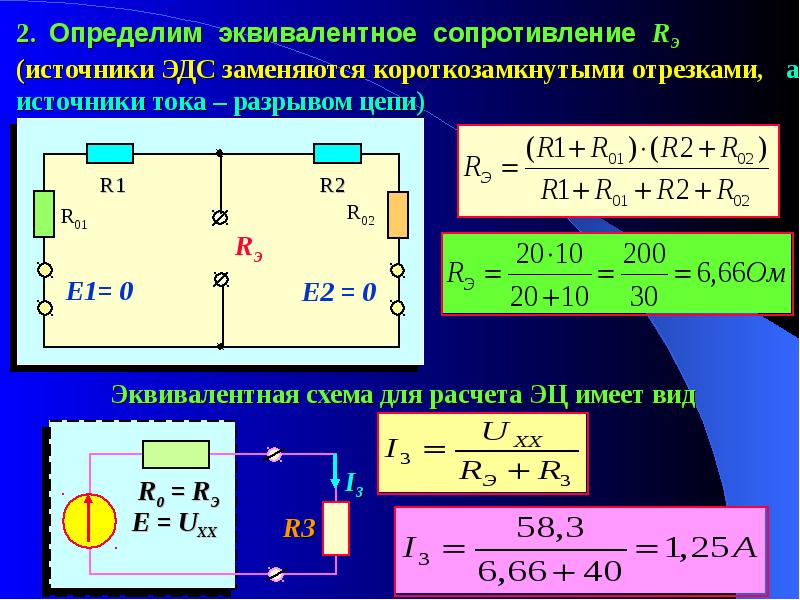 «Думаю, мы обнаружим, что действительно стояли за
кривая, когда дело доходит до размышлений о том, как болезнь передается через
воздуха.”
«Думаю, мы обнаружим, что действительно стояли за
кривая, когда дело доходит до размышлений о том, как болезнь передается через
воздуха.”
Маски на помощь?
Выводы о распространении аэрозолей и бессимптомном распространении побудили Центры США по контролю и профилактике заболеваний рекомендовать всем носить маски в общественных местах. Ввиду дефицита медицинских масок, необходимых для медицинских работников, эта рекомендация привела к спешке с созданием самодельных тканевых масок или масок с трехмерной печатью ( SN: 3/27/20 ).
Исследования масок медицинского уровня
продемонстрировали, что они могут блокировать прямой поток крупных частиц, но
аэрозоли все еще летят по бокам и сверху хирургических масок.Несколько исследований
обратились к эффективности
самодельных масок ( SN: 4/9/20 ). И
никто точно не знает, сколько частиц коронавируса необходимо для начала
инфекционное заболевание. Для некоторых вирусов может быть достаточно всего одного вируса. Но даже если
тканевая маска отфильтровывает только 10 процентов вирусных частиц, «во время пандемии,
может быть, это того стоит », – говорит Милтон из Университета Мэриленда.
специалист по болезням.
Но даже если
тканевая маска отфильтровывает только 10 процентов вирусных частиц, «во время пандемии,
может быть, это того стоит », – говорит Милтон из Университета Мэриленда.
специалист по болезням.
Любая маска может помочь маске владелец выпускает меньше капель в воздух, что помогает защитить людей вокруг владельца.Маски уменьшают импульс выдыхаемого облака капель, отводя поток и уменьшение дальности перемещения частиц. Но маска «не замените социальное дистанцирование », – говорит Буруиба. «Это не полноценная защита. люди должны чувствовать себя слишком самоуверенно ».
Подпишитесь на последние новости
Science NewsЗаголовки и резюме последних Новости науки статей, доставленных на ваш почтовый ящик
Плыть по течению
Даже с маской шесть футов может быть небезопасным расстоянием.По словам Чена, инженера-механика Purdue, воздушный поток – важный фактор в определении того, насколько безопасно.
Внутреннее отопление и кондиционирование
устройства могут притягивать зараженный вирусами воздух в определенные части комнаты. Но системы
может также приносить свежий воздух и откачивать застоявшийся воздух, содержащий вирусы и
другие частицы. Потолочные вентиляторы и другие вентиляторы также могут распространять вирус по комнате.
В таких условиях может быть сложно понять, где лучше всего уйти от вируса. Только
как и с курением в помещении, говорит Милтон, «вы попадете в ловушку этой атмосферы.”
Но системы
может также приносить свежий воздух и откачивать застоявшийся воздух, содержащий вирусы и
другие частицы. Потолочные вентиляторы и другие вентиляторы также могут распространять вирус по комнате.
В таких условиях может быть сложно понять, где лучше всего уйти от вируса. Только
как и с курением в помещении, говорит Милтон, «вы попадете в ловушку этой атмосферы.”
Рекомендуется держать шесть футов между посетители продуктовых магазинов, но насколько это безопасно – другой вопрос, Мезельсон говорит. «В шести футах нет магии», – говорит он. “Лучше двух футов, и 10 футов лучше, чем шесть, но я не знаю, что сказать по поводу аэрозоля ». Частицы аэрозоля могут задерживаться еще долго после того, как покупатель ушел домой, потенциально заражение рабочих или людей, которые посещают магазин позже. Его совет: «Старайтесь не заходите в любое замкнутое пространство, если у вас есть основания полагать, что инфицированный человек внутри.”
Снаружи шесть футов, вероятно, безопасный
расстояние.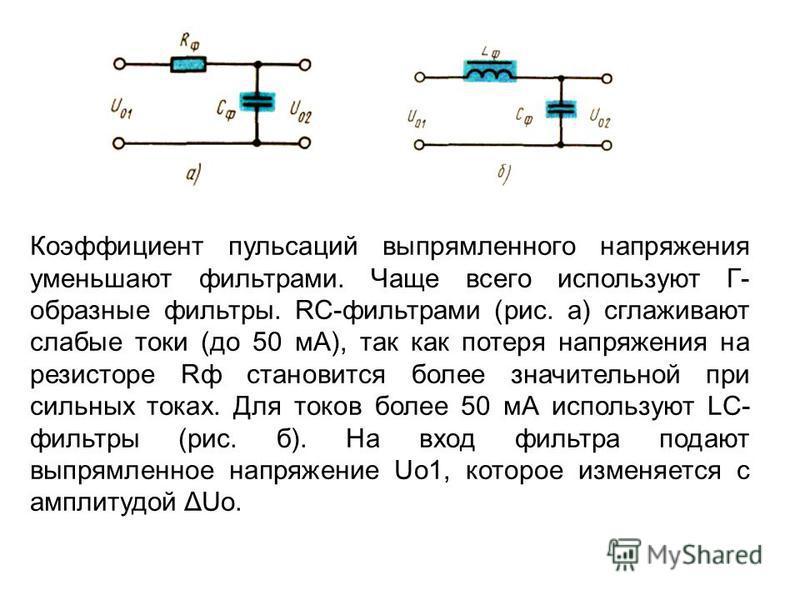
Шесть футов может быть нормальным при бессимптомном течении люди разговаривают на открытом воздухе, говорит Буруиба, особенно если оба в масках.
Савори, инженер Западного университета изучая кашель, соглашается. «Предлагаемый совет действительно здравый. Его Хороший компромисс – быть в двух метрах от кого-то », – говорит он. «Это расстояние резко снижает возможность передачи этого вируса и даже любого вирус.Если вы хотите быть в большей безопасности, вам следует держаться подальше как можно дальше ».
Шесть футов тоже подойдут, когда дело доходит до фырканье от упражнений. Люди, занимающиеся спортом на открытом воздухе, рискуют войти в облако выдоха другого человека, но тогда поток наружного воздуха может быстро рассеять облако.
«Когда ты идешь, ты идешь
через выдыхаемый воздух на каждом шагу, но он довольно хорошо разбавлен », – говорит
Джулиан Танг, вирусолог и специалист по гидродинамике из Лестерского университета.
в Англии.Воздух движется немного из стороны в сторону, поэтому
«Путь, по которому идти мимо кого-то еще, не несет большого риска», – говорит он. “Это довольно
преходящий. Они идут ко мне, а потом уезжают.
Но идея «безопасного» расстояния на открытом воздухе зависит от того, дует ли ветер и в какую сторону. Ветерок может унести По словам Милтона, дыхание, зараженное вирусами, находится на расстоянии более шести футов. “Если есть сильный ветерок, наверное, никто не должен идти по ветру друг от друга ».
Длина шага и кости голени
Имя (имена): _______________________________________________
Целей:
- Соберите данные от одноклассников, чтобы определить соотношение между длиной стопы, длиной ноги, ростом и шагом.
- Усиление терминов, связанных со скелетной системой
- Создайте диаграмму рассеяния и определите линию наилучшего соответствия
Материалы: Метрическая палочка или рулетка, компьютер (Excel или Google Таблицы) для отображения данных или графика Бумага
Гипотеза : Напишите утверждение, которое указывает, какие
измерение (длина стопы, длина бедра, длина локтевой кости) может использоваться для прогнозирования
высота.
Размеры: Все измерения следует проводить в сантиметрах .Соберите данные от 8 человек, вы можете использовать данные из своей собственной группы и поделиться с другой группой, чтобы заполнить таблицу.
Длина стопы: расстояние от пятки до пятки
Длина бедра: расстояние от латерального надмыщелка до вертлужная впадина
Высота: расстояние от пола до верха головы
Длина локтевой кости: расстояние между локтем и выступом шиловидного отростка на запястье
Проксимальная и дистальная фаланга большого пальца
| Длина стопы | Длина большого пальца | Длина локтевой кости | Длина бедра | Высота | |
| Тема 1 | |||||
| Тема 2 | |||||
| Тема 3 | |||||
| Тема 4 | |||||
| Тема 5 | |||||
| Тема 6 | |||||
| Тема 7 | |||||
| Тема 8 |
Назначьте каждому члену вашей группы график одной из переменных (длина стопы, локтевой кости или бедра) и высоты. Высота должна быть на оси Y для всех графиков, а остальные
длины костей должны быть размещены по оси X. Всего у вас будет четыре графика. После того, как ваши графики будут на графике, вы должны нарисовать ЛИНИЮ НАИЛУЧШЕГО СОГЛАСИЯ.
Высота должна быть на оси Y для всех графиков, а остальные
длины костей должны быть размещены по оси X. Всего у вас будет четыре графика. После того, как ваши графики будут на графике, вы должны нарисовать ЛИНИЮ НАИЛУЧШЕГО СОГЛАСИЯ.
Анализ данных
1) Какой график показывает самые сильные отношения? Другими словами, какая кость лучше всего определяет рост человека?
Как вы приняли это решение?
2) Линии наилучшего соответствия используются для экстраполяции данных.Например, вы можете использовать линию для оценки роста человека на основе длины бедренной кости. Следующий график был создан с использованием выборок 10 первокурсников колледжа.
Человек имеет бедро длиной 32 сантиметра. Используйте график, чтобы оценить рост этого человека: ________
Человек имеет бедро длиной 26 сантиметров. Используйте график, чтобы оценить рост этого человека: ________
3) На основе этих строк была разработана формула регрессии для оценки роста человека.
Для европеоидной женщины:
Высота = 2,47 * длина бедра + 54,10 плюс-минус 3,72 см.
Если у женщины длина бедра 158 см, какого роста вы ее оцените?
Инструкции:
1. Используйте данные из части 1, чтобы заполнить данные о росте и стопе в см.
1. Отметьте расстояние 30 метров, возможно, ваш инструктор уже сделал это в
прихожая.
2. Пройдите длину, считая количество шагов, и заполните таблицу
3.Рассчитайте шаг (расстояние / количество шагов)
3. Измерьте длину стопы (вы можете использовать свои измерения из части 1)
| Высота | Фут | Шагов на 30 м | (шаг) 30 / количество ступеней | |
| Тема 1 | ||||
| Тема 2 | ||||
| Тема 3 | ||||
| Тема 4 | ||||
| Тема 5 | ||||
| Тема 6 | ||||
| Тема 7 | ||||
| Тема 8 |
Анализ данных:
Создайте другой график, показывающий взаимосвязь между шагом и высотой , и график, показывающий взаимосвязь между длиной футов и шагом . Поместите длину шага по оси X, а также высоту и ступню.
длина по оси Y. Создать сюжет
баллов за каждый предмет и нарисуйте ЛИНИЮ НАИЛУЧШЕГО СООТВЕТСТВИЯ. Прикрепите график к этой странице.
Поместите длину шага по оси X, а также высоту и ступню.
длина по оси Y. Создать сюжет
баллов за каждый предмет и нарисуйте ЛИНИЮ НАИЛУЧШЕГО СООТВЕТСТВИЯ. Прикрепите график к этой странице.
1) Вы видите узор на графиках? Что кажется быть ли взаимосвязью между длиной шага и длиной ноги? (Резюме в полном предложении).
2) Используя оба набора данных, опишите, как вы могли определить рост человека, если вам известна его длина шага.
Дополнительные вопросы
4) Кража со взломом произошло, и полиция определила две пары следов на месте происшествия. преступление. Используйте показанный рисунок для оценки рост двух грабителей в зависимости от длины их стопы и шага длина. Защитите свою оценку ссылки на данные из любых графиков, которые вы создали в этом упражнении.
5) Судебно-медицинская экспертиза
ученые также могут оценить вес человека по шагам.Разработайте эксперимент, в котором вы могли бы протестировать
можно ли соотнести шаги и вес.
6) Палеонтологи финансируют «следы следов» обезьян, людей, и древние гоминиды. Особенности треки могут предоставить информацию о размере, походке и даже о том, был двуногим или четвероногим. Сравните Показаны следы человека (двуногого) и шимпанзе (четвероногого). Перечислите два сходства и два различия очевидно из изображения.
Прогнозирование типа скольжения и критического запаса прочности на однородных конечных склонах
Склон в сухих условиях
После моделирования критического уклона в программном обеспечении, вероятной поверхности скольжения и запаса устойчивости в критических условиях, а также можно наблюдать тип проскальзывания. На рис. 2a – c, если удельный вес (\ (\ gamma \)) составляет 15 кН / м 3 , сцепление ( C ) составляет 25 кН / м 2 и угол внутреннего трения (\ (\ emptyset \)) 14 ° применяется для углов наклона (\ (\ beta \)) 30, 45, 60, соответственно, коэффициент безопасности после моделирования получается равным 2. 142, 1.912 и 1.622 соответственно. Как видим, изменение геометрической формы откоса вызывает относительное изменение сил сопротивления и разрушающих сил, и возникают различные степени устойчивости запаса прочности. Как видно, коэффициент запаса прочности уменьшился с увеличением угла наклона \ (\ beta \). Следует отметить, что программное обеспечение SLOPE / W вычисляет и строит все потенциальные круги скольжения, чтобы определить коэффициент безопасности для заданных условий, и рассматривает минимально возможное значение как критический коэффициент безопасности.\ circ \), в котором значение запаса прочности против скольжения ( F s ) для критической поверхности скольжения составляет 2,142. Скользящий клин (над критической поверхностью скольжения) для этого состояния делится на 30 слоев, и информация о 12-м срезе показана в таблице 2. Также на рис. 3b представлена диаграмма свободного тела и многоугольник сил для 12-го среза.
142, 1.912 и 1.622 соответственно. Как видим, изменение геометрической формы откоса вызывает относительное изменение сил сопротивления и разрушающих сил, и возникают различные степени устойчивости запаса прочности. Как видно, коэффициент запаса прочности уменьшился с увеличением угла наклона \ (\ beta \). Следует отметить, что программное обеспечение SLOPE / W вычисляет и строит все потенциальные круги скольжения, чтобы определить коэффициент безопасности для заданных условий, и рассматривает минимально возможное значение как критический коэффициент безопасности.\ circ \), в котором значение запаса прочности против скольжения ( F s ) для критической поверхности скольжения составляет 2,142. Скользящий клин (над критической поверхностью скольжения) для этого состояния делится на 30 слоев, и информация о 12-м срезе показана в таблице 2. Также на рис. 3b представлена диаграмма свободного тела и многоугольник сил для 12-го среза.
 \ circ \))
\ circ \))В инженерном проектировании, помимо знания запаса прочности от скольжения на склоне, важно иметь информацию о типе круга разрушения с конечным уклоном.В общем, круг разрушения называется окружностью схождения , если он проходит через основание склона, и окружностью уклона , если он проходит над носком склона. Средняя точка круга (разрушение основания) возникает таким образом, что поверхность скольжения проходит на некотором расстоянии ниже носка склона (Das 2010).
На рис. 6 показаны границы каждого круга отказов в зависимости от угла наклона. Вертикальная ось – процент появления каждого круга скольжения.\ circ \)), круг отказа – только круг схождения.
Рис.6Границы наклона потенциальной окружности скольжения относительно угла наклона
На рис. 7 показано изменение числа остойчивости ( м ) в зависимости от запаса прочности ( F s ). Как видно из рисунка, с увеличением числа остойчивости коэффициент запаса прочности увеличивается для заданного угла наклона. Преимущество рис. 7 состоит в том, что при наличии числа устойчивости значение коэффициента запаса прочности и тип скольжения также могут быть определены одновременно.\ circ \)), коэффициент запаса прочности равен 1,6 (\ (F _ {\ text {s}} = 1,6 \)), а тип разрушения – окружность , наклон окружности .
Преимущество рис. 7 состоит в том, что при наличии числа устойчивости значение коэффициента запаса прочности и тип скольжения также могут быть определены одновременно.\ circ \)), коэффициент запаса прочности равен 1,6 (\ (F _ {\ text {s}} = 1,6 \)), а тип разрушения – окружность , наклон окружности .
Классификация типа скольжения по углу наклона и различным номерам устойчивости
На рисунке 8 показан другой вариант коэффициента скольжения при изменении безопасности без габаритных размеров. Использование безразмерных параметров \ (m / \ tan \ emptyset \) и \ (\ tan \ emptyset \) / F s привело к линейному уравнению между эффективными параметрами.
Рис.8Определение запаса прочности по отношению к числу остойчивости для разных углов
Чтобы определить коэффициент безопасности против устойчивости откосов, Михаловски (2002) выполнил анализ устойчивости откосов, используя кинематический подход предельного анализа для жесткого механизма вращательного обрушения, в котором поверхность разрушения в грунте принимает форму дуги логарифмической спирали. . Михаловский (2002) представил графики для определения запаса прочности, F s , по значению безразмерных параметров, \ (C / (\ Gamma) (H) (tan- \ phi) \), \ (F _ {\ текст {s}} / \ tan \ emptyset \) и углы наклона, \ (\ beta \).На практике использование диаграммы требует интерполяции и использования линейки, что отнимает много времени и не является точным. В настоящем исследовании необходимые данные были извлечены из диаграммы Михаловски (2002), а затем было разработано уравнение регрессии для решения задачи интерполяции. Результатом является линейное и нелинейное уравнение в соответствии с таблицей 3. Замечено, что нелинейное уравнение представляет соответствующие результаты, в которых среднеквадратичная ошибка (RMSE) меньше, чем у линейного уравнения и коэффициента детерминации ( R 2 ) больше, чем полученное линейное уравнение.На следующем этапе мы сравнили предложенный метод с выходными данными программного обеспечения SLOPE / W (Таблица 4).
. Михаловский (2002) представил графики для определения запаса прочности, F s , по значению безразмерных параметров, \ (C / (\ Gamma) (H) (tan- \ phi) \), \ (F _ {\ текст {s}} / \ tan \ emptyset \) и углы наклона, \ (\ beta \).На практике использование диаграммы требует интерполяции и использования линейки, что отнимает много времени и не является точным. В настоящем исследовании необходимые данные были извлечены из диаграммы Михаловски (2002), а затем было разработано уравнение регрессии для решения задачи интерполяции. Результатом является линейное и нелинейное уравнение в соответствии с таблицей 3. Замечено, что нелинейное уравнение представляет соответствующие результаты, в которых среднеквадратичная ошибка (RMSE) меньше, чем у линейного уравнения и коэффициента детерминации ( R 2 ) больше, чем полученное линейное уравнение.На следующем этапе мы сравнили предложенный метод с выходными данными программного обеспечения SLOPE / W (Таблица 4).
Чтобы оценить коэффициент стабильности безопасности для каждого из методами Моргенштерна – Прайса, Янбу, Бишопа и ординарного (Феллениус или Шведский круг) уравнения линейной регрессии также были извлечены с помощью SPSS (SPSS, версия 22 2015).Результаты этих вычислений показаны в Таблице 5. Следует отметить, что эти уравнения получены для смоделированного диапазона \ (30 <\ beta <75, 14 <\ emptyset <17, 22 <\ gamma <25 \, {\ текст {и}} \, 15 Согласно Таблице 5, следует отметить, что предложенные уравнения регрессии очень точны при оценке коэффициента безопасности устойчивости откоса. Предлагаемое уравнение для метода Джанбу имеет наивысшую точность с RMSE = 0. Коэффициент запаса численного и регрессионного метода, a метод Моргенштерна – Прайса, b метод Янбу, c метод Бишопа и d обычный метод Калманн (1875) предложил аналитический метод определения запаса прочности, при котором поверхность разрушения создается на плоскости скольжения вдоль склона. Другими словами, поверхность скольжения является линейной, а не круглой для простоты в двумерном режиме. Видно, что с увеличением угла наклона \ (\ beta \) коэффициент запаса прочности, полученный методом Кульманна, аппроксимируется методами расчета запаса прочности с методом анализа конечного уклона с круговой поверхностью разрушения, такой как как Бишоп, Моргенштерн-Прайс, Янбу и Михаловски. Таким образом, можно сказать, что метод Калмана дает хорошие результаты для крутых или почти вертикальных склонов, но не дает удовлетворительных результатов для пологих склонов (Таблица 6).\ circ, \, \ frac {h} {H} = 0,6875 \) Как показано на рис. 11a, b, наблюдается изменение уровня воды, склон полностью затоплен, и полное погружение достигается при опускании уровня воды на 5,5 м вниз. Коэффициент запаса прочности за счет снятия нагрузки за счет веса воды на склоне, который находится в направлении устойчивости до падения уровня воды, снизился на 41,42%. На рис. 12 показана другая расчетная схема для проверки устойчивости и определения запаса прочности склонов, подверженных падению уровня воды. На этом графике вертикальная ось показывает коэффициент перепада ( h / H ), где ( h ) – это величина падения уровня поверхности воды (высота просадки), а ( H ) – высота падения. склон. Можно заметить, что за счет уменьшения уровня поверхности воды на склоне из-за удаления веса воды на склоне коэффициент безопасности стал меньше (при условии, что давление поровой воды не рассеивается).\ circ \). Из рисунка видно, что когда значение ( h / H ) приближается к носку уклона ( h / H = 1), коэффициент запаса прочности уменьшается за счет уменьшения числа устойчивости. Следовательно, можно сказать, что коэффициент запаса прочности уменьшается при понижении уровня воды (поровое давление воды не рассеивается), но с увеличением числа устойчивости он будет в более стабильном состоянии. Изменение запаса прочности ( F s ) относительно потери относительного уровня воды ( h / H ) для состояния (\ (m = 0.\ circ \)) 1) Направление связи Регрессия даст нам эти свойства, а также позволит нам конкретизировать
прогнозы относительно одной переменной, основанные на том, что мы знаем о другой
Переменная. Прогноз – если мы знаем, что две переменные сильно связаны,
тогда мы сможем предсказать ценность одного, основываясь на значении другого. например, если вы знаете, что ультразвуковые измерения головы ребенка
положительно коррелирует с массой тела при рождении, то вы можете
обоснованное предположение о весе ребенка при рождении путем измерения веса ребенка
головка от УЗИ Начнем с обзора старой геометрии.Рассмотрим следующее
график. Таким образом, когда X увеличивается на 1, Y увеличивается на 0,5. Это называется уклон .
(б). Это постоянная величина. Пересечение (a) – это значение Y, когда
X = 0. Это тоже константа. Мы можем описать линию следующим линейным уравнением: Y = bX + a —> Y = (0,5) X + 1,0 другими словами, используя линейное уравнение, мы можем определить значение
Y, если мы знаем значения X, b и a – напомним, что предсказание Y на основе X – одна из основных задач, которые
глава все о Хорошо, теперь вернемся к нашим диаграммам рассеяния. Теперь рассмотрим случай, когда корреляция не идеальна. Также можно отметить
отдельные точки данных путем добавления категориальной переменной в “набор”
маркеры по полю.
. Что значит быть линией, которая «лучше всего соответствует» данным? Итак, теперь у нас есть уравнение регрессии для данных из нашего примера.Мы можем использовать это
уравнение для прогнозирования Y при заданных значениях X. Однако нам нужно больше
информация для завершения нашего описания взаимосвязи между
две переменные. ().
Стандартная ошибка оценка описывает типичную ошибку при использовании оценки Y. Чтобы получить это, мы посмотрим на каждую точку и сравним фактическое значение Y с прогнозируемым. Ошибка SS = общая квадратичная ошибка = Мы получаем значения из строки, а значения Y из фактических данных.
точки Нам нужно сделать это для всех значений a и b. Как нам вычислить стандартную ошибку оценки ? SS ошибка = Затем мы разделим это на наши степени свободы (которые
дает нам меру дисперсии или среднеквадратичную ошибку) помните, что df = n – 2 В итоге мы получаем: знак равно22 (Х) + 0,68 S ошибка =
знак равно
знак равно
= . Другой способ вычисления ошибки S – использовать корреляционный
информация (если она у вас есть под рукой). Ошибка SS = (1 – r 2 ) SS Y =
(1 – (+0,875) 2 ) (4) = (1 – 0,766) (4) = 0,9375 S ошибка =
знак равно
= .559 Сумма остатков всегда должна быть равна 0 (как и среднее значение).Этот
потому что линия регрессии наименьших квадратов разделяет данные пополам, наполовину
ошибки находится выше линии, а половина – ниже линии. Однако, помимо суммирования до нуля, мы также хотим, чтобы остатки
быть распределенными случайным образом. То есть не должно быть рисунка
остатки. Если есть закономерность, это может означать, что их больше, чем
простая линейная связь между двумя переменными. Остаточные графики – очень полезный инструмент для изучения взаимосвязи даже
дальше.По сути, это диаграммы рассеяния остатков () от переменной Explanatory (X) (примечание: графики
остатков от других переменных также может быть поучительным). Диаграмма рассеяния показывает красивую линейную зависимость. Остаточный сюжет
показывает Диаграмма рассеяния также показывает хорошую линейную зависимость. Тем не менее
остаточный Диаграмма рассеяния показывает, что может быть линейной зависимостью.Остаток Общая линейная модель возвращает выборки и проблемы популяций в
рисунок. Линия регрессии наименьших квадратов, которую мы обсуждали до
этот момент можно считать выборочной оценкой истинных уравнение регрессии для населения. Обозначения немного изменятся.Теперь обратимся к наклону
линия как B 1 и точка пересечения как
В 0 . Итак, уравнение для линии
это: Как обсуждалось выше, нам также нужна мера погрешности (изменчивости)
вокруг линии. Мы обозначим это греческой буквой эпсилон. Так
полное уравнение будет: Это уравнение описывает статистическую модель данных. В
части уравнения, иногда описываемые как состоящие из FIT и
ОСТАТОЧНЫЙ. Проверка регрессионной модели в основном сводится к проверке того,
наклон равен нулю. Шаги аналогичны предыдущим тестам
гипотезы. То есть, если наклон равен нулю, то нет никакой связи между X и
Ю. Степени свободы: df = n – 2 (где n = количество пар XY) Есть несколько тестов модели. Самые важные два – это
ANOVA и один из t-критериев коэффициента. Для двумерной регрессии эти
два теста дают одинаковый результат (F из
ANOVA – это квадрат T из T-теста). Для наших текущих целей
мы просто сосредоточимся на t-тесте наклона. Вот разбивка компонентов таблицы ANOVA: SPSS также выполнит t-тест, чтобы проверить гипотезу о перехвате.
(H 0 : B 0 = 0), но эти
результаты используются редко. Если вы хотите следовать примеру с файлом данных SPSS,
основан на, вы можете скачать height.sav
файл данных. Мы также можем использовать нашу технику регрессии для проверки значительного
связь между двумя переменными. Помните, что когда мы выполняем
регрессии, мы вычисляем наклон (b) для линии “наилучшего соответствия”, чтобы описать
данные. SPSS предоставляет тест (t-тест), чтобы определить, является ли наклон (b)
значительно отличается от 0 (что указывает на наличие линейного
отношения между двумя переменными). Для обзора: Примечание: вы можете добавить более одной независимой переменной за раз.
Это называется «множественная регрессия». Посмотрите на вывод ниже. Вывод команды Regression включает четыре
разные значения: 075 и R 2 = 0,969 (таблица 5). Метод Бишопа обеспечивает меньшую точность, чем другие методы. Но в методе Бишопа максимальная ошибка составляет 1,36%, и это можно игнорировать. В исследовании Whitman and Bailey (1967) максимальная ошибка F s составляет 7%, а средняя ошибка составляет 2%. Таким образом, можно использовать упрощенный метод Бишопа из-за его простоты и точности в расчетах. В дополнение к указанным выше критериям, для проверки точности предложенных уравнений регрессии использовалась диаграмма разброса данных на рис.9a – d.
075 и R 2 = 0,969 (таблица 5). Метод Бишопа обеспечивает меньшую точность, чем другие методы. Но в методе Бишопа максимальная ошибка составляет 1,36%, и это можно игнорировать. В исследовании Whitman and Bailey (1967) максимальная ошибка F s составляет 7%, а средняя ошибка составляет 2%. Таким образом, можно использовать упрощенный метод Бишопа из-за его простоты и точности в расчетах. В дополнение к указанным выше критериям, для проверки точности предложенных уравнений регрессии использовалась диаграмма разброса данных на рис.9a – d. {3}, \, H = 8 \, {\ text {m}} \).
{3}, \, H = 8 \, {\ text {m}} \). Кроме того, поверхность скольжения изменилась с касания – средней точки окружности на окружности наклона .
Кроме того, поверхность скольжения изменилась с касания – средней точки окружности на окружности наклона .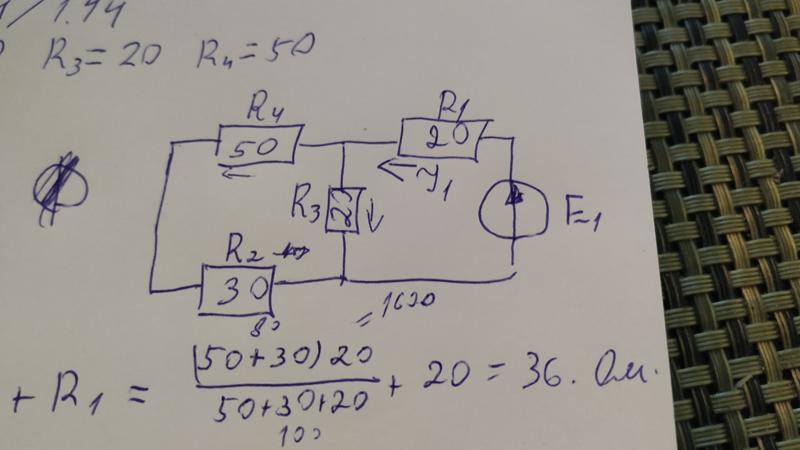
Психология 340: Линейная регрессия
Предупреждения о регрессии Основы
Процедуры корреляции и регрессии имеют ряд общих черт.
Как мы обсуждали в прошлый раз, корреляция говорит нам о трех характеристиках взаимосвязи.
между X и Y Корреляция описывает отношения между двумя непрерывными
переменные
И корреляция, и регрессия проверяют нулевую гипотезу о том, что два
переменные не зависят друг от друга
Регрессия позволяет прогнозировать оценки по одной переменной с учетом
набрать еще на
2) Форма связи
3) Степень родства 
Уравнение для линии
при X = 0, Y = 1
при X = 1, Y = 1,5
при X = 2, Y = 2,0
при X = 3, Y = 2,5
при X = 4, Y = 3,0 Диаграммы рассеяния
 Начнем со случая
идеальная положительная корреляция (r = 1.0).
Начнем со случая
идеальная положительная корреляция (r = 1.0). Когда мы проводим регрессионный анализ, мы пытаемся найти
линия (и линейное уравнение), которая наилучшим образом соответствует точкам данных. За это
пример это довольно просто. Есть только одна возможная линия, которая делает
смысл соответствовать этому набору данных. Теперь это не так просто. Ясно, что ни одна прямая линия не подходит для всех данных
точка (то есть вы не можете провести одну линию через все данные
точки). На самом деле нетрудно представить несколько различных возможных
линии, соответствующие этим данным. Нам нужна линия (и линейная
уравнение) лучше всего подходит . Получение SPSS для построения диаграммы рассеяния и нанесения линии регрессии наименьших квадратов на нашу
диаграмма рассеяния
Создание диаграммы рассеяния
Подгонка к линии  В
предсказатель идет по оси X (если вы смотрите на корреляции, скорее
чем регрессии, не имеет значения, что куда идет). Например,
если вы хотите прогнозировать вес с учетом роста, вам следует прибавить в весе
ось Y и высоту по оси X.
В
предсказатель идет по оси X (если вы смотрите на корреляции, скорее
чем регрессии, не имеет значения, что куда идет). Например,
если вы хотите прогнозировать вес с учетом роста, вам следует прибавить в весе
ось Y и высоту по оси X.
Это откроет окно вывода и вставит вашу диаграмму рассеяния. Выберите “простую” диаграмму рассеяния Чтобы назначить переменные X и Y, вам нужно выбрать их из переменной
листинг и вставьте их в оси X и Y.  Напомним, что для открытия редактора диаграмм нужно удвоить
щелкните интересующий график.Откроется новое окно с графиком.
редактор.
Напомним, что для открытия редактора диаграмм нужно удвоить
щелкните интересующий график.Откроется новое окно с графиком.
редактор. Регрессия наименьших квадратов
Вычисление остатков (погрешность вокруг линии)
Любое полное описание прогнозирующей связи между X и Y
необходимо включить меру погрешности вокруг линии.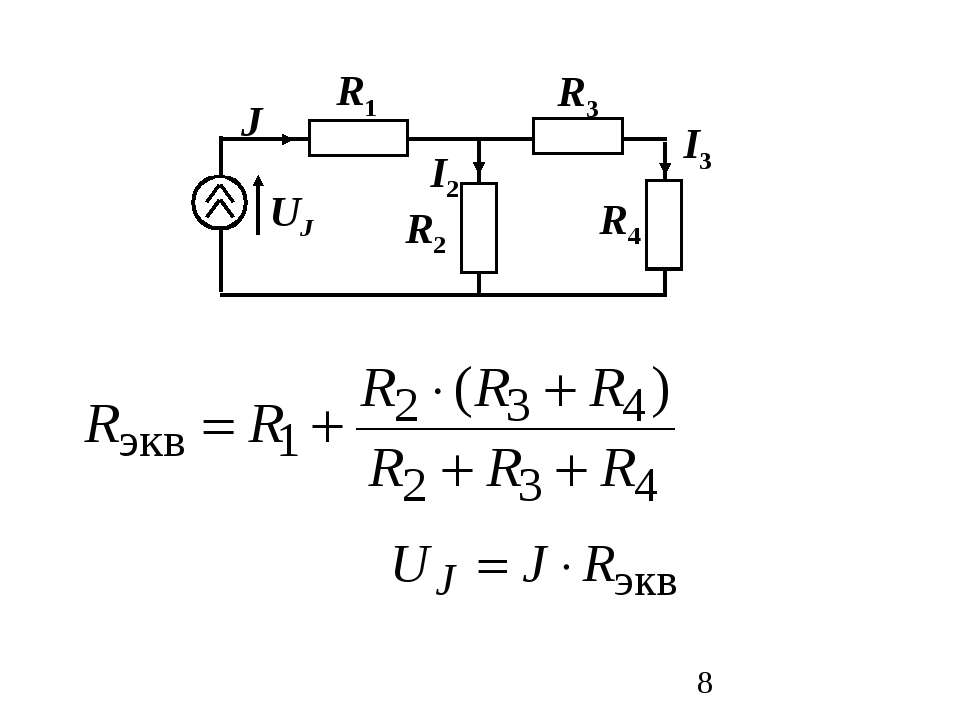
Рассмотрим эти две диаграммы рассеяния. Уравнение для
линия идентична для обоих, однако взаимосвязь между переменными
(X&Y) разные.В первом сюжете отношения слабее
относительно второго. Это потому, что вокруг
строка в первой. Вот почему мы должны сообщить не только уравнение для
линия, но и мера погрешности.  значение Y (которое называется (произносится как “Y-шляпа”)
значение Y (которое называется (произносится как “Y-шляпа”) расстояние = Сначала нам нужна наша общая квадратная ошибка
 559
559 Остаточные участки
 Рассмотрим три примера ниже (примечание: на самом деле эти примеры показывают
остатки, преобразованные в z-баллы).
Рассмотрим три примера ниже (примечание: на самом деле эти примеры показывают
остатки, преобразованные в z-баллы).
что остатки случайным образом падают выше и ниже линии.Критически
в остатках, кажется, нет заметной закономерности.
график показывает
что остатки увеличиваются с увеличением X. Это говорит о
, что
изменчивость вокруг линии не является постоянной для значений X.
сослался на
как на нарушение
однородность дисперсии.
сюжет, однако, предполагает, что нелинейная зависимость может быть более
подходящие (посмотрите, как изогнутый узор появляется на остаточном графике). Получение остаточных графиков в SPSS
Это делается, когда SPSS выполняет регрессионный анализ.  На
внизу окна регрессии есть кнопка с надписью «сохранить».
На
внизу окна регрессии есть кнопка с надписью «сохранить». Это окно открывается при нажатии кнопки сохранения.Нажмите сохранить
поле остатков в правом верхнем углу. Общая линейная модель
 Подгонка состоит из линейного уравнения, а ОСТАТОК равен
ошибка (непостоянство, не объясняемое линейным уравнением).
Подгонка состоит из линейного уравнения, а ОСТАТОК равен
ошибка (непостоянство, не объясняемое линейным уравнением). Использование регрессии для проверки взаимосвязи
Нулевая гипотеза, H 0 : B 1 = 0.
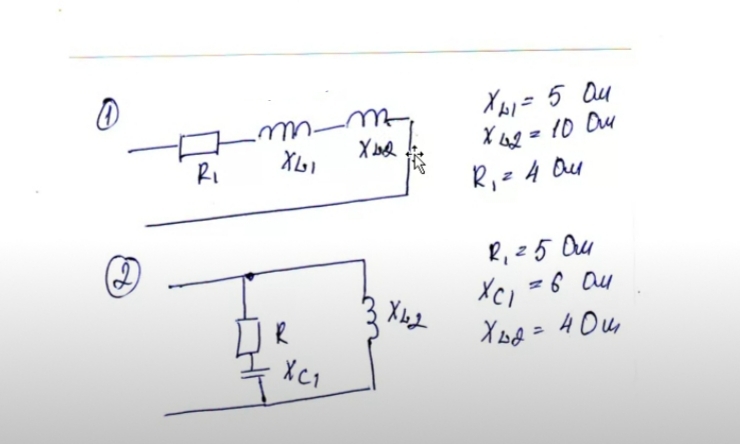
Использование SPSS для преобразования регрессии
 Это более сложная тема,
мы можем поговорить об этом подробнее позже в ходе курса.А пока просто сделай
регрессии с одной независимой переменной за раз.
Это более сложная тема,
мы можем поговорить об этом подробнее позже в ходе курса.А пока просто сделай
регрессии с одной независимой переменной за раз. Примечание: регрессионный анализ также дает нам
возможность сделать больше, чем просто получить уравнение для линии. Потому что
это наш вывод будет содержать много информации. Будьте готовы к
должны просеять его, чтобы получить нужную нам информацию.