Расчёт частоты резонанса колебательного контура
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
– Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
– Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
– Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
– Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.
Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке,
что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 = .
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора
индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1,
он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения
В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Частота резонанса колебательного контура LC. |
Расчёт ёмкости:
Ёмкость для колебательного контура LC |
Расчёт индуктивности:
Индуктивность для колебательного контура LC |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
tel-spb.ru
Формулы расчета резонансной частоты колебательного контура: амплитуда резонанса
Галилео Галилей, исследуя маятники и музыкальные струны, описал явление, которое впоследствии стали называть резонансом. Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.
Резонанс
Эффект резонанса
Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В. Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка.
- электродвигатель;
- механизм, превращающий вращение в возвратно-поступательное движение;
- ЛАТР – лабораторный автотрансформатор;
- медная пружина из проволоки с набором грузиков;
- направляющая для пружины.
Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.
Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (~30 см).
Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден. Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.
Пружинный маятник
Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.
Определение колебательного контура
Резонансные явления, отмеченные в электротехнике, ярко выражены в схемах колебательных контуров (КК). Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
- конденсатора;
- катушки индуктивности;
- источника тока.
Внимание! Выводы элементов схемы могут соединяться друг с другом параллельно или последовательно. Все зависит от того, какого результата нужно добиться от резонанса в КК.
Подключение к цепи индуктивной катушки
Включение в ёмкостную цепь катушки индуктивности сразу превращает её в КК. В зависимости от схемы подключения, различают два вида КК 1 класса: параллельный и последовательный.
Параллельный КК
В данной схеме конденсатор С соединён с катушкой L параллельно. Если заряженный конденсатор присоединить к катушке, то энергия, запасённая в нём, передастся ей. Через индуктивную катушку L потечёт ток, вызывая электродвижущую силу (ЭДС).
ЭДС самоиндукции L будет направлена на снижение тока в параллельной цепи. Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
Параллельный КК
К сведению. Если бы в такой цепи отсутствовали потери, то такие колебания никогда не стали затухать. На практике, продолжительность процесса зависит от потери энергии. Чем больше потери, тем меньше длительность колебаний.
Параллельное соединение C и L вызывает резонанс токов. Это значит, что токи, проходящие через C и L, выше по значению, чем ток через сам контур, в конкретное число раз. Это число носит название добротности Q. Оба тока (емкостной и индуктивный) остаются внутри цепи, потому что они находятся в противофазе, и происходит их обоюдная компенсация.
Стоит отметить! На fрез величина R КК устремляется к бесконечности.
Последовательный КК
В этой схеме соединены последовательно друг с другом катушка и конденсатор.
Последовательный КК
В такой схеме происходит resonance напряжений, R контура устремляется к нулю в случае образования резонансной частоты (fрез). Это позволяет использовать подобную систему резонанса в качестве фильтра.
Резонансная частота
При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:
- с увеличением f – ёмкостное сопротивление уменьшается, а индуктивное увеличивается;
- с уменьшением f – ёмкостное сопротивление увеличивается, а индуктивное уменьшается.
Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.
Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным.
Резонансная частота формула, которой имеет вид:
fрез = 1/2π*√L*C,
где:
- L – индуктивность, Гн;
- C – ёмкость, Ф.
Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.
Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.
Пример интерфейса онлайн калькулятора LC-контура
Применение колебательных контуров
Подробный расчет колебательного контура позволяет точно подбирать величину необходимых элементов КК. Это позволяет использовать их в схемах электроники в виде:
- частотных фильтров – в радиоприёмниках, генераторах сигналов, преобразователях и выпрямителях;
- колебательных контуров – для выделения и настройки на определённую частоту станции вещания;
- силовых resonance-фильтров – для формирования напряжения синусоидальной формы.
На самолётах гражданской авиации КК применяется в блоках регулировки частоты генераторов.
Условие отсутствия резонанса
Для того чтобы возник резонанс формула которого для тока равна ω0*C = 1/ ω0*L, необходимо выполнения этого равенства. Существуют условия для невозможности появления этого эффекта, а именно:
- отсутствие у системы собственных колебаний;
- невозможность совпадения частоты внешнего воздействия с собственной частотой системы.
Амплитуда резонанса
В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.
Амплитуда тока
Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.
В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:
x = xL – xC.
Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.
Схема (а) и резонансные кривые (б) для резонанса напряжений
Амплитуда напряжения
Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.
Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е – I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е.
Схема (а) и резонансные кривые (б) для резонанса токов
Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.
Видео
amperof.ru
Формулы расчета резонансной частоты колебательного контура
Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура. Подобрав параметры элементов цепи, можно производить частоты свыше 500 МГц. Схемы используются в ВЧ-генераторах, высокочастотном нагреве, телевизионных и радиоприемниках.
Колебательный контур
Колебательный контур
Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.
Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.
Работа колебательного контура
Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.
Что будет, если в цепь включить индуктивную катушку:
- При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
- Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
- Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;
Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.
- После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.
Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.
Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.
Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.
Затухающие колебания
Резонанс
Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное. Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.
Индуктивное сопротивление прямо пропорционально частоте:
X(L) = 2π x f x L,
а емкостное сопротивление обратно пропорционально этому показателю:
X(C) = 1/(2π x f x C).
Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная.
При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.
Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.
Резонанс LC-цепи
Для расчета резонансной частоты колебательного контура учитывается следующее условие:
X(L) = X(C).
Следовательно, 2π x f x L = 1/(2πx f x C).
Отсюда получается формула резонансной частоты:
f = 1/(2π x √(L x C)).
Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.
Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.
LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.
Видео
Оцените статью:jelectro.ru
Электротехника: Резонансная частота.
Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты. Рисунок 1 – Параллельный колебательный контурРисунок 2 – Последовательный колебательный контур
Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют – резонансом токов, резонанс в последовательном контуре – резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:

Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:
electe.blogspot.com
Последовательный колебательный контур | Резонанс напряжений
Обозначение на схеме
Последовательный колебательный контур – это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно. На схемах идеальный последовательный колебательный контур обозначается вот так:
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R – это суммарное сопротивление потерь катушки и конденсатора
L – собственно сама индуктивность катушки
С – собственно сама емкость конденсатора
Колебательный контур и генератор частоты
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
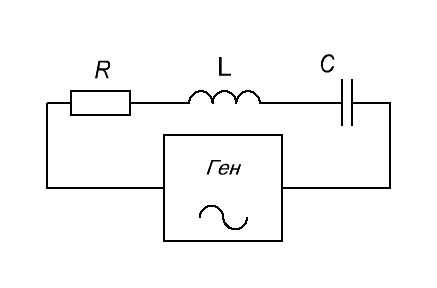
Генератор у нас будет выдавать синус.
Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
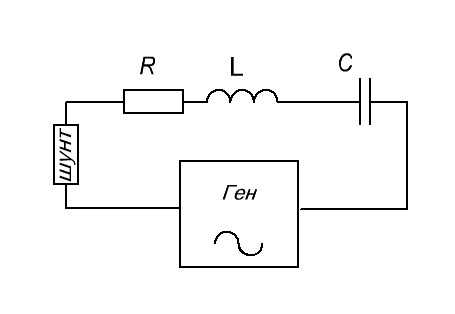
А вот и сама схема в реальности:

Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R – это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно “прячется” внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта Uш , а также снимая осциллограмму с самого генератора UГЕН.
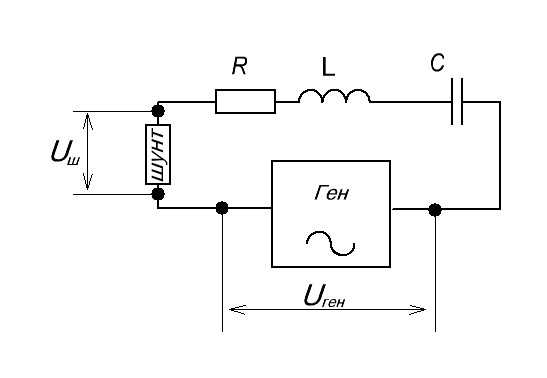
С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты на сопротивление колебательного контура
Итак, погнали. В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма – это напряжение с генератора частоты, а желтая осциллограмма – отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
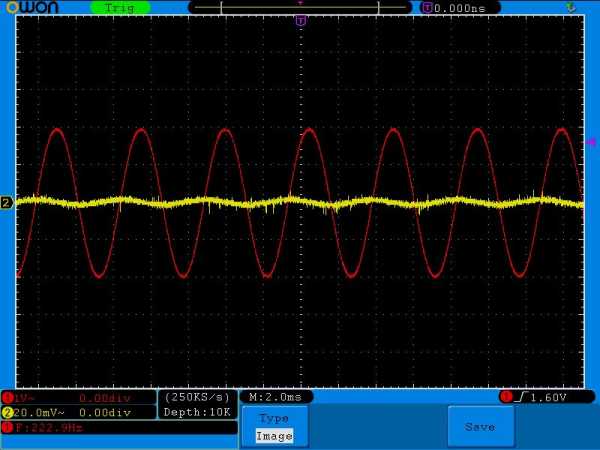
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
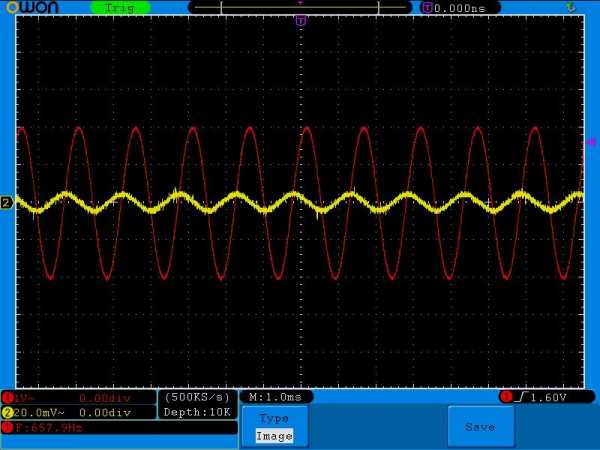
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.
Добавляем частоту. 2 Килогерца
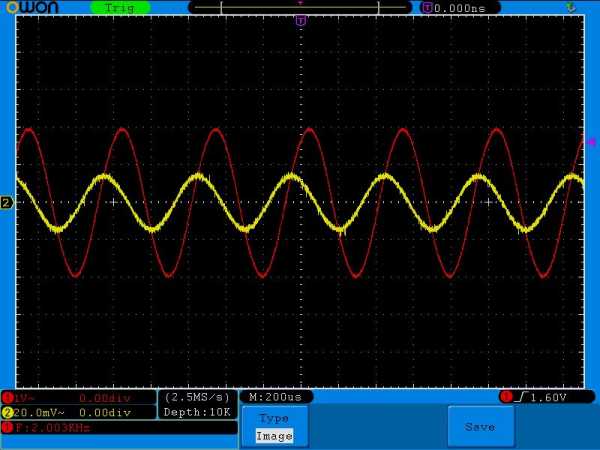
Сила тока стала еще больше.
3 Килогерца
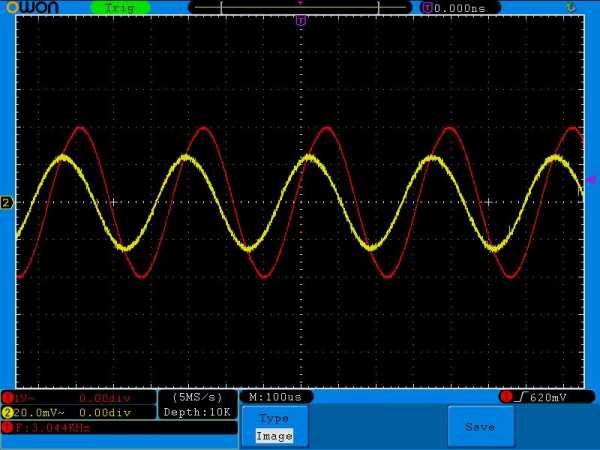
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
4,25 Килогерц
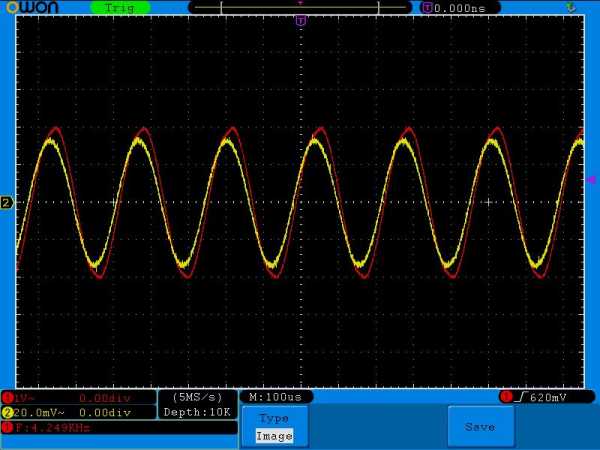
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.
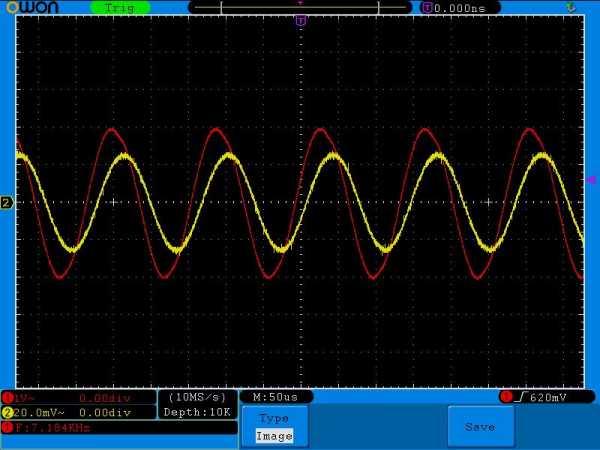
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
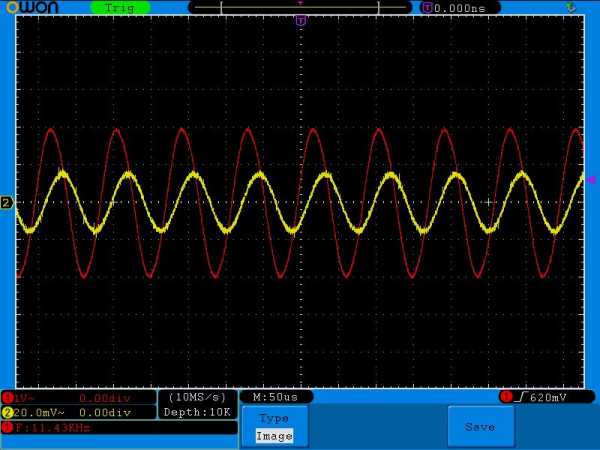
Сила тока начинает падать, а сдвиг фаз увеличивается.
22 Килогерца
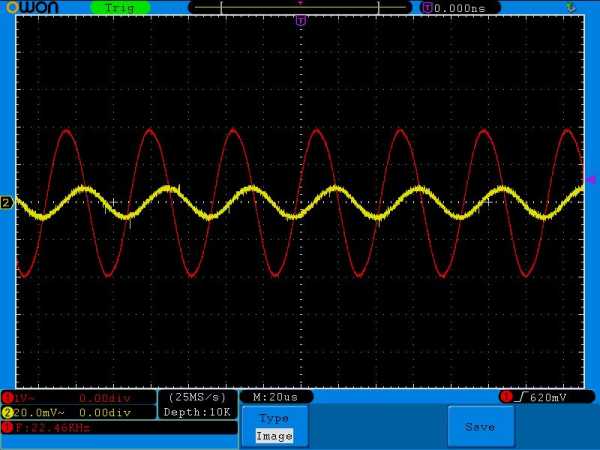
74 Килогерца
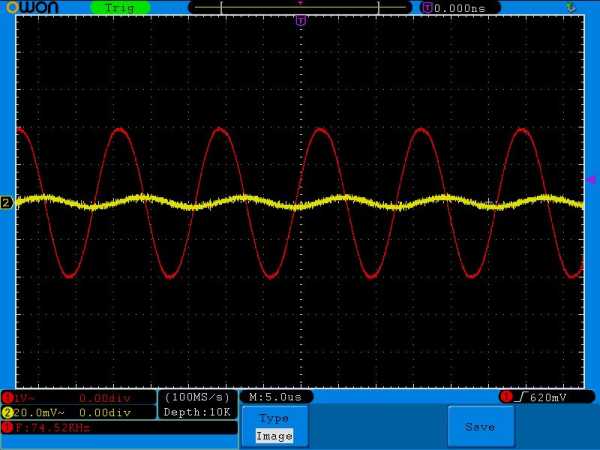
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса.
Не будем углубляться в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:

И замеряем нашу емкость:

Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор – это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
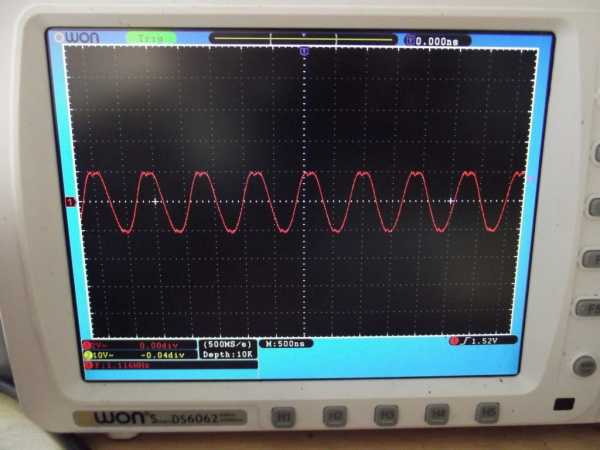
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол 😉
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
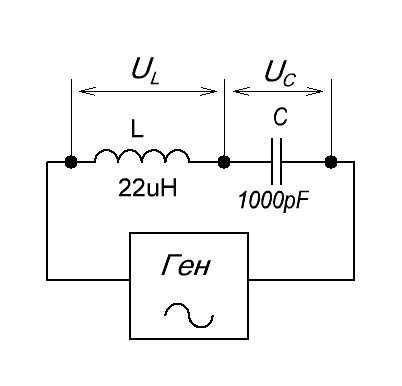
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
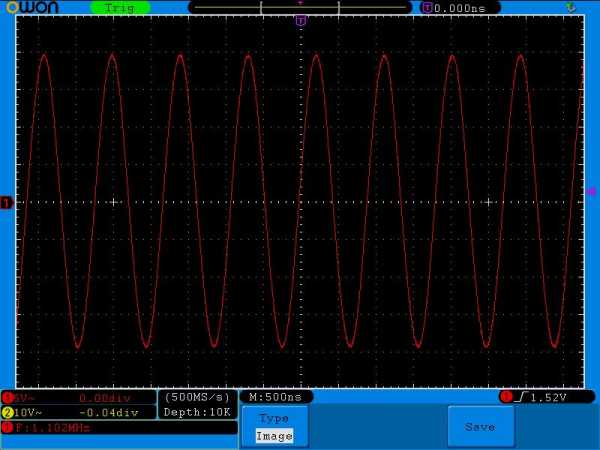
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию или с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:


Как видите – полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока – увы! Поэтому последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Давайте обобщим, что у нас получилось в этих опытах.
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Добротность
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
где
R – сопротивление потерь в контуре, Ом
L – индуктивность, Генри
С – емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура – это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса – индуктивную составляющую тока.
www.ruselectronic.com
Расчет колебательного контура
Практический расчет последовательного или параллельного LC контура.
Доброго дня уважаемые радиолюбители!
Сегодня мы с вами рассмотрим порядок расчета LC контура.
Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.
LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур) или последовательно (последовательный контур), как на рис.1:
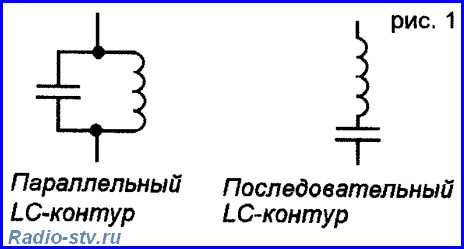
Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:
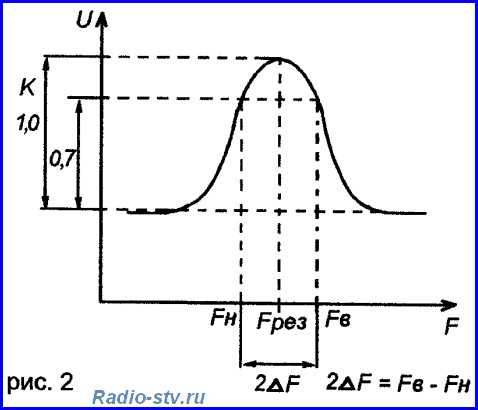
На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.
Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:
L=(159,1/F)2/C где:
L – индуктивность катушки в мкГн;
С – емкость конденсатора в пФ;
F – частота в МГц
Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:
L=(159,1/1)2 /1000 = 25 мкГн
Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать,, а вот индуктивность нужно сделать самостоятельно.
Рассчитать число витков для катушки без сердечника можно по такой формуле:
N=32 *√(L/D) где:
N – требуемое число витков;
L – заданная индуктивность в мкГн;
D – диаметр каркаса в мм, на котором предполагается намотать катушку.
Предположим, диаметр каркаса – 5 мм, тогда:
N=32*√(25/5) = 72 витка.
Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.
В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:
N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка. То есть, в таком случае на потребуется намотать на катушку 43 витка провода.
radio-stv.ru
Coil32 – Собственный резонанс однослойной катушки
На заре развития радиотехники было обнаружено, что катушка не идеальная индуктивность. На определенной частоте она входит в режим резонанса даже при отсутствии внешней емкости, а выше этой частоты импеданс катушки носит уже емкостный характер. Для объяснения этого явления предположили, что кроме индуктивности реальная катушка обладает еще собственной емкостью (предположительно между соседними витками) и реальную катушку стали представлять в виде модели из сосредоточенных RLC элементов, в которой L — индуктивность, C — собственная емкость, названная паразитной, а с помощью активного R учитываются различные потери в катушке. Такая модель катушки имеет одну резонансную частоту, которую назвали частотой собственного резонанса. Долгое время эта модель всех устраивала и стала классической моделью реальной катушки во всех учебниках.
Ведь катушки в подавляющем большинстве практических применений работают на частотах намного ниже частоты собственного резонанса и задачей конструктора является, по сути, обеспечение этого условия. При этом большинство инженеров с этой целью пытались уменьшить эту самую “межвитковую” паразитную емкость. В случае же, если катушка работает на частотах близких к собственному резонансу, как например в спиральных резонаторах или катушках Теслы, RLC-модель дает неверные результаты, но для таких случаев были разработаны альтернативные алгоритмы расчета и все остались довольны не особо задумываясь о причинах таких нестыковок. В нашу цифровую эпоху появились программы, которые дали возможность моделировать поведение любых высокочастотных устройств с высокой степени точности — так называемые электромагнитные симуляторы. Это мощные пакеты типа CST Studio, HFSS и многие другие. Давайте проведем исследование однослойной спиральной катушки в программе HFSS. В первой модели мы поместим катушку над идеальной проводящей поверхностью и запитаем от точечного источника с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. Расчет будем вести в режиме HFSS Design, использующий метод конечных элементов.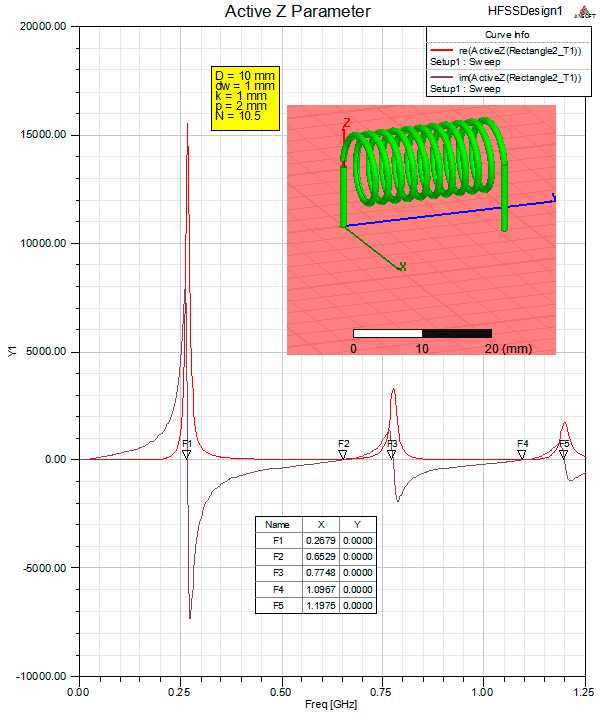 Вторую катушку рассчитаем методом HFSS Design-IE, использующий метод моментов. В отличии от популярных у радиолюбителей симуляторов на основе ядра NEC, например MMANA, здесь сегментация идет не на отрезки провода, а по его поверхности на элементарные треугольные площадки. При такой сегментации для успешного расчета требуется не менее 8-16 Гб оперативной памяти компьютера. Запитаем катушку через короткие выводы от такого же источника. Поскольку катушка не заземлена, в этой модели первый резонанс – полуволновой.
Вторую катушку рассчитаем методом HFSS Design-IE, использующий метод моментов. В отличии от популярных у радиолюбителей симуляторов на основе ядра NEC, например MMANA, здесь сегментация идет не на отрезки провода, а по его поверхности на элементарные треугольные площадки. При такой сегментации для успешного расчета требуется не менее 8-16 Гб оперативной памяти компьютера. Запитаем катушку через короткие выводы от такого же источника. Поскольку катушка не заземлена, в этой модели первый резонанс – полуволновой.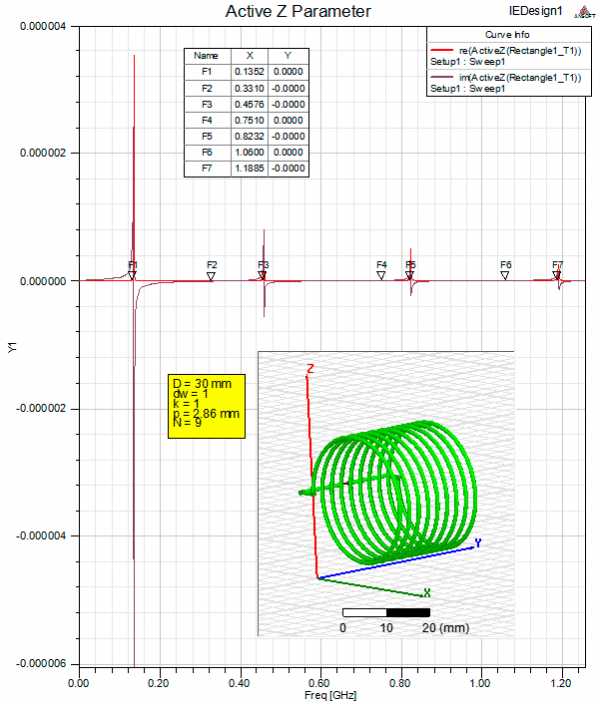 В результате исследования мы получили графики импеданса на зажимах источника относительно частоты. Из графиков видно, что у катушки не один, а множество резонансов. Из этого следует вывод, что наша катушка — это совсем не одиночный LC-контур с собственной индуктивностью и паразитной емкостью в виде сосредоточенных элементов, как принято считать, а длинная линия с распределенными параметрами. Такая линия состоит из одного провода, но это не должно никого смущать. То, что в даже одиночном проводе наблюдаются волновые резонансные явления, хорошо иллюстрирует пример полуволнового вибратора Герца. Ведь волновые явления как в длинных линиях, так и в вибраторе отображают тот факт, что электромагнитное взаимодействие распространяется с конечной скоростью. На то чтобы электромагнитное взаимодействие «добралось» от одного конца провода до другого затрачивается определенное время, и когда это время сравнимо с периодом колебаний рабочей частоты возникают явления резонанса. И катушка в этом плане недалеко ушла от вибратора, поскольку несмотря на малые ее габариты, длина провода, которым она намотана, может иметь величину сравнимую с длиной волны. Частоту собственного резонанса вибратора мы можем довольно легко определить зная его длину, учтя коэффициент укорочения. В катушке, кроме того, необходимо учесть связь между витками.
В результате исследования мы получили графики импеданса на зажимах источника относительно частоты. Из графиков видно, что у катушки не один, а множество резонансов. Из этого следует вывод, что наша катушка — это совсем не одиночный LC-контур с собственной индуктивностью и паразитной емкостью в виде сосредоточенных элементов, как принято считать, а длинная линия с распределенными параметрами. Такая линия состоит из одного провода, но это не должно никого смущать. То, что в даже одиночном проводе наблюдаются волновые резонансные явления, хорошо иллюстрирует пример полуволнового вибратора Герца. Ведь волновые явления как в длинных линиях, так и в вибраторе отображают тот факт, что электромагнитное взаимодействие распространяется с конечной скоростью. На то чтобы электромагнитное взаимодействие «добралось» от одного конца провода до другого затрачивается определенное время, и когда это время сравнимо с периодом колебаний рабочей частоты возникают явления резонанса. И катушка в этом плане недалеко ушла от вибратора, поскольку несмотря на малые ее габариты, длина провода, которым она намотана, может иметь величину сравнимую с длиной волны. Частоту собственного резонанса вибратора мы можем довольно легко определить зная его длину, учтя коэффициент укорочения. В катушке, кроме того, необходимо учесть связь между витками.
В учебниках по электродинамике [1] можно найти описание работы спиральных волноводов с поверхностными электромагнитными (ЭМ) волнами, распространяющимися вдоль провода спирали. Такие волноводы применяются как замедляющие структуры в спиральных антеннах и лампах бегущей волны. Длина одного витка и шаг намотки у них сравним с длиной волны. В частности, у спиральной антенны длина витка L равна длине волны, а шаг намотки p равен четверти длины волны.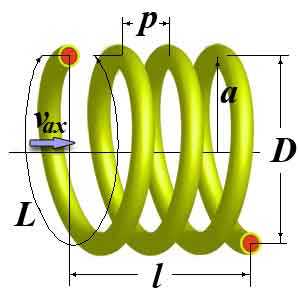 Фазовая скорость волны вдоль оси спирального волновода значительно ниже скорости света, на чем и основано его применение как замедляющей структуры.
Фазовая скорость волны вдоль оси спирального волновода значительно ниже скорости света, на чем и основано его применение как замедляющей структуры.
| [1] |
где:
- vax – скорость волны вдоль оси спирали
- с – скорость света
Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, поскольку влияние витков друг на друга минимально и ЭМ-волна распространяется вдоль провода такой спирали, так же как и у вибратора. Отметим, что фазовая скорость ЭМ волны относительно провода спирали в таком волноводе близка к скорости света.
В нашей же катушке, и длина отдельного витка, и даже длина всей намотки, и тем более шаг намотки намного меньше длины волны. В этом случае, кроме основной моды в таком спиральном волноводе существуют высшие моды колебаний, распространяющиеся непосредственно вдоль ее оси. Другими словами, ЭМ волна распространяется не только вдоль длины провода, но часть ее «перепрыгивает от витка к витку». Относительная фазовая скорость вдоль оси катушки определяется следующим приближенным выражением:
| [2] |
где:
- λ0 – длина волны рабочей частоты в свободном пространстве
Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны. По сути, катушка — тот же спиральный волновод с медленными волнами, но работающий в другом режиме колебаний. Во избежании различных спекуляций отметим то обстоятельство, что благодаря наличию высших мод, волна “добирается” до другого конца катушки быстрее чем непосредственно вдоль провода. Поэтому фазовая скорость волны относительно провода выше скорости света, причем в разы. Это не противоречит теории относительности. Достаточно упомянуть, что в полых волноводах фазовая скорость волны тоже выше скорости света. Для понимания этого кажущегося парадокса следует различать фазовую и групповую скорости электромагнитной волны. Для чего отсылаю к учебникам…
Катушка с одним заземленным концом резонирует на частотах nλ0/4, где n – целое число, λ0 – длина волны рабочей частоты и fsrf = vax/λ0. Поэтому увеличение частоты собственного резонанса сводится к увеличению значения vax. Из-за наличия высших мод ЭМ-волны, частота первого резонанса катушки всегда выше частоты, рассчитанной исходя из длины провода. По этой же причине высшие по частоте резонансы не кратны первому и друг другу. При изменении шага намотки vax имеет максимум при шаге спирали примерно равном радиусу намотки (радиус a = D / 2). Однако катушки с большим шагом намотки (p ≈ a) не представляют практического интереса, поскольку имеют малую индуктивность. При увеличении шага намотки частота собственного резонанса катушки растет (при p < a), но рост этот идет за счет снижения величины индуктивности. При фиксированной индуктивности, если увеличивать шаг намотки, нам приходится добавлять витки и выигрыша мы практически не получаем.
У коротких катушек на каркасах большого диаметра последующие резонансы отстоят от первого далеко выше по частоте, что можно видеть по результатам HFSS моделирования: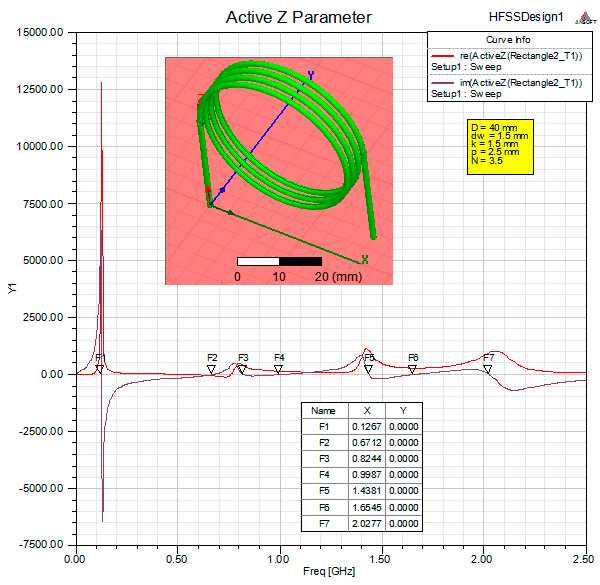 На частотах много ниже частоты первого резонанса пространственные задержки намного меньше периода колебаний, ЭМ-поле вокруг катушки представляет собой поле соленоида и скорость распространения волны вдоль ее оси можно не учитывать. В таком случае RLC-модель из сосредоточенных элементов будет вполне рабочей и достаточно точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это вовсе не статическая емкость между витками. В таком режиме работают катушки из всех наших трех моделей в КВ диапазоне и ниже. Однако уже на частоте первого резонанса начинают проявляться волновые эффекты, связанные с ограниченной скоростью передачи электромагнитных взаимодействий и катушку следует рассматривать только как спиральный волновод. В этом случае RLC модель не только не годится для расчетов, но и приводит к неверному пониманию самого механизма возникновения резонансных явлений в катушке. В этой связи хочется отметить наличие в Сети ложной идеи о том, что в катушке одновременно происходят как волновой резонанс, так и LC-резонанс на сосредоточенных индуктивности и пресловутой «межвитковой емкости». Такое утверждение равносильно тому, что в катушке имеются два механизма распространения электромагнитных взаимодействий. Один происходит, как обычно, со скоростью света и определяет волновой резонанс. Второй осуществляется мгновенно с бесконечной скоростью в виртуальных сосредоточенных элементах катушки. Ведь фазовый сдвиг между током и напряжением в реактивных элементах — это совсем не то пространственное запаздывание, о котором идет речь. На самом деле катушка, как набор сосредоточенных RLC элементов, и катушка, как цепь с распределенными параметрами — это две разные математические модели одной и той же реальной катушки. Первая модель не учитывает ограниченную скорость передачи взаимодействий, основана на предположении, что плотность тока во всех витках всегда одинакова, что не имеет место при собственном резонансе спирали. Поэтому эта модель ограничена и применима только на низких частотах. Вторая модель — более полная, учитывает то, что не учла первая и применима на любой частоте. В этом нет ничего необычного. Любая цепь, физические размеры которой сравнимы с длиной волны, не может рассматриваться как цепь из сосредоточенных элементов, в которой не учитывается ограниченная скорость передачи электромагнитных взаимодействий. Именно по этой причине О.Хевисайд и предложил в 1885 г. свою теорию длинных линий, а заодно кстати и само абстрактное математическое понятие “индуктивность”. Как положительную реактивность.
На частотах много ниже частоты первого резонанса пространственные задержки намного меньше периода колебаний, ЭМ-поле вокруг катушки представляет собой поле соленоида и скорость распространения волны вдоль ее оси можно не учитывать. В таком случае RLC-модель из сосредоточенных элементов будет вполне рабочей и достаточно точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это вовсе не статическая емкость между витками. В таком режиме работают катушки из всех наших трех моделей в КВ диапазоне и ниже. Однако уже на частоте первого резонанса начинают проявляться волновые эффекты, связанные с ограниченной скоростью передачи электромагнитных взаимодействий и катушку следует рассматривать только как спиральный волновод. В этом случае RLC модель не только не годится для расчетов, но и приводит к неверному пониманию самого механизма возникновения резонансных явлений в катушке. В этой связи хочется отметить наличие в Сети ложной идеи о том, что в катушке одновременно происходят как волновой резонанс, так и LC-резонанс на сосредоточенных индуктивности и пресловутой «межвитковой емкости». Такое утверждение равносильно тому, что в катушке имеются два механизма распространения электромагнитных взаимодействий. Один происходит, как обычно, со скоростью света и определяет волновой резонанс. Второй осуществляется мгновенно с бесконечной скоростью в виртуальных сосредоточенных элементах катушки. Ведь фазовый сдвиг между током и напряжением в реактивных элементах — это совсем не то пространственное запаздывание, о котором идет речь. На самом деле катушка, как набор сосредоточенных RLC элементов, и катушка, как цепь с распределенными параметрами — это две разные математические модели одной и той же реальной катушки. Первая модель не учитывает ограниченную скорость передачи взаимодействий, основана на предположении, что плотность тока во всех витках всегда одинакова, что не имеет место при собственном резонансе спирали. Поэтому эта модель ограничена и применима только на низких частотах. Вторая модель — более полная, учитывает то, что не учла первая и применима на любой частоте. В этом нет ничего необычного. Любая цепь, физические размеры которой сравнимы с длиной волны, не может рассматриваться как цепь из сосредоточенных элементов, в которой не учитывается ограниченная скорость передачи электромагнитных взаимодействий. Именно по этой причине О.Хевисайд и предложил в 1885 г. свою теорию длинных линий, а заодно кстати и само абстрактное математическое понятие “индуктивность”. Как положительную реактивность.
Особо хотелось бы отметить следующий момент. На низких частотах, где, как мы выяснили, RLC модель справедлива, можно считать, что как индуктивность так и собственная емкость катушки не зависят от частоты, а определяются только геометрией намотки. Это общеизвестный факт, который зафиксирован например в формуле Нагаока. Однако реально параметры спиральной длинной линии зависят от частоты. Не только vax, но и погонная емкость и погонная индуктивность и, как следствие – величины собственной индуктивности и собственной емкости катушки в целом. Только на низких частотах эта зависимость пренебрежимо мала, а вот уже на частотах близких к первому резонансу значения индуктивности и собственной емкости катушки начинают заметно “плыть” по частоте. В итоге, мы сталкиваемся с ситуацией, что эти значения, измеренные или рассчитанные на низкой частоте, не пригодны для расчета частоты собственного резонанса катушки как LC резонанса по формуле Томсона. Расчет даст неверный результат! Неверный, Карл! Таким образом, мы приходим к выводу, что расчеты, основанные на понятии о LC-резонансе в катушке, полностью теряют смысл, что еще раз доказывает несостоятельность RLC-модели катушки не только для объяснения физических явлений при собственном резонансе, но и для расчетов в этой частотной области. Поэтому приходится прибегать к более сложному численному методу из работы [5], включающему в себя функции Бесселя и прочий суровый матан, что и делает Coil32.
Как видно из HFSS-моделей, у катушки как первый резонанс так и все последующие связаны исключительно с волновыми явлениями в катушке. Возможны практические случаи, когда катушка работает в диапазоне частот, в который попадает не только ее первый резонанс, но и более высокие. Очень хорошо такой случай описан в статье И.Гончаренко об анодном дросселе коротковолнового передатчика [2]. На этом примере хорошо видно, что для правильного понимания механизма резонансных явлений в катушке необходимо пользоваться теорией длинных линий.
Кроме фазовой скорости волны в катушке на частоту собственного резонанса оказывает влияние так называемый торцевой эффект, подобный хорошо известному аналогичному понятию из теории антенн, от которого зависит коэффициент укорочения вибратора. Этот эффект проявляется от того, что ЭМ-поле вокруг катушки занимает пространство большее, чем сама катушка. Наличие торцевого эффекта понижает резонансную частоту и этот эффект более выражен у коротких катушек с большим диаметром, что еще раз подтверждает родственную связь резонансных явлений в катушке и в вибраторе. Учитывая фазовую скорость вдоль оси катушки и явление торцевого эффекта мы можем рассчитать частоту собственного резонанса катушки по следующей весьма приближенной формуле от G3RBJ:
| [3] |
где:
- fsrf – частота собственного резонанса [МГц]
- ĺw – длина провода катушки с учетом торцевого эффекта [м]
- lw – реальная длина провода катушки [м]
- D, p, l – диаметр, шаг и длина намотки, соответственно [м]
- 0,25 – коэффициент, определяющий четвертьволновый резонанс (для полуволнового – 0,5)
Если конструктору необходимо создать катушку, имеющую минимальные габариты и максимальную частоту собственного резонанса при заданной индуктивности, то наиболее оптимальна будет намотка с расстоянием между витками, равном диаметру провода, при отношении l/D ≈ 1..1,5. Хотелось бы обратить внимание конструкторов, что здесь идет речь о вычислении собственной резонансной частоты “голой катушки в вакууме”, т.е. одной проволочной спирали без учета влияния каркаса, сердечника, экрана, изоляции провода и т.п. Все эти, трудно поддаваемые учету факторы, приводят к уменьшению этой частоты. Причем влияние оказывает все — любой проводник, печатная плата, корпус конструкции. В наших HFSS-моделях влияющие факторы — это выводы спирали и, особенно, сплошная земля в 1-ой и 3-ей моделях. Даже если вы соберетесь измерить частоту собственного резонанса экспериментально, это будет непростой задачей, так как щупы измерительного оборудования также оказывают влияние, даже если катушка где то висит в воздухе!
Необходимо отметить, что строгого аналитического решения уравнений Максвелла для цилиндрической проволочной спирали не существует, поэтому в теории спиральный волновод представляют в виде эквивалентной модели из тонкостенного сплошного цилиндра с анизотропной проводимостью. Однако численные методы решения уравнений Максвелла (чем в принципе и занимается HFSS) приводят нас к вполне однозначным результатам. В итоге, следует иметь ввиду, что вышеприведенная простая аналитическая формула [3] является весьма приблизительной и не может быть применима к любой катушке с произвольной геометрией намотки. Поэтому в Coil32 расчет частоты собственного резонанса основан не на аналитическом, а на численном методе из работы [5], который проверен практическими измерениями. При этом не учитывается влияние экрана, каркаса и других факторов. Расчет имеет точность около 10% при 0,04 < l/D < 40. Для некоторых катушек, например для очень длинных соленоидов с большим числом витков, этот метод может давать неверный результат. На практике же следует придерживаться следующего простого условия: если длина провода, которым намотана катушка, меньше четверти длины волны на наивысшей рабочей частоте, то катушка будет работать ниже своего первого резонанса.
P.S: В заключении хотелось бы добавить несколько слов о концепции “Двух независимых резонансов в катушке – волновом и LC-резонансе”. Эта концепция зиждется на трех ложных в своей основе предпосылках и поэтому в корне неверна:
- Любую линейную замкнутую электрическую цепь можно представить как набор из сосредоточенных RLC-элементов. Основными законами этой цепи являются законы Ома и Кирхгофа. Любое изменение топологии цепи или добавление элементов в нее полностью меняет распределение токов и напряжений во всей цепи. Однако в концепции “двойного резонанса” длинная линия считается этаким себе “черным ящиком”, равноценным какому-то особому четвертому сосредоточенному элементу, волновые процессы внутри которого существуют сами по себе. Но не стоит забывать, что другое название длинной линии – линия с распределенными параметрами, когда она представляется как цепь из бесконечного числа RLC-элементов. В ней также справедливы те же самые законы Ома и Кирхгофа, только представленные уже в дифференциальной форме. Мы просто перешли на более высокий уровень математической абстракции, при котором учитываются пространственно-временные задержки сигнала, но сути дела это не меняет. Поэтому, если мы подключим параллельно такой линии сосредоточенную емкость и будем считать, что характер распределения токов и напряжений внутри самой линии не изменится, мы просто отрицаем сами законы Ома и Кирхгофа. При этом не надо забывать, что характер распространения ЭМ-волны в линии и характер распределения токов и напряжений в ней – вещи жестко взаимосвязанные. Вывод – волновые процессы в линии не являются каким то особым ее свойством, которое существует само по себе, независимо от общих законов электрических цепей. Эти законы настолько фундаментальны, что в определенной мере отображены на еще более высоком уровне математической абстракции в уравнениях Максвелла, которые описывают свойства самой электромагнитной волны.
- “При сворачивании линии в спираль мало что меняется”. Это утверждение неверно. По крайней мере индуктивность значительно увеличивается, иначе зачем сворачивать? Кроме того, погонная емкость и погонная индуктивность такой линии уже становятся зависимыми от частоты. В результате, как отмечалось выше, формула Томсона для расчета частоты собственного резонанса в спиральной линии перестает работать.
- В итоге, на основе этих неверных предпосылок, утверждается наличие двух независимых резонансов и нам выкатывают две формулы. Формулу Томсона, которая на самом деле в этом случае не работает, и формулу от Alane Payne (G3RBJ), которая, как мы отметили выше, является сильно приближенной. И по этим двум формулам уже идет развитие “теории двух независимых резонансов”, которых в реальности не существует, что подтверждают и расчеты в HFSS и точные измерения. Повторюсь еще раз – все дело в разных математических моделях одной реальной катушки и разных уровнях математических абстракций в зависимости от конкретных условий расчета. Смешивать все это в одну кучу и подгонять под выдуманную теорию нельзя.
Ссылки по теме:
- Техническая электродинамика, Семенов Н.А., Изд. “Связь” Москва, 1973, стр.318-323.
- Моделирование анодного дросселя как распределенной структуры – И.Гончаренко 2007-2012
- Паразитные резонансы в катушке П-контура – И.Гончаренко
- Высокочастотные катушки, спиральные резонаторы и увеличение напряжения из-за когерентных пространственных мод 2001г. (Оригинал статьи здесь)
- THE SELF-RESONANCE AND SELF-CAPACITANCE OF SOLENOID COILS – applicable theory, models and calculation methods. By David W Knight (G3YNH)
- The self-resonance and self-capacitance of solenoid coils by David W Knight – основная статья с массой полезных ссылок по теме, в том числе на экспериментальные исследования с наглядными фото (G3YNH)
- SELF-RESONANCE IN COILS and the self-capacitance myth. By Alane Payne (G3RBJ)
- О собственной емкости катушки.
coil32.ru


