Расчет катушки индуктивности: Расчет катушки индуктивности | Онлайн калькулятор

Содержание

Расчет катушки индуктивности онлайн калькулятор

Чтобы Вы хотели? * – Выберите -Установка ж/б опорПодключение объекта к электроснабжениюЭлектромонтажные работыИспытание электроустановокПроектные работыПрочее

Тип подключения – Выбирите -Частный жилой домАдминистративное зданиеПроизводственное предприятиеМногоквартирный жилой домПрочее

Тип работ Внутренние сети 0,4 кВВнешние кабельные линии 0,4 кВВнешние кабельные линии 6/10 кВВоздушные линии 0,4 кВВоздушные линии 6/10 кВМонтаж трансформаторной подстанцииПодключение оборудованияВосстановление поврежденных КЛ или ВЛЗамена существующей электропроводкиИскусственное освещениеКомплексные работыСлаботочные сети и СКС

Тип испытаний Комплексные испытания 0,4 кВСопротивление изоляцииМеталлосвязьПетля фаза нольИспытание УЗОИспытание кабельных линийИспытание КТП и РПИспытание силовых трансформаторовПрочее

Тип работ Внешние электросистемыВнутренние электросистемыСлаботочные сетиИскусственное освещениеКомплексные работыПрочее

Населенный пункт

Км от Рязани В городе или до 10 кмдо 20 кмдо 30 кмСвыше 30 км

Количество опор 12345678

Обвязка под провод СИП (анкерное или промежуточное крепление) НетДа

Подъезд только на внедорожной технике НетДа

Тип опоры CB95-2CB110

Тип подключения 15 кВт5 кВт

Наличие технических условий НетДа

Наличие проектной документации НетДа

Проводились ли аналогичные испытания до этого НетДа

Желаемая дата начала работ

Сроки производства работ

Добавить документы Комментарий

         __        __      _  __        __      _   _     
_ __   \ \      / /     | | \ \      / /     | | | |    
| '_ \   \ \ /\ / /   _  | |  \ \ /\ / /   _  | | | |    
| |_) |   \ V  V /   | |_| |   \ V  V /   | |_| | | |___ 
| . __/     \_/\_/     \___/     \_/\_/     \___/  |_____|
 |_|

Введите код с изображенния *

Расчёт катушки индуктивности под динамик

Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.

На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.

высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.

Пример расчета

Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.

е. умножить на 1000.

Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.

откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
диаметр жилы: d =0,84h / √ω
= 0,84 х 26,96 / √ 135,36 = 1,95 мм;
масса намотки: m = (h³ х 10^-3) / 21,4 = (26,96³ х 10^-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.

Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.

Итак имеем данные, которые понадобятся для расчета будущей катушки:

высота намотки h = 26,96 мм;
значит внутренний диаметр a = 53,92 мм;
соответственно внешний: b = 107,84 мм;
длинна жилы: 34,3 м;
количество витков: 135;
диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).

Статья специально подготовлена для сайта ldsound.ru

Расчет катушек индуктивности в 3D с помощью COMSOL Multiphysics

При проектировании индукционных устройств важно учитывать различные электродинамические эффекты. Модуль AC/DC пакета COMSOL Multiphysics предоставляет все необходимые инструменты для эффективного и простого моделирования и проектирования катушек индуктивности, а также для расчёта их сосредоточенных характеристик в соответствии с заданными требованиями.

Базовые принципы работы катушки индуктивности

Простейшая катушка индуктивности — это электрический провод (обмотка или катушка), намотанный вокруг магнитного материала (

магнитопровода). Принцип действия катушки основывается на принципе индуктивности, вокруг устройства наводится магнитное поле, которое препятствует изменению тока, текущего по проводнику.

Простейшая катушка индуктивности, состоящая из медной обмотки и железного сердечника. Красными стрелками показано направление тока, а синими — магнитное поле вокруг сердечника. Изменение тока приводит к изменению магнитного потока через обмотку, что создаёт разность потенциалов в обмотке, которая препятствует изменению тока.

Индуктивность — это параметр, который обозначается буквой L и показывает, в какой степени происходит сопротивление протеканию тока, он является ключевой характеристикой идеального индуктора. К сожалению, в нашем мире нет идеальных вещей и в реальных катушках индуктивности наблюдаются резистивные эффекты, которые больше проявляются на низких частотах и характеризуются активным сопротивлением (R), и ёмкостные эффекты, которые наблюдаются на высоких частотах и характеризуются ёмкостью (C), приводащие в т.

ч. авторезонансным процессам. На самом деле, принцип действия катушки индуктивности можно понять, рассмотрев простейшую RLC-цепь.

Эквивалентная схема катушки индуктивности.

С помощью набора пассивных элементов, можно собрать схему замещения, которая будет полностью соответствовать и описывать свойства индуктивности в различных приложениях. К примеру, если через катушку индуктивности протекает переменный ток, то она является низкочастотным фильтром, а последовательно соединённая с конденсатором – резонансным или полосовым фильтром. Катушки индуктивности играют очень важную роль в современном мире и повседневной жизни. Они используются в различных импульсных источниках питания и согласующих схемах, подключаемых к радиочастотным антеннам. Умный светофор, который загорается зелёным при вашем приближении, может быть индуктивным датчиком, который упрощает вашу жизнь в пути.

Оптимизация катушки индуктивности

Если в вашем устройстве присутствует катушка индуктивности, то важно знать некоторые её характеристики, чтобы полностью понимать, как работает устройство в целом. Ключевыми параметрами являются – индуктивность, активное сопротивление, электрическая ёмкость, резонансная частота и добротность (Q-factor), то есть ширина области резонанса. Эти параметры определяют частоту среза или полосу пропускания фильтра, либо просто реактивное сопротивление согласующей схемы.

Другой потенциально важной задачей при использовании катушек индуктивности является учет электромагнитных помех (ЭМП) или электромагнитной совместимости (ЭМС). Вокруг катушек индуктивности создаётся магнитное поле. При проектировании необходимо точно знать, насколько оно будет влиять на другие компоненты и близлежащие устройства. Это особенно актуально при нынешней миниатюризации всех устройств.

На данный момент существуют только грубые аналитические и эмпирические формулы, описывающие эти RLC параметры. С их помощью нельзя точно спроектировать современное устройство. Аналитические формулы в основном пригодны только для расчёта элементарных трёхмерных форм, например, куба, цилиндра, спирали и тора. Однако с помощью них невозможно рассчитать форму и поведение магнитного поля вокруг индуктивного устройства для ЭМП/ЭМС (EMI/EMC) исследований.

Дополнительно, часто требуется изготовление магнитопровода из нелинейного материала для увеличения индуктивности и ограничения окружающего магнитного поля. Это очевидно еще больше усложняет расчёты и приводит к очередной аналитической или эмпирической аппроксимации, что негативно сказывается на результате. Для получения точных рабочих характеристик трёхмерного индукционного устройства, численное моделирование является более надёжным и корректным решением.

3D-моделирование катушки индуктивности в COMSOL Multiphysics

COMSOL Multiphysics предлагает пользователю все необходимые инструменты для получения полных рабочих характеристик катушки индуктивности. Давайте рассмотрим данный функционал программы на учебном примере Modeling of a 3D Inductor (Моделирование катушки индуктивности в 3D). Он доступен в Application Gallery (Галерее моделей и приложений) для модуля AC/DC. Он как раз служит для наглядной иллюстрации процесса проектирования катушки индуктивности и расчета ее рабочих характеристик.

Геометрия катушки индуктивности для конечно-элементной модели.

В реальных устройствах протекающий через катушку ток можно задавать разными способами. Например, приложением напряжения, тока или мощности. Это может быть либо постоянная, либо периодическая величина, или какая-нибудь сложная функция, зависящая от времени. В нашем примере для задания тока используются условия

Coil с опцией Single Turn (Одиночный проводник) и Lumped Port (Сосредоточенный порт) для низких и высоких частот соответственно. Таким образом, вы можете управлять катушками.

На видео продемонстрирована последовательность шагов по моделированию трёхмерной катушки индуктивности в COMSOL Multiphysics.

COMSOL Multiphysics позволяет легко добавлять в модель электрические сосредоточенные компоненты и цепи, которые можно как создать в самой программе, так и импортировать, как список SPICE. Благодаря мультифизическим связкам можно подключать данные цепи к распределенным устройствам, котороме моделируются методом конечных элементов. Всё это можно делать с помощью встроенных функций взаимосвязи. К примеру, вы можете подключить вашу катушки индуктивности к цепи управления, приложив минимум усилий. Программа сама находит те части, которые вы можете связать, и предлагает вам выбрать нужные из выпадающего списка.

При выборе нужной опции из выпадающего списка терминал катушки индуктивности (показан синим цветом) автоматически связывается с электрической цепью.

На высоких частотах (на которых может работать ваша катушка индуктивности) в проводниках с током в следствие скин-эффекта ток вытесняется к поверхности. В данном примере мы можем учесть данный эффект с помощью использования граничного условия Impedance boundary condition (Импедансное граничное условие). Решение задачи растекания тока в тонких слоях — это очень ресурсоёмкая задача. Но переходя к упрощенному описанию проводника с помощью граничного условия мы упрощаем данную задачу и значительно экономим время расчёта.

На рисунке изображён график распределения плотности тока (Am^-2) в катушке на высокой частоте. Обратите внимание, что учитывается неравномерное протекание тока.

Добротность катушки индуктивности во многом зависит от свойств материала магнитопровода, в частности от потерь. Возможности COMSOL Multiphysics позволяют отредактировать любой материал из библиотеки, чтобы добавить или заменить необходимые свойства. Любые потери на вихревые токи автоматически учитываются в расчёте. В данном примере диэлектрические потери в магнитопроводе задаются пользователем с помощью добавления мнимой части к диэлектрической постоянной, ε_r. Таким же образом вы можете добавить магнитные потери в вашу модель, задав комплексное значение магнитной проницаемости μ_r.

Постобработка и анализ результатов расчёта модели индуктора

Если вам необходимо произвести впечатление на клиентов или завоевать их доверие, буквально в несколько кликов вы можете создать красивейшие графики, благодаря встроенным возможностям постобработки результатов в COMSOL Multiphysics. Программное обеспечение автоматически вычисляет и предоставляет вам доступ к переменным, которые в полной мере характеризуют работу вашей спроектированной катушки индуктивности — магнитное поле, токи и величина потерь. В учебном примере трёхмерной катушки индуктивности продемонстрировано, как настроить детализированной изоражение ниже.

Чем тоньше магнитопровод, тем больше в нём магнитная индукция на поверхности (Тл). В катушке также показано распределение потенциала (В).

Для лучшей наглядности вы можете добавить другие типы трёхмерных графиков, например, Streamline (Силовые линии) или Arrow (Векторная диаграмма).

Магнитная индукция на поверхности магнитопровода (Тл). Силовые линии плотности тока (Aмм^-2) в катушке показывают более высокую плотность в закруглённых частях. Красными стрелками показано магнитное поле.

Наконец, для получения полных характеристик катушки индуктивности вам необходимо определиеть значения импеданса и резонансных частот. Одна из переменных в COMSOL Multiphysics автоматически рассчитывает точный импеданс для каждой частоты. Таким образом, графики данных величин можно построить очень легко. Используя встроенные операторы real (действительная часть) и imag (мнимая часть), можно строить графики активного (резистивного) и реактивного (индуктивного/ёмкостного) импеданса, на которых легко увидеть резонанс.

Действительная (слева) и мнимая (справа) части импеданса (Z) показывают резонанс и переключение между индуктивным и ёмкостным поведением.

На графике мнимой части можно также заметить, что после прохождения через резонансную частоту знак изменяется с положительного на отрицательный. Это значит, что на высоких частотах устройство больше проявляет ёмкостный характер, чем индуктивный, что вполне ожидаемо.

Учёт термических эффекто в модели катушки индуктивности

COMSOL Multiphysics специально проектировался, чтобы пользователям было легко связывать различные физические интерфейсы в одной модели. Как раз поэтому второе слово в названии — «multiphysics». Дальнейшим расширением модели может являться добавление и учет электромагнитного нагрева. Протекающие в катушке токи, вихревые токи и диэлектрические/магнитные потери в магнитопроводе, все они приводят к выделению тепла, которое распространяется по проводящим металлическим компонентам с высокой теплопроводностью и, отчасти, нагревает окружающие устройства и платы. Используя физический интерфейс Induction Heating (Индукционный нагрев), вы запросто сможете рассчитать интенсивность теплопередачи и распределение температур в индукционных устройствах.

Узнайте больше о моделировании индукционных устройств в COMSOL Multiphysics

Ознакомьтесь с другими учебными моделями катушек индуктивности в галерее моделей и приложений:
Посмотрите, как используют COMSOL Multiphysics для проектирования индукционных устройств:

Конструкторский расчет катушки индуктивности (стр. 1 из 4)

ВВЕДЕНИЕ

Катушка индуктивности является элементом радиоэлектронных средств функционирование которой определяется эффектом перехода энергии электрического поля в энергию магнитного поля вследствие протекания по контуру катушки электрического тока. Величина индуктивности определяется конструкцией токопровода и его размерами.

Различают катушки постоянной и переменной индуктивности. Катушки с большими изменениями индуктивности являются вариометрами, а с малыми изменениями индуктивности (10-15%) – подстроенными.

По конструктивному исполнению катушки делятся на цилиндрические и плоские. Цилиндрические катушки индуктивности бывают каркасные и бескаркасные.

Различают катушки индуктивности с однослойной и многослойной намоткой. Многослойные катушки менее технологичны и менее надежны. Различают также экранированные и неэкранированные катушки индуктивности.

В катушках индуктивности применяют магнитные и немагнитные сердечники характер, которого влияет на добротность катушки и интервал варьирования величины индуктивности.

Возможности создания миниатюрных катушек индуктивности очень малы.

В катушках индуктивности потери, влияющие на добротность, складываются из потерь элементов конструкции и увеличиваются при уменьшении размеров конструкции.

В производстве интегральных схем наметилась тенденция замены катушек индуктивности специальными схемами на транзисторах. В производстве гибридно-пленочных интегральных схем катушку индуктивности выполняют в планарном исполнении.

Перспектива развития катушек индуктивности связаны с разработкой новых материалов, имеющие высокие магнитные проницаемости и стабильность на радиочастотах, превосходящие по своим свойствам ферриты, а также развитием конструкции и технологии изготовления таких изделий.

1. АНАЛИЗ ТЕХНИЧЕСКОГО ЗАДАНИЯ

Заданная величина индуктивности, равная 2 мкГн, подстройка величины индуктивности ±5% от указанного значения, интервал варьирования лежит от 1,65 мкГн до 2,35 мкГн, может быть выполнена однослойной намоткой на каркас, в качестве которого может служить немагнитный сердечник, изменяя положение немагнитного сердечника относительно намотки можно достичь указанных пределов изменения индуктивности.

Рабочая частота 29 МГц.

Для эксплуатации необходимо, максимальную надежность конструкции, жесткость, защиту от влияния внешних воздействий: механических и электромагнитных, также необходимо ограничить влияние на другие элементы магнитного поля данной катушки. Кроме этого необходимо обеспечить минимальные габариты изделия.

Для обеспечения годовой программы выпуска, равной 1000 штук, необходимо как можно большая технологичность, а именно количество операций по сборке катушки индуктивности должно быть минимальным.

Годовой выпуск разрабатываемого изделия ориентировано на выпуск 1000 изделий в год, что при количестве рабочих дней 250 в году и односменной работе на участке сборки составляет 4 изделий за рабочую смену.

Условия эксплуатации – следует принять общеклиматическую группу с наибольшим разбросом температур, а именно: О 2.1 по ГОСТ 15150-69.Для того чтобы индуктивность катушки не выходила за указанный интервал, необходимо чтобы температурный коэффициент индуктивности был минимален, это значит, что необходимо использовать материалы с малыми значениями температурного коэффициента линейного расширения.

В задание были поставлены довольно строгие требования к параметрам катушки индуктивности так, область использования катушки требует от нее малой массы и габаритов; программа выпуска требует максимальной технологичности и простоты конструкции; при этом необходимо обеспечить максимальную добротность катушки.

2. ОБЗОР АНАЛОГИЧНЫХ КОНСТРУКЦИЙ

В источнике [1, стр. 164] приведены конструкции типичных катушек индуктивности в миниатюризированном исполнении, эскиз такой конструкции приведен на рисунке 2.1.

1 – экран;

2- прокладка;

3- продстроечник;

4- каркас;

5- обмотка;

6- кольцо;

7- основание.

Рисунок 2.1 – Эскиз миниатюрного исполнения катушки индуктивности (диаметром 9 мм).

Для обеспечения заданной величины индуктивности намотку достаточно выполнить однослойной и с шагом, что облегчит сборку конструкции и уменьшит паразитную емкость.

Величина индуктивности таких катушек колеблется в пределах от сотых долей до сотен микрогенри. Должна обеспечиваться точность в пределах 0,3…0,5%. На практике применяются катушки индуктивности цилиндрические и кольцевые. Для обеспечения высокой добротности в качестве каркаса используются керамики. В настоящее время применяются катушки индуктивности с каркасами из вакуумплтной керамики. Для уменьшения ТКИ и потерь в собственной емкости каркасы имеют ребристую поверхность. Материалом для каркасов служит керамика. Используются каркасы диаметром от 4…30 мм.

Катушки на керамических каркасах изготавливают тремя способами:

на каркас наматывают с натяжением медный провод;

на горячий каркас наматывают с натяжением медную ленту;

на каркас наносят воженное серебро в виде витков обмотки и покрывают их гальвано способом слоем меди.

Для устранения паразитных связей, обусловленных внешним электромагнитным полем катушки, и для устранения влияния окружающего пространства катушка экранируется, т.е. располагается внутри замкнутого металлического заземлённого экрана.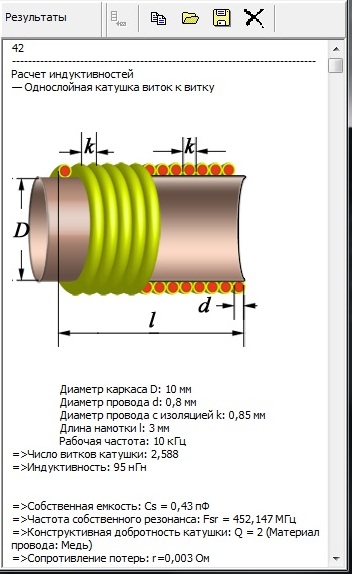 На практике материал для экрана используется из алюминиевого сплава. Под влиянием алюминиевого экрана уменьшается её индуктивность, увеличивается сопротивление и собственная ёмкость, но это приводит к снижению температурной стабильности индуктивности.

Практически величина добротности находится в пределах 10…1000, лучшая добротность однослойных цилиндрических катушек достигается при

. Величина добротности зависит от частоты, геометрических размеров и конструкции, числа витков и типа провода. Так, на частотах до 3…4 МГц преимущественно следует использовать провод типа литцендрат (ЛЭШО, ЛЭЛО, ЛЭВ, ЛЭТ), так как это позволяет получить более высокую добротность. При более высоких частотах применяют одножильный провод (ПЭВ, ПЭМ, ПЭЛО, ПЭЛ)

Добротность катушек на кольцевых каркасах относительно меньше, чем у таких же катушек на цилиндрических каркасах.

3. ЭЛЕКТРИЧЕСКИЙ И КОНСТРУКТОРСКИЙ РАСЧЕТ КАТУШКИ ИНДУКТИВНОСТИ

3.1 Выбор материала и обоснование конструкции

Материал, из которого изготовлена обмотка катушки индуктивности, должен обладать низким удельным сопротивлением во избежание влияния на протекающий электрический ток, и сравнительно не большой коэффициент линейного расширения – этим требованиям вполне удовлетворяют серебро и медь.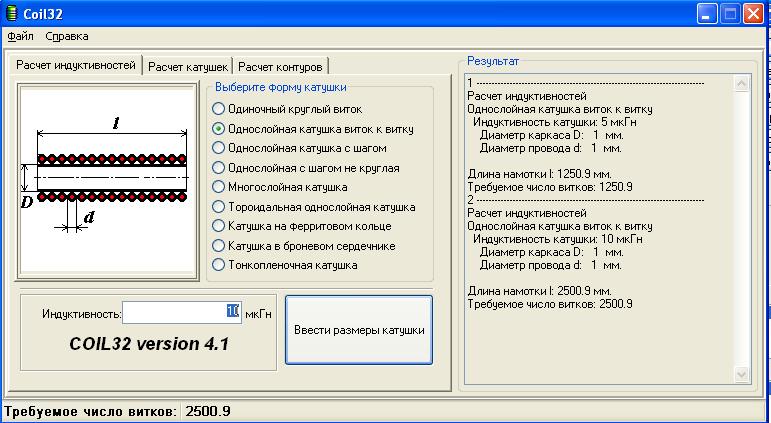 Для большей доступности этот материал должен иметь не высокую стоимость. Наиболее всего этим требованиям удовлетворяет медь имея:

; .

Намотку осуществим обычным проводом круглого диаметра. Примем к расчету следующий провод: ПЭЛ-0,5 ГОСТ 16186 – 74.

В качестве материала каркаса используем керамику для уменьшения потерь в диэлектрике каркаса и увеличения добротности. Для уменьшения собственной емкости, но достижения высокой добротности используем каркас диаметром 10 мм.

Для подстройки индуктивности катушек КВ и УКВ часто применяются немагнитные сердечники из меди или латуни . Проанализировав рабочие частоты мы примем немагнитный сердечник выполненный из меди .Это приведет к уменьшению индуктивности и понизит ее добротность .

Для упрощения расчёта сопротивления проводника переменному току вводят понятие “глубина проникновения тока”, под которой понимают некоторую величину слоя x_э , на протяжении которой плотность тока уменьшается до 0,37 от его значения на поверхности проводника. Величину проникновения тока определяют по формуле (3.1)

, где (3.1)

r –удельное сопротивление материала проводника, 0,017Ом.мм²/м;

f– частота тока. МГц.

Тогда конструкция экрана будет представлять достаточно прочную конструкцию с высокой проводимостью. В принципе для обеспечения большей жесткости экрана было бы лучше изготовить из материалов с высокой прочностью (большей, чем прочность бронзы, латуни), но это будет связано с дополнительными технологически операциями и затруднит обработку. Толщина стенок экрана на практике не превышает 2 мм.

Примем толщину стенок – 0,5 мм.

Диаметр экрана примем равный 8мм, тогда диаметр внутренней поверхности составит 7 мм.

Длину экрана примем равной 12мм.

Тип намотки выбирается сплошным с шагом – для уменьшения длины намотки и свести габариты к минимуму. Данный тип намотки выбран как наиболее простой, а значит для условий массового производства, наиболее подходящим.

Конструктивные элементы катушки (каркас, кольцо, прокладка и т.д. ) – должны обладать высоким омическим сопротивлением, высокой диэлектрической проницаемостью (малым тангенсом угла диэлектрических потерь) и слабой зависимостью диэлектрической проницаемости от частоты и температуры, малый коэффициент линейного расширения. Из курса материаловедения известно, что к таким материалам относятся: керамики, стекла и фторопласт. Для повышения технологичности необходимо использовать материал, выполняющий из керамики у которого e =4÷6;

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.

Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников.

Расчет однослойных цилиндрических катушек производится по формуле

где L — индуктивность катушки, мкГн; D — диаметр катушки, см; l — длина намотки катушки, см; n—число витков катушки.

При расчете катушки могут встретиться два случая:

а) по заданным геометрическим размерам необходимо определить индуктивность катушки;

б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 97; для этого подставим в формулу все необходимые величины:

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и

длину намотки, а затем рассчитывают число витков по формуле

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле

где d— диаметр провода, мм, l — длина обмотки, мм, п — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины,

получим:

Диаметр провода

Если эту катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки. Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки. Возможно, также придется увеличить и то и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным выше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше половины диаметра D/2 , то более точные результаты можно получить по формулам

В.Г.Бастанов, “300 практических советов”

Катушки индуктивности | Онлайн журнал электрика

Катушки индуктивности позволяют припасать электронную энергию в магнитном поле. Обычными областями их внедрения являются сглаживающие фильтры и разные селективные цепи.

Электронные свойства катушек индуктивности определяются их конструкцией, качествами материала магнитопровода и его конфигурацией, числом витков обмотки.

Ниже приведены главные причины, которые следует учесть при выборе катушки индуктивности:

а) требуемое значение индуктивности (Гн, мГн, мкГн, нГн),

б) наибольший ток катушки. Большой ток очень небезопасен из-за очень сильного нагрева, при котором повреждается изоляция обмоток. Не считая того, при очень большенном токе может произойти насыщение магнитопровода магнитным потоком, что приведет к значительному уменьшению индуктивности,

в) точность выполнения индуктивности,

г) температурный коэффициент индуктивности,

д) стабильность, определяемая зависимостью индуктивности от наружных причин,

е) активное сопротивление провода обмотки,

ж) добротность катушки. Она обычно определяется на рабочей частоте как отношение индуктивною и активного сопротивлений,

з) частотный спектр катушки.

В текущее время выпускаются радиочастотные катушки индуктивности на фиксированые значения частоты с индуктивностями от 1 мкГн до 10 мГн. Для подстройки резонансных контуров лучше иметь катушки с регулируемой индуктивностью.

Однослойные с незамкнутым магнитопроводом катушки индуктивности используются в цепях опции устройств.

Мультислойные с не замкнутым магнитопроводом катушки употребляются в фильтрах и высокочастотных трансформаторах. Мультислойные катушки индуктивности броневого типа с сердечником из феррита используются в фильтрах низких и средних частот и трансформаторах, а подобные катушки, но со железным сердечником употребляются в сглаживающих дросселях и низкочастотных фильтрах.

Формулы для расчета катушки индуктивности

Главные аппроксимирующие соотношения, применяемые при проектировании катушек индуктивности, имеют последующий вид.

1. Характеристики однослойных катушек индуктивности у каких отношение длины к поперечнику больше 5, определяются в виде

где L — индуктивность, мкГн, М- число витков, d — поперечник катушки, см, l — длина намотки, см.

2. Характеристики мультислойных катушек индуктивности, у каких отношение поперечника к длине больше 1, определяются в виде

где L — индуктивность, мкГн, N — число витков, dм — средний поперечник обмотки, см, d — толщина обмотки, см.

Одно- и мультислойные катушки с незамкнутым ферритовым магнитопроводом будут иметь индуктивность в 1,5 — 3 раза больше зависимо от параметров и конфигурации сердечника. Латунный сердечник, вставленный заместо ферритового. уменьшит индуктивность до 60-90% по сопоставлению с ее значением без сердечника.

Для сокращения числа витков при сохранении той же индуктивности можно использовать ферритовый сердечник.

При изготовлении катушек индуктивностью от 100 мкГн до 100 мГн для областей низких и средних частот целенаправлено применить чашечные ферритовые броневые сердечники серии КМ. Магнитопровод в данном случае состоит из 2-ух подогнанных друг к другу чашек, к которым прилагаются односекционная катушка, две крепежные клипсы и подстроечный стержень.

Нужная индуктивность и число витков могут быть вычислены по формулам

где N — число витков, L — индуктивность, нГн, Аl — коэффициент индуктивности, нГн/вит.

Всегда необходимо держать в голове о том, что до этого, чем рассчитывать индуктивность, следует найти число витков, которые могут поместиться на данной катушке.

Чем меньше поперечник провода, тем больше число витков, но тем больше сопротивление провода и, естественно, его нагрев из-за выделяющейся мощности, равной I²R. Действующее значение тока катушки не должно превосходить 100 мА для провода поперечником 0,2 мм. 750 мА — для 0,5 мм и 4 А — для 1 мм.

Маленькие замечания и советы

Индуктивность катушек со железным сердечником очень стремительно миниатюризируется с ростом неизменной составляющей тока обмотки. Это необходимо подразумевать в особенности при проектировании сглаживающих фильтров источников электропитания.

Наибольший ток катушки индуктивности находится в зависимости от температуры окружающей среда, при этом он отдал жен уменьшаться с ее повышением. Потому для обеспечения надежной работы устройства следует обеспечить большой припас по току.

Ферритовые тороидальные сердечники эффективны для производства фильтров и трансформаторов на частотах выше 30 МГц. При всем этом обмотки состоят всего только из нескольких витков.

При использовании всех типов сердечников часть магнитных силовых линий замыкается не по магнитопроводу, а через окружающее его место. В особенности очень этот эффект проявляется в случае незамкнутых магнитопроводов. Заметим, что эти магнитные поля рассеяния являются источниками помех, потому в аппаратуре сердечники необходимо располагать так, чтоб по способности уменьшить эти помехи.

Катушки индуктивности имеют определенную паразитную емкость, которая образует колебательный контур в купе с индуктивностью катушки. Резонансная частота такового контура для различных типов катушек индуктивности может варьироваться в границах от 20 кГц до 100 МГц.

Школа для электрика

Расчет катушки индуктивности колебательного контура и обоснование выбора материалов.

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ

АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ

имени академика С. П. Королёва ( СГАУ )

Факультет инженеров воздушного транспорта

Кафедра электронных систем и устройств

Выполнил студентка: Воробьёва А.Ю.

Группа № 3203

Вариант № 33

Проверил преподаватель:

Макарычев Ю.И.

Самара 2011

Содержание

1 Задание для расчета	3
2 Расчет	3
2. 1 Нахождение индуктивности L_к	3
2.2 Выбор материала каркаса	4
2.3 Выбор размеров каркаса	4
2.4 Расчет индуктивности катушки с учетом сердечника.	5
2.5 Определение числа витков	6
2.6 Определение оптимального диаметра провода	7
2.7 Учет влияния экрана	9
2.8 Расчет собственной емкости катушки.	10
2.9 Расчет добротности	11
3 Расчет ТКИ и ТКЧ	12
4 Выбор конденсатора контура	13
5 Итог	15
Список используемой литературы	16

1 Задание.

Рассчитать индуктивность колебательного контура на резонансной частоте .При условии, что емкость конденсатора . Тип и материалы сердечников, , и другие необходимые данные для расчета приведены

Материал экрана: алюминий.

Тип и материал сердечника: СЦР-1,Р-20.

Выбрать материал и размеры каркаса, тип намотки. Определить число витков и оптимальный диаметр провода. Вычислить собственную емкость, добротность, температурный коэффициент индуктивности и температурный коэффициент частоты.

Рисунок 1.Колебательный контур.

где С_к– емкость контура;

L_к– индуктивность контура.

2 Расчет

2.1 Нахождение индуктивности контура.

Рисунок 2. Схема замещения катушки идеальными элементами.

где L – идеальная индуктивность катушки;

С₀– собственная емкость катушки;

r_f– сопротивление обмотки катушки;

r_д– сопротивление диэлектрика каркаса за счет поляризации.

Определим индуктивность исходя из формулы

определим L.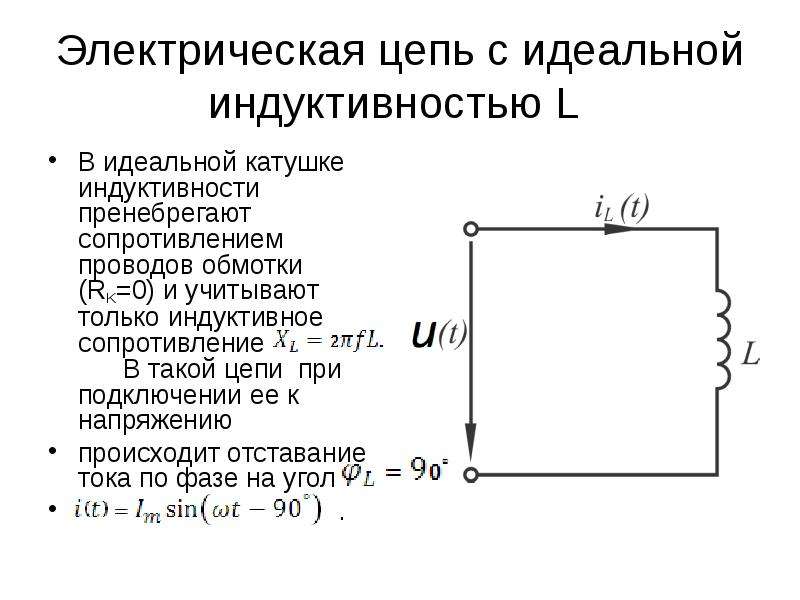

2.2 Выбор материала каркаса.

Каркас катушки в значительной степени определяет ее стоимость и электрические параметры.

Каркас должен быть удобным для намотки и крепления в приборе, обеспечивать устройство (распайку) выводов обмотки и надежную фиксацию положения построечного элемента. Материал каркаса должен допускать применение прогрессивных технологических методов изготовления, быть дешевым, механически прочным, вносить малые потери, обладать необходимой теплостойкостью, малой влагостойкостью и небольшим коэффициентом линейного расширения и, в ряде случаев, малым значением температурного коэффициента диэлектрической проницаемости.

В достаточной степени этим требованиям отвечают каркасы из полистирола, фенопластов, пресс-материалов типов АГ-4С, ДСВ-2Р-2М и им подобных. На пониженных частотах может оказаться целесообразным применение более дешевых каркасов из бакелизированных трубок.

Для каркасов катушек с высокой стабильностью применяют радиокерамику типа В, радиофарфор, ультрафарфор и высокочастотный стеатитит.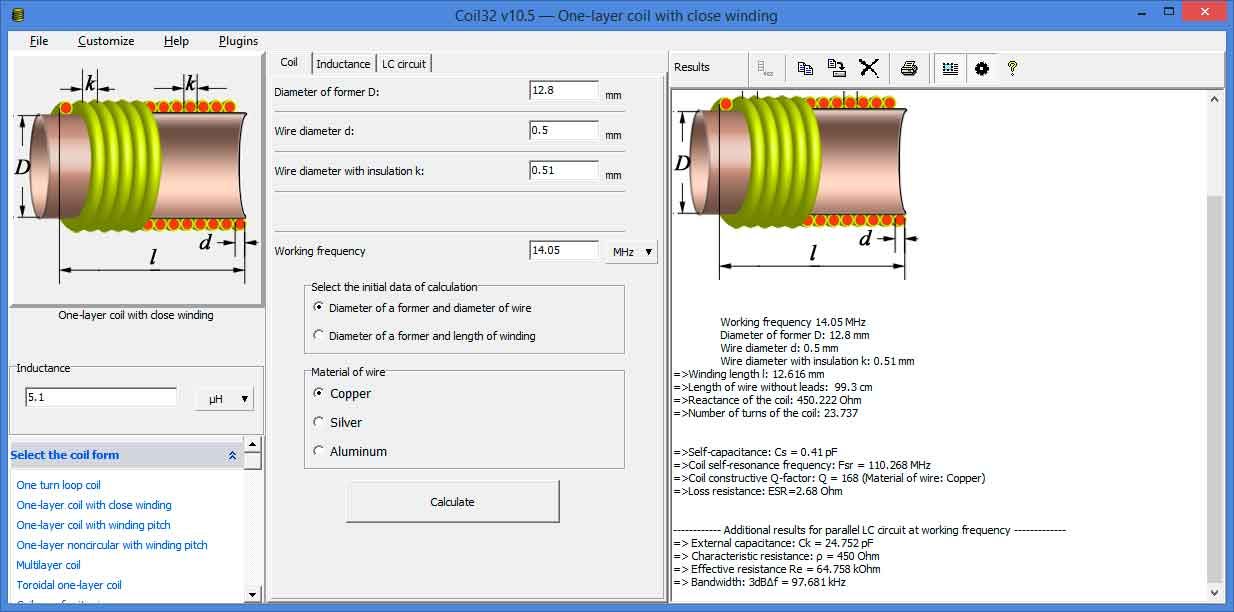

Исходя из заданных параметров наиболее подходящим материалом является

высокочастотный стеатитит.

2.3 Выбор размеров каркаса.

Прежде чем приступить к дальнейшим вычислениям, для удобства, приведем чертеж катушки:

Рисунок 3. Чертеж катушки индуктивности.

где l_c – длина сердечника;

l_к – длина намотки;

D_c – диаметр сердечника;

D_к – диаметр катушки;

d – диаметр провода без изоляции.

По сводным таблицам для СЦР – 1 можно найти D_c=0,6см, l_c=0,9см.

Для цилиндрических сердечников D_k=0,9см и предварительно возьмем l_к=0,9см.

2.4 Расчет индуктивности катушки с учетом сердечника.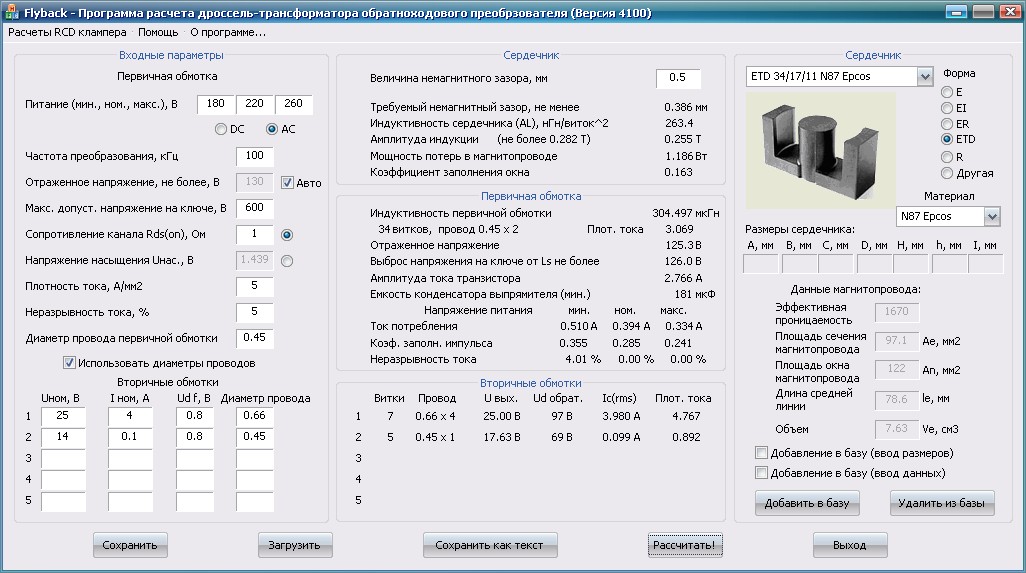

где – необходимая величина расчетной индуктивности;

– действующая магнитная проницаемость сердечника.

где – начальная магнитная проницаемость материала сердечника;

– коэффициент использования магнитных свойств;

-поправочный коэффициент.

определяем по графику =f(l_k/ D_c), определяем по графику =f(l_c/ D_c)

(l_k/ D_c)=0,9/0,6=1,5; =0,28.

(l_c/ D_c)=0,9/0,6=1,5; =0,9.

определяем по таблице, исходя из того, что задана марка магнитного материала Р-20.

=10.

Таким образом

2.5 Определение числа витков и типа намотки.

Применяемые виды намотки можно разделить на однослойные и многослойные.

При однослойной намотке витки располагаются на цилиндрической поверхности каркаса в один слой. При плотном расположении витков, разделяемых лишь изоляцией провода, получается сплошная однослойная намотка при расположении витков на некотором расстоянии друг от друга — намотка с шагом.

Однослойные катушки с шагом отличаются высокой добротностью (150 -400) и стабильностью; они в основном применяются в контурах KB и УКВ.

Для повышения точности намотки провода применяются нарезные каркасы, т. е. каркасы, на поверхности которых сделана неглубокая (0,2 — 0,3d) спиральная канавка. Однако погружение провода в диэлектрик каркаса несколько понижает добротность и стабильность катушки.

Для высокостабильных катушек применяются специальные способы изготовления намоток – тугая, горячая и осажденная или нанесенная намотки.

Катушки без каркаса могут быть практически выполнены при числе витков не более трех.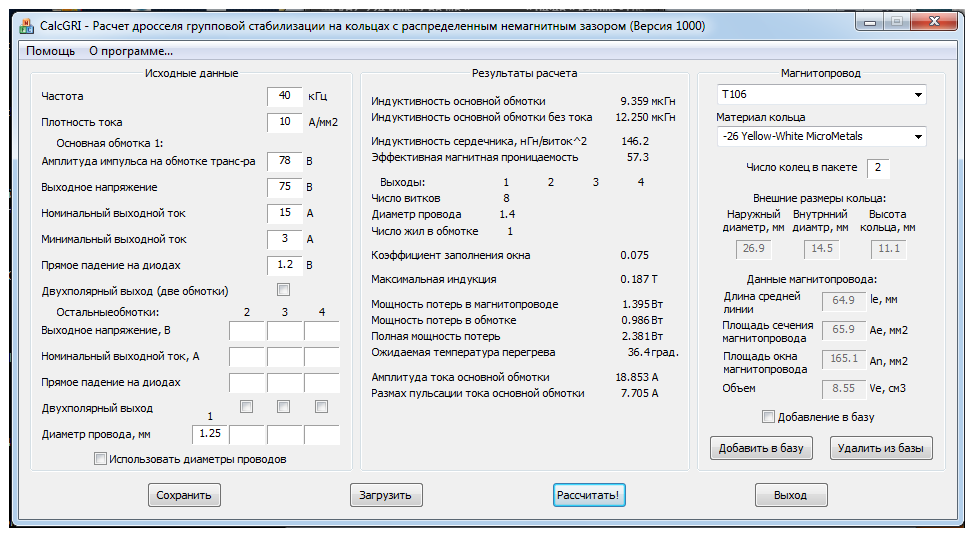 Они отличаются несколько более высокой добротностью, но, имеют малую механическую жесткость и пониженную стабильность.

Для катушек индуктивностью выше 15—20 мкГн применяют сплошную однослойную намотку. Целесообразность перехода на сплошную намотку определяется диаметром катушки: чем больше диаметр катушки, тем большая индуктивность может быть получена при применении намотки с шагом.

Катушки со сплошной намоткой также отличаются высокой добротностью (150—250) и стабильностью и широко используются в контурах для коротких, промежуточных и средних волн, если требуется индуктивность не выше 200—500 мкГн.

Для изготовления катушек с индуктивностью выше 200—500 мкГн применяют многослойные намотки.

Целесообразность перехода на многослойную намотку определяется диаметром катушки. Чем больше диаметр катушки, тем при большей индуктивности следует переходить на многослойную намотку.

Многослойные намотки могут быть разделены на простые и сложные.

Широкое применение имеют сложные многослойные намотки, например универсальные.

Катушки, предназначенные для работы в диапазоне частот до 500 кГц, имеют многослойную обмотку. Применяют рядовую многослойную или универсальную намотки, а также намотку «внавал». Катушки для частот выше 1—2 МГц имеют однослойную намотку.

Для намотки катушек применяют провода в эмалевой изоляции марок ПЭЛ, ПЭ, ПЭВ, комбинированной изоляции марок ПШО, ПШД, ПЭЛШО, ПЭШД, а также литцендрат ЛЭШО И ЛЭШД.

Для многослойных катушек с универсальной намоткой применяют обычно провода с волокнистой изоляцией, так как волокнистая изоляция обеспечивает большее сцепление витков.

Для катушек с шагом применяется неизолированный провод МГМ, покрытый слоем серебра.

В данной работе целесообразно применить однослойную намотку из ПЭЛ.

Для определения числа витков однослойной катушки воспользуемся формулой:

Значение L₀ определяем по графику, L₀=f(l_k/ D_к)

(l_k/ D_к)=1; L₀ =7

Откуда

2. 6 Определение оптимального диаметра провода.

Между сопротивлением провода катушки и его диаметром существует сложная зависимость, так как при этом изменяется проявление поверхностного эффекта и эффекта близости.

Рассмотрим вопрос о влиянии диаметра провода на сопротивление катушки. В случае прямолинейного провода увеличение диаметра вызывает увеличение его периметра, а, следовательно, уменьшение сопротивления току высокой частоты. Зависимость сопротивления отрезка прямолинейного провода от диаметра при некоторой частоте выражается кривой L на рис. 4 (кривая I представляет собой зависимость сопротивления току высокой частоты от диаметра). При свертывании провода в спираль возникает эффект близости, который проявляется тем сильнее, чем больше диаметр провода. Увеличение сопротивления за счет эффекта близости примерно пропорционально диаметру провода и изображается прямой II. Сложив величины, характеризуемые кривыми I и II, получим изменение полного активного сопротивления провода катушки в зависимости от его диаметра; эта зависимость выражается кривой III. Ход кривой III показывает, что при вполне определенном диаметре провода сопротивление катушки имеет минимальное значение. Можно показать, что при этом сопротивление провода катушки (с учетом поверхностного эффекта) равно увеличению сопротивления за счет эффекта близости.

Рис. 4

Оптимальный диаметр провода катушки рассчитывают при помощи вспомогательного коэффициента:

где – вспомогательный параметр;

-поправочный коэффициент.

D_к – диаметр катушки;

N –число витков намотки;

где f ₀– резонансная частота.

к=f(l/D)

к=4

,т.к. , то ;

0,065см, в целях экономии меди возьмем d_опт = 0,69мм

Используя эмалевую изоляцию провода типа ПЭЛ принимаем диаметр провода равным 0,35

Проведем проверку подобранного диаметра провода:

, следовательно, выбор параметров каркаса сделан правильно.

2.7 Учет влияния экрана.

Для устранения паразитных связей, обусловленных внешним электромагнитным полем катушки, и для устранения влияния внешних полей катушка экранируется, то есть располагается внутри замкнутого, металлического заземленного экрана.

Экранирующее действие характеризуется отношением напряженности внешнего поля катушки при наличии экрана к напряженности поля при его отсутствии. Для экрана среднего качества, выполненного, например, в виде алюминиевого стакана, это отношение равно приблизительно 0,01 — 0,05, что бывает достаточно для большинства практических случаев. Для усиления экранирующего действия применяются двойные и даже тройные экраны.

Под влиянием экрана изменяются основные электрические параметры катушки; уменьшается ее индуктивность, а также увеличиваются сопротивление и собственная емкость. Добротность экранированной катушки оказывается ниже добротности той же катушки при отсутствии экрана. Изменение параметров катушки зависит от соотношения между ее размерами и размерами экрана.

Для того чтобы индуктивность и добротность падали не более чем на 10%:, рекомендуются следующие соотношения м.д. диаметрами экрана и катушки:[3]

;

где – диаметр экрана.

Выберем диаметр экрана равным 2,3см, высоту равную 1,8см;

При помещении катушки в экран ее индуктивность и добротность уменьшаются. Индуктивность экранированной катушки составляет:

где – индуктивность неэкранированной катушки;

к – коэффициент связи м.д. экраном и катушкой.

Для однослойных катушек:

где – коэффициент зависящий от отношения длины катушки к ее диаметру.

;

Определяем индуктивность экранированной катушки:

Т. к и высота между катушкой и экраном равна высоте катушки, то потери вносимые экраном в К.И. можно определить по формуле:[3]

Где латуни

2.8 Расчет собственной емкости катушки.

В катушке, между отдельными витками и между витками и ближайшими металлическими телами—экранами, шасси прибора и т. п., всегда существует разность потенциалов, которая создает электрическое поле. Влияние этого поля подобно влиянию некоторой емкости, включенной параллельно катушке; эту емкость называют собственной (или распределенной) емкостью катушки. Ее величина зависит от размеров катушки, конструкции обмотки, близости расположения витков со значительной разностью потенциалов, удаленности их от экранов, диэлектрической проницаемости изоляции провода и каркаса, а также ряда других конструктивных факторов. Чем больше диаметр катушки, чем ближе друг к другу расположены витки со значительной разностью потенциалов, чем выше диэлектрическая проницаемость изоляции провода и материала каркаса, тем больше собственная емкость катушки индуктивности.

Наименьшей собственной емкостью (1—2 пФ) обладают однослойные катушки, намотанные с шагом. Многослойные катушки обладают большей емкостью,- величина которой зависит от способа намотки. Например, емкость катушек с простой универсальной намоткой составляет 5 — 10 пФ, с перекрестной универсальной намоткой 15 – 30 пФ.

Расчет собственной емкости однослойных катушек удобнее производить по эмпирической формуле:

где определяется по графикам.

Тогда

2.9 Расчет добротности.

Добротность контура зависит не только от его параметров, но также и от параметров внешней цепи — внутреннего сопротивления источника и сопротивления нагрузки.

Добротность контура определяют по формуле:

Сопротивление току высокой частоты.

Для катушек, работающих на частотах выше 10МГц, сопротивление вычисляется по формуле:

где d – диаметр провода без изоляции;

N – число витков катушки;

D – диаметр катушки;

Ом

Потери вносимые сердечником.

Потери вносимые сердечником могут быть найдены по следующей формуле:

Предположим, что катушка находится в радиоприемнике, тогда Н=0, и тогда

Ом.

Потери в диэлектрике.

Диэлектрические потери возникают в поле собственной емкости катушки через диэлектрик С_ол и зависят от величины этой емкости, качества tgδ материала каркаса и частоты. Потери в диэлектрике обусловлены тем, что между соседними витками катушки существует емкость, имеющая две составляющих — емкость через воздух С_ови емкость через диэлектрик С_ол.

рис.5

Сопротивление, вносимое диэлектрическими потерями, можно представить включенным параллельно собственной емкости катушки. Величина этого сопротивления равна:[3]

Пересчитывая это сопротивление на последовательное, получаем:

Откуда , поэтому добротность контура равна:

Индуктивность | Физика II

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность . Взаимная индуктивность – это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.

Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что « E ₂ индуцированная» представляет наведенную ЭДС в катушке 2. )

Во многих случаях, когда геометрия устройств является фиксированной, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока, Δ I / Δ t , как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как

[латекс] {\ text {emf}} _ {2} = – M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],

, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от Transformers. Единицами для M являются (В с) / A = Ом с, который назван генри (H) в честь Джозефа Генри. То есть 1 H = 1 Ω⋅s. Природа здесь симметрична.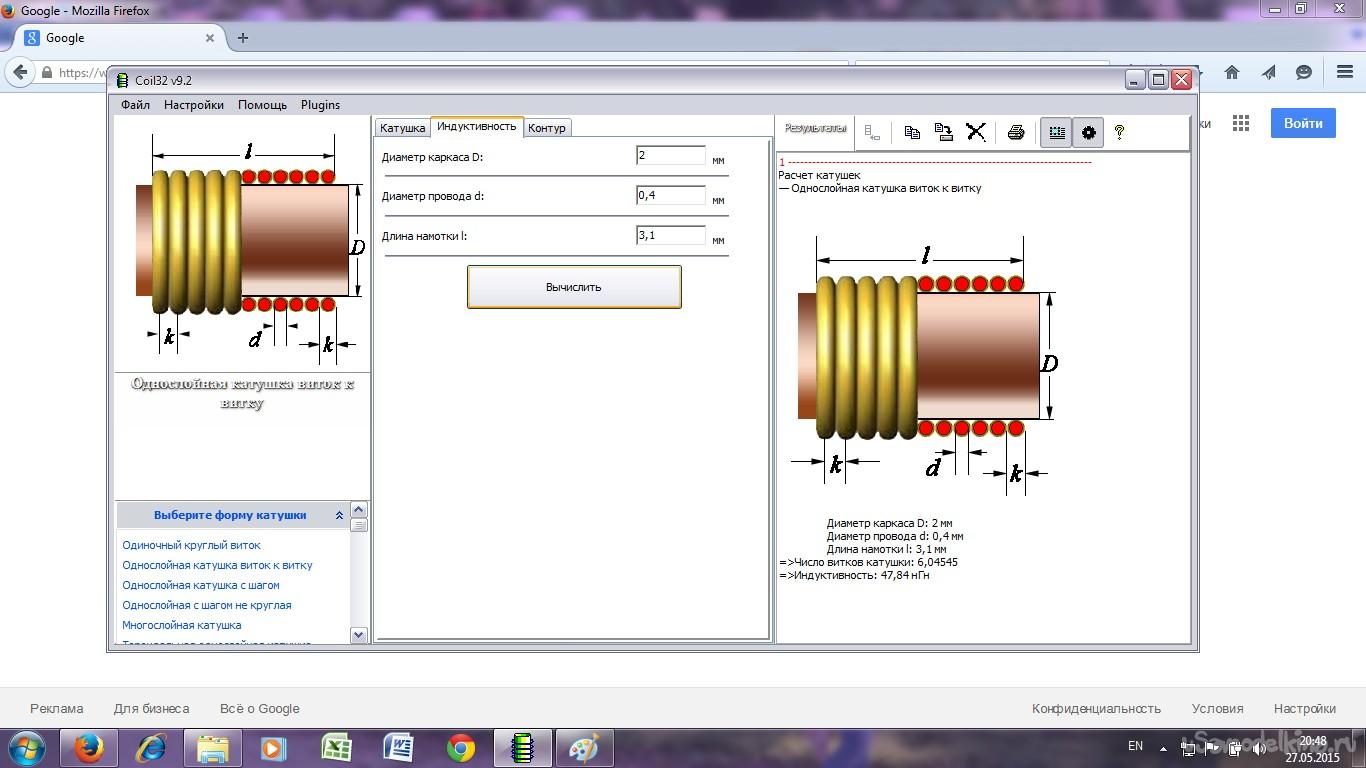 Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] {\ text {emf}} _ {1} = – M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],

, где M то же самое, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть, а может и не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(См. Рисунок 2.)

Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.

Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = – L \ frac {\ Delta I} {\ Delta t} [/ latex],

, где L – собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рисунок 3.

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2.Катушка индуктивности 1 H – это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = – L (Δ I / Δ t ), будет препятствовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = – L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Знак плюс означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению.Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока. Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт.(Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. Рисунок 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.

Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле.В большинстве случаев это сложно из-за сложности создаваемого поля. Таким образом, в этом тексте индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = – Н (Δ Φ / Δ t ) и, по определению самоиндукции, как ЭДС = – L . (Δ I / Δ т ).Приравнивая эти доходности к

[латекс] \ text {emf} = – N \ frac {\ Delta \ Phi} {\ Delta t} = – L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]

Решение для л дает

[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]

Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ латекс]. (Здесь n = N / , где N – количество катушек, а ℓ – длина соленоида.{2} A} {\ ell} \ text {(соленоид)} \\ [/ latex].

Это самоиндукция соленоида с площадью поперечного сечения A и длиной . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением. {2} \ влево (1.{2} \ right)} {0.100 \ text {m}} \\ & = & 0.632 \ text {mH} \ end {array} \\ [/ latex].

Обсуждение

Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.

Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)

Как избежать насыщения индуктора в конструкции источника питания | Статья

СТАТЬЯ

Получайте ценные ресурсы прямо на свой почтовый ящик – рассылается раз в месяц

Мы ценим вашу конфиденциальность

Катушка индуктивности – важный компонент источника постоянного / постоянного тока.При выборе индуктора следует учитывать множество факторов, таких как значение индуктивности, DCR, размер и ток насыщения. Режим насыщения катушки индуктивности часто неправильно понимается и может вызвать проблемы. В этой статье будет рассмотрено, как насыщаются катушки индуктивности, как насыщение влияет на схему, а также методы определения насыщения катушек индуктивности.

Причины насыщения индуктора

Чтобы понять, как индуктор насыщается, см. Рисунок 1 и шаги для насыщения индуктора, описанные ниже:

Когда ток проходит через катушку, показанную на Рисунке 1, катушка создает магнитное поле.
Магнитопровод намагничивается полем, и его внутренний магнитный домен медленно вращается.
Когда магнитопровод полностью намагничен, направление магнитных доменов согласовывается с магнитным полем. Даже если добавлено внешнее магнитное поле, сердечник не имеет вращающихся магнитных доменов. Это означает, что индуктор насыщен.

Рисунок 1: Диаграмма насыщения индуктора

На рис. 2 показан другой вид насыщения индуктора, а также уравнение, показывающее, как плотность потока системы (B) и напряженность магнитного поля (H) могут влиять на индуктивность.

Когда плотность магнитного потока достигает BM, плотность магнитного потока больше не увеличивается с увеличением напряженности магнитного поля. Это означает, что индуктор насыщен.

Рассмотрим взаимосвязь между индуктивностью и магнитной проницаемостью (µ). Когда индуктор насыщен, µ значительно уменьшается; поэтому индуктивность будет значительно уменьшена, и способность подавить ток будет потеряна.

Рисунок 2: Кривая намагничивания и формулы

Советы по оценке насыщения индуктора:

Существует две категории оценки насыщения индуктора в практических приложениях: теоретические расчеты и экспериментальные испытания. Рисунок 3 суммирует эти методы.

Рисунок 3: Методы определения насыщения индуктора

Теоретические расчеты требуют расчета максимальной плотности магнитного потока или максимального тока индуктора. С другой стороны, экспериментальные испытания в основном сосредоточены на форме волны тока катушки индуктивности и других методах предварительной оценки. Эти методы описаны более подробно ниже.

Метод 1. Расчет плотности магнитного потока

Метод 1 подходит для сценариев, в которых магнитные сердечники используются для проектирования индукторов.Например, параметры сердечника включают длину магнитного пути (lE) и эффективную площадь (AE). Тип магнитного сердечника также определяет соответствующую марку магнитного материала, и для магнитного материала требуются соответствующие правила в отношении потерь в сердечнике и плотности магнитного потока насыщения (см. Рисунок 4) .

Рисунок 4: Параметры и характеристики индуктора

С помощью этих материалов мы можем рассчитать максимальную плотность магнитного потока в соответствии с фактическим расчетным сценарием. На рисунке 5 показаны формулы для расчета максимальной плотности магнитного потока.

Рисунок 5: Формулы плотности магнитного потока

На практике расчет можно упростить, и вместо µR можно использовать µI. По сравнению с плотностью потока насыщения магнитного материала, можно определить, подвержена ли расчетная индуктивность риску насыщения.

Метод 2: Расчет максимального тока индуктора

Этот метод подходит для проектирования схем с непосредственным использованием существующих катушек индуктивности.Различные топологии схем имеют разные формулы для расчета тока индуктора.

Возьмем, к примеру, импульсный преобразователь MP2145. Ток катушки индуктивности можно рассчитать по формулам, приведенным ниже, и сравнить результат расчета со значением, указанным в спецификации катушки индуктивности, чтобы определить, будет ли катушка индуктивности насыщена (см. Рисунок 6) .

Рисунок 6: Расчет максимального тока индуктора с помощью MP2145

Метод 3. Определить, насыщен ли индуктор кривой тока индуктора

Этот метод является наиболее распространенным и практичным, доступным инженерам.

Используйте инструмент моделирования MPSmart с MP2145. Из формы волны моделирования мы знаем, что, когда индуктор не насыщен, ток индуктора представляет собой треугольную волну с определенным наклоном. Когда катушка индуктивности насыщена, форма волны тока катушки индуктивности имеет значительные искажения, которые вызваны уменьшением степени насыщения (см. Рисунок 7).

Рисунок 7: Форма кривой тока индуктора для MP2145

Мы можем наблюдать искажение формы волны тока индуктора, чтобы определить, когда он становится насыщенным.

На рисунке 8 показана форма сигнала, измеренная на оценочной плате MP2145. После насыщения катушки индуктивности наблюдается очевидное искажение, что согласуется с результатами моделирования.

Рисунок 8: Форма сигнала оценочной платы MP2145

Метод 4: Измерьте аномальное повышение температуры индуктора и прислушайтесь к звукам

Если вы не знаете модель сердечника системы, может быть сложно определить ток насыщения катушки индуктивности. Иногда неудобно проверять ток индуктора, так как может потребоваться частичное снятие индуктора с печатной платы, чтобы измерить его ток.Еще одна хитрость – это измерение температуры индуктора с помощью тепловизора. Если температура значительно превышает расчетные, это может указывать на насыщение индуктора (см. Рисунок 9). Если вы поднесете ухо к индуктору и обнаружите, что он издает звуки, это также может указывать на его насыщение.

Рисунок 9: Измерение температуры индуктора с помощью тепловизора

При разработке источников питания с индукторами важно избегать насыщения индуктора.В этой статье объясняются некоторые из физических свойств, вызывающих насыщение магнетиков, и приводятся уравнения для выбора правильного значения индуктивности для вашей цепи, объемные изображения того, как выглядят формы волны тока, когда индукторы становятся насыщенными, а также другие уловки для наблюдения за насыщением индукторов. в вашем приложении. Чтобы выбрать индуктор для вашего следующего дизайн-проекта, см. Наш новый каталог индукторов.

_________________________

Вам это показалось интересным? Получайте ценные ресурсы прямо на свой почтовый ящик – рассылайте их раз в месяц!

Калькулятор импеданса индуктора

• Калькуляторы электрического, радиочастотного и электронного оборудования • Онлайн-преобразователи единиц измерения

Обратите внимание, что величина импеданса идеального индуктора равна его реактивному сопротивлению.Однако они не идентичны из-за сдвига фаз между напряжением и током в индуктивной цепи. Для расчета используется следующая формула:

где:

X _L – реактивное сопротивление катушки индуктивности в Ом (Ом),

Z _L – полное сопротивление катушки индуктивности в Ом (Ом). ),

ω = 2πf – угловая частота в рад / с,

f – частота в герцах (Гц),

L – индуктивность в генри (H) и

j – мнимая единица.

Для расчета введите индуктивность и частоту, выберите единицы измерения, и результат будет показан в омах.

Катушка индуктивности – это пассивный электрический компонент с двумя выводами, состоящий в основном из изолированного провода, намотанного на магнитопровод или без него (воздушный сердечник) в виде катушки. Катушки индуктивности еще называют катушками и дросселями. Магнитопровод обычно изготавливается из ферромагнитного металла, например железа или ферромагнитной керамики (феррита), и используется для увеличения магнитного поля и, таким образом, для увеличения индуктивности катушки.Как и конденсаторы, индукторы используются для хранения энергии. Однако, в отличие от конденсаторов, энергия в катушках индуктивности накапливается в магнитном поле, окружающем катушку индуктивности. Одно из применений катушек индуктивности – фильтры, используемые для устранения пульсаций на выходе постоянного тока или для предотвращения передачи радиочастотных (РЧ) помех через кабели. Индукторы широко используются в настраиваемых схемах радиопередатчиков и приемников, а также в трансформаторах.

Катушка индуктивности с воздушным сердечником и высокой добротностью в радиопередатчике

В отличие от конденсаторов, которые противодействуют скорости изменения напряжения на своих пластинах, индукторы противостоят скорости изменения тока , протекающего через них.В отличие от конденсаторов, которые не пропускают постоянный ток, индукторы легко пропускают его через себя. Индукторы сопротивляются только переменному току или изменяющемуся току, и эта способность сопротивляться току прямо пропорциональна их врожденному свойству, называемому индуктивностью, которая обозначается символом L в честь русского физика Эмиля Ленца и измеряется в генри, названной в честь американского ученого Джозефа Генри.

В отличие от резисторов, которые просто противодействуют прохождению электрического тока через них, создавая напряжение, прямо пропорциональное току, индукторы препятствуют изменениям тока , протекающего через них.Они создают падение напряжения, прямо пропорциональное скорости изменения тока через них . Полярность этого индуцированного напряжения всегда такова, что напряжение пытается поддерживать изменяющийся ток в его текущем состоянии. Например, когда ток увеличивается, напряжение имеет тенденцию противодействовать этому увеличению и поддерживать меньший ток, а когда ток уменьшается, напряжение имеет тенденцию противодействовать этому уменьшению и поддерживать более высокий ток. Более высокие скорости изменения тока всегда вызывают большее обратное напряжение.Из-за этого свойства это напряжение называется «обратной электродвижущей силой» («противо-ЭДС»). Чтобы отличить это свойство катушек от сопротивления, оно называется реактивным сопротивлением . Если на катушку подается синусоидальное напряжение, более высокие скорости изменения происходят на более высокой частоте, поэтому на более высоких частотах катушка становится более устойчивой к току, и ее реактивное сопротивление также увеличивается, как показано на графике.

График идеального реактивного сопротивления катушки индуктивности X _L и тока, протекающего через катушку индуктивности I в зависимости от частоты f для данной индуктивности, показывает прямую пропорциональность частоты для реактивного сопротивления и обратную пропорциональность для тока

Как и реактивное сопротивление, импеданс Z также измеряется в омах (Ом) и состоит из двух составляющих – действительной и мнимой части.Первый – это сопротивление R, которое замедляет ток из-за материала, который плохо проводит электричество, и его формы. Второй компонент – это реактивное сопротивление X, о котором говорилось выше, которое замедляет ток из-за противодействия электрического и магнитного полей.

Если реальная катушка индуктивности подключена к источнику постоянного тока , постоянный постоянный ток течет через катушку индуктивности, и он ограничивается только низким сопротивлением провода, из которого она сделана. Когда катушка индуктивности подключена к источнику постоянного напряжения постоянного тока, ток будет течь через катушку и медленно повышаться до своего максимального значения, которое определяется внутренним сопротивлением источника питания и внутренним сопротивлением витков катушки.Самоиндуцированная ЭДС на катушке индуктивности предотвращает быстрое увеличение тока и «борется» с приложенным напряжением, пока ток не достигнет своего максимального значения.

Если источник постоянного тока отсоединен от индуктора, ток, протекающий через него, будет постоянно падать до нуля, и снова обратная ЭДС индуктора будет «бороться» с изменением тока и будет пытаться сохранить ток неизменным. Со временем ток постепенно упадет до нуля.

В чисто индуктивной цепи ток отстает от напряжения на π /2 или 90 °.1 – ток имеет отрицательный максимум, скорость его изменения равна нулю, а напряжение равно нулю; 2 – ток равен нулю, скорость его изменения максимальная, а напряжение положительное максимальное; 3 – ток имеет положительный максимум, скорость его изменения равна нулю, а напряжение равно нулю; 4 – ток равен нулю, его скорость изменения максимальна, а напряжение равно отрицательному максимуму

Если переменное синусоидальное напряжение приложено к катушке, ток будет отставать от напряжения на некоторый фазовый угол, как показано на картинке.Для чистого индуктора этот фазовый угол будет составлять 90 ° или цикла. В точке на оси времени ( ωt = π /2), в которой ток равен нулю, на катушке индуктивности имеется положительное максимальное напряжение. По прошествии времени ток постепенно увеличивается, и вокруг катушки также нарастает магнитное поле. В этом магнитном поле индуцируется ЭДС, противодействующая току. Эта ЭДС является реакцией на изменение проходящего через него тока, и она максимальна, когда ток равен нулю, потому что в этот момент скорость изменения тока максимальна.Когда ток находится на пике (положительном или отрицательном), скорость изменения синусоидального тока равна нулю, и в этих точках обратная ЭДС также равна нулю. Это приводит к тому, что волна напряжения на 90 ° или π /2 не совпадает по фазе с волной тока. То есть напряжение опережает ток или ток отстает от напряжения.

Рассмотрим аналогию: Солнце (солнечный свет – напряжение) наиболее мощно в астрономический полдень, но самая жаркая часть дня (температура – ток) обычно наступает на несколько часов позже.Или зимнее солнцестояние в северном полушарии (самый короткий день) приходится на конец декабря, но самые холодные месяцы еще впереди – в зависимости от того, где вы живете, это январь или даже февраль. Причина этого «сезонного запаздывания» или «фазового сдвига» заключается в поглощении энергии Солнца массивными океанами Земли. Позже они отпускают его медленно – точно так же, как это делают индуктивности.

Зимнее солнцестояние в северном полушарии (самый короткий день) приходится на конец декабря, но самые холодные месяцы еще впереди – так ведет себя ток в катушке индуктивности

Расчетное сопротивление является мерой индуктивности. сопротивление сигналу на определенной частоте , который проходит через него.Индуктивное реактивное сопротивление изменяется с изменением частоты приложенного переменного напряжения. Формула и график выше показывают, что реактивное сопротивление катушки индуктивности X _L велико на высоких частотах и мало на низких частотах (конденсаторы ведут себя противоположным образом). На высокой частоте индуктивное сопротивление становится очень большим или полностью противоположным току. Индуктор блокирует ток высокой частоты. С другой стороны, при очень низких частотах или постоянном напряжении индуктор проводит очень хорошо – отсюда правило, которое мы усвоили в средней школе: индукторы блокируют переменный ток и пропускают постоянный ток.Если частота очень низкая, индукторы очень хорошо пропускают сигналы. Вот почему в кроссоверы вставляют катушки индуктивности, чтобы блокировать высокие частоты от драйверов сабвуфера.

Импеданс измеряется в омах, как и сопротивление. Так же, как сопротивление, импеданс показывает величину сопротивления индуктора потоку электрического тока. Но чем импеданс отличается от простого сопротивления? Разница заключается в зависимости импеданса от частоты сигнала. Сопротивление не зависит от частоты, а полное сопротивление катушек индуктивности зависит от нее.Импеданс катушек индуктивности уменьшается с увеличением частоты.

Этот калькулятор разработан для идеальных катушек индуктивности. Настоящие катушки индуктивности всегда имеют некоторое сопротивление последовательно с индуктивностью. Используйте наш калькулятор импеданса RL для расчета импеданса реальных катушек индуктивности.

Катушки индуктивности в ВЧ-модуле телевизионного приемника

Эта статья написана Анатолием Золотковым

Руководство по выбору индукторов для импульсных регуляторов

Чтобы просмотреть PDF-версию этой статьи, нажмите здесь.

Во всех импульсных регуляторах индуктивность используется как накопитель энергии. Когда полупроводниковый переключатель включен, ток в катушке индуктивности нарастает, и энергия накапливается. Когда переключатель выключается, эта энергия переходит в нагрузку. Количество сохраненной энергии определяется как Энергия = ½L.I ² (Джоули)

Где L – индуктивность в Генри, а I – пиковое значение тока катушки индуктивности.

Величина, на которую изменяется ток в катушке индуктивности во время цикла переключения, называется током пульсаций и определяется следующим уравнением:

В _л = Л.di / dt

Где V _l – напряжение на катушке индуктивности, di – ток пульсаций, а dt – продолжительность приложения напряжения. Из этого мы можем видеть, что значение тока пульсаций зависит от значения индуктивности.

Выбор индуктора

При выборе катушки индуктивности для понижающего преобразователя, как и для всех импульсных стабилизаторов, вам необходимо определить или рассчитать следующие параметры:

Максимальное входное напряжение
Выходное напряжение
Частота переключения
Максимальный пульсирующий ток
Продолжительность включения

Для понижающего преобразователя, показанного на Рис.2 , например, предположим, что частота переключения составляет 200 кГц, диапазон входного напряжения составляет 3,3 В ± 0,3 В, а выходное напряжение 1,8 В при 1,5 А при минимальной нагрузке 300 мА.

Для входного напряжения 3,6 В рабочий цикл будет:

D = V _o / V _i = 3,6 / 1,8 = 0,5

Где V _или – выходное напряжение, а V _i – входное напряжение.

Напряжение на индуктивности:

В _л = В _и – В _или = 1.8В при включенном переключателе;

В _l = – В _o = -1,8 В, когда переключатель выключен.

При выборе тока пульсаций 600 мА требуемая индуктивность составляет: L = В _l .dt / di = (1,8 × 0,5 / 200 × 10 ³) / 0,6

L = 7,5 мкГн

Для обеспечения некоторого запаса следует выбрать значение 10 мкГн. Это дает номинальный ток пульсаций от пика до пика 450 мА. В готовой конструкции это можно увидеть как пульсации выходного напряжения 0,45 × ESR выходного конденсатора.

Номинальный ток индуктора

Катушки индуктивности

обычно имеют два номинальных тока: непрерывный (Irms) и пиковый (Isat). Irms обычно определяется как постоянный ток, который вызывает повышение температуры индуктора на 40 ° C. Isat – это пиковый ток, который вызывает определенный спад индуктивности, определяемый как уменьшение в процентах от значения разомкнутой цепи и может варьироваться от 5% до 50%. Эти номинальные значения тока являются ориентировочными для характеристик катушки индуктивности. Фактический максимальный рабочий ток будет зависеть от области применения.Имея это в виду, необходимо проверить ряд факторов, чтобы гарантировать правильный выбор индуктора.

Во-первых, важно посмотреть, как индуктивность «спадает» с увеличением тока. Для таких материалов, как порошок железа, порошок пермаллоя молибдена (MPP), сендуст и аморфный порошок, в которых используется распределенный воздушный зазор, спад индуктивности начинается при очень низких уровнях тока и продолжается почти линейно по мере увеличения тока. Если используется ферритовый материал, любое постепенное изменение индуктивности компенсируется большим зазором, который необходимо ввести для хранения энергии.В результате индуктивность резко падает в точке, где весь сердечник становится насыщенным. До достижения этой точки индуктивность остается почти постоянной. Вы можете найти примеры этих двух характеристик спада в Рис. 3 . На этом рисунке показаны кривые спада для двух катушек индуктивности 920 мкГн – один изготовлен из феррита, а другой – MPP.

Для материалов с ферритовым сердечником пиковый ток обычно указывается для уменьшения индуктивности на 10–30% от значения разомкнутой цепи.Не рекомендуется работать при более высоких уровнях тока, так как индуктивность быстро упадет до низкого уровня. Однако для порошкообразных материалов пиковый ток может быть задан при любом спаде до 50% при работе за пределами этого диапазона при условии, что индуктор не перегревается. Из примеров в рис. 3 , пиковые токи будут определены от 16 до 17 А для ферритовой части и до 36 А для MMP.

Потери в сердечнике и температура

Допустимые потери для индуктора ограничены максимально допустимой температурой.Таким образом, для большинства стандартных деталей этот предел составляет 125 ° C, хотя он может быть и выше. Номинальный среднеквадратичный ток обычно представляет собой постоянный ток, который приводит к повышению температуры на 40 ° C, что теоретически допускает работу при температуре окружающей среды 85 ° C. Однако в большинстве приложений существует некоторая пульсация тока, возникающая из-за потерь в сердечнике. В таких условиях необходимо будет снизить номинальные параметры Irms, чтобы удерживать повышение температуры до 40 ° C. Кроме того, указанное повышение температуры на 40 ° C обычно достигается без ограничений в потоке воздуха из-за естественной конвекции, что в большинстве случаев не выполняется.

Двумя основными проблемами в этой области выбора индуктора являются расчет потерь в сердечнике и требуемое снижение номинальных значений Irms, чтобы удерживать повышение температуры до приемлемого уровня. У разных производителей катушек индуктивности есть разные способы выражения потерь в сердечнике – некоторые не приводят никаких подробностей, а другие предоставляют информацию, необходимую для расчета рассеяния. Однако один из наиболее практичных подходов исходит из каталога Coiltronics ^®, который показывает максимально допустимые потери в процентах от Irms по отношению к приложенным вольт-секундам на различных частотах.Поскольку произведение вольт-секунд пропорционально потерям в сердечнике, его можно легко определить с помощью этих кривых.

Окончательный отбор

Окончательный выбор индуктора зависит от четырех основных требований к конструкции: эффективности, электромагнитных помех (EMI), доступного пространства и стоимости. В портативном оборудовании с батарейным питанием требуется высокая эффективность от минимально возможной детали. Кроме того, поскольку электроника плотно упакована, низкий уровень электромагнитных помех очень важен. В промышленном применении, где основной источник постоянного тока генерируется от электросети переменного тока, эффективность становится менее важной.В результате часто используется самое дешевое решение.

Используя предыдущий пример понижающего преобразователя, вы можете теперь рассмотреть три возможных решения, предлагающих различные компромиссы с четырьмя конструктивными соображениями (, таблица 1, ).

Прежде чем сравнивать характеристики каждой из этих частей с критериями проектирования, вы должны сначала взглянуть на их характеристику спада. В нашем примере номинальный пиковый ток составлял 1,725 А (выходной ток 1,5 А плюс половина тока пульсаций), а максимальный пиковый ток составлял 1.8А (максимально допустимый ток пульсаций составлял 600 мА).

Глядя на кривые спада для каждого индуктора, можно получить следующие рабочие индуктивности:

CTX10-1-52 – 7,5 мкГн

CTX10-1A – 8,0 мкГн

DR74-100 – 9,5 мкГн

CTX10-1-52 уже представляет собой маргинальную конструкцию, поскольку 7,5 мкГн – это минимальная индуктивность, необходимая для достижения максимального тока пульсаций 600 мА. Мы продолжим рассматривать эту часть, чтобы показать производительность устройства с железным порошком.

Во-первых, давайте посмотрим на общие потери и эффективность.Чтобы вычислить потери в сердечнике, вы должны сначала рассчитать приложенные вольт-секунды:

В _л = 1,8 В

dt = V _o / V _IN × 1 / fs = 2,5 мкс

Приложенная вольт-мксекунда = 1,8 В × 2,5 мкс = 4,5 В-мкс

Где

В _l = напряжение индуктора,

В _или = выходное напряжение,

В _IN = входное напряжение,

dt = время включения и

fs = частота переключения.

Если посмотреть на DR73-100, эта деталь имеет номинальное значение 11 вольт-секунд.5 В-мкс при 100 кГц, то есть приложенные вольт-секунды, которые вносят 10% потерь, необходимых для повышения температуры на 40 ° C.

В этом примере компонент используется при среднеквадратичном значении 1,5 А, пике 1,8 А и 4,5 В-мкс. Таким образом, DR73-100 используется при 39% своей вольт-секундной мощности. Глядя на Рис. 4 , вы можете увидеть, что при 200 кГц и 39% приложенных вольт-секунд максимально допустимые потери, возникающие из-за Irms, составляют примерно 96,25% от общих потерь.

Суммарные потери при повышении температуры на 40 ° C равны сопротивлению постоянному току (DCR), умноженному на квадрат номинального значения Irms, то есть для DR73-100;

Потери при повышении температуры на 40 ° C = 0.0634Σ × 2,11 ² = 0,282 Вт

В нашем примере потери из-за Irms должны быть уменьшены до 96,25% от этого повышения на 40 ° C, что дает нам требуемые потери Irms в 0,271 Вт. Исходя из этого, вы можете рассчитать максимально допустимый среднеквадратичный ток, равный 2,03 А. Вы также знаете, что потери в сердечнике составляют примерно 11 мВт (разница между потерями при повышении температуры на 40 ° C и требуемыми потерями Irms в 0,271 Вт).

Повторение этой процедуры для CTX10-1-52 и CTX10-1A может дать вам результаты, показанные в Таблица 2 , на странице 28.

Взвешивание плюсов и минусов

У всех трех катушек индуктивности рассеиваемая мощность меньше, чем требуется для повышения температуры на 40 ° C. Таким образом, тепловые характеристики не должны быть проблемой для большинства приложений. На практике потери в индукторе будут выше расчетных. Это связано с тем, что вы не учли потери в обмотке переменного тока из-за скин-эффекта и эффекта близости. Эти потери становятся более значительными с увеличением тока пульсаций и увеличением частоты, но обычно они меньше, чем потери I ² R.Рассматривая каждую из альтернатив, вы можете взвесить плюсы и минусы каждого индуктора и определить приложения, которые им подходят лучше всего.

CTX10-1-52 : Конструкция тороида из железного порошка означает наилучшие возможные характеристики электромагнитных помех от так называемой конструкции с замкнутым полем. Короче говоря, здесь нет паразитного магнитного поля. Это также означает низкую стоимость, поскольку железный порошок является самым дешевым из доступных материалов сердечника. Однако высокие потери в сердечнике и практический предел рабочей частоты 300 кГц делают железный порошок непригодным для большинства портативных приложений.Более высокие рабочие частоты, превышающие 1 МГц, обычно используются для уменьшения размера требуемого индуктора в этих изделиях. Тороиды из железного порошка представляют собой хорошее экономичное решение в приложениях с высокой мощностью, где требуются высокие значения индуктивности и номинальные токи.

CTX10-1A : Это явный победитель, когда дело касается эффективности. Использование сердечника с высокой проницаемостью означает, что требуется меньше витков, и, как таковая, DCR обмотки является низким. В сочетании с разумными потерями в сердечнике даже на частотах выше 500 кГц аморфное решение обеспечивает общие потери, составляющие менее 5% выходной мощности.Однако это решение связано с двумя проблемами: аморфные материалы дороги и, как правило, обладают плохой температурной стабильностью. Это делает их непригодными для использования при высоких температурах окружающей среды. Для более дешевого решения, которое по-прежнему обеспечивает лучшую производительность, чем порошок железа, вам следует рассмотреть возможность использования MPP или Sendust. Эти материалы предлагают как более низкие потери, так и более высокую частоту работы, чем железный порошок, с умеренными затратами.

DR73-100 : Катушки индуктивности с ферритовым сердечником барабана предлагают самую низкую общую стоимость в очень энергоемкой упаковке, что делает их наиболее популярным выбором для преобразователей малой мощности в портативных, компьютерных и телекоммуникационных приложениях.Использование феррита означает, что возможна работа на высоких частотах, превышающих 1 МГц, что позволяет использовать более низкие значения индуктивности и детали меньшего размера. Единственная проблема с конструкцией сердечника барабана – это электромагнитные помехи, поскольку сердечники барабана имеют значительное поле рассеяния. За исключением наиболее чувствительных приложений, эту проблему можно решить с помощью устройства с магнитным экранированием, такого как DR73.

Конструкции

Тороид и сердечник барабана обеспечивают необходимое решение в большинстве применений импульсных регуляторов. Однако в сильноточных приложениях решения с сердечниками E и U / I позволяют использовать медную фольгу для снижения потерь I ² R.Для нашего примера лучшим решением является экранированный барабан. Эта часть предлагает самое компактное и дешевое решение с приемлемыми характеристиками EMI. Производительность EMI можно было обменять на небольшую рентабельность, но для получения более эффективного решения потребовалось бы непропорциональное увеличение затрат при небольшом улучшении.

Для получения дополнительной информации об этой статье, CIRCLE 337 на сервисной карте считывателя

Калькулятор накопления энергии индуктора

Вам интересно, на что способен этот калькулятор накопления энергии индуктора? Что ж, он оценивает энергию, запасенную в катушке индуктивности, когда через нее проходит электрический ток .Мы также предоставляем уравнение для магнитной энергии в соленоиде и откуда взялось это уравнение для энергии. Далее по тексту вы также найдете полезную информацию о том, как это явление используется на практике.

Магнитная энергия, запасенная в катушке, формула

Предполагая, что у нас есть электрическая цепь, содержащая источник питания и соленоид индуктивности L , мы можем записать уравнение магнитной энергии E , хранящейся в индукторе, как:

E = 1/2 * L * I² ,

, где I – ток, протекающий по проводу.

Другими словами, мы можем сказать, что эта энергия равна работе, совершаемой источником энергии для создания такого магнитного поля.

Как мы видим, энергия, запасенная в катушке индуктивности, зависит от тока второй мощности. Это говорит нам о том, что соленоид предотвращает внезапный скачок тока в цепи, и именно по этой причине мы можем видеть искру при отключении некоторых электронных устройств.

Как пользоваться калькулятором накопления энергии индуктора?

Допустим, у нас есть цепь, содержащая источник питания и катушку индуктивности L = 20 мкГн .Мы ищем энергию, запасенную в катушке индуктивности, когда мы пропускаем через систему постоянный ток I = 300 мА .

Если вы не хотите портить единицы измерения, давайте запишем все значения в экспоненциальном представлении: L = 2 · 10⁻⁵ H , I = 3 · 10⁻¹ A
Используйте формулу для магнитной энергии в соленоиде: E = 1/2 * 2 · 10⁻⁵ H * (3 · 10⁻¹ A) ² = 9 · 10⁻⁷ J
Энергия, запасенная в катушке индуктивности, также может быть записана как E = 0.9 мкДж или 900 нДж
Вы всегда можете использовать этот калькулятор накопления энергии индуктора, чтобы убедиться, что ваш результат верен!

Иногда нам может потребоваться больше энергии для нашего приложения. Единственное, что мы можем сделать, – это увеличить индуктивность, добавив материал с высокой магнитной проницаемостью, например ферромагнитные сердечники.

Применение накопителей магнитной энергии

Одно из основных применений этой накопленной магнитной энергии – в LC-цепях (содержащих как индуктивность, так и емкость).В этих случаях энергия, запасенная в катушке индуктивности, преобразуется в электрическую энергию конденсатора и наоборот. Система может быть настроена на отправку и прием радиосигналов, когда колебания тока достигают резонансной частоты радиоволн.

Катушки индуктивности

также широко используются в трансформаторах, которые изменяют амплитуду напряжения от одной цепи к другой. Магнитная энергия от одной катушки переносится на вторую через мягкую ферромагнитную среду. Благодаря этому у нас есть удобный и безопасный доступ к электричеству в наших городах и домах.

Выбор индукторов для энергоэффективных силовых приложений

Энергоэффективность в источниках питания может быть связана как с индукторами, так и с топологией схемы. Несколько простых расчетов помогут предотвратить неприятные сюрпризы.

CHRIS HARE,
LEONARD CRANE
COILCRAFT, INC.
В высокочастотных преобразователях постоянного и постоянного тока катушки индуктивности отфильтровывают пульсации переменного тока, наложенные на выход постоянного тока. Независимо от того, понижает ли преобразователь напряжение – понижает – или увеличивает – усиливает – или одновременно увеличивает и понижает – SEPIC – индуктор сглаживает пульсации, чтобы обеспечить выходной сигнал псевдо-постоянного тока.

Приложения с батареями могут продлить срок службы батарей за счет повышения эффективности всей цепи питания, а эффективность индуктора часто является основной частью конструкции. Тщательный учет эффективности индуктора может означать разницу между тем, чтобы ваша батарея работала, когда она вам нужна, и тем, что она умирала посреди важной задачи.

Эффективность индуктивности наивысшая, когда комбинация потерь в сердечнике и обмотке минимальна. Следовательно, максимальная эффективность достигается за счет выбора индуктора, который обеспечивает достаточную индуктивность для сглаживания пульсаций тока при одновременном минимизации потерь.Индуктор должен пропускать ток без насыщения сердечника или перегрева обмотки.

Точное прогнозирование потерь в сердечнике и обмотке индуктора может быть довольно сложным. Потери в сердечнике зависят от нескольких факторов, таких как пик-пик пульсаций тока, частота пульсаций тока, материал сердечника, размер сердечника и количество витков. Требуемый ток пульсаций и частота пульсаций зависят от приложения, в то время как материал сердечника, размер сердечника и количество витков зависят от катушки индуктивности.

Наиболее часто используемым уравнением для характеристики потерь в сердечнике является уравнение Стейнмеца:

P _{сердцевина} = K (f) ^x (B) ^y

Где P _{сердечник} = потери мощности в сердечнике, Вт; K, x, y = постоянные материала сердечника; f = частота, Гц; и B = плотность потока, Т.Это уравнение показывает, что потери в сердечнике зависят от частоты f и плотности потока B. Плотность потока зависит от тока пульсаций, поэтому оба параметра зависят от области применения. Уравнение также показывает, что потери в сердечнике зависят от катушки индуктивности, где материал сердечника определяет константы K, x и y. Обратите внимание, что плотность магнитного потока также является функцией площади сердечника (A _e) и количества витков (N), поэтому потери в сердечнике зависят как от приложения, так и от индуктора.

Для сравнения, потери постоянного тока в обмотках вычислить несложно:

P _{постоянного тока} = l _{постоянного тока} ² × R _{постоянного тока}

Где P _dc = рассеиваемая мощность постоянного тока, Вт; l _dc = действующее значение постоянного тока индуктора, А; и R _dc = сопротивление обмотки индуктора постоянному току, Ом.

Потери в обмотке переменного тока более сложны и могут включать эффекты повышенного сопротивления на более высокой частоте, вызванные как скин-эффектом, так и эффектом близости. Кривые ESR (эффективное последовательное сопротивление) или ACR (сопротивление переменному току) могут показывать некоторое увеличение сопротивления на более высокой частоте. Однако эти кривые обычно строятся при низких уровнях тока, поэтому они не отражают зависящие от тока потери (в сердечнике). Они также могут быть неправильно истолкованы.

Быстрый взгляд на кривую зависимости ESR от частоты показывает, что сопротивление выше 1 МГц выглядит большим.Это убедительно свидетельствует о том, что эта часть не может или не должна использоваться на этой частоте из-за высоких потерь от ESR. Однако было замечено, что детали с такими кривыми хорошо себя зарекомендовали в реальных преобразователях – намного лучше, чем можно было бы предположить по этим кривым.

Например, рассмотрите кривую зависимости ESR от частоты на прилагаемом рисунке. Первое наблюдение: сопротивление выше 1 МГц выглядит большим. Такое поведение убедительно свидетельствует о том, что индуктор не должен использоваться на этой частоте из-за высоких потерь от ESR.Однако было замечено, что детали с такими кривыми хорошо себя зарекомендовали в реальных преобразователях – намного лучше, чем можно было бы предположить по кривым.

Рассмотрим следующий пример. Предположим, что преобразователь должен обеспечивать выходное напряжение 5 В при 0,3 А (1,5 Вт). Мы используем катушку индуктивности Coilcraft 10 мкГн с типичным значением ESR в зависимости от частоты, как показано на прилагаемом рисунке. Если преобразователь работает на частоте 250 кГц, график показывает, что ESR, которое включает сопротивление как переменного, так и постоянного тока, составляет примерно 0,8 Ом.
Для понижающего преобразователя средний ток индуктивности равен току нагрузки, 0.3 А.

Можем посчитать потери в катушке индуктивности:

л ² R = (0,3) ² × (0,8) = 0,072
0,072 ÷ 1,5 = 0,048 ~ 5%

Таким образом, примерно 5% выходной мощности теряется в катушке индуктивности. Однако, если бы мы использовали тот же преобразователь на частоте 5 МГц, мы могли бы видеть из кривой ESR, что R составляет от 10 до 20 Ом. Если принять R = 10 Ом, потери мощности в катушке индуктивности должны составить:

л ² R = (0,3) ² × (10) = 0,9
0,9 ÷ 1.5 = 0,60

Таким образом, 60% выходной мощности теряется в катушке индуктивности! На этом простом примере может показаться очевидным, что дизайнер не должен выбирать такой компонент.

Было замечено, что преобразователи, на самом деле, часто имеют лучшую производительность, чем предсказывают кривые ESR. Следующее объяснение показывает, почему.

Упрощенная версия возможной формы сигнала понижающего преобразователя с непрерывной проводимостью показывает пульсации тока, которые относительно малы по сравнению со средним током.

На следующем рисунке показана упрощенная версия возможной формы сигнала понижающего преобразователя с непрерывной проводимостью. Ток пульсаций относительно невелик по сравнению со средним током.

Предположим, что пик-пик пульсации тока составляет около 10% от среднего значения тока. Из предыдущего примера это означает, что I _dc = 0,3 A и I _p-p = 0,03 A. Чтобы правильно спрогнозировать потери в катушке индуктивности, ток должен быть разделен на две составляющие. Для низкочастотных потерь или потерь постоянного тока мы используем низкочастотное сопротивление (фактически R _dc), которое, как видно на графике, равно 0.7 Ом. Ток – это действующее значение тока нагрузки плюс ток пульсации. В этом случае ток пульсаций невелик, поэтому значение приблизительно равно току нагрузки постоянного тока
.
‘
Чтобы получить общие потери, мы должны добавить низкочастотные потери к высокочастотным потерям, которые составляют I ² R. В этом случае R – это ESR, а I – среднеквадратичное значение пульсирующего тока. Только.

Приблизительный среднеквадратичный ток пульсаций = l ^p-p ÷ 2√3 = 0,03 ÷ 3,464 = 0,0087 A. При 250 кГц потери переменного тока будут: I ² R = (0.0087 A) ² × (0,8 Ом) = 0,00006 Вт.
I ² R = (0,0087 A) ² × (10 Ом) = 0,00076 Вт.

Таким образом, на частоте 250 кГц мы прогнозируем, что общие потери в катушке индуктивности составят 0,063 Вт + 0,00006 Вт = 0,06306 Вт. Мы видим, что работа на частоте 250 кГц прогнозирует лишь немного большие потери (менее 1%), чем просто предсказывает R _dc.

Теперь давайте посмотрим на тот же пример на частоте 5 МГц. Потери на низких частотах остались прежними 0,063 Вт. При расчете потерь переменного тока необходимо использовать ESR, которое ранее было оценено как 10 Ом:

Низкочастотные потери = l _dc ² R = (0.3) 2 × (0,7) = 0,063 Вт

Таким образом, общие потери в катушке индуктивности на частоте 5 МГц составляют 0,063 Вт + 0,00076 Вт = 0,06376 Вт. ESR по всему току нагрузки. Кроме того, этот пример не совсем справедлив, потому что мы не будем использовать то же значение индуктивности на 5 МГц, как на 250 кГц. Мы бы использовали гораздо меньшую L и, следовательно, получили бы гораздо меньший R _dc.

Таким образом, потери в катушке индуктивности должны быть рассчитаны с помощью комбинации R _dc и ESR. Потери будут разумными для преобразователя в режиме непрерывного тока, в котором ток пульсаций мал по сравнению с током нагрузки.

В типичных приложениях пульсирующий ток поддерживается примерно на уровне 40% от тока нагрузки или меньше. Независимо от содержания пульсаций, кривые ESR не фиксируют зависящие от тока потери в сердечнике при более высоком токе. А общие потери в катушке индуктивности определяют общую эффективность катушки индуктивности.

Таким образом, производители индукторов оптимизируют эффективность индукторов, выбирая материалы с низкими потерями и проектируя индукторы с минимальными общими потерями. Использование прямоугольного «плоского» провода может обеспечить наименьшее Rdc данного размера для минимизации потерь постоянного тока. Улучшение материалов сердечника привело к созданию катушек индуктивности с низкими потерями в сердечнике на переменном токе на высоких частотах, что привело к повышению эффективности катушек индуктивности.

Например, Coilcraft только что выпустила серию формованных силовых индукторов XEL, оптимизированных для высокочастотных приложений с высоким пиковым током.Эти катушки индуктивности предназначены для мягкого насыщения, обеспечивая при этом самые низкие потери на переменном токе на частотах 2 МГц и выше.

Кривые зависимости индуктивности от тока для значения 2,2 мкГн в сериях индукторов XEL, XAL и XFL от Coilcraft. Потери переменного тока и общие потери для серий индукторов XEL, XAL и XFL от Coilcraft на частоте 3 МГц. Хотя индуктор XFL имеет самые низкие общие потери мощности, индуктор XEL имеет более низкие общие потери, чем XAL, и поэтому является лучшим выбором для приложений с высокочастотными преобразователями мощности, которые должны выдерживать высокий пиковый ток.

Соседний график зависимости индуктивности от токовых характеристик соответствует значению 2,2 мкГн в сериях XEL, XAL и XFL. Серии XEL и XAL, безусловно, являются лучшим выбором для удержания индуктивности при токах около 3 А или выше. На другом соседнем графике сравниваются потери переменного тока и общие потери тех же катушек индуктивности на частоте 3 МГц.Хотя у катушки индуктивности XFL самые низкие общие потери мощности, новая катушка индуктивности XEL имеет более низкие общие потери, чем XAL, и поэтому является лучшим выбором для высокочастотных преобразователей мощности, которые должны выдерживать высокий пиковый ток.

Чтобы ускорить процесс проектирования для инженеров, выбирающих катушки индуктивности, компания Coilcraft разработала инструменты, которые вычисляют потери в сердечнике и обмотке на основе измерений для каждого возможного условия применения. Результаты этих инструментов включают в себя зависящие от тока и частоты потери в сердечнике и обмотке, что устраняет необходимость запрашивать фирменную информацию о конструкции индуктора, такую как материал сердечника, A _e и количество витков, а также необходимость выполнять ручные вычисления. .

Для преобразователей постоянного / постоянного тока селектор индуктивности преобразователя постоянного тока в постоянный ток компании Coilcraft рассчитывает значение индуктивности, пиковый ток и требования к пик-пиковому току на основе рабочих условий и величины выбранного переменного тока пульсаций. Затем он передает эту информацию в инструмент Power Inductor Finder для отображения списка катушек индуктивности, которые могут соответствовать этим требованиям. Список включает индуктивность при пиковом токе, номинальный ток, общие потери и результирующую температуру детали для каждого указанного индуктора.
Если вы уже знаете значение индуктивности и номинальный ток, необходимые для вашего приложения, вы можете ввести эту информацию непосредственно в средство поиска силовых индукторов.Результаты включают в себя (общие) потери в сердечнике и обмотке и номинальные значения тока насыщения для каждого индуктора, чтобы убедиться, что индуктивность останется близкой к проектным требованиям в условиях пикового тока для вашего приложения.
Инструмент также можно использовать для построения графика зависимости индуктивности от тока для сравнения традиционных индукторов с жестким насыщением и типов с мягким насыщением.

Конструкция с максимальной эффективностью требует выбора катушек индуктивности с наименьшими общими потерями в рабочих условиях.Расчет общих потерь может быть сложным, но эти расчеты встроены в инструменты Power Magnetics компании Coilcraft, что делает выбор, сравнение и анализ настолько простым, насколько это возможно.

ССЫЛКИ
Характеристики индуктора в высокочастотных преобразователях постоянного / постоянного тока, Лен Крейн, Документ 470-2, 2015 г.

XEL, XAL или XFL? – Сделать лучший выбор

Селектор индуктивности DC-DC Coilcraft, инструменты Power Magnetics

Искатель силового индуктора Coilcraft, инструменты Power Magnetics

Конструкция выходного дросселя

и расчет для ИИП

Из этой статьи вы узнаете, как спроектировать индуктивность с ферритовым сердечником для импульсных источников питания. Как спроектировать индуктор для преобразователя постоянного тока в постоянный, такого как понижающий преобразователь , повышающий преобразователь , повышающий преобразователь , преобразователь cuk и мост H ? Прочитав эту статью, вы сможете спроектировать выходной индуктор для любой топологии SMPS.Выходные индукторы также используются в инверторе с чистой синусоидой в LC-фильтре для удаления гармоник из синусоидальной волны. Конструкция выходного дросселя и конструкция ферритового трансформатора являются двумя наиболее важными компонентами в проектах силовой электроники . потому что их непросто создать. Для этого требуются профессиональные намоточные станки. Но все же вы можете спроектировать их, приложив немного усилий.

Метод расчета выходной индуктивности остается одинаковым для всех топологий силовой электроники.Выходной индуктор используется для хранения энергии нагрузки, когда входное питание отключено. В электрических терминах выходной дроссель преобразует прямоугольные коммутационные импульсы в постоянный ток. После катушки индуктивности конденсатор производит чистое выходное напряжение постоянного тока. Спроектировать выходной дроссель очень просто. В выходной катушке индуктивности используется тороидный сердечник Usullay с воздушным зазором. Формула расчета выходной индуктивности приведена ниже:

L (мин) = [Vin (макс) – Vout] * Toff (расчет) / 1,4 * Iout (мин)

Где Vin (max) – максимальное пиковое напряжение выходного выпрямителя.Vout – выходное напряжение. Toff (est) – время включения преобразователя при максимальном входном напряжении. Iout (min) – минимальный ток нагрузки. Все вышеуказанные параметры должны быть известны. Таким образом, вы можете легко рассчитать индуктивность, используя приведенную выше формулу. L (мин) – это минимально необходимая индуктивность. Теперь мы знаем минимальную индуктивность, теперь нам нужно рассчитать количество витков для тороидального сердечника. Таким образом, мы можем спроектировать выходной дроссель с необходимым количеством витков. Формула для расчета необходимого количества оборотов приведена ниже:

AL = L / N²

AL можно найти в паспорте сердечника.Где L – минимальная индуктивность, а N – необходимое количество витков. При изменении приведенной выше формулы количество витков становится:

Расчет катушки индуктивности онлайн калькулятор

Расчёт катушки индуктивности под динамик

Расчет катушек индуктивности в 3D с помощью COMSOL Multiphysics

Базовые принципы работы катушки индуктивности

Оптимизация катушки индуктивности

3D-моделирование катушки индуктивности в COMSOL Multiphysics

Постобработка и анализ результатов расчёта модели индуктора

Учёт термических эффекто в модели катушки индуктивности

Узнайте больше о моделировании индукционных устройств в COMSOL Multiphysics

Конструкторский расчет катушки индуктивности (стр. 1 из 4)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Катушки индуктивности | Онлайн журнал электрика

Расчет катушки индуктивности колебательного контура и обоснование выбора материалов.

Содержание

Индуктивность | Физика II

Как избежать насыщения индуктора в конструкции источника питания | Статья

Причины насыщения индуктора

Советы по оценке насыщения индуктора:

Метод 1. Расчет плотности магнитного потока

Метод 2: Расчет максимального тока индуктора

Метод 3. Определить, насыщен ли индуктор кривой тока индуктора

Метод 4: Измерьте аномальное повышение температуры индуктора и прислушайтесь к звукам

• Калькуляторы электрического, радиочастотного и электронного оборудования • Онлайн-преобразователи единиц измерения

Руководство по выбору индукторов для импульсных регуляторов

Рекомендации по понижающему преобразователю

Выбор индуктора

Номинальный ток индуктора

Потери в сердечнике и температура

Окончательный отбор

Взвешивание плюсов и минусов

Магнитная энергия, запасенная в катушке, формула

Как пользоваться калькулятором накопления энергии индуктора?

Применение накопителей магнитной энергии

Выбор индукторов для энергоэффективных силовых приложений

и расчет для ИИП

Добавить комментарий Отменить ответ

Расчет катушки индуктивности: Расчет катушки индуктивности | Онлайн калькулятор

Расчет катушки индуктивности онлайн калькулятор

Расчёт катушки индуктивности под динамик

Расчет катушек индуктивности в 3D с помощью COMSOL Multiphysics

Базовые принципы работы катушки индуктивности

Оптимизация катушки индуктивности

3D-моделирование катушки индуктивности в COMSOL Multiphysics

Постобработка и анализ результатов расчёта модели индуктора

Учёт термических эффекто в модели катушки индуктивности

Узнайте больше о моделировании индукционных устройств в COMSOL Multiphysics

Конструкторский расчет катушки индуктивности (стр. 1 из 4)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Катушки индуктивности | Онлайн журнал электрика

Расчет катушки индуктивности колебательного контура и обоснование выбора материалов.

Содержание

Индуктивность | Физика II

Как избежать насыщения индуктора в конструкции источника питания | Статья

Причины насыщения индуктора

Советы по оценке насыщения индуктора:

Метод 1. Расчет плотности магнитного потока

Метод 2: Расчет максимального тока индуктора

Метод 3. Определить, насыщен ли индуктор кривой тока индуктора

Метод 4: Измерьте аномальное повышение температуры индуктора и прислушайтесь к звукам

• Калькуляторы электрического, радиочастотного и электронного оборудования • Онлайн-преобразователи единиц измерения

Руководство по выбору индукторов для импульсных регуляторов

Рекомендации по понижающему преобразователю

Выбор индуктора

Номинальный ток индуктора

Потери в сердечнике и температура

Окончательный отбор

Взвешивание плюсов и минусов

Магнитная энергия, запасенная в катушке, формула

Как пользоваться калькулятором накопления энергии индуктора?

Применение накопителей магнитной энергии

Выбор индукторов для энергоэффективных силовых приложений

и расчет для ИИП

Больше новостей

Добавить комментарий Отменить ответ