Калькулятор расчета индуктивности катушки без сердечника — MOREREMONTA
Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла.
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.
Сайт для радиолюбителей
Как известно индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки. Чем больше диаметр, длина намотки и число витков тем больше индуктивность.
Для определения индуктивности уже готовой катушки заполните предложенную форму для расчета, в ней необходимо указать диаметр катушки, длину намотки и число витков.
Если необходимо намотать катушку определенной индуктивности, то можно рассчитать кол-во витков катушки исходя из диаметра катушки и длины намотки.
Если по результатам расчета окажется, что у Вас нет провода нужного диаметра, то можно взять ближайший по диаметру в большую или меньшую сторону (не более чем на 25%) и сделать перерасчет.
Катушка индуктивности представляет собой электрическую сборную конструкцию, которая может изготавливаться в следующих исполнениях:
- В виде намотанной на каркас обмотки из провода определенного диаметра.
- Как витая бескаркасная спираль, предварительно сформированная на твердой основе, а затем снятая с нее.
- Катушка, намотанная многослойным проводом в специальной матерчатой изоляции.
Особенностью этого электротехнического компонента является наличие у него значительной по величине индуктивности при относительно малой емкостной составляющей и низком активном сопротивлении. Это приводит к тому, что при протекании переменного тока она проявляет себя как элемент, обладающий большой инерционностью.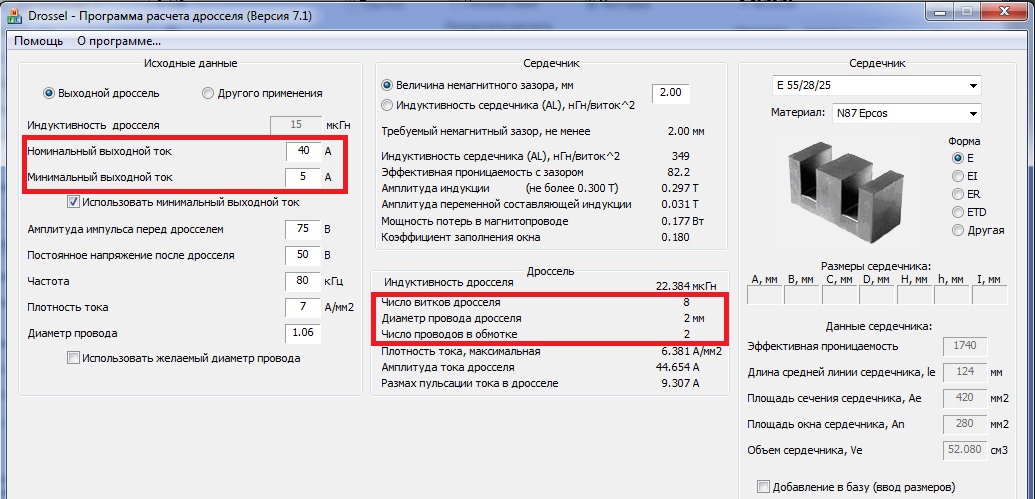
Обратите внимание: Благодаря этой особенности катушки текущий по ней ток отстает от приложенного напряжения на определенный угол (90 градусов). У профессионалов это явление получило название «отставание по фазе».
Для того, чтобы получить точные значения индуктивности катушки заданной формы, следует ввести ее основные параметры в онлайн-калькулятор. В нем автоматически рассчитывается такой важный показатель, как число витков в данном изделии. После ввода данных в специальную форму вы мгновенно получите искомое значение.
Наш онлайн-калькулятор производит автоматизированный расчет значений катушки индуктивности без сердечника с использованием метода эллиптических интегралов Максвелла. Калькулятор предусматривает расчет значений как однослойных обмоток, так и многослойных.
А вот формула индуктивности:
- L – индуктивность;
- D – диаметр витка;
- N – число витков;
- h – длина намотки;
- g – количество слоев
Преимущества расчета значений параметров катушки с помощью онлайн-калькулятора очевиден.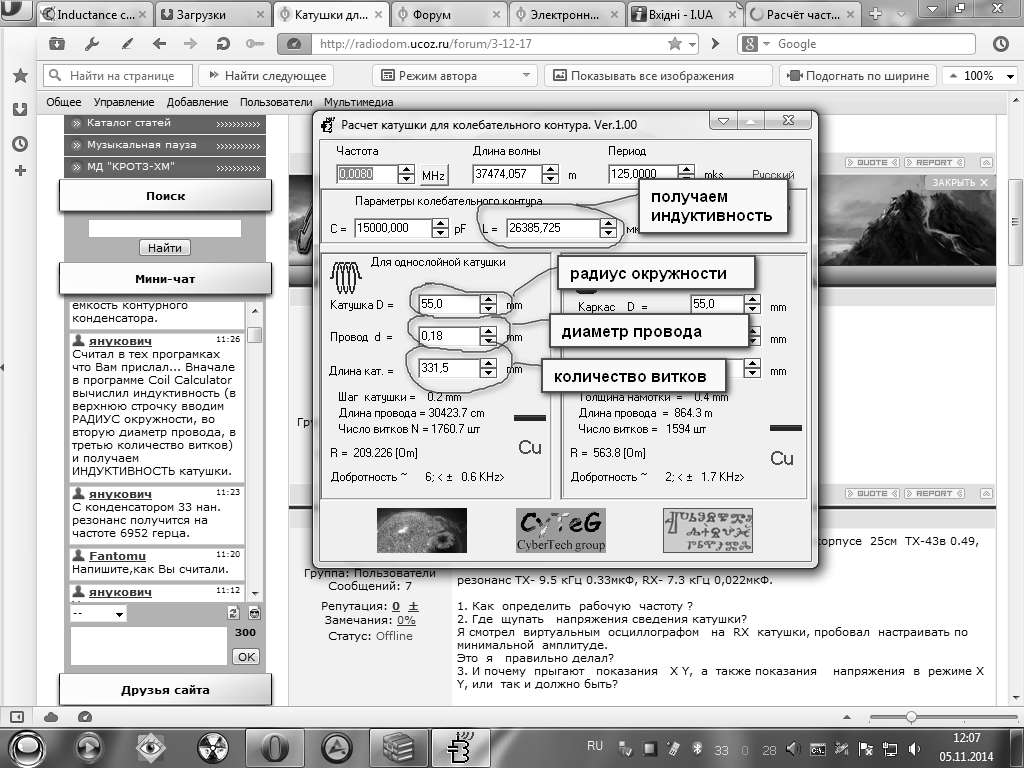
расчет катушки на ферритовом стержне
Программа позволяет производить расчет следующих типов катушек индуктивности:
- Одиночный круглый виток
- Однослойная виток к виткуВ качестве начальных параметров при расчете катушки можно выбрать два варианта:
- Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
- Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
- Однослойная катушка с шагом
- Катушка с не круглой формой витков
- Многослойная катушка В качестве начальных параметров при расчете катушки можно выбрать два варианта:
- Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки («сколько надо отрезать»).
- Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода и приблизительная длина провода для намотки.

- Тороидальная однослойная катушка
- Катушка на ферритовом кольце
- Катушка в броневом сердечнике(Ферритовом и карбонильном)
- Тонкопленочная катушка(Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)
Подробнее о Coil32 …
Довольно часто перед радиолюбителем встает вопрос: » Как рассчитать индуктивность катушки?». Катушки используются и в высокочастотной связной аппаратуре, и при конструировании акустических систем, и даже взглянув на материнскую плату компьютера, Вы и там обнаружите индуктивные элементы. С помощью программы Coil32 можно быстро рассчитать индуктивность катушки. В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки можно «не отходя от кассы» рассчитать емкость конденсатора в колебательном контуре.
В чем преимущества программы перед аналогами?
- Программа рассчитывает индуктивность многих типов катушек. Можно подобрать оптимальный вариант, либо пересчитать катушку под имеющийся каркас.
- Результаты всех расчетов выводятся в текстовое поле, откуда их можно сохранить в файл. В дальнейшем Вы можете их просмотреть, чтобы не пересчитывать заново. Можно открыть этот файл в «MS Word» и распечатать.
- Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
- Рассчитываются основные параметры колебательного контура для однослойной катушки
- Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце
- Для катушек в броневых сердечниках есть возможность выбрать один из нескольких стандартных, что позволяет рассчитать катушку несколькими щелчками мыши.
- Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.

- В Сети часто встречаются программы для расчета индуктивности, работающие под DOS, о преимуществах Windows-интерфейса, думаю, говорить не приходится.
- Программа имеет возможность расширения функционала с помощью дополнительных плагинов для расчета индуктивностей
- Программа имеет мультиязычный интерфейс и скины, дополнительные наборы скинов можно найти на .
Программа распространяется в стиле «Portable» и не имеет установщика. Для установки программы распакуйте архив программы в любой каталог и запустите на выполнение файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.
Калькулятор взаимной индукции
Этот калькулятор определяет взаимоиндукцию двух связанных катушек индуктивности.
Пример. Рассчитать взаимную индуктивность двух расположенных рядом катушек индуктивности 10 мкГн и 5 мкГн с коэффициентом связи 0,5.
Входные данные
Индуктивность первой катушки, L1
генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)
Индуктивность второй катушки, L2
миллигенри (мГн)
Коэффициент связи, k
0 ≤ k ≤ 1
Выходные данные
Взаимоиндукция
M миллигенри (мГн)
Введите величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать.
В токоизмерительных клещах с разъемным магнитопроводом для безопасного измерения тока без необходимости подключать прибор к схеме используется измерительный трансформатор. В приборе используется явление взаимной индукции. На разъемном магнитопроводе надета катушка, являющаяся вторичной обмоткой измерительного трансформатора. Первичной «обмоткой» является охватываемый магнитопроводом провод с током. Электродвижущая сила, возникающая в катушке на магнитопроводе, пропорциональна току, текущему в проводнике, охваченном клещами. Прибор измеряет напряжение на зажимах катушки и указывает на дисплее значение измеряемого тока.
Калькулятор определит взаимоиндукцию M двух связанных катушек индуктивности по формуле:
где k — коэффициент связи, L₁ — индуктивность первой катушки и L₂ — индуктивность второй катушки. Коэффициент связи определяется как отношение взаимоиндукции двух катушек к максимально возможному значению их взаимоиндукции. Коэффициент связи изменяется в пределах от 0 до 1 и зависит от близости катушек или обмоток, материала их сердечника, их взаимной ориентации, формы и количества витков. У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.
У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.
Тороидальные трансформатор и дроссель в импульсном блоке питания
Пример расчетов. Коэффициент связи двух катушек с индуктивностью 2 мкГн и 3 мкГн равен 0,5. Взаимоиндукция в микрогенри определяется как
Две катушки с взаимной индукцией на принципиальной схеме
При увеличении электрического тока, протекающего через катушку индуктивности L₁ от внешней цепи, вокруг катушки создается увеличивающееся магнитное поле, в котором сохраняется энергия. При уменьшении тока магнитное поле также уменьшается. При этом на выводах катушки возникает напряжение (ЭДС самоиндукции) в направлении, противоположном направлению тока, и сохраняемая в магнитном поле энергия отдается обратно во внешнюю цепь. Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).
Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).
Взаимоиндукция в вашем автомобиле: для создания искры в свечах зажигания используется катушка зажигания, представляющая собой трансформатор с высоким коэффициентом трансформации. Когда ток через первичную обмотку с малым числом витков прерывается, очень большая ЭДС возникает во вторичной обмотке с большим числом витков, которая достаточна для создания искры в зазоре автомобильной свечи зажигания
В обратной ситуации, если ток течет в катушке L₂, а наводится ток в катушке L₁, взаимоиндукция будет той же. Отметим, что электродвижущая сила (ЭДС) возникает только при изменении тока, причем чем быстрее изменяется ток, тем больше будет ЭДС. То есть, ЭДС взаимной индукции прямо пропорциональна скорости изменения тока
Явление взаимной индукции используется в трансформаторах, электродвигателях, генераторах и других устройствах, в которых для функционирования необходимо взаимодействие с магнитным полем. В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.
В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.
Расчет катушек на кольцах Amidon из порошкового железа:
Ферритовые кольца фирмы Amidon не имеют цветовой маркировки (блестящие черные либо тускло-серые), Здесь калькулятор для их расчета. Изделия из порошкового железа (карбонильного) маркируются цветом в зависимости от материала кольца. – здесь полный набор характеристик. Расчет ведется по формуле:
ВЫБЕРИТЕ КОЛЬЦО:
| Тип материала кольца – | 123678101215171826304052 |
| Типоразмер кольца – | T-5T-10T-12T-16T-20T-25T-30T-37T-44T-50T-68T-80T-94T-106T-130 |
Доступная информация о кольце:
Цветовой код: Материал: Рабочие частоты LC цепей Начальная магнитная проницаемость (μ): Размеры (OD x ID x H): дюймммAL фактор: мкГн/(N/100)2ВВЕДИТЕ ИСХОДНЫЕ ДАННЫЕ:
| L | = мГнмкГннГн | – Требуемая индуктивность |
Рассчитать
Результат:
| N | = | – Число витков |
МАТЕРИАЛ №0: В основном используется на частотах выше 100 МГц. Индуктивность (или число витков), полученная из расчетов, исходя из заданного параметра AL, не может быть достаточно точной и сильно зависит от техники намотки.МАТЕРИАЛ №1: Очень похож на материал №3 за исключением более высокого объемного сопротивления и повышенной стабильности.МАТЕРИАЛ №2: Carbonyl ‘E’ порошковый материал с высоким объемным сопротивлением. Для изготовления высокодобротных катушек на частотах от 2 МГц до 20 МГц.МАТЕРИАЛ №3: Carbonyl ‘HP’ материал с прекрасной стабильностью и добротностью для низких частот от 50 КГц до 500 КГц.МАТЕРИАЛ №6: Carbonyl ‘SF’ материал. Предназначен для катушек с высокой добротностью и температурной стабильностью для частот 20 МГц — 50 МГц.МАТЕРИАЛ №7: Carbonyl ‘TH’ материал. Очень похож на №2 и №6, но имеет более высокую температурную стабильность.МАТЕРИАЛ №8: Этот материал имеет низкие потери в сердечнике и хорошую линейность в условиях высокого смещения по кривой намагничивания.
Индуктивность (или число витков), полученная из расчетов, исходя из заданного параметра AL, не может быть достаточно точной и сильно зависит от техники намотки.МАТЕРИАЛ №1: Очень похож на материал №3 за исключением более высокого объемного сопротивления и повышенной стабильности.МАТЕРИАЛ №2: Carbonyl ‘E’ порошковый материал с высоким объемным сопротивлением. Для изготовления высокодобротных катушек на частотах от 2 МГц до 20 МГц.МАТЕРИАЛ №3: Carbonyl ‘HP’ материал с прекрасной стабильностью и добротностью для низких частот от 50 КГц до 500 КГц.МАТЕРИАЛ №6: Carbonyl ‘SF’ материал. Предназначен для катушек с высокой добротностью и температурной стабильностью для частот 20 МГц — 50 МГц.МАТЕРИАЛ №7: Carbonyl ‘TH’ материал. Очень похож на №2 и №6, но имеет более высокую температурную стабильность.МАТЕРИАЛ №8: Этот материал имеет низкие потери в сердечнике и хорошую линейность в условиях высокого смещения по кривой намагничивания. Хороший высокочастотный материал. Самый дорогой материал.МАТЕРИАЛ №10: Порошковый материал «W». Обеспечивает хорошую добротность и высокую стабильность для частот от 40 МГц до 100 МГц.МАТЕРИАЛ №12: Синтетический оксидный материал, который обеспечивает хорошую добротность и умеренную стабильность для частот от 50 МГц до 200 МГц. Если высокое значение Q имеет первостепенное значение, этот материал является хорошим выбором. Если первостепенное значение имеет стабильность, предпочтительным будет материал № 17.МАТЕРИАЛ №15: Карбонильный материал «GS6». Обладает отличной стабильностью и хорошей добротностью. Хороший выбор для коммерческих частот вещания, где важны «Q» и стабильность.МАТЕРИАЛ №17: Это новый карбонильный материал, который очень похож на материал № 12, но он обладает лучшей температурной стабильностью. Однако по сравнению с материалом № 12 наблюдается небольшая потеря добротности, составляющая около 10% в диапазоне от 50 МГц до 100 МГц.
Хороший высокочастотный материал. Самый дорогой материал.МАТЕРИАЛ №10: Порошковый материал «W». Обеспечивает хорошую добротность и высокую стабильность для частот от 40 МГц до 100 МГц.МАТЕРИАЛ №12: Синтетический оксидный материал, который обеспечивает хорошую добротность и умеренную стабильность для частот от 50 МГц до 200 МГц. Если высокое значение Q имеет первостепенное значение, этот материал является хорошим выбором. Если первостепенное значение имеет стабильность, предпочтительным будет материал № 17.МАТЕРИАЛ №15: Карбонильный материал «GS6». Обладает отличной стабильностью и хорошей добротностью. Хороший выбор для коммерческих частот вещания, где важны «Q» и стабильность.МАТЕРИАЛ №17: Это новый карбонильный материал, который очень похож на материал № 12, но он обладает лучшей температурной стабильностью. Однако по сравнению с материалом № 12 наблюдается небольшая потеря добротности, составляющая около 10% в диапазоне от 50 МГц до 100 МГц. На частотах выше 100 МГц добротность хуже примерно на 20%.МАТЕРИАЛ №18: Этот материал имеет низкие потери в сердечнике, аналогично материалу № 8, но с более высокой проницаемостью и более низкой стоимостью. Хорошие характеристики насыщения при постоянном токе.МАТЕРИАЛ №26: Материал с пониженным содержанием водорода. Обладает наивысшей проницаемостью из всех порошковых материалов. Используется для фильтров электромагнитных помех и дросселей постоянного тока.МАТЕРИАЛ №30: Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №40: Недорогой материал. Имеет характеристики, похожие на очень популярный материал № 26. Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №52: Этот материал имеет более низкие потери в сердечнике при высокой частоте и такую же проницаемость, что и материал № 26.
На частотах выше 100 МГц добротность хуже примерно на 20%.МАТЕРИАЛ №18: Этот материал имеет низкие потери в сердечнике, аналогично материалу № 8, но с более высокой проницаемостью и более низкой стоимостью. Хорошие характеристики насыщения при постоянном токе.МАТЕРИАЛ №26: Материал с пониженным содержанием водорода. Обладает наивысшей проницаемостью из всех порошковых материалов. Используется для фильтров электромагнитных помех и дросселей постоянного тока.МАТЕРИАЛ №30: Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №40: Недорогой материал. Имеет характеристики, похожие на очень популярный материал № 26. Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №52: Этот материал имеет более низкие потери в сердечнике при высокой частоте и такую же проницаемость, что и материал № 26. Популярен для новых конструкций высокочастотных дросселей.
Популярен для новых конструкций высокочастотных дросселей.
Ссылки по теме:
Виды катушек индуктивности
Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:
D1 – внутренний диаметр, D2 – внешний диаметр, Dср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:
если l > Dср – длинная катушка,
если l ср – короткая катушка,
если l ср – очень короткая катушка,
если l = 0 – плоская катушка,
если t ≈ Dср – толстая катушка,
если t ср – тонкая катушка,
если t = 0 – соленоид.
Индуктивность кругового кольца круглого сечения
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид
При этом его индуктивность можно вычислить по следующему выражению
для постоянного тока
где R – радиус витка, м, R = D/2;
r – радиус провода, м, r = d/2;
μ – магнитная постоянная, μ = 4π•10-7 Гн/м.
Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.
Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).
Для постоянного тока индуктивность составит
На частоте 50 кГц
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.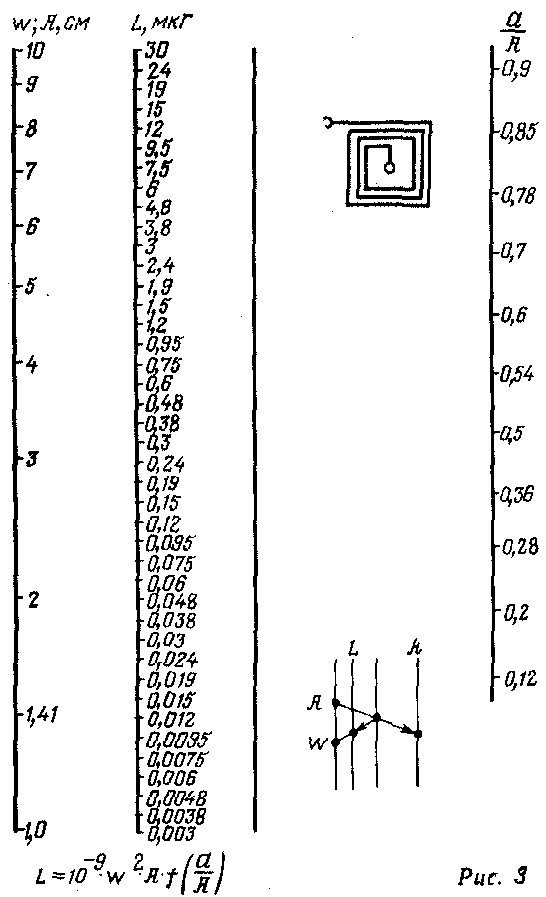
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).
Эквивалентная схема реальной катушки индуктивности
В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.
Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.
Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.
Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками
Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.
Катушки индуктивности и обмотки в различных устройствах
Рассчитать катушку индуктивности с помощью онлайн калькулятора
Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем. Основным её свойством является наличие большой индуктивности при малой емкости и низком активном сопротивлении. В этом обзоре описано, как выполнить самостоятельный расчет катушки индуктивности, какими внешними параметрами она должна обладать, что бы были достигнуты требуемые рабочие параметры.
Калькулятор расчета катушки индуктивности
Индуктивность можно рассчитать самостоятельно или выполнить онлайн расчет с помощью специального калькулятора. Для автоматического расчета наиболее часто используется программа Coil32. Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором. Пользоваться этой программой достаточно просто.
При работе с ней сначала нужно выбрать тип изделия (однослойная или многослойная, с ферритовым сердечником или без него, возможны другие варианты). Задав в калькуляторе расчет геометрических параметров, диаметр провода, число витков, свойства сердечника можно с помощью программы получить ожидаемую индуктивность изделия. Для получения необходимой величины можно в расчетах изменять число витков и диаметр провода.
Собранное изделие по рассчитанным параметрам можно проверить с помощью тестера на соответствие необходимым параметрам. Такой прибор называется LC тестер. Он измеряет индуктивность катушек и ёмкость конденсаторов. При отклонении полученных параметров от заданной величины можно увеличить либо уменьшить количество витков проволоки на изделии.
При желании можно выполнить самостоятельно расчет индуктивности катушки без сердечника или с ним. Единой формулы нет, они строго индивидуальны для каждого случая. В общем случае они прямо пропорциональны количеству витков и диаметру витков. Например, расчет однослойной цилиндрической обмотки выполняют по формуле:
L = (D/10)2*n2/(4.5*D+10*l)
Где L – индуктивность в микро Генри, D – её диаметр в мм, L – длина в мм, n – число витков. Эта эмпирическая формула очень проста, она не учитывает диаметр проволоки, рабочую частоту на которой планируется применять изделие.
Расчет индуктивности катушки с сердечником более сложен. С его добавлением значение индуктивность сильно возрастает. В расчетах в формулу добавляются параметры магнитных свойств сердечника. Ещё более сложными являются формулы расчёта многослойных катушек или катушек тороидальной формы. При редком или первичном использовании лучше всего воспользоваться специальными калькуляторами. Полученные расчеты можно проверить по формулам вручную. В любом случае после изготовления можно проверить параметры собранного изделия и при необходимости их изменить.
Маркировка катушки индуктивности калькулятор – Домострой
Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла.
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.
Сайт для радиолюбителей
Как правило кодовая маркировка дросселей содержит номинальное значение индуктивности и допуск. Номинальное значение индуктивности кодируется цифрами, а допуск буквами.
Первые две цифры указывают значение в мкГн, а последняя — количество нулей. Далее следует буква указывающая допуск.
Допуск обозначается следующими буквами:
D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%
Если последняя буква не указывается — допуск 20%
Для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R
Для индуктивностей меньше 1 мкГн — буква N
Например, код 101J обозначает 100 мкГн ±5%.
| 2N2D — 2,2 нГн ±0,3 нГн | 1R2K — 1,2 мкГн ±10% | 470K — 47 мкГн ±10% |
| 22N — 22 нГн | 2R2K — 2,2 мкГн ±10% | 680K — 68 мкГн ±10% |
| R10M — 0,10 мкГн ±20% | 3R3K — 3,3 мкГн ±10% | 101K — 100 мкГн ±10% |
| R15M — 0,15 мкГн ±20% | 4R7K — 4,7 мкГн ±10% | 151K — 150 мкГн ±10% |
| R22M — 0,22 мкГн ±20% | 6R8K — 6,8 мкГн ±10% | 221K — 220 мкГн ±10% |
| R33M — 0,33 мкГн ±20% | 100K — 10 мкГн ±10% | 331K — 330 мкГн ±10% |
| R47M — 0,47 мкГн ±20% | 150K — 15 мкГн ±10% | 471J — 470 мкГн ±10% |
| R68M — 0,68 мкГн ±20% | 220K — 22 мкГн ±10% | 681J — 680 мкГн ±10% |
| 1R2K — 1,2 мкГн ±20% | 330K — 33 мкГн ±10% | 102 — 1000 мкГн ±10% |
Онлайн калькулятор кодового обозначения дросселей
Цветовая маркировка дросселей
Наиболее часто применяется кодировка 4 или 3 цветными кольцами или точками. Первые две метки указывают на значение номинальной индуктивности в микрогенри, третья метка — множитель, четвертая — допуск. В случае кодирования 3 метками подразумевается допуск 20%. Цветное кольцо, обозначающее первую цифру номинала, может быть шире, чем все остальные.
Обычно для индуктивностей кодируется номинальное значение индуктивности и допуск, т.е. допускаемое отклонение от указанного номинала. Номинальное значение кодируется цифрами, а допуск — буквами.
Применяется два вида кодирования.
А . Первые две цифры указывают значение в микрогенри (мкГн, uН), последняя — количество нулей. Следующая за цифрами буква указывает на допуск. Например, код 101J обозначает 100 мкГн ±5%. Если последняя буква не указывается — допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.
Допуск: D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%
В . Индуктивности маркируются непосредственно в микрогенри (мкГн, uН). В таких случаях маркировка 680К будет означать не 68 мкГн ± 10 %, как в случае А, а 680 мкГн ± 10%.
Электромагнитный расчет и оптимизация планарных катушек на печатных платах
Планарные катушки используются в самых различных устройствах — от датчиков артериального давления до платежных карт. Они располагаются на печатных платах и хорошо подходят для создания взаимных индуктивных связей, особенно при ограниченном пространстве. При проектировании таких катушек важно точно рассчитать как индуктивность, так и активное сопротивление, так как эти факторы играют ключевую роль в производительности устройства. Для эффективного описания катушек на плоскости инженеры могут использовать технологию задания многослойных оболочек (layered shell), доступную в пакете COMSOL®.
Планарные катушки: преимущества и примеры использования
Планарные катушки названы так из-за того, что все их части (витки) находятся практически на одной плоскости (т. е. они почти плоские). Они занимают намного меньше места, чем другие индукторы, и поэтому подходят для любых практических приложений с ограничениями по размерам, что очень актуально, к примеру, в микроэлектромеханических системах (МЭМС) или в имплантированных медицинских устройствах, например, сердечных насосах. Такие катушки могут изготавливаться как на жестких, так и на упругих подложках, и следовательно могут быть интегрированы как на классические печатные платы, так и на элементы для т.н. гибкой электроники. Планарные катушки также могут изготавливаться серийно, что является экономически выгодным.
Благодаря этим качествам, планарные катушки находят применение в различных областях, в основном, в высокочастотных приложениях. Некоторые примеры использования:
- Дистанционный мониторинг состояния здоровья (например, датчики кровяного давления)
- Беспроводная передача энергии (например, носимые/имплантируемые медицинские устройства)
- Радиочастотная идентификация (например, платежные карты)
- Индукционный нагрев (например, индукционные варочные панели)
Планарные катушки могут использоваться на печатных платах в портативных устройствах типа фитнес-трекеров.
В контексте разработки и проектирования планарных катушек наиболее важные характеристики — это индуктивность и сопротивление. Последнее определенно должно быть очень низким (в идеальном случае нулевым), так как любое сопротивление уменьшает эффективность катушки. Индуктивность, напротив, для эффективной связи с другими системами должна быть высокой. Определение сопротивления и индуктивности может являться достаточно сложной задачей, так как необходимо учитывать материал катушки, количество витков, связь между электрическими и магнитными полями.
Инженеры могут получить данные о сопротивлении и индуктивности планарных катушек на печатных платах численно, используя возможности модуля AC/DC для электромагнитных расчетов, являющегося расширением пакета COMSOL Multiphysics. Это модуль содержит в числе прочих физический интерфейс Electric Currents, Layered Shell (Электрические токи в многослойных оболочках), который позволяет эффективно описывать и моделировать в т.ч. конструкции плоских катушек. В качестве примера давайте рассмотрим простую модель планарной катушки.
Представление планарной катушки как многослойной оболочки с помощью модуля AC/DC
Модель представляет собой медную катушку, размещенную на печатной плате. Катушка содержит три витка, два межслойных соединения (перемычки), два контакта-терминала, один из которых служит источником тока, а второй заземлён. Ток с терминала начинает течь по верхнему слою. Затем он переходит по соединительной перемычке (via) на нижний слой, далее – по нему под витками, обратно на верхний слой по второй перемычке (via), и, наконец, проходит по всем виткам к контакту заземления. Протекая по катушке, ток индуцирует магнитное поле, причем отношение тока к магнитному полю как раз определяет индуктивность.
Геометрия планарной катушки, цветом на изображении показано распределение электрического потенциала.
Так как медная катушка является очень тонкой (толщина 0.1 мм, длина и ширина 0.5 мм), её предпочтительней моделировать в качестве граничного, а не объёмного компонента. Для того, чтобы описать топологию катушки в плоскости можно воспользоваться функционалом физического интерфейса Electric Currents, Layered Shell, который доступен с версии 5.4 программного обеспечения COMSOL®. К тому же, данный интерфейс можно использовать совместно с физическим интерфейсом Magnetic Fields (Магнитные поля), что позволит провести анализ растекания токов, генерации магнитных полей и, следовательно, вычислить не только сопротивление, но и индуктивность катушки. Процесс такого совместного расчета будет состоять из двух этапов:
- В рамках физического интерфейса Electric Currents, Layered Shell проводится расчёт как сосредоточенного сопротивления, так и поверхностной плотности тока в области катушки. Собственно данный интерфейс и предназначен для решения закона сохранения тока, протекающего по двумерному слою.
- Физический интерфейс Magnetic Fields затем использует рассчитанную в интерфейсе Electric Currents, Layered Shell поверхностную плотность тока для расчёта распределения магнитного поля вокруг катушки.
Не смотря на то, что конкретно этот пример довольно простой, вы можете использовать точно такой же подход для других более сложных геометрий и постановок. Чтобы узнать все детали и настройки выполненные при моделировании, ознакомьтесь с учебным примером Planar PCB Coil. По ссылке вы найдёте pdf-файл с пошаговыми инструкциями по сборке. А если у вас есть действующая лицензия, то сможете скачать и соответствующий MPH-файл модели.
Визуализация результатов электромагнитного расчета
После проведения расчета в результатах автоматически сгенерируются дефолтные графики с наиболее характерными визуализациями и величинами. В данной модели выведены графики распределения электрического потенциала (показан выше), а также магнитного поля, которое создаётся током, протекающим по катушке (показано ниже). В дополнение к графическим результатам, также можно рассчитать числовые выражения, в т.ч. на основе классических формул. В нашем случае, проведен расчет сопротивления и индуктивности. Для рассмотренной конструкции индуктивность равна 0.06 мкГн, а сопротивление — 21.6 мОм.
Распределение магнитной индукции вокруг катушки (цветом) и плотность тока (стрелки).
В данном примере мы продемонстрировали преимущества использования технологии по заданию многослойных оболочек в модуле AC/DC. С её помощью легко реализовать модель планарной катушки и определить сосредоточенные параметры — сопротивление и индуктивность. Используя расчетные данные, инженеры могут проводить оптимизацию топологий катушек для определенных сфер применения, например, добавляя больше витков для увеличения индуктивности. Результаты расчета предсказывают увеличение индуктивности с 0.06 мкГн до 0.11 мкГн при добавлении 4го витка.
Сравнение сопротивления и индуктивности для катушек с тремя и четырьмя витками. Визуализация распределения магнитной индукции приведена для случая четырёхвитковой катушки.
Дальнейшие шаги
Поработайте самостоятельно с рассмотренным примером расчета планарной катушки на печатной плате. По нажатию на кнопку вы перейдете в Библиотеку моделей и приложений (Application Gallery,), в которой сможете загрузить MPH-файл и документацию к рассмотренной модели.
Дополнительные материалы
Программы для расчетов цепей и узлов . Путеводитель в мир электроники. Книга 2
Работая над решением задачи, всегда полезно знать ответ.
Правило точности
RLC-цепи и элементы
Радио-калькулятор позволяет быстро определить:
• общее сопротивление при параллельном включении резисторов;
• реактивное сопротивление конденсатора на заданной частоте;
• реактивное сопротивление катушки индуктивности;
• резонансную частоту контура по известным L и С;
• количество витков однослойной катушки для заданной индуктивности;
• количество витков многослойной катушки;
• номиналы элементов для аттенюатора мостового типа;
• номиналы элементов для аттенюаторов Т и Н типа.
Выполнена в виде Web-страницы (все файлы программы занимают 26 Кб), автор Harry Lythall.
Расчет колебательного контура — простая программа для быстрого расчета параметров колебательного контура в разных вариантах. Здесь же можно рассчитать параметры однослойной катушки с нужной индуктивностью.
Написана под Windows и инсталляции не требует (kontur32.exe 259 Кб). Автор К. Гранкин.
Capacitor Calculator — радиотехнический калькулятор для определения параметров параллельного или последовательного включения до 5 разных конденсаторов и постоянной времени RC-цепи.
Работает из Windows и инсталляции не требует (файл самораспаковывающего архива ccalc.exe занимает 118 Кб).
Расчет трансформаторов и дросселей
Почти в любом радиотехническом устройстве имеется трансформатор. Не всегда удается купить такое изделие с нужными параметрами. В этом случае соответствующие программы позволяют быстро выполнить расчет таких узлов для необходимых значений напряжения и тока в нагрузке. Вот некоторые из них.
Transss! — программа для упрощенного расчета сетевого (220 В, 50 Гц) трансформатора с Ш-образным магнитопроводом. Вводится входное напряжение, необходимое выходное на нагрузке (после выпрямительного моста в пределе 3…130 В) и ток в нагрузке (в интервале 0,1… 1 А). Все остальное (число витков и диаметр провода для каждой из обмоток, мощность трансформатора, площади сердечника и окна) вычисляется автоматически. Работает из Windows, и инсталляция не требуется (transss.exe 34 Кб).
TR — позволяет выполнить расчет трансформатора или дросселя. Знает разные виды магнитопроводов. Работает из Windows, и инсталляции не требуется (все файлы занимают 335 Кб).
Программы для аналоговых таймеров
Довольно широко используются в разных конструкциях аналоговые таймеры из серии 555 (отечественный аналог К1006ВИ1). Выполняющие расчет временных параметров таких узлов, имеется много разных вспомогательных программ для персонального компьютера (вы их найдете на компакт-диске). Здесь Мы отметим только две. Пользоваться ими довольно просто: после запуска выбираем режим генератора (Astable) или одновибратора (Monostable) и вводим исходные значения времязадающих элементов. После этого сразу получаем рассчитанную частоту для генератора, собранного по типовой схеме (дополнительно еще может показываться рассчитанная длительность импульса (Т1) и рабочий цикл «duty cycle» — D = Т1/Т), а для одновибратора — только длительность импульса.
555 timer component selection — удобная программа, которая, в отличие от остальных, позволяет сразу выбирать номиналы времязадающей цепи из стандартного ряда (Е24) для элементов. Значения при расчете могут использоваться для резисторов от 1 кОм до 1 МОм, конденсаторов от 1000 пФ до 1000 мкФ. Правда, программа вас предупредить, что использовать конденсаторы с емкостью более 100 мкФ не рекомендуется (для микросхем, выполненных по биполярной технологии), но расчет все равно выполнит. Написана для Windows 95, 98 и не требует инсталляции (файл ic_555 занимает 221 Кб).
555 TIMER — программа позволяет рассчитать частоту автогенератора. При этом параметры резисторов можно вводить любые в интервале от 100 Ом до 10 МОм, а емкость от 100 пФ до 1 Ф. Написана для DOS (инсталляция не требуется), но работает и в Windows 95, 98 в режиме эмуляции DOS (весь комплект файлов занимает 215 Кб).
Существует много программ расчета, выполненных в виде HTML-документов (интернетовских страниц). Для их независимого использования (без подключения к Интернету) необходимо их переписать, сохранить на своем компьютере, перейдя. к меню «Добавить в избранное», отметив галочкой опцию «Сделать доступной автономно». Варианты таких программ и обучающую информацию по практическому использованию таймеров вы сможете найти в Интернете по адресам:
http://webhome.idirect.com/~jadams/electronics/555calcs.htm
http://www.hot.ee/ps00/ele/555.htm
http://www.ilmu.8k.com/kalkulator/kal555.html
http://www.westminster.org.uk/intranet/departments/electronics/555.htm
http://www.williamson-labs.com/555-circuits.htm
http://ourworId.compuserve.com/homepages/Bill_Bowden
Расчет индуктивности на феррите
Калькулятор обновлен 04.12.2017. Не забудьте обновить кэш браузера (Ctr+F5). Калькулятор имеет следующие ограничения в расчетах:
- шаг намотки не может превышать удвоенного диаметра провода;
- диаметр катушки не может быть больше удвоенного диаметра стержня;
- длина намотки должна быть меньше 3/4 длины стержня;
- при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
- начальная магнитная проницаемость стержня должна быть больше 100;
Расчет катушки на ферритовом стержне:
ВВЕДИТЕ ИСХОДНЫЕ ДАННЫЕ:
| L | = | – требуемая индуктивность |
Параметры ферритового стержня:
| lf = | – Длина стержня |
| df = | – Диаметр стержня |
| µ = | – Начальная магнитная проницаемость |
Параметры катушки:
| dc = | – Диаметр каркаса |
| s = | – Смещение от центра стержня |
| dw = | – Диаметр провода |
| p = | – Шаг намотки |
РЕЗУЛЬТАТ:
| N = | – Число витков |
| µэфф = | – Эффективная магнитная проницаемость стержня |
| lc = | – Длина намотки |
Первые 12 комментариев относятся к старой версии калькулятора, основанной на другой методике расчета. С формулами и методом расчета можно ознакомиться здесь.
Калькулятор обновлен 04.12.2017. Не забудьте обновить кэш браузера (Ctr+F5). Калькулятор имеет следующие ограничения в расчетах:
- шаг намотки не может превышать удвоенного диаметра провода;
- диаметр катушки не может быть больше удвоенного диаметра стержня;
- длина намотки должна быть меньше 3/4 длины стержня;
- при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
- начальная магнитная проницаемость стержня должна быть больше 100;
Расчет катушки на ферритовом стержне:
ВВЕДИТЕ ИСХОДНЫЕ ДАННЫЕ:
| L | = | – требуемая индуктивность |
Параметры ферритового стержня:
| lf = | – Длина стержня |
| df = | – Диаметр стержня |
| µ = | – Начальная магнитная проницаемость |
Параметры катушки:
| dc = | – Диаметр каркаса |
| s = | – Смещение от центра стержня |
| dw = | – Диаметр провода |
| p = | – Шаг намотки |
РЕЗУЛЬТАТ:
| N = | – Число витков |
| µэфф = | – Эффективная магнитная проницаемость стержня |
| lc = | – Длина намотки |
Первые 12 комментариев относятся к старой версии калькулятора, основанной на другой методике расчета. С формулами и методом расчета можно ознакомиться здесь.
В отличии от тороидальной индуктивности на ферритовом кольце, магнитный поток катушки на ферритовом стержне не замкнут целиком внутри феррита и каждая силовая линия проходит и по ферритовому стержню и по воздуху, поэтому расчет такой катушки представляет довольно сложную задачу. Индуктивность зависит от:
- магнитной проницаемости ферритового стержня и его размеров;
- размеров самой катушки;
- взаимного соотношения размеров катушки и стержня;
- положения катушки относительно центра стержня.
Расчет индуктивности катушки на ферритовом стержне основан на определении относительной эффективной проницаемости стержня. Другими словами, нам нужно определить насколько возрастет индуктивность катушки с “воздушным сердечником” если внутрь нее вставить ферритовый стержень. Основная формула выглядит вот так:
| μe = Lf / Lair = (1 + x) / (1 / k + x / μfe ) | [1] |
,где Lf / Lair — отношение индуктивности катушки с ферритом к индуктивности той же катушки без феррита, а коэффициенты x, k и μfe вычисляются по следующему алгоритму:
где ε0 = 8,8542*10 -12 Ф/м — электрическая постоянная, μ — начальная магнитная проницаемость материала стержня. Основные размеры в метрах, обозначения понятны из рисунка:
Немного теории обосновывающей этот алгоритм.
- Можно считать что воздушная катушка имеет магнитную цепь состоящую из двух частей. Снаружи катушки и внутри нее. Они отличаются плотностью силовых линий и магнитным сопротивлением . Если магнитное сопротивление внутренней части магнитной цепи выше, чем наружной части (а это так, поскольку ее площадь поперечного сечения намного меньше), тогда применение феррита уменьшает это сопротивление и имеет эффект увеличения индуктивности. Это отношение двух частей магнитных сопротивлений магнитной цепи воздушной катушки обозначено в основной формуле как x и вычисляется на 5-ом шагу алгоритма.
- Параметр μfe учитывает случай, когда обмотка не плотно прилегает к стержню, т.е. между стержнем и обмоткой существует радиальный зазор.
- Параметр Canf учитывает влияние частей стержня, которые выступают за пределы катушки. Эти части уменьшают магнитное сопротивление внешней части магнитной цепи и также увеличивают индуктивность.
- Параметр φ_φmax учитывает конечное магнитное сопротивление феррита. Этот параметр, наряду с параметром Canf используется для расчета коэффициента k из основного уравнения [1]
При смещении катушки относительно стержня индуктивность катушки уменьшается, это обстоятельство учитывается с помощью поправочного коэффициента K:
| K = -440.9943706*sh 8 +1318.707293*sh 7 -1604.5491034*sh 6 +1021.078226*sh 5 -363.8218957*sh 4 +71.6178135*sh 3 -7.6027344*sh 2 +0.3013663*sh+0.995 | [2] |
- sh — относительное смещение = смещение s деленное на половину длины сердечника [sh = s / ( lf / 2 )].
Эта формула получена методом регрессионного анализа и справедлива при s = 0,05 — 0,75
В итоге индуктивность катушки на ферритовом стержне определяется по следующей формуле:
| L(мкГн) = μe Lair*K | [3] |
Индуктивность катушки “воздушным” сердечником Lair рассчитывается по алгоритму расчета однослойной катушки с учетом шага намотки. Длину намотки можно определить по следующей формуле:
- N — число витков.
- dw — диаметр провода.
- p — шаг намотки.
Алгоритм имеет следующие ограничения в расчетах:
- шаг намотки не может превышать удвоенного диаметра провода;
- диаметр катушки не может быть больше удвоенного диаметра стержня;
- длина намотки должна быть меньше 3/4 длины стержня;
- длина стержня должна быть не менее чем в 12 раз больше его диаметра;
- при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
- начальная магнитная проницаемость стержня должна быть больше 100;
Также как и в дросселе на ферритовом кольце с немагнитным зазором, при больших значениях начальной магнитной проницаемости стержня его эффективная магнитная проницаемость слабо зависит от начальной и составляет величину не более нескольких десятков.
В версиях плагина ferrite.coi ниже 0.3 использовалась методика расчета, предложенная В.И. Хомичем в книге “Ферритовые антенны МБР-721 1989г.” Как оказалось, эта методика дает ошибочный результат расчета. В плагине версии от 0.3 до 11.2 применялась методика по ссылке [2]. Эта методика также не согласуется с реальными измерениями. Расчет изложенный в этой статье основан на работе Алана Пейна G3RBJ (см ссылку [1]). Расчет идет по формулам [1],[2], [3] и [4] методом итераций. Расчет реализован в плагине версии 12.2 и выше.
Особая благодарность Андрею Васильевичу Каинову за конструктивную помощь и соавторство в разработке методики расчета.
Coil32 – Калькулятор однослойной катушки
- Детали
- Просмотров: 20117
Вы должны включить JavaScript в вашем браузере, чтобы калькулятор работал на этой странице!
Расчет однослойной катушки индуктивности:
Если вам нужно сделать катушку индуктивности для согласующей цепи, для усилителя, для радиоприемника Magic Crystal и т. Д., У вас есть вопрос:
- сколько витков у катушки
- какой диаметр и длина намотки
- какой провод нужен для использования
Конструкцию обмотки следует выбирать опытным путем, следуя следующим общим советам.Большинство онлайн-калькуляторов позволяют найти индуктивность катушки, зная размеры ее намотки и количество витков. Этот калькулятор поможет вам оценить количество оборотов однослойного R.F. индуктор или дроссель на стадии проектирования. В калькуляторе используется уравнение Боба Уивера с поправками на круглую проволоку. Coil32 for Windows и кроссплатформенная Coil64 позволяют рассчитать собственную емкость и добротность однослойной катушки.
Рассчитать количество оборотов
ВВЕДИТЕ ВХОДНЫЕ ДАННЫЕ:
| Выберите единицы: | мм / см / дюйм | AWG → 000000000012345678910111213141516171819202122232425262728293031323334353637383940 | SWG → 07.06.05.04.03.02/001234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950 |
Coil64 также оценивает добротность и собственную емкость однослойной ВЧ-катушки.
Ниже приведены ссылки на лучшие, на мой взгляд, онлайн-калькуляторы, позволяющие найти индуктивность готовой катушки индуктивности.
Артикул:
- Калькулятор индуктивности однослойной катушки от IN3OTD
- Калькулятор индуктивности RF от ON4AA
- Калькулятор индуктивности круглой катушки от R.Weaver
Подробнее о индукторах с воздушным сердечником Преимущества катушки с воздушным сердечником: И “обратная сторона”: |
Расчет конструкции индуктора с однослойным воздушным сердечником • Схемы
информация Намотка провода в один слой дает индуктивность с минимальной паразитной емкостью и, следовательно, дает максимально возможную собственную резонансную частоту (SRF). Стремление получить высокий SRF и низкие потери является ключом к созданию катушек, которые обладают радиочастотными свойствами, имеющими некоторое полезное сходство с чистой индуктивностью.
Расчет основан на формуле Уиллера 1928 года для однослойного соленоида, которая в исходной форме представлена как:
L = a² N² / (9a + 10b), [микрогенри], b> 0.-7 Н² (a² / b) / (1 + 0,45 (D / l)) [Генри]
где ..
- L – индуктивность по Генри
- D – диаметр рулона в метрах
- r – радиус в метрах (или D / 2)
- л – длина змеевика в метрах
- N – количество витков
Обратите внимание, что точность этой формулы составляет ± 0,33%, если отношение D / l> 0,4. так что эта формула лучше всего подходит для длинных соленоидов.
Примечание: Эта формула применяется на «низких» частотах (<3 МГц) при использовании эмалированной медной проволоки (магнитной проволоки) с закрытой намоткой.
Совет 1 Незначительное уменьшение индуктивности может быть достигнуто путем небольшого разведения витков. Это также уменьшит саморезонанс. Можно попробовать другие комбинации диаметра проволоки и катушки, но наилучшие результаты обычно достигаются, когда длина катушки равна ее диаметру.
Совет 2 Если вам нужна хорошая индукционная стабильность при наличии вибрации, намотайте катушку на подставку из подходящего немагнитного пластика или керамического каркаса и зафиксируйте обмотки с помощью эпоксидного клея или другого подходящего клея.
Расчет индуктивности
В этом калькуляторе индуктивности однослойной катушки используется формула Лундина [5], для которой максимальная относительная погрешность составляет менее 3 ppm.
Значение Q вычисляется здесь по формуле из [6]; значение будет лишь приблизительной оценкой; кроме того, не учитывается влияние распределенной емкости змеевика.
Большинство формул для индуктивности катушки действительны для приближения токового слоя , где ток течет по бесконечно тонкой поверхности вокруг диаметра катушки.Это то же самое, что предположить, что катушка намотана бесконечно тонкой лентой с незначительным расстоянием между витками. Если расстояние между витками невелико, следует применить поправочный коэффициент. Более того, на высоких частотах ток течет внутрь катушки, поэтому эффективный радиус, по которому протекает ток, становится меньше. Иногда предлагается использовать в расчетах внутренний радиус катушки вместо среднего радиуса проволоки, чтобы компенсировать этот эффект.Однако разница между низко- и высокочастотной индуктивностями обычно невелика [1].
Для точного вычисления индуктивности любого типа катушки (или также более сложных проводящих структур) необходимо использовать электромагнитный симулятор.
Что касается формул индуктивности токового слоя для однослойных катушек, одна из наиболее широко известных – это формула Уиллера [2], которая утверждает (после преобразования в метрические единицы):
L = (d 2 n 2 ) / (l + 0.45d) [мкГн]
где d – диаметр катушки в метрах, n – количество витков, l – длина катушки в метрах.
Приведенная выше формула имеет точность в пределах 1% для l> 0,4d; для более коротких катушек можно использовать хорошо известную формулу Нагаока [3] (неудобство которой состоит в том, что требуется список табличных значений для различных соотношений диаметра / длины) или другие асимптотические приближения [4].
Некоторые полезные формулы, применимые для любого отношения диаметра к длине, представлены в [4] и [5];
Артикул:
| [1] | F.Э. Терман, “ Справочник радиоинженера “, Лондон, МакГроу-Хилл, 1-е изд., Сентябрь 1950 г. |
| [2] | Х.А. Уиллер, “ Простые формулы индуктивности для радиокатушек “, Proc. I.R.E. , т. 16, стр. 1398-1400, октябрь 1928. |
| [3] | H. Nagaoka, “ Коэффициенты индуктивности соленоидов “, J. Coll. Sci. , т. 27, стр. 18-33, 1909. |
| [4] | Х.А. Уиллер, “Формулы индуктивности для круглых и квадратных катушек “, Proc.IEEE , т. 70, нет. 12, pp. 1449-1450, декабрь 1982 г. |
| [5] | R. Lundin, “ Справочная формула для индуктивности однослойной круговой катушки “, Proc. IEEE , т. 73, нет. 9, pp. 1428–1429, сентябрь 1985 г. |
| [6] | Ф. Лэнгфорд-Смит (редактор), “ Справочник разработчика радиотронов “, 4-е издание, Австралия, Wireless Press, 1952 г. |
Ссылки на моталки Страница
К4ЗАД своими руками Калькулятор намотки катушки Ссылки
Радио домашние пивовары легко справляются с работой с резисторами и конденсаторами; они поставляются в аккуратных маленьких упаковках, и их ценность легко решительно, но работать с индукторами не так просто.Чтобы получить индуктивность и другие желаемые характеристики, катушки часто не могут быть куплены и должны быть намотаны на заказ. Катушка дизайн / создание включает в себя выбор правильной формы катушки, размера провода и материал сердечника (если не воздух), все составляющие процесс немного сложный. к счастью несколько авторы / веб-программисты взяли основные формулы для конструкции индуктора и создали онлайн-калькуляторы, помогающие определить физический параметры, необходимые для катушки с желаемой электрической характеристики.Ниже приведены ссылки на онлайн-калькуляторы. полезен при разработке катушек для радиоприложений. Смотреть на этих сайтах, так как некоторые из них перечисляют другие полезные калькуляторы.
Кому насколько мне известно во время создание этой страницы все ссылки к бесплатным калькуляторам без регистрации, необходимой для использования. Как и я использовал только некоторые из них я не давать никаких рекомендаций, и порядок листинга не указывает предпочтение. Информация о каждом может помочь вам выбрать лучшие удовлетворяя ваши потребности.Стоит отметить, что авторы некоторых критически относятся к точности используемых формул другими.
Многие благодаря авторам за их работу в создание этого браузерного дизайна вспомогательные средства доступны.
### Указывает на калькуляторы которые выходят за рамки простого решения уравнения для одного заявленного отсутствующее значение, найдя недостающее значение при условии, что другие значения введены.
Несколько Расчеты или конфигурации катушек:
Три
Калькуляторы индуктивности – Единицы: nHenrys, uHenrys
& mHenrys – Вычисляет количество витков катушки AL и L
Индуктивность и многое другое
– Несколько вариантов единиц измерения – Выходная индуктивность – Калькуляторы для
доступно несколько форм без катушки.
Калькулятор индуктивности катушки –
Несколько
выбор единиц – вычисляет индуктивность для однослойных / многослойных соленоидов
и плоские спиральные катушки
Найти
L для катушек и других форм
– Несколько вариантов юнитов +
Проницаемость – Выходная индуктивность
Калькулятор индуктивности с двумя катушками –
Входы в дюймах – Делает однослойные и многорядные многослойные
катушки.Вычисляет L
Пять
Калькуляторы катушки / индуктивности
– Несколько калькуляторов индуктивности
использование различных знаний для входных данных – Размеры в мм
Три катушки / калькуляторы индуктивности
– Вводятся в см или дюймах – Делает однослойный
и многорядные многослойные катушки.
Вычисляет L
Три калькулятора катушек / индуктивностей
– Выбор единиц для входов – 2 выхода – индуктивность –
другое – реактивность
Одноместный Катушки с воздушным сердечником слоя:
Калькулятор индуктивности с воздушным сердечником
– Широкий выбор единиц размера катушки – Вычисляет индуктивность с выбором
единицы
Воздух
Конструктор сердечника индуктивности – Калькулятор – Ввод
в миллигенах и дюймах – расширенный вывод на новую страницу
Калькулятор индуктора с воздушным сердечником
– включает Q
– Размеры в мм – Вычисляет
Индуктивность, добротность и длина провода
AL Калькулятор индуктивности ###
– Введите два значения и получите третье – Единицы индуктивности:
mHenrys, uHenrys, nHenrys
Калькулятор индуктивности катушки
– Размеры в дюймах
-Вычисляет индуктивность в uHenrys
и длина провода в дюймах и футах
Калькулятор с двумя катушками
– Входные размеры в миллиметрах или дюймах и количество оборотов – Вычисляет индуктивность и
количество витков
Helical Coil Calculator – Input
размер в мм или дюймах – вычисляет индуктивность и провод
длина – включает
собственная емкость
Многоступенчатая конструкция катушки
-Входной размер в мм – Расчеты для
несколько свойств змеевика – с примерами
LF
Калькулятор индуктивности
– Размеры в мМетрах и МГц (для Q)
– Результат в microHenrys и Q
Одноместный
Слой, воздушный сердечник, калькулятор индуктивности – размеры указаны в
мм МГц (для Q)
– Вычисляет L в нескольких единицах измерения и длине провода
Калькулятор индуктивности воздушного сердечника
–
Размеры в дюймах – Выход в
uHenrys
Индуктивность
однослойных катушек на
цилиндрические формы – введите радиус, длину, проницаемость
и количество витков – вычисляет калькуляторы индуктивности uH
LC
– Входные витки, диаметры катушек и проводов в дюймах –
Вычисляет uHenrys и провод и катушку
длина
Калькулятор индуктивности катушки с воздушным сердечником
– Входные обороты, диаметр и длина рулона в дюймах – Расчет L в
uHenrys
Однослойный
Калькулятор воздушной катушки
– Широкий выбор единиц – Входная длина, диаметры катушек и проводов – Вычисления
Обороты и длина рулона
Одноместный
Калькулятор слоев воздушного змеевика – ###
–
Поля ввода – обороты, диаметр, длина и L – введите 3, получите 4-е.-
С примерами
Еще одна однослойная воздушная катушка
Калькулятор
– Выбор единиц – Входная длина, диаметры катушки и проволоки – Вычисление оборотов
и длина рулона
Калькулятор цилиндрической катушки профессора Койла
– Закрывает ли катушки намотки и намотки пространства – Прочтите инструкции
первый
Два
Калькуляторы катушек – выбор
единиц – один рассчитывает L, другой витки и длину намотки
Одноместный Слой катушек поверх магнитного материала:
Универсальный однослойный калькулятор –
###
–
Ввод: 4 параметра и 5-й – банка
использоваться для поиска неизвестного ядра
Проницаемость
Комплексный
Калькулятор катушки
– Слишком обширно, чтобы резюмировать – Взгляните на это –
Включает в себя
собственная емкость
Конструкция катушки
и калькулятор индуктивности
– Ввод: размеры в метрических единицах или дюймах – Вычисляет индуктивность
в uHenrys
Индуктивность
однослойных катушек – вход:
Обороты, размеры в мметрах и перм.- Вычисляет L на новой странице
вычисляет индуктивность круговой петли
–
Ввод: витки, размеры в миллиметрах и перми. – Рассчитывает L в
Генри
находит индуктивность однооборотного соленоида
–
Выбор единиц измерения – Ввод: число оборотов, радиус длины и допустимость. – Выход
L
в нескольких единицах
Цилиндрическая катушка индуктивности
Калькулятор дизайна –
### – с помощью
4 калькулятора – выбор
единиц –
Вычисляет L, повороты, допуск, площадь и длину
Тороид Катушки:
Калькулятор тороида амидона (железный порошок)
– Введите желаемый размер ядра uHenrys и Amidon и цвет в
найти L, повороты и т. д.
Калькулятор тороида Amidon (феррит)
– Введите желаемый размер ядра uHenrys и Amidon и цвет в
найти L, повороты и т. д.
Калькулятор индуктивности с ферритовым сердечником
–
Введите количество витков и AL, чтобы найти индуктивность катушки.
Индуктивность тороида – Вход
размеры сердечника в см, количество витков и проницаемость для поиска катушки
Индуктивность
Калькулятор индуктивности тороида
– Вход
размеры сердечника в мм или мил, количество витков
и проницаемость, чтобы найти катушку
Индуктивность
Калькулятор индуктивности тороида на оборот
– Широкий выбор единиц ввода и количества оборотов –
Выходы L и другие характеристики
Калькулятор с двумя тороидальными индукторами
– Широкий выбор устройств ввода / вывода
& количество витков – Выходы L
и другие характеристики
Калькулятор намотки тороида –
Находит количество витков для питаемых железных и ферритовых сердечников.
известный размер и состав материала
Некоторые
Справка по работе с тороидами: (См. Также
последний
раздел Дополнительные
Катушка
Информация ниже)
Тороид
Таблица спецификаций – для тороидов 88 – с гибким
калькулятор
Toroid
Графики характеристик – Восемь диаграмм данных по тороидам
G-QRP
Информация о клубном тороиде – для обычных тороидов – включает AL
данные
Таблица индуктивности тороида
G-QRP Club
– PDF-файл значений mHenrys для
много цветов
тороиды
с 1-50 оборотами
Что это за материал? – Мой PDF
Сборник (Скачать) методов идентификации материала тороида
Калькулятор индуктивности тороидального сердечника Ferrte
– Мощный автономный калькулятор Excel с числовыми и
графические результаты.
Тороиды – некоторые практические соображения
– Подробная статья – с номинальной мощностью (Ватт) для многих
общие тороиды
Собственная емкость
Тороида
Индукторы – возможно, больше, чем вам нужно знать.
собственная емкость в конструкции катушки
Спираль (Плоские) Катушки
Плоские спиральные индукторы с воздушным сердечником
– Большой выбор единиц измерения – Находит индуктивность – Пять других
калькуляторы катушек здесь
Flat Spiral Coil Calculator –
Принимает вводимые размеры в дюймах или мм – вывод в uHenrys
Плоская спиральная катушка
Калькулятор индуктивности
– Размеры в мкм – Имеет несколько плоских форм – Другое
калькулятор ссылки здесь
Однослойный
Калькулятор плоской воздушной катушки – принимает
вводимые размеры в дюймах или мм – вывод в uHenrys или nHenrys
Спираль
Калькулятор индуктивности
– Размеры в мметрах – Девять
выходы, для различных форм и формул, рассчитываются
Калькулятор спиральной катушки
– Габаритные размеры
в мм и количество оборотов – Выход
в uHenrys – Использует формулу Уиллера
Калькулятор спирали профессора Койла из паутины
– Красиво – Включает в себя таблицу проводов и калькулятор резонанса – Прочтите
инструкции ниже
Соленоид – Многослойные катушки:
Многослойный
Калькулятор индуктивности с воздушным сердечником
– Выбор единиц – Входы: L, Катушка
диаметр и длина, калибр провода – несколько выходов
Многослойный
Калькулятор индуктивности воздушного сердечника
– Выбор единиц – Сложные входы из-за слоев – Только полезные
ниже 3 МГц
Калькулятор индуктивности многослойной катушки
–
Air Core – мм или дюймы – сложные входы
из-за слоев – Несколько выходов
Калькулятор физических свойств катушки
– Для катушек соленоидов реле – Не для RF
Проницаемость – Найди Проходимость неизвестного керна
Определите проницаемость тороида
– Вводятся в mHenrys
к nHenrys и мм
или
см размеры жилы – Выпуск Пермь.& AL
Как определить проницаемость неизвестного
Ядра – Входы в uHenrys
& размеры в мм – Также калькулятор индуктивности
Видеть
также: Универсальный однослойный калькулятор ###
Реактивное сопротивление:
Калькулятор индуктивного сопротивления –
Принимает входные данные в герцах до ГГц и от нГенри до Генри.
Калькулятор импеданса индуктора
– Принимает входные сигналы в герцах до МГц и
Калькулятор реактивного сопротивления от pHenrys до Henrys
R L C
###
– Единицы
исправлены: uFarads, mHenrys & Hertz – Ссылки на
емкостной
Калькулятор реактивного сопротивления
Реактивное сопротивление
Калькулятор для обоих аккредитивов
-& Единицы
фиксированы: pFarads, uHenrys и MHz
Другой Калькуляторы:
Калькулятор взаимной индуктивности –
Вычисляет взаимную индуктивность с учетом индуктивности 2 катушек (в
mHenrys) и их коэффициент связи.
Другой калькулятор взаимной индуктивности
– То же, что и выше, но предлагает выбор единиц.
Сайт разработки радиочастотных фильтров WA4DSY
– Есть несколько типов фильтров с выходными графиками – Действительно
полезный; a keeper
Калькулятор коэффициента поворотов –
Возводит ли отношение поворотов в квадрат. Калькулятор глубины кожи
RF Cafe –
Нечасто требуется, но с отличного сайта для радиотехников и радиолюбителей. Калькулятор самоиндукции провода
–
Выбор входных единиц – вычисляет L в нГенри
длина провода
Комплексная конструкция катушки Тесла –
Нет
полезно для РФ?
Подробнее
Калькуляторы катушки Тесла
– Не подходит для РФ
Дополнительно Информация о катушке:
Балун
и выбор сердечника трансформатора – много полезной информации и
ссылки из W8JI
Проволока,
Тороиды и трансформаторы
– много полезного
информация – Включает таблицу сечения проводов и многое другое.
PDF – Измерение свойств мягкого ферритового сердечника
– Четырехстраничный PDF-файл с информацией об измерениях.
Все о феррите из гаек
& Volts Magazine – Хорошее образование со ссылками
в конце
### калькуляторы которые выходят за рамки простого решения уравнения для одного заявленного отсутствующее значение, найдя недостающее значение при условии, что другие значения введены.
Пожалуйста контакт мне о других приложениях этого типа и о любые исправления информации на этой странице.
Назад к странице указателя
Основной
Сайт – Архив истории морского радио
Создано 11.11.2018 – Доработка 19.07.2021
Как рассчитать индуктивность катушки (однослойные индукторы с цилиндрическим сердечником)
Индуктивность катушки зависит от ее геометрических характеристик, количества витков и способа намотки катушки. Чем больше диаметр, длина и большее количество витков обмотки, тем больше ее индуктивность.
Если катушка намотана плотно, от поворота к витку, то она будет иметь большую индуктивность, чем катушка с неплотной намоткой, с промежутками между витками. Иногда вам нужно намотать катушку с заданной геометрией, а у вас нет проволоки с требуемым диаметром, тогда, если вы используете более толстую проволоку, вам следует немного увеличить количество витков, а если использовать более тонкую проволоку, это нужно для уменьшения количества витков катушки, чтобы получить требуемую индуктивность.
Все вышеперечисленное относится к обмоткам без ферритовых сердечников.
Индуктивность однослойных катушек на цилиндрических формах обмоток можно рассчитать по формуле:
L = ( D /10) 2 * n 2 /( 4.5 * D + 10 * l ) (1)
Где
L – индуктивность катушки, мкГн;
D – диаметр катушки (диаметр формовки), мм;
l – длина змеевика, мм;
n – количество витков обмоток.
В расчете может быть две задачи:
А. Приведена геометрия катушки, найти индуктивность;
В. Дана индуктивность катушки, посчитайте количество витков и диаметр провода.
В случае «А» все данные указаны, индуктивность найти несложно.
Пример 1. Рассчитаем индуктивность катушки, показанной на рисунке выше. Подставьте значения в формулу 1:
L = (18/10) 2 * 20 2 / (4.5 * 18 + 10 * 20) = 4,6 мкГн
Во втором случае известны диаметр катушки и длина намотки. Длина намотки зависит от количества витков и диаметра проволоки. Поэтому рекомендуется производить расчет именно в таком порядке. Исходя из геометрических соображений, определите размер катушки, диаметр и длину намотки, а затем подсчитайте количество витков по формуле:
n = 10 * (5 * L * (0,9 * D + 2 * L )) 1/2 / D (2)
После того, как вы нашли количество витков, определите диаметр провода с изоляцией по формуле:
d = l / n (3)
Где
d – диаметр проволоки, мм;
l – длина намотки, мм;
n – количество витков.
Пример 2. Нам нужно сделать катушку диаметром 10 мм и длиной обмотки 20 мм, катушка должна иметь индуктивность 0,8 мкГн. Обмотка однослойная, от поворота к повороту.
Подставляем значения в формулу 2, получаем:
n = 10 * (5 * 0,8 * (0,9 * 10 + 2 * 20)) 1/2 /10 = 14
Диаметр проволоки: d = 20/14 = 1,43 мм
Для намотки катушки проводом меньшего диаметра необходимо расположить полученные расчетным путем 14 витков по всей длине катушки (20 мм) с равными интервалами между витками (шаг намотки).Индуктивность катушки будет на 1-2% меньше номинальной, это следует учитывать при изготовлении этих катушек. Чтобы намотать катушку проволокой толще 1,43 мм, новый расчет следует производить с увеличенным диаметром или длиной обмотки катушки. Вам также может потребоваться увеличить диаметр и длину одновременно, пока не получите желаемые размеры катушки для данной индуктивности.
Следует отметить, что приведенные выше формулы предназначены для расчета катушек с длиной намотки l равной половине диаметра или более.Если длина намотки меньше половины диаметра намотки D /2, более точные результаты можно получить, используя следующие формулы:
L = (D /10) 2 * n 2 / ((4 D +11 l )) (4)
и
n = (10 L * (4 D +11 l )) 1/2 / D (5)
Артикул: «300 практических советов»
Датчики| Бесплатный полнотекстовый | Быстрый и точный инструмент для расчета самоиндуктивности многослойных плоских катушек
1.Введение
С годами наблюдается рост решений, основанных на технологиях с использованием плоских катушек [1,2]. Благодаря своим характеристикам изготовления и рабочим характеристикам, планарные катушки предлагают решения с меньшим весом, лучшей механической стабильностью и объемной эффективностью по сравнению с соленоидами, что позволяет использовать их в широком диапазоне приложений [2,3]. Кроме того, поскольку плоские катушки могут быть напечатаны на традиционных печатных платах (PCB) или на гибких материалах, таким образом может быть достигнуто воспроизводимое, предсказуемое и экономически эффективное производство, что упрощает процессы сборки и интеграции [4,5,6].Комбинация этого метода производства с высокой надежностью индуктивных технологий приводит к созданию решений, которые предлагают надежность, долговечность, хорошие тепловые характеристики, гибкую конструкцию, высокую репликационную способность для приложений во влажных и суровых условиях, таких как наличие масло и пыль [7,8]. Благодаря своим характеристикам и функциям планарные катушки на основе печатных плат отвечают многим требованиям, предъявляемым конкурентоспособными отраслями промышленности, такими как автомобилестроение, здравоохранение, робототехника, электроника, от маломощных до мощных приложений [9,10,11].В автомобильной промышленности плоские катушки широко используются, например, в электромобилях (EV) [12], благодаря интеграции систем беспроводной передачи энергии (WPT). Развитие этих систем будет способствовать совершенствованию процесса динамической беспроводной зарядки (DWC), устраняя некоторые из основных препятствий для внедрения электромобилей, связанных с управлением накопленной энергией, емкостью аккумулятора, временем зарядки и высокими затратами, связанными с этим. [12]. В производстве медицинских устройств плоские катушки также использовались для зарядки имплантируемых устройств [9,13].Это позволяет не только уменьшить размер имплантируемых устройств, поскольку требуются батареи меньшего размера, но также снижает потребность в хирургических операциях по замене и, как следствие, риск инфицирования пациента или повреждения органов или мышечных тканей. Планарные катушки также используются в различных измерительных приложениях из-за их способности удовлетворять ограничения, связанные с размером устройства, производственными затратами и суровыми условиями эксплуатации. В настоящее время на рынке уже есть датчики смещения и углового положения, которые объединяют плоские катушки в свой механизм преобразования, такие как вихретоковый эффект или индуктивная связь [2,14,15], например, безмагнитные индуктивные датчики положения IPS2200, производимые компанией Компания Renesas [16].Учитывая большой интерес нескольких отраслей промышленности к технологии планарных катушек и огромную конкуренцию на рынках, необходимо сократить цикл разработки новых устройств, чтобы идти в ногу с быстрыми темпами конкурентов [2]. Проектирование и оптимизация плоских катушек – сложный, дорогостоящий и трудоемкий процесс, обычно основанный на методах моделирования конечных элементов (МКЭ) и экспериментальных измерениях [17,18,19]. В литературе [1,8,20,21,22,23,24,25,26] также можно найти быстрые аналитические методы в закрытой форме для оптимизации катушек.Однако эти методы ограничиваются расчетом самоиндукции обычных катушек с определенной геометрией. В этой работе предлагается аналитический инструмент для расчета самоиндуктивности обычных многослойных планарных катушек, сочетающий в себе точность, универсальность и скорость. . Основная цель – улучшить и упростить процесс проектирования плоских катушек с минимальными вычислительными ресурсами, позволяя анализировать, как различные конструктивные параметры катушек (такие как количество витков, расстояние между витками, ширина витков, количество витков сегментов на оборот, а также внутренний и внешний диаметры) влияют на индуктивность катушки.Следующие разделы представляют и подтверждают предложенную аналитическую модель. В разделе 2 показаны аналитические выражения, обычно используемые для расчета самоиндукции планарных катушек, в разделе 3 подробно описан предлагаемый метод аналитического расчета планарных катушек, а в разделе 4 подтверждается валидация предложенной модели путем сравнения с моделированием МКЭ и экспериментальными измерениями. Для более полной проверки были использованы и проанализированы различные геометрии и размеры катушек. В разделе 5 делаются основные выводы валидации модели и обсуждается ее эффективность.2. Обзор аналитических моделей
В отличие от соленоидов, внутренняя площадь плоской катушки зависит от ее внешнего диаметра, количества витков, ширины провода и расстояния между витками. Таким образом, этот тип катушек отличается тем, что все витки имеют разную длину, и из-за этого расчет самоиндукции плоских катушек становится более сложным. Автоиндуктивность катушки зависит от взаимной индуктивности между каждым витком тока, самоиндукции провода катушки и окружающей среды.Принимая во внимание это, а также особенности плоских катушек, упомянутые ранее, становится очевидной сложность, связанная с расчетом автоиндуктивности для конструкции плоских катушек.
Согласно литературе [1,8,20,21,22,23,24,25,26,27,28,29], для определения конструкции катушки для приложения выделяются два типа методологий: численные методы, например метод конечных элементов (МКЭ), и формулы аппроксимации. Хотя моделирование методом конечных элементов является наиболее точной методологией, оно требует дорогостоящих программ моделирования, больших вычислительных ресурсов, а сама разработка модели конечных элементов представляет собой кропотливый и сложный процесс.Он также имеет недостаток, заключающийся в том, что моделирование модели может занимать от минут до нескольких часов или дней, в зависимости от сложности модели, желаемой точности и количества случаев и переменных в моделировании. Благодаря этим аспектам этот метод может стать более подходящим для верификации проекта, чем для его разработки [7]. Таким образом, методология, основанная на формулах аппроксимации, идеальна для преодоления части недостатков моделирования методом конечных элементов, поскольку больше не требуется использовать большие вычислительные ресурсы и специализированные программные инструменты.Эта методология заключается в применении выбранной формулы, замене переменных модели параметрами конструкции змеевика, и поэтому она намного быстрее по сравнению с полным моделированием МКЭ. Однако эта простота накладывает некоторые ограничения на геометрию катушки, к которой применяется аппроксимация, а также на точность результатов модели. Основываясь на литературе [1,8,20,21,22,23,24,25,26,30], существует несколько приближенных формул для расчета индуктивности планарных катушек, некоторые из которых зависят от конкретного применения [18,30,31, 32], или действительны только для одного типа геометрии, например, исследовательских работ Брайана, Термана, Оливея, Глисона, Дилла и других [1,26,33,34], некоторые остаются действительными для нескольких обычных геометрий, таких как Data Fitted Моном, приближение текущего листа и модифицированный Уиллер [1,24,26,35].Последние из-за их большей универсальности и точности результатов по сравнению с другими, предложенными в литературе, являются наиболее часто используемыми. Эти формулы аппроксимации были разработаны Mohan et al. [35] и утверждены для катушек с внешним диаметром (dout) от 100 до 480 мкм, внутренним диаметром (din) от 0,1 до 0,9 dout, шириной провода (w) от 2 мкм до 0,3 dout, зазором между витками ( s) от 2 мкм до 3 dout и значение индуктивности от 0,5 до 100 нГн. Выражение Data Fitted Monomial было разработано с использованием авторской базы данных индукторов с использованием методов подбора данных.По этой причине, когда характеристики анализируемой катушки отличаются от характеристик в базе данных, ошибка между формулой и индуктивностью катушки может быть значительной. Геометрия катушки, которую можно использовать, и соответствующие коэффициенты представлены в таблице 1. Формула индуктивности основывается на этом наборе геометрических зависимых коэффициентов и в параметрах катушки для расчета собственной индуктивности:L = βdoutα1wα2davgα3Nα4sα5
(1)
где: dout соответствует внешнему диаметру, w – ширине витка, davg – среднему диаметру (davg = dout + din2), din – внутреннему диаметру, N – количеству витков, а s – пространству между витками. (видно на рисунке 1).Формула приближения токового слоя основана на приближении сторон катушки к токовым слоям равной плотности с использованием электромагнитных принципов. В этой формуле расчет автоматической и взаимной индуктивности между проводами катушки выполняется с учетом концепции среднего геометрического расстояния (GMD), среднего арифметического расстояния (AMD) и среднего арифметического расстояния (AMSD) [35]. Благодаря такому подходу, чем больше соотношение между расстоянием между витками и шириной дорожки, тем больше погрешность между этой формулой и реальной индуктивностью катушки.В таблице 2 показаны схемы катушек, для которых применим этот подход, и соответствующие коэффициенты, которые необходимо применить:L = μ0N2davgc12 (ln (c2ρ) + c3ρ + c4ρ)
(2)
где μ0 – проницаемость вакуума, равная 4π × 10−7N / A2, davg – средний диаметр, N – количество витков, ρ – коэффициент заполнения (ρ = dout − dindout + din). Модифицированная формула аппроксимации Уиллера. выводится из формул Уиллера. В [36] Уиллер представил несколько формул для расчета индуктивности спиральных катушек с одним или несколькими слоями, а Mohan et al.предложил приближение, позволяющее сделать формулы Уиллера справедливыми для плоских катушек [35]. Таким образом, они вывели уравнение, которое зависит от двух коэффициентов (k1 и k2), связанных с компоновкой катушки, вакуумной проницаемости и некоторых геометрических параметров катушки, таких как количество витков (N), ее средний диаметр (davg ) и коэффициент заполнения (ρ). В таблице 3 показаны допустимые схемы расположения катушек и значения соответствующих коэффициентов для применения в:Поскольку эта аппроксимирующая формула зависит только от среднего диаметра и степени заполнения змеевика, она не имеет значения для различных конфигураций s и w, когда значения davg и ρ одинаковы.В этих случаях ошибка, связанная с этой моделью, увеличивается.
Популярность этих трех формул аппроксимации весьма различна. Из исследований, найденных в литературе, можно утверждать, что формула аппроксимации текущего листа является наиболее используемой [8,19,20,21,22,23,24,37,38], за которой следует модифицированная формула Уиллера [8,19,20,21,22,23,24,37,38]. 24,30] и Data Fitted Monomial [26,39]. Что касается расчета индуктивности многослойной планарной катушки, это зависит от параметризации катушки на каждом слое (геометрия, количество витков, расстояние между витками , ширина проволоки, внутренний и внешний диаметр) и расстояние между ними.Таким образом, чтобы получить полную индуктивность двухслойной катушки, необходимо суммировать самоиндуктивности каждого слоя и суммировать или вычитать, в зависимости от направления тока, удвоенную взаимную индуктивность между слоями [ 20,21,33]: где LT – полная индуктивность, L1 и L2 – значения самоиндукции катушек в каждом слое, а M – взаимная индуктивность между двумя катушками, которую можно рассчитать с помощью: где K – коэффициент связи между витками каждого слоя.В настоящее время для выполнения этих расчетов используется комбинация коэффициента связи со значениями самоиндукции, полученными по ранее упомянутым аппроксимационным формулам [37,40]. Обычно этот коэффициент рассчитывается либо аналитически [24], либо с использованием численной модели [25], либо даже может быть измерен экспериментально [41]. Уравнение (6) – это аналитическое выражение, которое обычно используется для расчета коэффициента связи между катушками [20,21,24]. Он был получен Чжао экспериментально с помощью многослойных катушек с расстоянием между соседними слоями, изменяющимся от 0.От 75 мм до 2 мм, учитывая катушки с 5-20 витками [20,21,24]. Это уравнение имеет особенность того, что оно действительно только в пределах полученного диапазона, а катушки всех слоев должны быть одинаковыми и идеально выровненными.M = 2KcL1L2Kc = N20,64 [(0,184X3−0,525X2 + 1,038X + 1,001) (1,67N2−5,84N + 65)]
(6)
где Kc – коэффициент связи, N – количество витков катушки, а X – расстояние между слоями в мм [20,21,24].Короче говоря, можно сделать вывод, что определение конструкции однослойной плоской катушки с использованием одной из трех формул аппроксимации является простым и быстрым процессом, не требующим больших вычислительных ресурсов.Однако, как указывалось ранее, эти формулы действительны только для определенной геометрии катушки и не имеют такой же точности, как моделирование методом конечных элементов. Можно даже сказать, что на его точность влияет геометрическая конфигурация анализируемой катушки, например, в случае выражения Data Fitted Monomial, его ошибки будут больше для ситуаций, в которых катушки находятся за пределами диапазона вывода уравнения. . В случае аппроксимации токового листа, чем больше расстояние между витками по отношению к ширине провода, тем больше ошибки; и в случае модифицированных катушек Уиллера с различными комбинациями промежутков между витками и шириной дорожки, но с суммой двух постоянных, это приведет к тому же результату индуктивности.При рассмотрении двухслойных плоских катушек одно из трех упомянутых выше уравнений может использоваться вместе со вспомогательным уравнением для определения коэффициента связи между слоями. Простота, скорость и низкая стоимость аналитического процесса расчета индуктивности для однослойных планарных катушек в большинстве случаев могут быть достигнуты с помощью этих моделей, которые можно найти в литературе. Однако ограничение самого уравнения коэффициента связи, которое справедливо только для катушек с 5-20 витками и с соседними слоями, расположенными между 0.75 мм и 2 мм, не позволяет считать эти решения жизнеспособными для всех конфигураций расчета многослойного планарного змеевика.
Принимая во внимание ограничения представленных аналитических методов, ограничения моделирования FEM и растущий интерес к продуктам с многослойными планарными катушками, становится желательным для нескольких отраслей промышленности иметь универсальный, быстрый, открытый исходный код и точный инструмент для ускорения процесса проектирования. В этой статье предлагается приближенная модель, сочетающая универсальность компоновки катушек со скоростью, точностью, простотой управления и взаимодействия.В следующем разделе описывается предлагаемый инструмент, который, в отличие от других методов, соответствует потребностям отраслей.
4. Результаты и обсуждения
Предложенная модель была подтверждена путем сравнения результатов с известными аналитическими формулами, упомянутыми в разделе 2 (для геометрий, к которым они применимы), с учетом одно- и многослойных плоских катушек [20], а также с помощью моделирования методом конечных элементов и экспериментальных измерений, выполненных на печатных катушках печатной платы. Помимо различного количества слоев, во время валидации были протестированы другие параметры катушки, такие как ширина линии (w), расстояние между витками (s), количество витков (N) и количество сегментов на виток (Ns).Поскольку типичные аналитические формулы действительны только для катушек с 4, 6 и 8 сегментами на виток, катушки с 10 и 12 сегментами в каждом витке были проверены только с использованием результатов МКЭ и экспериментальных измерений. Что касается w и s, с учетом ограничений формулы аппроксимации текущего листа, одинаковые значения были приняты во внимание для обоих параметров (s = w), а именно 0,15 мм и 0,10 мм. Также было учтено, что согласно [20] выражение для коэффициента связи, необходимое для многослойных расчетов, справедливо только для катушек с 5–20 витками с расстоянием между слоями от 0.От 75 мм до 2,0 мм. Все настройки, использованные в различных случаях моделирования, сведены в Таблицу 4.4.1. Аналитические модели в сравнении с моделью МКЭ
В этом разделе было проведено сравнение значений индуктивности катушки, полученных с помощью предложенной модели, с аналитическими формулами и с результатами моделирования МКЭ, использованными в качестве эталонных значений.
На рисунках 5A – E и 6 показаны примеры геометрии катушек с 1 и 2 слоями соответственно, использованных в этом анализе. Как упоминалось ранее, из-за ограничений применимости традиционных аналитических формул они применялись только к схемам A – C на рисунках 5 и 6.Моделирование методом МКЭ выполнялось в программном обеспечении ANSYS Electronic Software как магнитная задача, в частности, в режиме вихревых токов. Она также изучалась как проблема магнитостатики, но не рассматривалась как актуальная для данного исследования, учитывая необходимость проведения экспериментальной проверки. Модель FEM рассматривает воздушную коробку с размером стороны, в пять раз превышающим внешний диаметр змеевика. Предыдущие исследования гарантируют, что большие размеры воздушной камеры не изменят результаты моделирования более чем на 1%, как показано на рисунке 7A для примера однослойной квадратной катушки и на рисунке 8 для примера двухслойной квадратной катушки.В обеих моделях использовался испытательный ток 1 мА, при этом частота решателя была выбрана равной 1 МГц, чтобы соответствовать экспериментальной испытательной частоте. Адаптивная установка была сконфигурирована с процентной ошибкой 1% и минимум двумя шагами сходимости. Что касается параметров сетки, тип, выбранный для анализируемых случаев моделирования, основывался на аппроксимации поверхности как для змеевика, так и для воздушной камеры. . Вокруг катушки и самой катушки была назначена более мелкая сетка (например, рисунок 9B), так как это была критическая область для расчета самоиндукции, в то время как для воздушной камеры использовалась более грубая сетка (например.g., Рис. 9A). На Рис. 10 и Рис. 11 показаны результаты самоиндукции для различных схем однослойной катушки (см. Рис. 5A – E), рассчитанные с использованием различных моделей. На рисунке 10 представлены значения индуктивности для катушек с 4 и 10 витками, с внутренним сегментом 0,3 мм и зазором между витками и шириной провода 0,15 мм. Если рассматривать результаты МКЭ в качестве эталона, набор результатов, показанный на рисунке 10, показывает, что диапазон ошибок в результатах по модифицированному методу Уиллера варьировался от 0.99% до 12,67% и от 2,93% до 9,39% с использованием метода аппроксимации текущего листа. Ошибка, зарегистрированная с помощью монома с подгонкой данных, составляла от 2,08% до 9,31% и от 2,13% до 7,93% с использованием предложенной модели. В остальных проанализированных вариациях катушек (катушки с 10 и 12 сегментами на виток) предложенная модель показывает ошибки от 1,39% до 2,45%. На рисунке 11 показаны данные для катушек с 4 и 10 витками, с внутренним сегментом 1,3 мм и с двумя комбинациями расстояния между витками и шириной провода w, w = s = 0.10 мм и w = s = 0,15 мм. Посредством запроса графиков можно проверить, что модифицированный метод Уиллера для N4 имел диапазон ошибок [0,35–15,04%], а для N10 – [0,18–35,85%]. Применяя аналогичный анализ, метод аппроксимации текущего листа имел диапазон ошибок [1,45–6,74%] для N4 и [0,04–6,31%] для N10, в то время как мономиальный анализ данных показал [0,69–11,31%] для N4 и [0,55 –3,51%] для N10. Что касается модели, предложенной в этой работе, для четырехвитковых катушек полученные ошибки были между 0.06% и 5,90%, а для 10 оборотов от 0,78% до 2,47%. В частности, при рассмотрении геометрии катушки с 10 и 12 сегментами диапазон ошибок упал до значений от 0,59% до 3,99% для N4 и от 0,62% до 0,79% для N10. Учитывая это, можно увидеть, что ошибки предложенной модели были на том же уровне, что и диапазон ошибок из общих формул, со значительным преимуществом отсутствия каких-либо ограничений, связанных с геометрией, и представления более низких диапазонов ошибок, чем некоторые из приближенные выражения.Та же процедура проверки была использована для двухслойных планарных катушек. Учитывая это, и чтобы иметь возможность рассчитать самоиндукцию многослойных катушек с использованием общих выражений, необходимо было выполнить дополнительный расчет (для коэффициента связи между различными слоями) [20,21]. На основании этого и анализа результатов, представленных на рисунках 12 и 13, можно заметить, что предложенная модель позволила получить более точные вычисления по сравнению с общими выражениями.С учетом результатов, полученных для двухслойных катушек на 10 витков, рисунок 13, общее выражение показало лучшую производительность, чем для двухслойных катушек с четырьмя витками, рисунок 12, с ошибками до 4,42% для квадратной геометрии, 10,83% для гексагональной и 6,57% для восьмиугольной, если расстояние между катушками было ограничено диапазоном от 0,75 мм до 2 мм (ограничение расчета коэффициента связи для общих выражений). Для тех же выбранных случаев предложенная модель показала максимальные ошибки 3.53% для квадратных катушек, 2,22% для гексагональных катушек, 1,56% для восьмиугольных катушек и 1,23% для декагональных катушек.Можно сделать вывод, что даже в пределах диапазона, в котором может применяться расчет коэффициента связи общих выражений, результаты, полученные с использованием предложенной модели, были более точными, с небольшими отличиями от результатов моделирования методом конечных элементов. Кроме того, если принять во внимание строгие геометрические ограничения общих выражений и расчета коэффициента связи, можно легко утверждать, что разработанная модель была способна объединить надежные результаты с универсальным методом расчета.
4.2. Экспериментальная проверка
Для полной проверки предложенной модели были выполнены экспериментальные измерения самоиндукции для нескольких геометрий изготовленных катушек. Для этого эксперимента минимальная ширина линии (w) и интервал (s), используемые в испытательных катушках, составляли 0,15 мм из-за ограничений производителя печатной платы. На рисунке 14A показана печатная плата, изготовленная с использованием различных однослойных катушек, а именно 4, 6, 8 и 10 сегментов на виток, с внутренним сегментом 1,3 мм. Эти катушки были сгруппированы в два набора: один с десятью витками (в верхней строке) и другой с восемью витками (в нижней строке).В каждой линии и для каждой геометрии была пара катушек, одна с w = s = 0,15 мм, а другая с w = 0,15 мм и s = 0,20 мм. На Рисунке 14B были видны двухслойные катушки, показывающие различную геометрию из 4, 6, 8 и 10 сегментов на виток с внутренним сегментом 1,3 мм. Для двухслойной катушки были изготовлены только катушки с 10 витками. Расстояние между каждой катушкой было выбрано таким образом, чтобы пространство было максимальным, без создания какого-либо эффекта при экспериментальном измерении одиночной катушки.Это было подтверждено сравнением результатов для платы с одной катушкой и измерительной установкой с несколькими катушками, без выявления серьезных различий. Чтобы свести к минимуму любую ошибку в измерительной установке, а также в процессе изготовления катушек, были изготовлены два набора печатных плат, и самоиндуктивности в обоих из них были измерены тринадцать раз. Прецизионный измеритель LCR компании Keysight Technologies E4980AL-102 использовался для измерений индуктивности на испытательной частоте 1 МГц с настраиваемой настройкой четырехточечного датчика Кельвина.Чтобы свести к минимуму ошибки измерения, измерительная установка, изображенная на рисунке 14B, была разработана для подключения печатной платы катушек к измерителю LCR после процесса калибровки (рисунок 15). Для сравнения экспериментального измерения изготовленных катушек с используемой моделью FEM Для сравнения, тринадцать измерений LCR были усреднены. В процессе экспериментальной оценки максимальное отклонение, зарегистрированное на обеих печатных платах, составило около 0,68% для однослойных катушек и 0,48% для двухслойных катушек, что свидетельствует о высокой точности измерений.Экспериментальное моделирование методом конечных элементов с помощью соединителя и результаты предлагаемой модели для конструкции однослойной катушки показаны на рисунке 16. Подробный анализ относительных ошибок между экспериментальными измерениями показан на рисунках 17 и 18. Примечательно, что для проведения измерений на печатные катушки были добавлены две дорожки, от концов катушки до разъемов. По этой причине ожидалось, что значения индуктивности, измеренные с помощью LCR, должны быть выше, чем значения, полученные из модели и моделирования FEM, представленных ранее (поскольку он учитывал только элемент катушки).Чтобы понять влияние и количественно оценить этот эффект, была создана модель МКЭ с двумя соединительными дорожками, выходящими из змеевика в сторону воздушной камеры.Как и предполагалось, при рассмотрении соединительных дорожек была зарегистрирована более высокая индуктивность и ошибка экспериментального измерения была минимизирована. Сравнивая данные для однослойных катушек из модели FEM, можно заметить, что учет соединительных проводов привел к снижению погрешности примерно на 2% для N = 10 и на 3% для N = 8.
Наконец, результаты, рассчитанные с помощью предложенной модели, были сопоставлены с экспериментальными измерениями, как показано на рисунках 17 и 18.Погрешности моделей FEM, с разъемами и без них, также были добавлены к представлению, всегда используя экспериментальное измерение в качестве эталона. Обратите внимание, что схемы катушек, смоделированные с помощью предлагаемой модели, не включали расширенных соединительных трасс (см. Рисунок 5 и Рисунок 6).Сравнивая ошибки модели FEM без соединителей и ошибки предложенной модели, можно заметить, что основной вклад в эти ошибки вносило отсутствие соединительных трасс в анализе.Даже при такой разнице в геометрии погрешности между экспериментальными измерениями и ошибками предложенной модели остаются в приемлемом диапазоне: в случае однослойных катушек менее 9% для квадратных катушек, 6% для гексагональных катушек, 5 % для восьмиугольных катушек и 4% для десятиугольных катушек. В случае двухслойных катушек он был дополнительно минимизирован до значений менее 5% для квадратных катушек, 3% для гексагональных катушек, 2,5% для восьмиугольных катушек и 2% для десятиугольных катушек. Таким образом, можно сделать вывод, что предложенная модель верна и имеет хорошую точность для расчета индукции как одно-, так и двухслойных катушек.


