Фильтры RC. Частота среза. Расчёт онлайн.
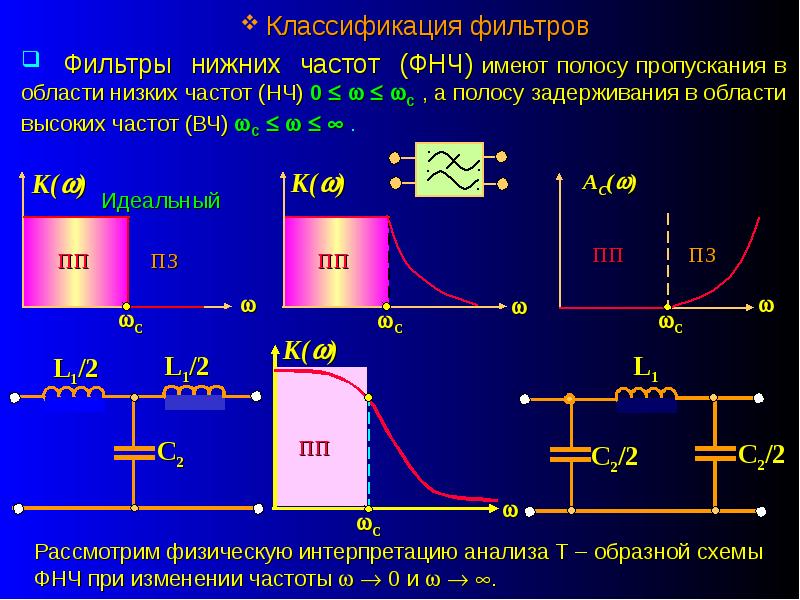
Фильтр нижних частот (ФНЧ) – электрическая цепь, эффективно пропускающая частотный спектр сигнала ниже определённой частоты, называемой частотой среза, и подавляющая сигнал выше этой частоты.
Фильтр высших частот (ФВЧ) – электрическая цепь, эффективно пропускающая частотный спектр сигнала выше частоты среза, и подавляющая сигнал ниже этой частоты.
Рассмотрим в качестве фильтра простейшую цепь RC, принцип работы которой основан на зависимости реактивного сопротивления конденсатора от частоты сигнала.
Если к источнику переменного синусоидального напряжения U частотой f подключить последовательно резистор сопротивлением R и конденсатор ёмкостью C, падение напряжения на каждом из элементов можно вычислить исходя из коэффициента деления с импедансом Z.
Импеданс – комплексное (полное) сопротивление цепи для гармонического сигнала.
Z² = R² + X² ; Z = √(R² + X²) , где Х – реактивное сопротивление.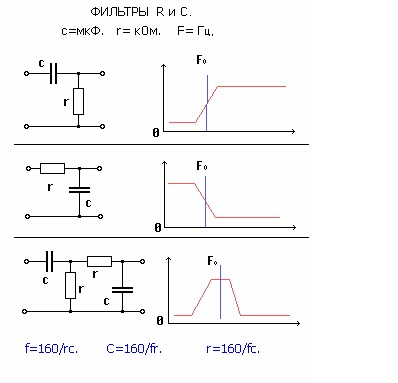
Тогда на выводах резистора напряжение UR будет составлять:
XC – реактивное сопротивление конденсатора, равное 1/2πfC
При равенстве R = XC на частоте f, выражение упростится сокращением R и примет вид:
Следовательно, на частоте f равенство активного и реактивного сопротивлений цепочки RC обеспечит
одинаковую амплитуду переменного синусоидального напряжения на каждом из элементов в √2 раз меньше входного напряжения,
что составляет приблизительно 0.7 от его значения.
В этом случае частота f определится исходя из сопротивления R и ёмкости С выражением:
τ – постоянная времени цепи RC равна произведению RC
Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт.
Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе.
Зависимость амплитуды переменного напряжения от его частоты называют амплитудно-частотной характеристикой (АЧХ).
Если рассмотреть АЧХ напряжения на выводах конденсатора или резистора в RC цепи, можно наблюдать на частоте f = 1/(2π τ) спад уровня до значения 0.7, что соответствует -3db по логарифмической шкале.
Следовательно, цепь RC может быть использована как фильтр нижних частот (ФНЧ) – красная линия на рисунке, или фильтр высших частот (ФВЧ) – синяя линия.
Ниже представлены схемы включения RC-цепочек в качестве фильтров соответственно ФНЧ и ФВЧ.
Частоту f = 1/(2π τ) называют граничной частотой
Частоту среза фильтра можно посчитать с помощью онлайн калькулятора
Достаточно вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Пост. времени τ RC и частота среза RC-фильтра |
Похожие страницы с расчётами:
Расчёт импеданса.
Расчёт резонансной частоты колебательного контура.
Расчёт компенсации реактивной мощности.
Замечания и предложения принимаются и приветствуются!
Мои закладки. Фильтр LC. Расчет. Калькулятор. Катушка.
Мои закладки. Фильтр LC. Расчет. Калькулятор. Катушка.Мои закладки. Фильтр LC. Расчет. Калькулятор. Катушка.
Расчет LC. Резонанс колебательного контура. Фильтр.
Расчет частоты резонанса колебательного контура … Калькулятор расчета резонанса в контуре … Расчет частоты резонанса колебательного контура. Колебательный контур LC. Свободные электрические колебания в параллельном контуре. Расчёт частоты резонанса LC-контура, простой онлайн-калькулятор …
Coil32 – On-line калькуляторы витков катушки, расчет однослойной индуктивности . .. Калькулятор расчета однослойной катушки индуктивности … Расчет Катушка Индуктивность Витки : On-line калькуляторы. Расчет однослойной катушки …
.. Калькулятор расчета однослойной катушки индуктивности … Расчет Катушка Индуктивность Витки : On-line калькуляторы. Расчет однослойной катушки …
Свойства катушек индуктивности … Электричество и магнетизм. Общая электротехника и электроника. Расчет Индуктивность Свойства. Свойства катушек индуктивности. Электричество и магнетизм. Общая электротехника и электроника. Накопленная энергия в индуктивности. Гидравлическая модель. Индуктивность в электрических цепях. Схемы соединения катушек индуктивностей. Параллельное соединение индуктивностей. Последовательное соединение индуктивностей. Добротность катушки индуктивности. Катушка индуктивности. Формула индуктивности. Базовая формула индуктивности катушки. Индуктивность прямого проводника. Индуктивность катушки с воздушным сердечником. Индуктивность многослойной катушки с воздушным сердечником. Индуктивность плоской катушки. Конструкция катушки индуктивности. Применение катушек индуктивности. Расчет катушек индуктивности. Метод определения собственной емкости катушек.
Емкость. Свойства. Расчет. Электростатика … Электричество и магнетизм. Общая электротехника и электроника. Электростатические машины и лейденская банка. Диэлектрики. Диэлектрическая проницаемость. Проводники. Коммутационные устройства. Удельное сопротивление. Резисторы. Разность потенциалов. Электрическая емкость, конденсаторы. Индуктивные элементы. Свойства катушек индуктивности. Постоянный ток. Источники постоянного тока и напряжения (ЭДС). О реальных явлениях электромагнетизма …
Индуктивные элементы … Электричество и магнетизм. Общая электротехника и электроника. Индуктивные элементы … Расчет Идуктивность Свойства. Индуктивные элементы. Катушки индуктивности и трансформаторы. Катушки контуров. Катушки связи. Дроссели высокой частоты. Дроссели низкой частоты …
Онлайн расчёт RC фильтров … RC-фильтры … Расчет Фильтр ФНЧ ФВЧ. Онлайн расчёт RC фильтров. Схема и частотная характеристика. Частота среза фильтра. RC-фильтры предстваляют собой цепочку, состоящую из резистора и конденсатора. В зависимости от их расположения фильтр пропускает или верхние или нижние частоты …
RC-фильтры предстваляют собой цепочку, состоящую из резистора и конденсатора. В зависимости от их расположения фильтр пропускает или верхние или нижние частоты …
Расчёт LC – фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ … Онлайн калькулятор LC фильтров … Расчет LC – фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ. Калькуляторы ФНЧ, ФВЧ, резонансных, полосовых LC фильтров. Индуктивность катушки. Активное сопротивление катушки. Емкость конденсатора. Резонансная частота фильтра. Добротность фильтра Q. Характеристическое сопротивление. Полоса пропускания фильтра …
Многозвенные LC фильтры … Онлайн калькулятор многозвенных полосовых LC фильтров … Расчет ФНЧ ФВЧ 3 5 7 порядка – Т и П типа. Онлайн расчёт многозвенных LC – фильтров. Калькулятор ПФ, ФВЧ, ФНЧ 3-го, 5-го и 7-го порядков. Фильтр Чебышева. Фильтр Баттерворта. Одиночный LC фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области обычно используют многозвенные LC фильтры . ..
..
Режекторные эллиптические фильтры образуют конденсаторы, установленные катушкам – параллельно в ФНЧ или последовательно в ФВЧ … Онлайн калькулятор многозвенных элиптических LC фильтров … Расчет фильтр эллиптический Кауэра. Онлайн расчёт многозвенных эллиптических LC – фильтров Кауэра ПФ, ФВЧ, ФНЧ 3-го, 5-го и 7-го порядков. Крутизна спада амплитудной характеристики линейных фильтров показала себя недостаточно. В отличии от классических линейных аналогов наличие дополнительных конденсаторов, включенных параллельно в ФНЧ (или последовательно в ФВЧ) катушкам индуктивности – образуют режекторные фильтры и формируют дополнительную крутизну спада АЧХ эллиптических фильтров …
Онлайн калькулятор полосовых LC фильтров … Онлайн калькулятор, расчет полосовых LC фильтров 3 / 5 / 7 порядка … Калькулятор полосовых LC фильтров Чебышева … Полосовой, он же полосно-пропускающий фильтр – это фильтр, пропускающий частоты в некоторой полосе, находящейся между нижней и верхней частотами среза .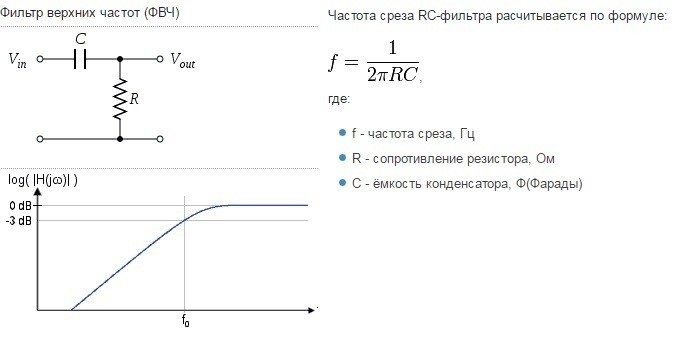 .. Он может быть легко представлен в виде последовательности, состоящей из ФНЧ / фильтра нижних и ФВЧ / фильтра верхних частот …
.. Он может быть легко представлен в виде последовательности, состоящей из ФНЧ / фильтра нижних и ФВЧ / фильтра верхних частот …
Калькулятор.
Калькулятор геодезических куполов, 3D дизайн со вращением мышью, расчет размеры … Расчет купольного дома из треугольников … Интересный купольный сферический дом предлагают самостоятельно изготовить из обычных треугольников … Для его расчета можно воспользоваться онлайн калькулятором … Чем больше треугольников – тем, получится, более округлая сфера …
Планета калькуляторов, онлайн калькуляторы … Онлайн калькулятор – Сегмент круга … Вычисление сегмента по хорде и высоте … Площадь сегмента круга по радиусу и высоте … Круговой сегмент – все варианты расчета …
Формулы – геометрия, алгебра, физика … Формулы круга … Все основные формулы для определения длины радиуса окружности. Окружность и круг. Радиус окружности. Длина хорды окружности. Высота сегмента круга. Площадь круга. Длина окружности.
Сервис бесплатных строительных калькуляторов … Адаптация расчетов под мобильные телефоны и Android … Строительные калькуляторы … Общестроительные работы, калькулятор нагрузки, металл, железобетон, дерево, инженерные коммуникации, отделка, расчет размеров, теплотехника, электрика. Перевод единиц измерения …
Некоторые полезные онлайн калькуляторы … Интерактивные утилиты преобразования … Калькулятор / конвертер … Конвертер цифровой базы. Конвертер текущая дата / время GMT. Координаты, современный вариант Lat / Lon в NMEA 0183 dddd.mmmm, HASH строки, Конвертер HEX / DEC / Строка …
Закон Ома. Онлайн калькулятор. Учеба и наука, Физика … Онлайн калькулятор – закон Ома … Закона Ома определяет связь между током, напряжением и сопротивлением в электрических цепях …
Конвертер.
Base64 Decode и Encode – Online … Base64 – декодирование и кодирование … Калькулятор / конвертер Base64 Decode / Encode .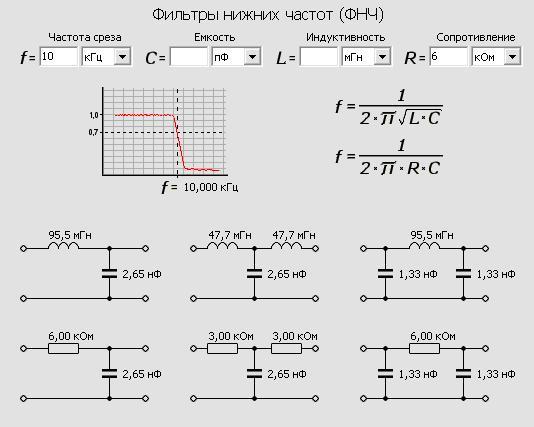
Алфавит Base32 и Base64 … Гари Кесслер Ассошиэйтс … Обучение, образование и консалтинговые услуги … Алфавит Base32 (5-бит), Base64 (6-бит) из RFC4648 …
Integer Base конвертер для программистов на C# … Системы счисления на базе 2 10 16, перевод … Если вы программист, вы знаете разные системы счислений. В повседневной жизни нас обычно устраивает система счисления на базе 10. Но компьютерный мир совсем другой. Бинарный характер хранения данных на компьютере двоичная система на базе 2 и числа длинной двоичной строки – читать нелегко. Шестнадцатеричная система на базе 16 делает строки короче – но также непонятно для знакомых нам человеческих десятичных обозначений. Для работы с цифрами, написанными в разных системах позиционных цифр, нужны инструменты для перевода чисел с одной базы на другую …
Конвертер регистров текста – конвертировать онлайн верхний регистр в нижний, нижний регистр в верхний и другие варианты … Текстовые утилиты онлайн … Конвертер регистров текста .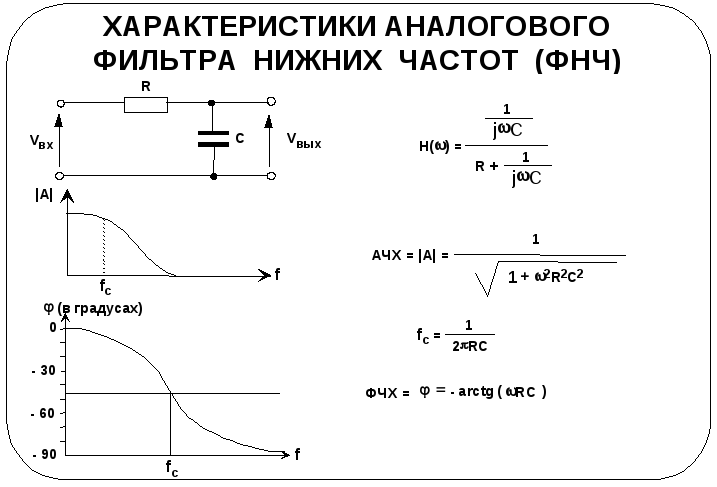 .. Конвертировать онлайн верхний регистр в нижний … Нижний регистр в верхний и другие варианты …
.. Конвертировать онлайн верхний регистр в нижний … Нижний регистр в верхний и другие варианты …
Популярное : …
… Найти … Как улучшить фото … Делфи на Андроид … Погода М-4, М-5, М-7, Р-22 … Список торрент трекеров … Калькулятор кода радио … Частота в длину волны … RTL SDR Radio …
TechStop-Ekb.ru : познавательные развлечения, техника, технологии … На сайте, для работы и соответствия спецификациям – используются … Протокол HTTPS шифрования для безопасного соединения с сервером и защиты пользовательских данных … Антивирус DrWeb для превентивной защиты пользователей от интернет угроз и вирусов … Ресурс входит в рейтинги Рамблер Топ 100 (познавательно-развлекательные сайты) и Mail Top 100 (авто мото информация) …
Тех Стоп Екб RU (РФ) официальный сайт, популярные темы, погода, новости, обзоры с картинками, бесплатно, актуально, без регистрации … Смотреть утром, днем, вечером и ночью – круглосуточно онлайн . ..
..
Меню раздела, новости и новые страницы.
… | … ТехСтоп Екб … | … Главное меню … | … Быстрый поиск … | …
© 2021 Тех Остановка Екатеринбург, создаваемый с 2016++ с вами вместе навсегда бесплатно …
RC-цепи, 5 самых распространенных и как просто их рассчитать
RC-цепь, такое частое явление радиоэлектроники. Такие фильтры стоят повсюду. Понимание того, как какой фильтр влияет на форму АЧХ сигнала во многом определяет правильность чтения всей электронной схемы. В статье собраны 5 основных RC-фильтров, приведены их АЧХ и упрощенные формулы расчета.
Содержание:
- Введение
- 1. Фильтр Низких Частот
- 2. Фильтр Высоких Частот
- 3. Избирательный фильтр
- 4. Т-образные фильтры
- 5. Двойной Т-образный фильтр
В ранние годы развития радиоэлектроники для воздействие на Амплитудно — Частотную Характеристику (АЧХ) сигнала в основном применялись LC — фильтры, т. е. фильтры состоящие из катушки индуктивности и конденсатора. Со временем им на смену пришла RC-цепь, которая была плотно взята в оборот радиоэлектроникой ввиду меньшей стоимости и габаритов.
е. фильтры состоящие из катушки индуктивности и конденсатора. Со временем им на смену пришла RC-цепь, которая была плотно взята в оборот радиоэлектроникой ввиду меньшей стоимости и габаритов.
Конечно, фильтры на RC-цепях не могут полностью вытеснить LC собратьев. Например в фильтрах для АС предпочтительнее использование LC-фильтров. Но практически во всей маломощной электронике главенствуют именно RC-цепи. Например двойная RC-цепь в фильтре RIAA-корректора.
Упрощенные формулыИнтересным вариантом избавления от катушек являются фильтры на гираторах, где посредством конденсатора и операционного усилителя эмитируется работа катушки.
Для простого расчета фильтров далее приведены упрощенные формулы, позаимствованные из инженерного справочника.
В формулах присутствует коэффициент 160000 (сто шестьдесят тысяч). Эта цифра возникает по двум причинам.
- Во-первых предполагается брать величину емкости при расчетах в микрофарадах (10-6 Фарада)
- Во-вторых при переходе от круговой частоты к цикличной возникает множитель 2π
Соответственно:
1 / (2⋅π⋅10-6) = 159154 ≈ 160000
Итак, давай те же перейдем к самим фильтрам.
1. Фильтр Низких Частот (ФНЧ) — он же интегратор:ФНЧ — фильтр, пропускающий без изменения частоты ниже частоты среза (f0) и подавляющий частоты выше f0. На частоте среза имеет значение амплитуды в -3dB. Это фильтр первого порядка и крутизна среза составляет 6дБ/октаву. Чаще всего такие фильтры используются для отсечения высокочастотных помех и шумов.
2. Фильтр Высоких Частот (ФВЧ) — он же дифференциаторОктавой называется такой интервал частот, у которого конечное значение частоты больше начального в два раза.
ФВЧ — фильтр, ослабляющий частоты ниже частоты среза(f0) и пропускающий без изменения частоты выше f0. Так же как и у приведенного выше ФНЧ, сигнал на частоте среза обладает амплитудой в -3дБ, а крутизна среза 6 дБ на октаву.
И ФНЧ и ФВЧ работают как делитель напряжения, в котором одно плечо представлено постоянным резистором, а второе конденсатором, имеющим частотную зависимость.
Такие фильтры часто применяются на выходах звуковых усилителей для отсечения инфранизких, которые могут повредить АС.
3. Избирательный фильтрТакой фильтр выделяет определенную частоту или полосу частот за счет подавления других частот. По сути этот фильтр представляет из себя последовательное включение ФНЧ и ФВЧ.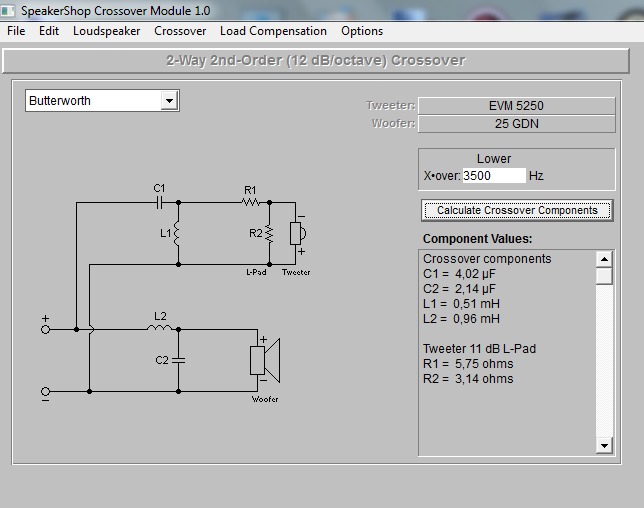 Соответственно при равенстве между собой емкостей и сопротивлений выделена будет определенная частота, а в обе стороны будет ослабление с крутизной 6 дБ/окт .
Соответственно при равенстве между собой емкостей и сопротивлений выделена будет определенная частота, а в обе стороны будет ослабление с крутизной 6 дБ/окт .
Но никто не мешает расширить полосу пропускания, если рассчитать каждую RC-цепь R1С1 и R2C2 для разных f0.
4. Т- образные фильтрыТ- образные фильтры это те же Г-образные фильтры низкой частоты и высокой частоты, к которым добавляется еще один элемент. Но особенностью Т-образных фильтров является то, что по сравнению с Г-образными, они оказывают меньшее шунтирующее действие на цепи стоящие за фильтром.
5. Двойной Т-образный фильтр — пробкаФильтр имеет бесконечное затухание (порядка 60дБ) которое возникает благодаря сложению двух сигналов имеющих на частоте среза разность фаз 180. Применение такого фильтра весьма эффективно для устранения сигнала помехи. Например сетевой наводки 50Гц.
Например сетевой наводки 50Гц.
Если Вам интересна тема фильтров, то возможно, Вас так же заинтересует: Фазово-частотная характеристика (ФЧХ) фильтров и звук
3. Понятие оптимальной фильтрации – Физический факультет СПбГУ
Оптимальное выделение сигнала из шума можно проводить различными методами, в зависимости от того, какая ставится задача — обнаружение сигнала, сохранение формы сигнала и т.д. В каждом методе оптимальной фильтрации вводится понятие критерия оптимальности, согласно которому строится оптимальный алгоритм обработки сигнала [ 11].
Конкретный алгоритм оптимальной фильтрации будет существенно зависеть от того непериодический или периодический сигнал должен быть выделен (обнаружен) на фоне шума. По отношению к периодическому сигналу далее различаются ситуации: известна или нет его частота повторения. Ниже эти варианты задач будут рассмотрены последовательно.
3.1 Оптимальная фильтрация непериодического (одиночного) сигнала
Оценим возможную эффективность обнаружения непериодического сигнала при его аддитивной смеси с белым шумом. При формулировке задачи нахождения коэффициента передачи «оптимального» фильтра используются существенные требования относительно сигнала: во-первыхсчитается известной форма сигнала f(t) и соответственно его спектр , во вторых сигнал считается ограниченным во времени:
(3.1)
Т.е. сигнал имеет конечную длительность.
Определение оптимальности фильтра формулируется следующим образом:
Оптимальным фильтром в задаче обнаружения одиночного импульса конечной длительности является фильтр, обеспечивающий максимальное отношение пиковой мощности сигнала к мощности шума в момент окончания импульса.
Комплексный коэффициент передачи такого оптимального фильтра прямо определяется спектром заданного, подлежащего обнаружению сигнала (т. е. его формой и длительностью ) [2 ]
е. его формой и длительностью ) [2 ]
Так, если сигнал имеет спектр
(3.2)и длительность его , то функция
есть функция комплексно сопряженная функции спектральной плотности сигнала.
Можно показать [2], что комплексный коэффициент передачи оптимального фильтра, в приведенном выше смысле определяется так:
или
(3.3)
Не воспроизводя выкладки доказательства формулы (3.3) приведенных в ряде источников (например [ 2] ), остановимся на физическом смысле результата.
Замечая, что фазовая характеристика коэффициента передачи в (3.3) есть
видим, что — компенсирует фазовые сдвиги составляющих сдвиги спектра сигнала (3.2), что формирует «пик» импульса на выходе, а линейная функция — обеспечивает задержку этого «пика» на время длительности сигнала, т. е. этот пик приходится на момент окончания сигнала.. Можно сказать, что обеспечивается накопление полезного сигнала на интервале всего времени существования импульса.
е. этот пик приходится на момент окончания сигнала.. Можно сказать, что обеспечивается накопление полезного сигнала на интервале всего времени существования импульса.
Формула (3.3) устанавливает также, что модуль коэффициента передачи должен совпадать с модулем спектральной плотности функции заданного сигнала, т. е. оптимальный фильтр ослабляет спектральные составляющие шума тем сильнее, чем меньше модуль , В результате полная мощность шума на выходе фильтра оказывается меньшей, чем при равномерной АЧХ.
Наконец отметим, что произвольная константа размерна. При безразмерном имеет размерность обратной спектральной плотности сигнала.
3.2. Оценка отношения сигнал/шум при оптимальном фильтре
Будем исходить из приведенного выше выражения (3.3). Заметим, что для сигнала (импульса) сложной формы синтез оптимального фильтра является не простой задачей.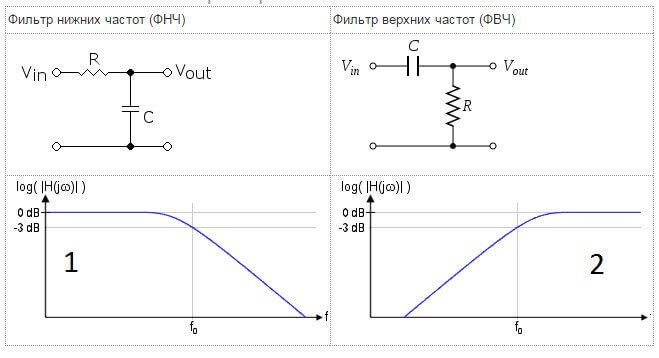 По этому искомую оценку отношения сигнал/шум проведем на примере прямоугольного импульса.
По этому искомую оценку отношения сигнал/шум проведем на примере прямоугольного импульса.
(3.4)
Рис.1
Будем считать, что полезный сигнал представляет собой одиночный прямоугольный импульс (3.4) длительностью и с напряжением , изображенный на рис 1.
Его спектральная плотность описывается функцией
и сопряженнаяследовательно, для данного импульса в соответствии с (3.3) имеем:
(3.5).Такой коэффициент передачи может быть обеспечен схемой рис 2.
Рис.2
Содержащей идеальное интегрирующее звено (), линию задержки () и схему вычитания .
Найдем сигнал на выходе оптимального фильтра для рассматриваемого примера (=1)
(3.
 6).
6).
Таким образом, импульс на выходе имеет треугольную форму с основанием 2t и максимальным значением U0 при t=t . Оценим теперь мощность шума на выходе этого оптимального фильтра. Используем формулы (3.3) и (3.5). Положим a =1 Будем считать шум ’ белым’.
Рис.3
Представим модуль оптимального коэффициента передачи в виде
(3.7)
Мощность шума на выходе фильтра в соответствии с (2.2 ) и (2.3) определиться так
(3.8).
Этот табличный интеграл [3] имеет значение: . Таким образом, искомая величина мощности шума равна:
откуда искомое отношение мощности сигнала к мощности шума для данного оптимального фильтра будет:
(3.10).а для отношения амплитуд сигнал/шум
(3.11).В заключение еще раз отметим, что оптимальный фильтр, построенный по указанному выше критерию, жестко связан с полезным входным сигналом: изменение полезного входного сигнала ведет к необходимости изменения коэффициента передачи фильтра.
3.3. Определение оптимальной полосы фильтра нижних частот в задаче выделения (обнаружения) одиночного сигнала на фоне белого шума
Учитывая сложность задачи синтеза оптимального фильтра , в результате которого находится его функция можно подойти к задаче по другому.
Сигналу выбирается тип АЧХ фильтра, сообразуясь с формой сигнала-импульса (точнее модулем его спектра). Например, для рассмотренного выше прямоугольного импульса выбирается фильтр НЧ, для импульса с высокочастотным заполнением- резонансный фильтр и т.д. Далее задача оптимизации ставится относительно выбора параметра фильтра — полосы его пропускания. Следуя этому подходу далее рассматривается возможность выделения полезного сигнала из белого шума не с помощью описанного выше оптимального фильтра, а с помощью линейного RC фильтра нижних частот. При этом полоса фильтра будет выбираться таким образом, чтобы достигнуть максимально возможного (для фильтра нижних частот) энергетического соотношения сигнал/шум к концу импульса.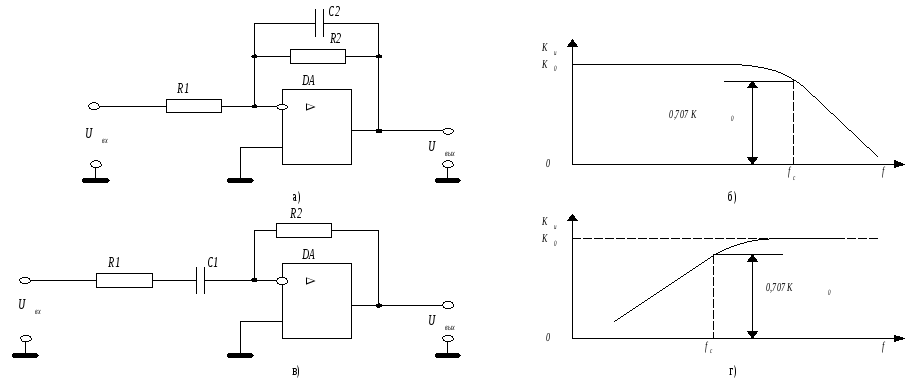
Пусть полный входной сигнал U(t) выражается в виде суммы полезного входного сигнала и белого шума — случайного процесса, у которого спектральная плотность не зависит от частоты
(3.12).
В качестве фильтра нижних частот будем рассматривать интегрирующую цепочку (рис 4) — низкочастотный фильтр первого порядка с постоянной времени и коэффициентом передачи
(3.13).
Рис. 4
При исследовании прохождения шума через линейную систему будем использовать формулу (2.3) ,квадрат модуля коэффициента передачи
(3.14).где — полоса пропускания рассматриваемого фильтра нижних частот по уровню 0.707. Требуется найти полосу заданного фильтра нижних частот, обеспечивающую максимальное отношение сигнал/шум на выходе фильтра.
Можно рассматривать прохождение через фильтр нижних частот полезного сигнала и шума раздельно, так как интегрирующая цепочка — линейная схема.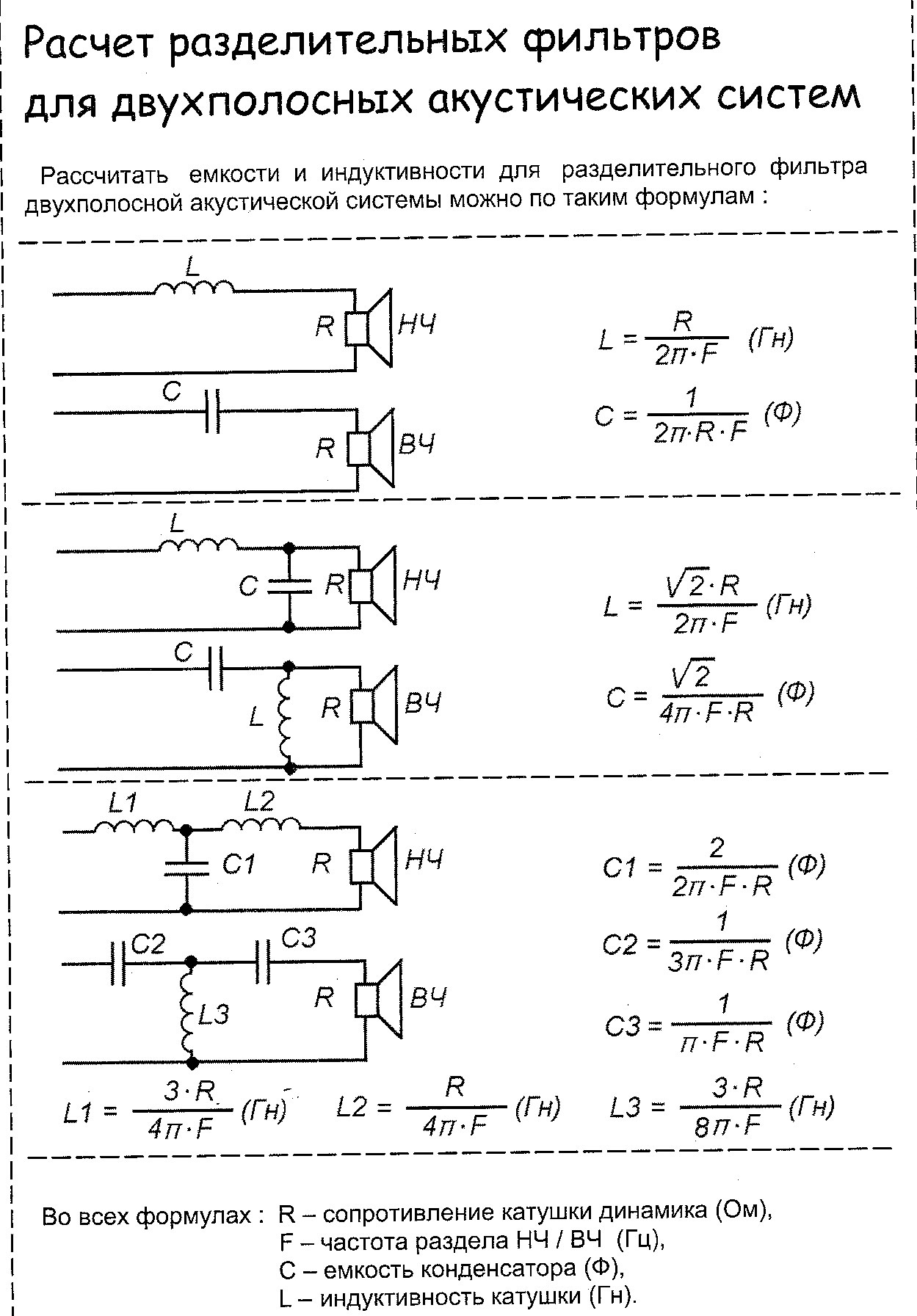
3.3.1. Прохождение полезного сигнала через однозвенный RC фильтр нижних частот
Сигнал на выходе линейной системы может быть найден с помощью спектрального метода.
(3.15).где коэффициент передачи интегрирующей цепочки определяется формулой (3.14) , а спектральная плотность полезного входного сигнала (3.4) была найдена как интеграл Фурье
(3.16).Подставив в (3.15) формулы (3.16) и (3.13) и вычислив интеграл, получаем следующее выражение для сигнала на выходе фильтра
при (3.17)Рис 5.
Таким образом, выходной сигнал достигает своего максимального значения в момент окончания входного импульса t=t
(3.18).Это выражение зависит от соотношения полосы частот фильтра (3.13) и полосы частот, занимаемой полезным сигналом , которая связана с длительностью прямоугольного импульса так 1/t . С учетом этого выражение (3.18) можно преобразовать следующим образом
С учетом этого выражение (3.18) можно преобразовать следующим образом
Если полоса частот, занимаемая спектральной плотностью полезного входного сигнала, меньше полосы частот, определяемой коэффициентом передачи интегрирующей цепочки , то максимальное значение полезного сигнала на выходе интегрирующей цепочки (3.18) равно и не зависит от полосы фильтра при .
Если же полоса частот, занимаемая спектральной плотностью полезного входного сигнала, больше полосы частот, занимаемой коэффициентом передачи интегрирующей цепочки, , то разложив экспоненту в выражении (3.18) в ряд, получаем следующее максимальное значение полезного сигнала на выходе интегрирующей цепочки
В этом случае амплитуда полезного сигнала на выходе фильтра линейно зависит от полосы фильтра .
Мощность полезного входного сигнала, входящая в энергетическое отношение сигнал/шум, будет пропорциональна, таким образом, квадрату от полосы фильтра
Следовательно, если полоса фильтра перекрывает полосу полезного входного сигнала, то дальнейшее увеличение полосы фильтра не приводит к увеличению полезного выходного сигнала. Если же полоса фильтра уже полосы сигнала, то увеличение полосы фильтра приводит к увеличению мощности полезного выходного сигнала, пропорционально квадрату полосы фильтра.
Если же полоса фильтра уже полосы сигнала, то увеличение полосы фильтра приводит к увеличению мощности полезного выходного сигнала, пропорционально квадрату полосы фильтра.
3.3.2. Прохождение случайного сигнала (белого шума) через фильтр нижних частот
Для мощности шума на выходе фильтра с помощью формул (2.2) и (2.3) может быть получено следующее выражение
(3.20),в котором положим — спектральная плотность мощности белого шума, а квадрат модуля коэффициента передачи определен формулой (3.14). Вычислив интеграл , получаем
(3.21),где — ширина полосы фильтра по уровню 1/.
Отсюда следует, что мощность шума на выходе фильтра линейно зависит от полосы коэффициента передачи интегрирующей цепочки.
Используя полученные выражения для максимального значения выходного полезного сигнала (3.18) и мощности шума на выходе фильтра (3. 21), можно получить выражение для энергетического отношения сигнал/шум на выходе фильтра нижних частот (RC-цепочки):
21), можно получить выражение для энергетического отношения сигнал/шум на выходе фильтра нижних частот (RC-цепочки):
где
и (3.23)Искомую величину оптимальной полосы для выбранного НЧ фильтра (3.13) и сигнала (3.4), обеспечивающей максимальное отношение сигнал/шум в момент t=t , найдем из условия максимума функции (3.23), т.е .
(3.24).Функция имеет пологий максимум, ее график приведен на рис 6.
Рис. 6
Таким образом
И следовательно отношение пиковой мощности сигнала и мощности шума при оптимальной полосе НЧ фильтра равно
(3.25).
Отношение же амплитуды сигнала к «амплитуде» шума будет
(3.26).Напомним, что использование фильтра с оптимальным коэффициентом передачи(3.5) приводило к отношению сигнал/шум по мощности равному (3. 10)
10)
Сравнивая (3.10) с (3.25), видим, что использование RC фильтра НЧ (3.13) с правильно выбранной полосой вместо фильтра с оптимальным коэффициентом передачи приводит к ухудшению соотношения сигнал/шум по мощности на 19 %.
(3.27),и лишь на 10% по отношению амплитуд сигнал/шум
(3.28).Т.о. для конкретного сигнала — прямоугольного импульса использование простого RC фильтра НЧ можно считать оправданным (целесообразным).
Качественно такой результат понятен. Если полоса фильтра уже полосы сигнала, то целесообразно увеличивать полосу фильтра, так как при этом мощность полезного сигнала на выходе растет пропорционально квадрату полосы, а мощность шума растет пропорционально первой степени полосы. Если полоса фильтра шире полосы сигнала, то целесообразно уменьшать полосу фильтра, так как при этом мощность полезного сигнала на выходе не меняется, а мощность шума уменьшается пропорционально первой степени полосы.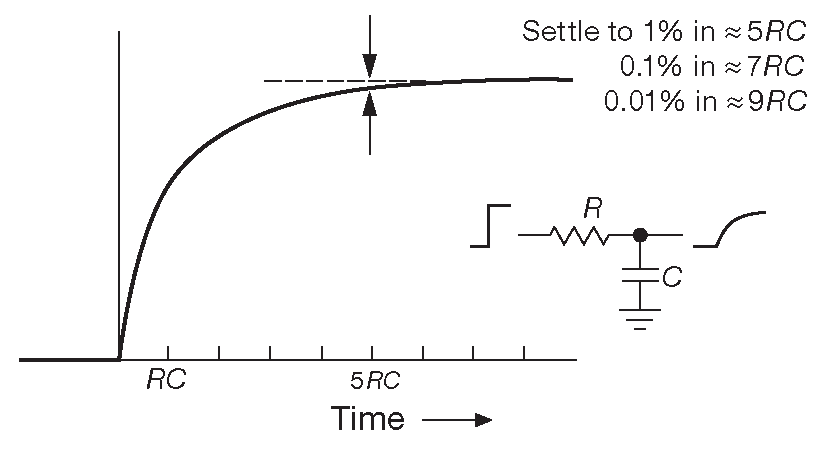
Далее найдем соотношение сигнал/шум для многозвенного RC — фильтра низкой частоты.
3.4 Определение оптимальной полосы многозвенного фильтра нижних частот
Рассмотрим теперь задачу определения оптимальной полосы многозвенного фильтра с целью обеспечения максимального отношения сигнал/шум в момент окончания импульса. Импульс будем, как и раньше, считать прямоугольным.(3.4). Конкретно рассмотрим фильтр, собранный идентичных RC — звеньев, разделенных буферными каскадами.(рис 7).
Рис 7.
Коэффициент передачи такого фильтра описывается функцией
(3.29)
Если зафиксировать полосу пропускания этого фильтра на заданном уровне неравномерности , то эти два параметра, как это следует из (3.29), оказываются связанными уравнением
(3.30).Отсюда очевидно, что для обеспечения постоянства общей заданной полосы фильтра при изменении числа звеньев n, постоянную необходимо изменить следующим образом
(3. 31).
31).
При увеличении числа звеньев n, будет увеличиваться крутизна спада АЧХ в области частот, выше заданной полосы . (рис 8).
Рис8.
Переходная характеристика h(t) для рассматриваемого фильтра (3.29) — реакция на включение ступеньки напряжения на входе определяется так:
(3.32).
где , как отмечено выше, если при увеличении числа каскадов n ставится требование =const ( на заданном уровне неравномерности ), то параметр каждого каскада должен изменятся в соответствии с формулой (3.31). Пример зависимости от n для n=1 и n=5 при одинаковой приведен на рис.8, а зависимость переходной характеристики h(t) также при n=1 и n=5 приведен на рис.9.
Оценим теперь уровень шума на выходе фильтра. Считаем шум на выходе белым, имеющим спектральную плотность мощности S0
(3.
 33).
33).
Значение этого табличного неопределенного интеграла (3.36) известно [ 3].
(3.34).
При вычислении определенного интеграла (3.34) следует учесть, что функция равна нулю на верхнем () и на нижнем (-) пределах. Поэтому
(3.35).Учитывая также необходимое изменение RC каждого каскада фильтра при увеличении n (при требовании =const) получаем интересующий количественный результат. В качестве примера приводим численные данные расчета мощности шума и напряжения шума для фильтров разных порядков (n).
и (3.36).
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
|
0. |
0.78 |
0.85 |
0.9 |
0.95 |
1.01 |
|
|
0.5 |
0.61 |
0.72 |
0.81 |
0.91 |
1.025 |
Полученные выше данные о прохождении импульсного сигнала и белого шума через n-звенныйфильтр низкой частоты позволит определить оптимальную полосу фильтра ( при заданной длительности импульса) и соотношение сигнал/шум на выходе рассматриваемого фильтра в момент окончания импульс t=t при оптимальном выборе его полосы .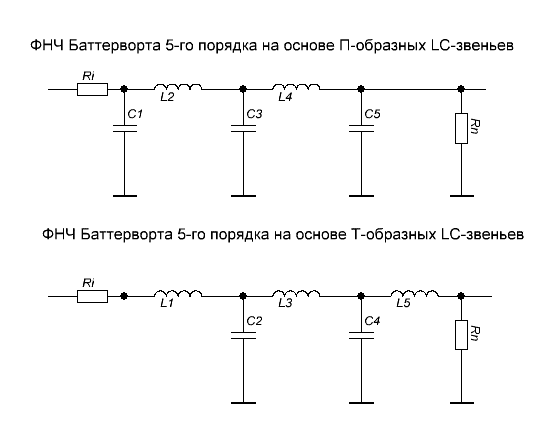 Как и в случае однозвенного фильтра строим функцию отношения величины полученного сигнала к «амплитуде» шума
Как и в случае однозвенного фильтра строим функцию отношения величины полученного сигнала к «амплитуде» шума
Здесь , -коэффициент изменения RC= каждого звена, при изменении порядка фильтра n (3.31)
Отношение , как функция ,имеет пологий max, зависящий от порядка фильтра n.
Так, например, для трехзвенного фильтра max достигается при , и значении . Для пятизвенного фильтра получаем и . Из этих значений определяется оптимальная величина параметра фильтра .
Т.о. искомое отношение амплитуд сигнал/шум с учетом коэффициентов Ki в соответствии с выражением (3.37) дает:
Для трехзвенного фильтра (3.38), Для пятизвенного фильтра (3.39).Сравнивая эти результаты с полученными ранее, видим, что повышение порядка фильтра дает худшее отношение сигнал/шум, чем для фильтра первого порядка (3.13):
и (3.40).
Поэтому, если «оптимальный» фильтр определяемый требованием (см(3.3)) заменяется фильтром RC с оптимально подбираемым параметром, то в рассматриваемом случае прямоугольного импульса лучшим оказывается простейший RC фильтр первого порядка .
Этому предпочтению можно дать следующие объяснения.
Во-первых, АЧХ RC фильтр первого порядка оказывается ближе к модулю спектра прямоугольного импульса, чем АЧХ фильтров более высоких порядков. Напомним, что для «оптимального» фильтра в соответствии с (3.3) оказывается, что его АЧХ совпадает с модулем спектра сигнала.
Во-вторых, как показано выше, значение обобщенного параметра , обеспечивающего наибольшее отношение мощности сигнала к мощности шума в конце импульса, увеличивается с повышением порядка фильтра. Так например, при n=1 значение , при n=3 имеем, что , а при n=5 обобщённый параметр .
Поэтому при заданной длительности импульса t полоса фильтра , требуется большей, для фильтра более высокого порядка, что также приводит к повышению шума.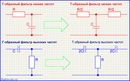
Физически последнюю зависимость от n можно объяснить ростом группового запаздывания, т. е. требуемое максимальное отношение
к концу импульса достигается для больших n при больших значениях . Что при фиксированной длительности импульса означает большее значение . А это , естественно, увеличивает шум на выходе фильтра.
RC цепь | Практическая электроника
R – это резистор, С – конденсатор, а вместе они образуют RC-цепь, то есть это цепь, которая состоит из конденсатора и резистора. Все просто 😉
Принцип работы RC цепи
Как вы помните, конденсатор представляет из себя две обкладки на некотором расстоянии друг от друга.
Вы, наверное, помните, что его емкость зависит от площади обкладок, от расстояния между ними, а также от вещества, которое находится между обкладками. Или формулой для плоского конденсатора:
где
Ладно, ближе к делу. Пусть у нас имеется конденсатор. Что с ним можно сделать? Правильно, зарядить 😉 Для этого берем источник постоянного напряжения и подаем заряд на конденсатор, тем самым заряжая его:
Что с ним можно сделать? Правильно, зарядить 😉 Для этого берем источник постоянного напряжения и подаем заряд на конденсатор, тем самым заряжая его:
В результате, у нас конденсатор зарядится. На одной обкладке будет положительный заряд, а на другой обкладке – отрицательный:
Даже если убрать батарею, у нас заряд на конденсаторе все равно сохранится в течение какого-то времени.
Сохранность заряда зависит от сопротивления материала между пластинами. Чем оно меньше, тем быстрее со временем будет разряжаться конденсатор, создавая ток утечки. Поэтому самыми плохими, в плане сохранности заряда, являются электролитические конденсаторы, или в народе – электролиты:
Но что произойдет, если к конденсатору мы подсоединим резистор?
Конденсатор разрядится, так как цепь станет замкнутой. Разряжаться он будет через резистор. В разряде конденсатора через резистор и заложен весь принцип работы RC цепочки.
Постоянная времени RC-цепи
Но дело в том, что мы не можем наблюдать процесс разрядки конденсатора, просто посмотрев на RC цепь. Для этого нам понадобится цифровой осциллограф с функцией записи сигнала. Благо на моем рабочем столе уже есть место этому прибору:
Итак, план действий будет такой: мы будем заряжать конденсатор с помощью блока питания, а потом разряжать его на резисторе и смотреть осциллограмму, как разряжается конденсатор.
Соберем классическую схему, которая есть в любом учебнике по электронике:
в этот момент мы заряжаем конденсатор
потом переключаем тумблер S в другое положение и разряжаем конденсатор, наблюдая процесс разряда конденсатора на осциллографе
Думаю, с этим все понятно. Ну что же, приступим к сборке.
Берем макетную плату и собираем схемку. Конденсатор я взял емкостью в 100мкФ, а резистор 1 КилоОм.
Вместо тумблера S я буду вручную перекидывать желтый проводок.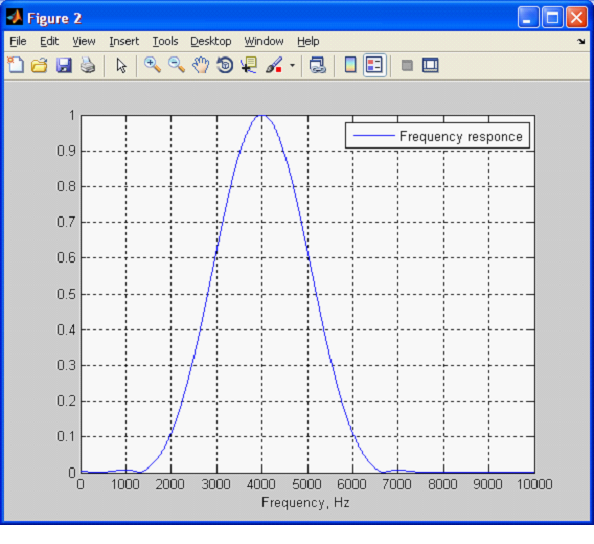
Ну все, цепляемся щупом осциллографа к резистору
и смотрим осциллограмму, как разряжается конденсатор.
Те, кто впервые читает про RC-цепи, думаю, немного удивлены. По логике, разряд должен проходить прямолинейно, но здесь мы видим загибулину. Разряд происходит по так называемой экспоненте. Так как я не люблю алгебру и матанализ, то не буду приводить различные математические выкладки. Кстати, а что такое экспонента? Ну экспонента – это график функции “е в степени икс”. Короче, все учились в школе, вам лучше знать 😉
Так как при замыкании тумблера у нас получилась RC-цепь, то у нее есть такой параметр, как постоянная времени RC-цепи. Постоянная времени RC-цепи обозначается буквой t , в другой литературе обозначают большой буквой T. Чтобы было проще для понимания, давайте также будем обозначать постоянную времени RC цепи большой буквой Т.
Итак, думаю стоит запомнить, что постоянная времени RC-цепи равняется произведению номиналов сопротивления и емкости и выражается в секундах, или формулой:
T=RC
где T – постоянная времени , Секунды
R – сопротивление, Ом
С – емкость, Фарады
Давайте посчитаем, чему равняется постоянная времени нашей цепи.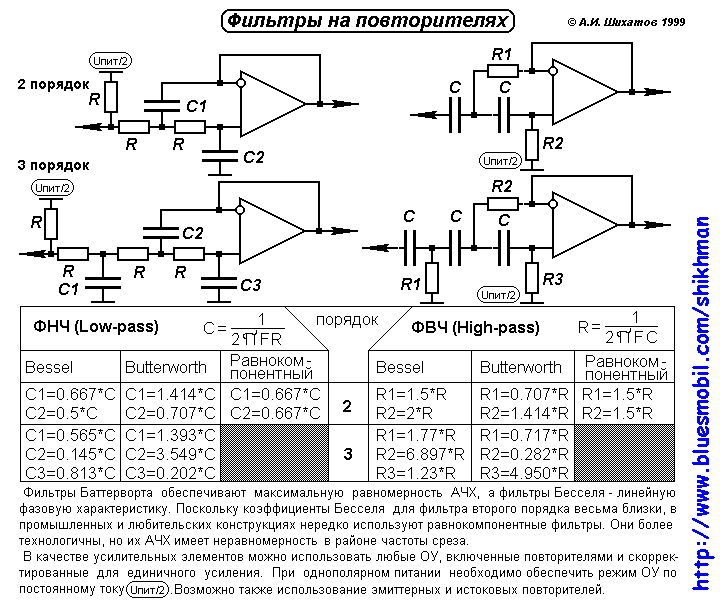 Так как у меня конденсатор емкостью в 100 мкФ, а резистор 1 кОм, то постоянная времени равняется T=100 x 10-6 x 1 х 103 =100 x 10-3 = 100 миллисекунд.
Так как у меня конденсатор емкостью в 100 мкФ, а резистор 1 кОм, то постоянная времени равняется T=100 x 10-6 x 1 х 103 =100 x 10-3 = 100 миллисекунд.
Для тех, кто любит считать глазами, можно построить уровень в 37% от амплитуды сигнала и затем уже аппроксимировать на ось времени. Это и будет постоянная времени RC-цепи. Как вы видите, наши алгебраические расчеты почти полностью сошлись с геометрическими, так как цена деления стороны одного квадратика по времени равняется 50 миллисекундам.
В идеальном случае конденсатор сразу же заряжается, если на него подать напряжение. Но в реальном все-таки есть некоторое сопротивление ножек, но все равно можно считать, что заряд происходит почти мгновенно. Но что будет, если заряжать конденсатор через резистор? Разбираем прошлую схему и стряпаем новую:
исходное положение
как только мы замыкаем ключ S, у нас конденсатор начинает заряжаться от нуля и до значения 10 Вольт, то есть до значения, которое мы выставили на блоке питания
Наблюдаем осциллограмму, снятую с конденсатора
Ничего общего не увидели с прошлой осциллограммой, где мы разряжали конденсатор на резистор? Да, все верно. Заряд тоже идет по экспоненте ;-). Так как радиодетали у нас одинаковые, то и постоянная времени тоже одинаковая. Графическим способом она высчитывается как 63% от амплитуды сигнала
Заряд тоже идет по экспоненте ;-). Так как радиодетали у нас одинаковые, то и постоянная времени тоже одинаковая. Графическим способом она высчитывается как 63% от амплитуды сигнала
Как вы видите, мы получили те же самые 100 миллисекунд.
По формуле постоянной времени RC-цепи, нетрудно догадаться, что изменение номиналов сопротивления и конденсатора повлечет за собой изменение и постоянной времени. Поэтому, чем меньше емкость и сопротивление, тем короче по времени постоянная времени. Следовательно, заряд или разряд будет происходить быстрее.
Для примера, давайте поменяем значение емкости конденсатора в меньшую сторону. Итак, у нас был конденсатора номиналом в 100 мкФ, а мы поставим 10 мкФ, резистор оставляем такого же номинала в 1 кОм. Посмотрим еще раз на графики заряда и разряда.
Вот так заряжается наш конденсатор номиналом в 10 мкФ
А вот так он разряжается
Как вы видите, постоянная времени цепи в разы сократилась. Судя по моим расчетам она стала равняться T=10 x 10-6 x 1000 = 10 x 10-3 = 10 миллисекунд. Давайте проверим графо-аналитическим способом, так ли это?
Давайте проверим графо-аналитическим способом, так ли это?
Строим на графике заряда или разряда прямую на соответствующем уровне и аппроксимируем ее на ось времени. На графике разряда будет проще 😉
Одна сторона квадратика по оси времени у нас 10 миллисекунд (чуть ниже рабочего поля написано M:10 ms), поэтому нетрудно посчитать, что постоянная времени у нас 10 миллисекунд ;-). Все элементарно и просто.
То же самое можно сказать и про сопротивление. Емкость я оставляю такой же, то есть 10 мкФ, резистор меняю с 1 кОм на 10 кОм. Смотрим, что получилось:
По расчетам постоянная времени должна быть T=10 x 10-6 x 10 x 103 = 10 x 10-2 = 0,1 секунда или 100 миллисекунд. Смотрим графо-аналитическим способом:
100 миллисекунд 😉
Вывод: чем больше номинал конденсатора и резистора, тем больше постоянная времени, и наоборот, чем меньше номиналы этих радиоэлементов, тем меньше постоянная времени. Все просто 😉
Все просто 😉
Ладно, думаю, с этим все понятно. Но куда можно применить этот принцип зарядки и разрядки конденсатора? Оказывается, применение нашлось…
[quads id=1]
Интегрирующая RC цепь
Собственно сама схема:
А что будет, если мы на нее будем подавать прямоугольный сигнал с разной частотой? В дело идет китайский генератор функций:
Выставляем на нем частоту 1 Герц и размахом в 5 Вольт
Желтая осциллограмма – это сигнал с генератора функций, который подается на вход интегрирующей цепи на клеммы Х1, Х2, а с выхода мы снимаем красную осциллограмму, то есть с клемм Х3, Х4:
Как вы могли заметить, конденсатор почти полностью успевает зарядиться и разрядиться.
Но что будет, если мы добавим частоту? Выставляю на генераторе частоту в 10 Герц. Смотрим что у нас получилось:
Конденсатор не успевает заряжаться и разряжаться как уже приходит новый прямоугольный импульс. Как мы видим, амплитуда выходного сигнала очень сильно просела, можно сказать, он скукожился ближе к нулю.
Как мы видим, амплитуда выходного сигнала очень сильно просела, можно сказать, он скукожился ближе к нулю.
А сигнал в 100 Герц вообще не оставил ничего от сигнала, кроме малозаметных волн
Сигнал в 1 Килогерц на выходе вообще не дал ничего…
Еще бы! Попробуй-ка с такой частотой перезаряжать конденсатор 🙂
Все то же самое касается и других сигналов: синусоиды и треугольного. везде выходной сигнал почти равен нулю на частоте 1 Килогерц и выше.
“И это все, на что способна интегрирующая цепь?” – спросите вы. Конечно нет! Это было только начало.
Давайте разберемся… Почему у нас с возрастанием частоты сигнал стал прижиматься к нулю и потом вообще пропал?
Итак, во-первых, эта цепь у нас получается как делитель напряжения, и во-вторых, конденсатор – это частотно-зависимый радиоэлемент. Его сопротивление зависит от частоты. Про это можно прочитать в статье конденсатор в цепи постоянного и переменного тока. Следовательно, если бы мы подавали постоянный ток на вход (у постоянного тока частота 0 Герц), то и на выходе бы тоже получили тот же самый постоянный ток такого же значения, которое загоняли на вход. В это случае конденсатору ведь по барабану. Все что он сможет сделать в этой ситуации – тупо зарядиться по экспоненте и все. На этом его участь в цепи постоянного тока заканчивается и он стает диэлектриком для постоянного тока.
В это случае конденсатору ведь по барабану. Все что он сможет сделать в этой ситуации – тупо зарядиться по экспоненте и все. На этом его участь в цепи постоянного тока заканчивается и он стает диэлектриком для постоянного тока.
Но как только в цепь подается переменный сигнал, конденсатор вступает в игру. Тут его сопротивление уже зависит от частоты. И чем она больше, тем меньшим сопротивлением обладает конденсатор. Формула сопротивления конденсатора от частоты:
где
ХС – это сопротивление конденсатора, Ом
π – постоянная и равняется приблизительно 3,14
F – частота, Герц
С – емкость конденсатора, Фарад
Итак, что в результате получается? А получается то, что чем больше частота, тем меньше сопротивление конденсатора. На нулевой частоте у нас сопротивление конденсатора в идеале стает равно бесконечности (поставьте в формулу 0 Герц частоту). А так как у нас получился делитель напряжения
следовательно, на меньшем сопротивлении падает меньшее напряжение. С ростом частоты сопротивление конденсатора очень сильно уменьшается и поэтому падение напряжения на нем стает почти 0 Вольт, что мы и наблюдали на осциллограмме.
С ростом частоты сопротивление конденсатора очень сильно уменьшается и поэтому падение напряжения на нем стает почти 0 Вольт, что мы и наблюдали на осциллограмме.
Но на этом ништяки не заканчиваются.
Давайте вспомним, что из себя представляет сигнал с постоянной составляющей. Это есть ничто иное, как сумма переменного сигнала и постоянного напряжения. Взглянув на рисунок ниже, вам все станет ясно.
То есть в нашем случае можно сказать, этот сигнал (ниже на картинке) имеет в своем составе постоянную составляющую, другими словами, постоянное напряжение
Для того, чтобы выделить постоянную составляющую из этого сигнала, нам достаточно прогнать его через нашу интегрирующую цепь. Давайте рассмотрим все это на примере. С помощью нашего генератора функций мы поднимем нашу синусоиду “над полом”, то есть сделаем вот так:
Итак, все как обычно, желтый входной сигнал цепи, красный – выходной. Простая двухполярная синусоида дает нам на выходе RC интегрирующей цепи 0 Вольт:
Чтобы понять, где нулевой уровень сигналов, я их пометил квадратиком:
Теперь давайте я добавлю постоянную составляющую в синусоиду, а точнее – постоянное напряжение, благо это сделать мне позволяет генератор функций:
Как вы видите, как только я поднял синус “над полом”, на выходе цепи я получил постоянное напряжение величиной в 5 Вольт. Именно на 5 Вольт я поднимал сигнал в генераторе функций ;-). Цепочка выделила постоянную составляющую из синусоидального приподнятого сигнала без проблем. Чудеса!
Именно на 5 Вольт я поднимал сигнал в генераторе функций ;-). Цепочка выделила постоянную составляющую из синусоидального приподнятого сигнала без проблем. Чудеса!
Но мы так и не разобрались, почему цепь называется интегрирующей? Кто хорошо учился в школе, в классе эдак 8-9, то наверняка помнит геометрический смысл интеграла – это есть ничто иное, как площадь под кривой.
Давайте рассмотрим тазик с кубиками льда в двухмерной плоскости:
Что будет, если весь лед растает и превратится в воду? Все верно, вода ровным слоем покроет тазик одной плоскостью:
Но какой будет этот уровень воды? Вот именно – средний. Это среднее значение этих башен из кубиков льда. Так вот, интегрирующая цепочка делает то же самое! Тупо усредняет значение сигналов до одного постоянного уровня! Можно сказать, усредняет площадь до одного постоянного уровня.
Но самый смак получается тогда, когда мы подаем на вход прямоугольный сигнал. Давайте так и сделаем. Подадим положительный меандр на RC интегрирующую цепь.
Как вы видите, постоянная составляющая меандра равна половине его амплитуды. Думаю, вы уже и сами догадались, если бы представили тазик с кубиками льда). Или просто подсчитайте площадь каждого импульса и размажьте его равномерным слоем по осциллограмме, как гов… как сливочное масло по хлебу 😉
Ну а теперь самое веселое. Сейчас я буду менять скважность нашего прямоугольного сигнала, так как скважность – это ничто иное, как отношение периода на длительность импульса, следовательно, мы будем менять длительность импульсов.
Уменьшаю длительность импульсов
Увеличиваю длительность импульсов
Если никто ничего до сих пор не заметил, просто взгляните на уровень красной осциллограммы и все станет понятно. Вывод: управляя скважностью, мы можем менять уровень постоянной составляющей. Именно этот принцип и заложен в ШИМ (Широтно-Импульсной Модуляции). О ней как-нибудь поговорим в отдельной статье.
[quads id=1]
Дифференцирующая RC цепь
Еще одно ругательное слово, которое пришло с математики – дифференцирующий. Башка начинает сразу же болеть от одного только их произношения. Но, куда деваться? Электроника и математика неразлучные друзья.
Башка начинает сразу же болеть от одного только их произношения. Но, куда деваться? Электроника и математика неразлучные друзья.
А вот и сама дифференциальная цепочка
В схеме мы только переставили резистор и конденсатор местами
Ну а теперь проведем также все опыты, как мы делали с интегрирующей цепью. Для начала подаем на вход дифференциальной цепи низкочастотный двухполярный меандр с частотой в 1,5 Герца и с размахом в 5 Вольт. Желтый сигнал – это сигнал с генератора частоты, красный – с выхода дифференциальной цепочки:
Как вы видите, конденсатор успевает почти полностью разрядится, поэтому у нас получилась вот такая красивая осциллограмма.
Давайте увеличим частоту до 10 Герц
Как видите, конденсатор не успевает разрядиться, как уже приходит новый импульс.
Сигнал в 100 Герц сделал кривую разряда еще менее заметной.
Ну и добавим частоту до 1 Килогерца
Какой на входе, такой и на выходе 😉 С такой частотой конденсатор вообще не успевает разряжаться, поэтому вершинки выходных импульсов гладкие и ровные.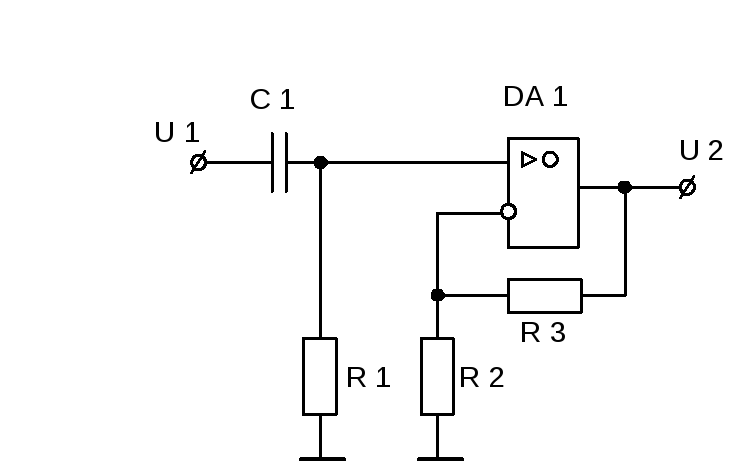
Но и на этом тоже ништяки не заканчиваются.
Давайте я подниму входной сигнал над “уровнем моря”, то есть выведу его в положительную часть полностью. Смотрим, что получается на выходе (красный сигнал)
Ничего себе, красный сигнал по форме и по положению остался таким же, посмотрите – в нем нет постоянной составляющей, как в желтом сигнале, который мы подавали из нашего генератора функций.
Могу даже желтый сигнал вывести в отрицательную область, но на выходе мы все равно получим переменную составляющую сигнала без всяких хлопот:
Да и вообще пусть сигнал будет с небольшой отрицательной постоянной составляющей, все равно на выходе мы получим переменную составляющую:
Все то же самое касается и любых других сигналов:
В результате опытов мы видим, что основная функция дифференциальной цепи – это выделение переменной составляющей из сигнала, который содержит в себе как переменную, так и постоянную составляющую.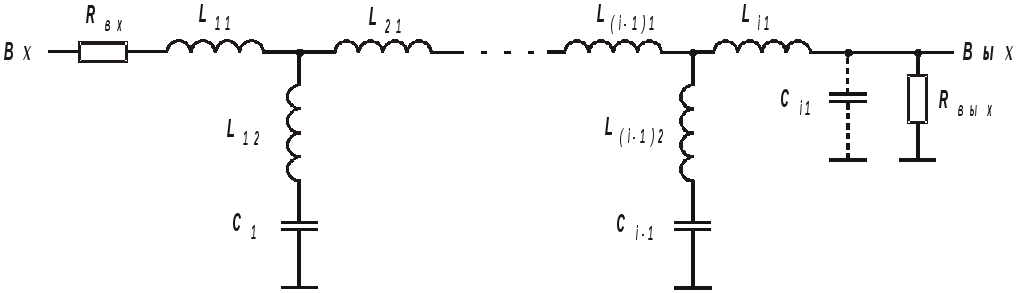 Иными словами – выделение переменного тока из сигнала, который состоит из суммы переменного тока и постоянного тока.
Иными словами – выделение переменного тока из сигнала, который состоит из суммы переменного тока и постоянного тока.
Почему так происходит? Давайте разберемся. Рассмотрим нашу дифференциальную цепь:
Если внимательно рассмотреть эту схему, то мы можем увидеть тот же самый делитель напряжения, как и в интегрирующей цепи. Конденсатор – частотно-зависимый радиоэлемент. Итак, если подать сигнал с частотой в 0 Герц (постоянный ток), то у нас конденсатор тупо зарядится и потом вообще перестанет пропускать через себя ток. Цепь будет в обрыве. Но если мы будем подавать переменный ток, то и через конденсатор он тоже начнет проходить. Чем больше частота – тем меньше сопротивление конденсатора. Следовательно, весь переменный сигнал будет падать на резисторе, с которого мы как раз и снимаем сигнал.
Но если мы будем подавать смешанный сигнал, то есть переменный ток + постоянный ток, то на выходе мы получим просто переменный ток. В этом мы с вами уже убеждались на опыте. Почему так произошло? Да потому что конденсатор не пропускает через себя постоянный ток!
Видео “Как работает RC-цепь РЕАЛЬНО. Понятное объяснение”
Заключение
Интегрирующую цепь также называют фильтром низких частот (ФНЧ), а дифференцирующую – фильтром высоких частот (ФВЧ). Более подробно про фильтры читаем здесь. Чтобы точнее их сделать, нужно провести расчет на нужную вам частоту. RC цепи используются везде, где надо выделить постоянную составляющую (ШИМ), переменную составляющую (межкаскадное соединение усилителей), выделить фронт сигнала, сделать задержку и тд… По мере глубины погружения в электронику вы будете часто встречаться с ними.
Lc фильтр питания расчет
В статье речь пойдёт про расчёт простейших фильтрующих цепей для сглаживания широтно-импульсной модуляции. Что такое ШИМ, где он применяется и как его реализовать читайте в отдельной статье.
Первое, на чём следует заострить внимание — это назначение цепи, для которой вы собрались строить фильтр.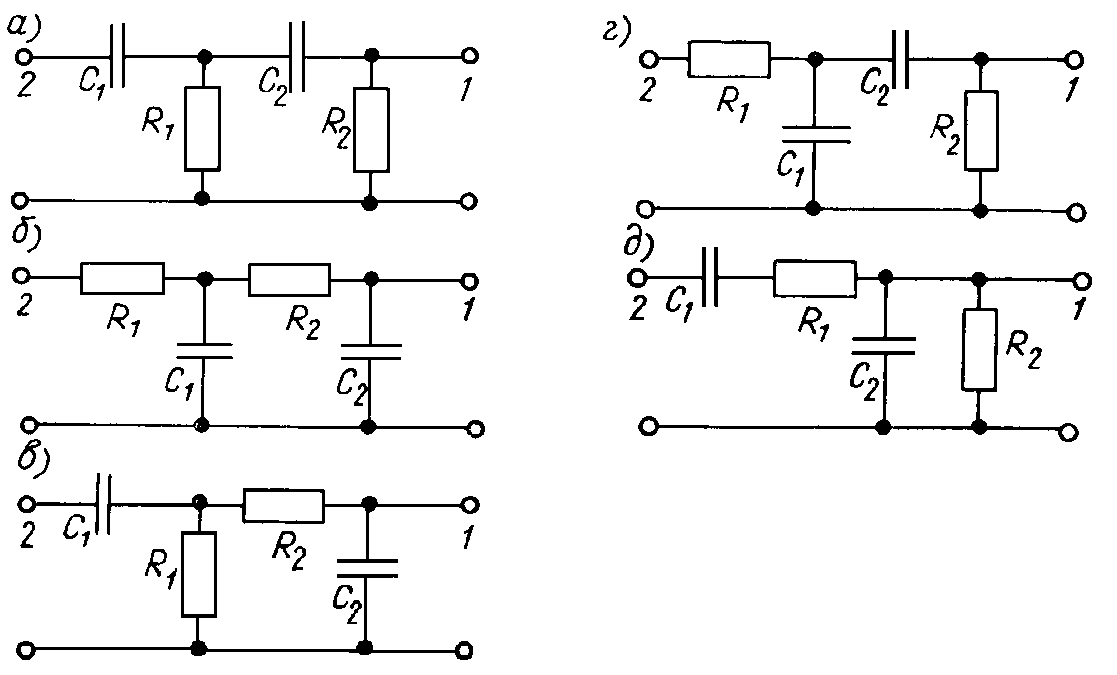 Немного упрощая схемы с ШИМ можно поделить на два типа:
Немного упрощая схемы с ШИМ можно поделить на два типа:
- Сигнальные цепи с ШИМ
- Силовые цепи с ШИМ
Примером сигнального ШИМ служит, например, простейший ЦАП, под силовым ШИМ чаще всего имеется ввиду ШИМ-сигнал на выходе силовых ключей, например в импульсных источниках питания (ИИП). Строго говоря, в источниках питания сам сигнал ШИМ тоже используется в сигнальной цепи (управление транзисторами) и на выходе таких источников сигнал повторяет форму управляющих сигналов, однако имеет более высокую мощность, потому они требуют фильтров позволяющих пропускать большие мощности.
Фильтрация ШИМ в сигнальных цепях
Рис.1. Простейший фильтр нижних частот — интегрирующая RC-цепь и её АЧХ.
Основная характеристика фильтра это частота среза (на рисунке 1 обозначена угловая частота среза — ωс) — амплитуда колебаний данной данной частоты на выходе фильтра ослабляется до уровня
0.707 (-3 Дб) от входного значения.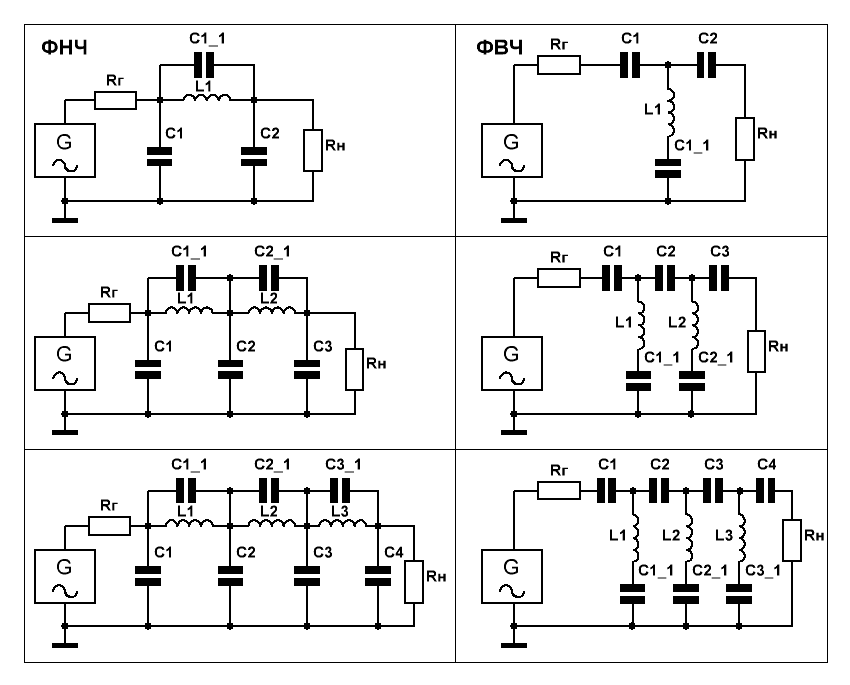 Частота среза определяется по следующей формуле:
Частота среза определяется по следующей формуле:
Тут R и С — сопротивление резистора в омах и ёмкость конденсатора в фарадах. Необходимо помнить, что для корректной работы сглаживающего фильтра постоянная времени RC-цепочки (τ = R · C) должна быть как можно меньше периода ШИМа, тогда за один период не будет происходить полный заряд-разряд конденсатора.
Следующий важный параметр, позволяющий расчитать ослабление колебаний на заданной частоте это коэффициент передачи фильтра — это отношение K = Uвых/Uвх. Для данной RC-цепочки коэффициент передачи рассчитывается следующим образом:
Зная эти формулы и учтя постоянное падение напряжения на резисторе можно приближённо рассчитать фильтр с нужными характеристиками — например, задавшись имеющейся ёмкостью, либо необходимым уровнем пульсаций.
Калькулятор ШИМ-фильтра на RC-цепочке
| Входные данные: | Расчётные значения: |
| Частота ШИМ | Гц |
| Коэффициент заполнения ШИМ (duty cycle) | % |
| Напряжение на входе | В |
| Сопротивление резистора фильтра | Ом |
| Сопротивление нагрузки Rн | Ом |
| Ёмкость конденсатора | мкФ |
(с учётом потерь на резисторе фильтра)
Постоянная времени RC-цепи
Постоянная времени цепи (R · C) не должна быть сильно меньше периода ШИМ!
(не менее)
Обратите внимание — если вы хотите получать из ШИМ-сигнала сглаженный синусоидальный сигнал, необходимо чтобы частота среза фильтра была выше максимальной частоты сигнала, а значит частота ШИМ должна быть ещё выше.
Фильтрация ШИМ в силовых цепях
Рис.2. Фильтр нижних частот на LC-контуре и его АЧХ.
LC-фильтр представляет из себя элементарный колебательный контур, который имеет собственную частоту резонанса, поэтому его реальная АЧХ будет несколько отличаться от АЧХ, приведённой на рисунке 2.
Поскольку речь в данной статье идёт о фильтре для силовых цепей, при расчёте фильтра нужно учитывать, что основная гармоника входящего напряжения тоже должна ослабляться фильтром, следовательно, его резонансная частота должна быть ниже частоты ШИМ.
Формула для расчёта частоты резонанса LC-контура:
f = 1/(2 · π · (L · C) 0.5 )
Если частота резонанса контура совпадёт с частотой ШИМ, LC-контур может перейти в режим генерации, тогда на выходе может случиться конфуз, посему предлагаю вам данного недоразумения тщательно избегать. Кроме того, при проектировании данного фильтра есть ещё несколько нюансов, которые неплохо бы соблюдать для получения желаемого результата, а именно:
- Для исключения резонансных явлений на одной из высокочастотных гармонических составляющих ёмкость конденсатора желательно находить из условия равенства волнового сопротивления фильтра сопротивлению нагрузки:
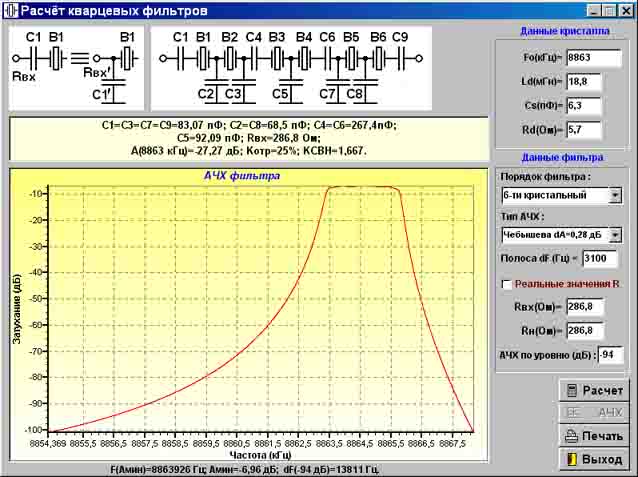
Комплексный коэффициент передачи LC-фильтра рассчитывается по следующей формуле:
где n — номер гармонической составляющей входного сигнала, i — мнимая единица, ω = 2πf, L — индуктивность дросселя (Гн), C — ёмкость конденсатора (Ф), R — сопротивление нагрузки (Ом).
Из формулы очевидно, что чем выше гармоника, тем лучше она подавляется фильтром, следовательно, достаточно рассчитывать уровень только для первой гармоники.
Чтобы перейти от комплексного представления коэффициента передачи к показательному, нужно найти модуль комплексного числа. Для тех, кто (как и я) спал на парах матана в институте, напомню, модуль комплексного числа считается очень просто:
r = |Z| = (x 2 + y 2 ) 0.5
Так как у нас в формуле коэффициента дробь, просто так сходу посчитать модуль не получится и проще всего посчитать это всё, например в MathCad’е. А для тех, кому лень делать всё самим, я запилил весь расчёт в этот прекрасный калькулятор. Пользуйтесь:
Калькулятор силового ШИМ-фильтра на LC-контуре
| Частота ШИМ | Гц |
| Коэффициент заполнения ШИМ (duty cycle) | % |
| Напряжение на входе | В |
| Сопротивление нагрузки | Ом |
| Индуктивность катушки | мГн |
| Ёмкость конденсатора | мкФ |
| Амплитуда пульсаций на частоте ШИМ | В | Резонансная частота контура | Гц |
| Напряжение на выходе (потери не учитываются) | В |
Обратите внимание — при использовании LC-фильтра следует помнить, что из-за наличия в цепи индуктивности, на выходе могут появляться выбросы обратной полярности. Если полярность импульсов на входе не изменяется (например для изменения направления вращения двигателя) для ограничения амлитуды отрицательных выбросов параллельно конденсатору (?) можно включать диод Шоттки.
Если полярность импульсов на входе не изменяется (например для изменения направления вращения двигателя) для ограничения амлитуды отрицательных выбросов параллельно конденсатору (?) можно включать диод Шоттки.
Расчет LC фильтров начинают с определения порядка и сопротивления нагрузки, затем элементы LC фильтра определяют умножением значений фильтра-прототипа на частоту среза. Элементы фильтров-прототипов рассчитаны заранее и сведены в таблицы. Наиболее полные таблицы приведены в справочнике по расчету LC фильтров Р. Зааля [3] В таблице 1 приведены элементы фильтра Баттерворта с частотой среза, равной 1 Гц и сопротивлением 1 Ом.
Таблица 1. Элементы ФНЧ прототипа Баттерворта
| Порядок фильтра | C1 (мФ) | L1 (мГн) | C2 (мФ) | L2 (мГн) | C3 (мФ) | L3 (мГн) | C4 (мФ) | L4 (мГн) | C5 (мФ) | L5 (мГн) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 225,08 | 225,08 | — | — | — | — | — | — | — | — |
| 3 | 159,15 | 318,31 | 159,15 | — | — | — | — | — | — | — |
| 4 | 121,81 | 294,08 | 294,08 | 121,81 | — | — | — | — | — | — |
| 5 | 98,363 | 257,52 | 318,31 | 257,52 | 98,363 | — | — | — | — | — |
| 6 | 82,385 | 225,08 | 307,46 | 307,46 | 225,08 | 82,385 | — | — | — | — |
| 7 | 70,831 | 198,46 | 286,79 | 318,31 | 286,79 | 198,46 | 70,831 | — | — | — |
| 8 | 62,099 | 176,84 | 264,67 | 312,19 | 312,19 | 264,67 | 176,84 | 62,099 | — | — |
| 9 | 55,274 | 159,15 | 243,84 | 299,11 | 318,31 | 299,11 | 243,84 | 159,15 | 55,274 | — |
| 10 | 49,795 | 144,51 | 225,08 | 283,62 | 314,39 | 314,39 | 283,62 | 225,08 | 144,51 | 49,795 |
Схемы LC фильтров Баттерворта от второго до пятого порядка приведены на рисунке 1.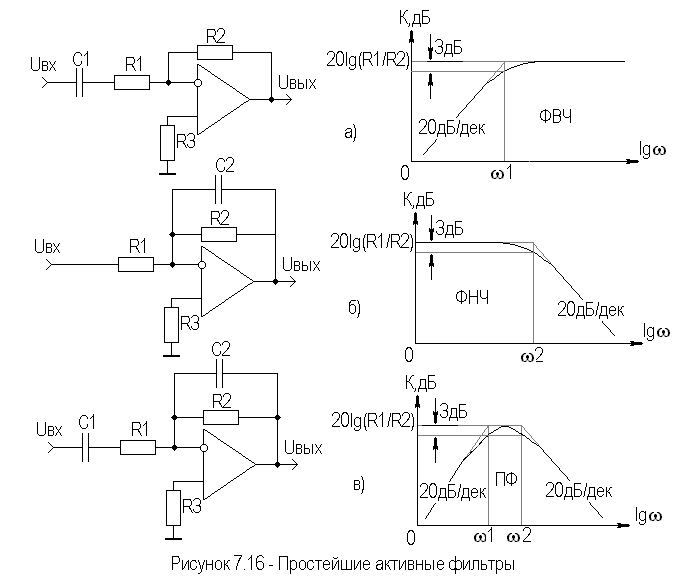 Номиналы их элементов соответствуют частоте 1 Гц.
Номиналы их элементов соответствуют частоте 1 Гц.
Рисунок 1. Схемы П-образных фильтров Баттерворта
После определения фильтра-прототипа производится преобразование входного и выходного сопротивления фильтра. Для увеличения сопротивления LC фильтра значения индуктивностей увеличиваются, а значения емкостей конденсаторов уменьшаются, как это показано в следующей формуле:
(1),
где KZ это отношение сопротивлений рассчитываемого LC фильтра и фильтра-прототипа
И завершается расчет LC фильтра увеличением частоты среза до требуемой величины. Для этого значения индуктивностей и конденсаторов уменьшаются на соответствующий коэффициент:
(2),
Точно таким же образом можно рассчитать и LC фильтр Чебышева. Таблицы L и C элементов фильтров Чебышева с полосой пропускания 1 Гц и сопротивлением 1 Ом приведены ниже:
Таблица 2. Элементы ФНЧ прототипа Чебышева с неравномерностью 0.1 дБ
| Порядок фильтра | C1 (мФ) | L1 (мГн) | C2 (мФ) | L2 (мГн) | C3 (мФ) | L3 (мГн) | C4 (мФ) | L4 (мГн) | C5 (мФ) |
|---|---|---|---|---|---|---|---|---|---|
| 3 | 164,18 | 182,61 | 164,18 | — | — | — | — | — | — |
| 5 | 182,52 | 218.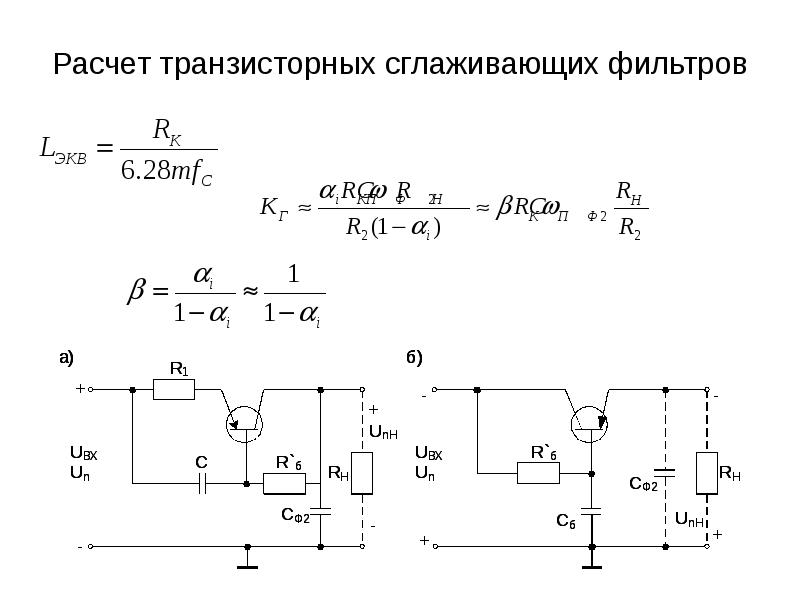 23 23 | 314.33 | 218.23 | 182,52 | — | — | — | — |
| 7 | 187,99 | 226,45 | 333,70 | 250.41 | 333,70 | 226,45 | 187,99 | — | — |
| 9 | 190.30 | 229,60 | 339.73 | 257.31 | 351.00 | 257.31 | 339.73 | 229,60 | 190.30 |
Таблица 3. Элементы ФНЧ прототипа Чебышева с неравномерностью 0.5 дБ
| Порядок фильтра | C1 (мФ) | L1 (мГн) | C2 (мФ) | L2 (мГн) | C3 (мФ) | L3 (мГн) | C4 (мФ) | L4 (мГн) | C5 (мФ) |
|---|---|---|---|---|---|---|---|---|---|
| 3 | 254,06 | 174,54 | 254,06 | — | — | — | — | — | — |
| 5 | 271,50 | 195.70 | 404.39 | 195. 70 70 | 271,50 | — | — | — | — |
| 7 | 276,51 | 200,25 | 419,91 | 213.95 | 419,91 | 200,25 | 276,51 | — | — |
| 9 | 278.60 | 201,97 | 424.60 | 217.61 | 433.53 | 217.61 | 424.60 | 201,97 | 278.60 |
Таблица 4. Элементы ФНЧ прототипа Чебышева с неравномерностью 3 дБ
| Порядок фильтра | C1 (мФ) | L1 (мГн) | C2 (мФ) | L2 (мГн) | C3 (мФ) | L3 (мГн) | C4 (мФ) | L4 (мГн) | C5 (мФ) |
|---|---|---|---|---|---|---|---|---|---|
| 3 | 533,00 | 113,27 | 533,00 | — | — | — | — | — | — |
| 5 | 554,10 | 121.26 | 722.21 | 121.26 | 554,10 | — | — | — | — |
| 7 | 560,02 | 122,89 | 738,35 | 127.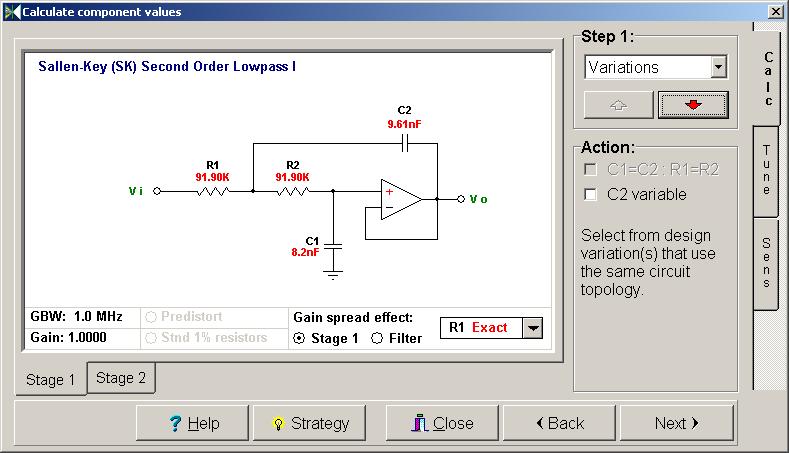 92 92 | 738,35 | 122,89 | 560,02 | — | — |
| 9 | 562.48 | 123,50 | 743.14 | 129.20 | 752.37 | 129.20 | 743.14 | 123,50 | 562.48 |
В таблицах приведены только фильтры нечетных порядков. Это связано с тем, что у LC фильтров Чебышева четных порядков входное и выходное сопротивление не могут быть равны. Рассмотрим пример проектирования LC фильтра.
Пример 1 Расчет LC фильтра низких частот
Задание Спроектировать фильтр нижних частот, пропускающий сигнал с частотами ниже и подавляющий помехи с частотами выше на . Неравномерность АЧХ в полосе пропускания . Входное и выходное сопротивление фильтра должно быть равно . Подобные фильтры часто применяются в качестве антиалиайсинговых фильтров на входе аналого-цифровых преобразователей.
1) Рассчитаем расстройку по частоте на частоте подавления помех.
,
2) Определим порядок фильтра и тип аппроксимации АЧХ. Так как дополнительных требований к фильтру не задано, выберем фильтр с максимальной крутизной АЧХ — фильтр Чебышева с неравномерностью 3 дБ. Фильтр Чебышева третьего порядка обеспечит при отстройке по частоте ξ=2 подавление сигнала на 28 дБ, что недостаточно (аппроксимация по Чебышеву, рисунок 6). Фильтр Чебышева пятого порядка обеспечит подавление помех на , поэтому именно его и выберем. Схема фильтра-прототипа Чебышева 5-порядка показана на рисунке 2.
Так как дополнительных требований к фильтру не задано, выберем фильтр с максимальной крутизной АЧХ — фильтр Чебышева с неравномерностью 3 дБ. Фильтр Чебышева третьего порядка обеспечит при отстройке по частоте ξ=2 подавление сигнала на 28 дБ, что недостаточно (аппроксимация по Чебышеву, рисунок 6). Фильтр Чебышева пятого порядка обеспечит подавление помех на , поэтому именно его и выберем. Схема фильтра-прототипа Чебышева 5-порядка показана на рисунке 2.
Рисунок 2. Схема фильтра-прототипа на LC элементах
3) Согласуем вход и выход фильтра с волновым сопротивлением . Для этого воспользуемся выражением (1). Новые значения емкостей уменьшатся в , а значения индуктивностей увеличатся на это же значение. Преобразованная схема фильтра приведена на рисунке 3.
Рисунок 3. Схема 50-омного фильтра низких частот с частотой среза 1 Гц
И, наконец, уменьшим значения индуктивностей и емкостей в миллион раз, чтобы частота среза фильтра стала равной . Окончательная схема разработанного фильтра низкой частоты, пропускающего сигналы в полосе и подавляющего помехи в полосе непропускания на приведена на рисунке 4.
Рисунок 4. Схема рассчитанного LC фильтра низких частот с частотой среза 1 МГц
После этого можно приступать к проектированию конструкции фильтра. До недавнего времени при проектировании фильтра выбирались только конденсаторы, а индуктивности изготавливались самостоятельно. В последнее время появилась возможность покупать не только конденсаторы, но и индуктивности. Ряд фирм предоставляет готовые индуктивности с заданными параметрами.
Пример 2 Расчет полосового LC фильтра
Задание Спроектировать полосовой фильтр с центральной частотой f, равной . Полоса пропускания равна , неравномерность в полосе пропускания . Коэффициент прямоугольности равен 2, подавление в полосе непропускания . Входное и выходное сопротивление фильтра должно быть равно . Подобные фильтры часто применяются в качестве входных фильтров радиоприемников.
1) Сначала определим узкополосный или широкополосный полосовой фильтр нам задан. Для этого поделим полосу пропускания фильтра на его центральную частоту.
,
Так как относительная ширина полосы пропускания получилась меньше 10%, то полосовой фильтр узкополосный, и его не имеет смысла выполнять в виде отдельных ФНЧ и ФВЧ.
2) Формула определения коэффициента прямоугольности фильтра совпадает с формулой определения отстройки по частоте для полосы задерживания ФНЧ прототипа, поэтому запишем ξз=2.
3) Теперь определим порядок фильтра-прототипа, необходимый для обеспечения подавления мешающего сигнала на . По графику амплитудно-частотной характеристики фильтра Чебышева пятого порядка определим, что он на частоте отстройки, равной двум, как раз обеспечивает подавление . Поэтому схема фильтра-прототипа будет выглядеть так же, как и в предыдущем примере:
Рисунок 5. Схема фильтра-прототипа пятого порядка
4) Следующий этап — это увеличение полосы пропускания фильтра до и увеличение входного и выходного сопротивления до . Для этого нужно пересчитать индуктивности и конденсаторы фильтра:
,
Дата последнего обновления файла 08. 04.2019
04.2019
Вместе со статьёй “Расчет LC фильтров” читают:
Ёмкостные, индуктивно-ёмкостные, активные сглаживающие фильтры.
Схемы, свойства, онлайн калькулятор.
Потолковали мы основательно на предыдущей странице про разные виды диодных выпрямителей, перебросились парой фраз на тему простейших ёмкостных фильтров, а вопрос достижения параметра коэффициента пульсаций Кп в пределах 10 -5 . 10 -4 так и повис в воздухе — уж очень немалым получается номинал ёмкости сглаживающего конденсатора.
Коэффициент пульсаций выпрямленного напряжения Кп является важнейшим параметром выпрямителя. Его численное значение равно отношению амплитудного значения пульсирующего напряжения к его постоянной составляющей.
Напомню выдержку из печатного издания, приведённую на предыдущей странице:
«Коэффициент пульсаций выбирают самостоятельно в зависимости от предполагаемой нагрузки, допускающей питание постоянным током вполне определённой “чистоты”:
10 -3 .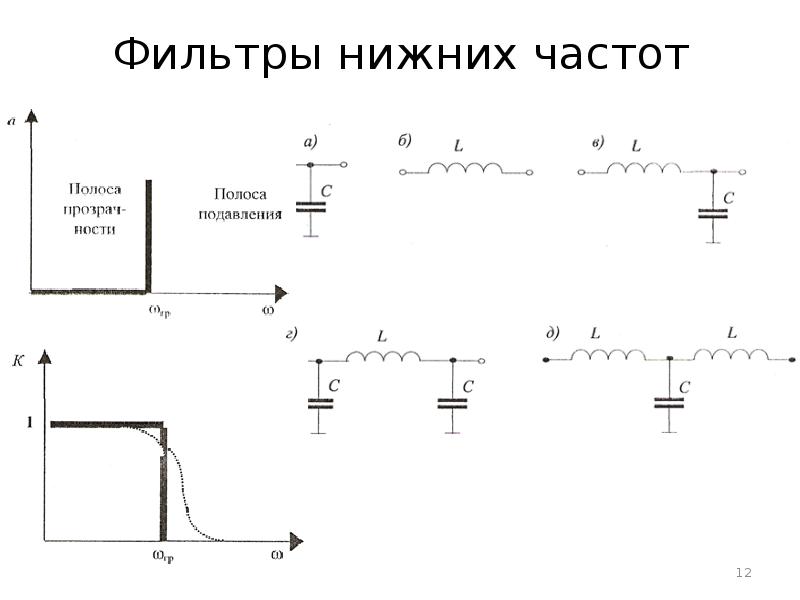 10 -2 (0,1-1%) — малогабаритные транзисторные радиоприёмники и магнитофоны,
10 -2 (0,1-1%) — малогабаритные транзисторные радиоприёмники и магнитофоны,
10 -4 . 10 -3 (0,01-0,1%) — усилители радио и промежуточной частоты,
10 -5 . 10 -4 (0,001-0,01%) — предварительные каскады усилителей звуковой частоты и микрофонных усилителей.»
Помимо этого в характеристиках выпрямителей может использоваться и понятие коэффициента фильтрации (коэффициента сглаживания).
Коэффициент фильтрации, он же коэффициент сглаживания — величина, численно равная отношению коэффициента пульсаций на входе фильтра к коэффициенту пульсаций на выходе фильтра Кс = Кп-вх/Кп-вых .
Для многозвенных фильтров коэффициент фильтрации равен произведению коэффициентов фильтрации отдельных звеньев.
В слаботочных цепях вопрос снижения пульсаций решается легко и кардинально — применением интегральных стабилизаторов. Параметр подавления пульсаций (Ripple Rejection) у подобных массовых ИМС составляет не менее 50дБ (в 360раз по напряжению), что при высокой “чистоте” выходного напряжения позволяет уменьшить ёмкости электролитов в 5-10 раз.
Если же у разработчика нет возможности (либо желания) включать в состав устройства стабилизаторы напряжения, то реальным подспорьем окажутся индуктивно-ёмкостные или активные сглаживающие фильтры.
Начнём с фильтров, выполненных из индуктивных элементов – дросселей и из ёмкостных элементов – конденсаторов.
Рис.1
На Рис.1а приведена схема простейшего ёмкостного сглаживающего фильтра. Принцип действия заключается в накоплении электрической энергии конденсатором фильтра и последующей отдачи этой энергии в нагрузку.
Для того чтобы не ограничиваться 50-ти герцовыми блоками питания, но и иметь возможность расчёта фильтров импульсных ИБП, приведу универсальные формулы, учитывающие частоту входного сигнала F :
С1 = Iн/(3,14×Uн×F×Кп) для однополупериодных выпрямителей и
С1 = Iн/(6,28×Uн×F×Кп) — для двухполупериодных.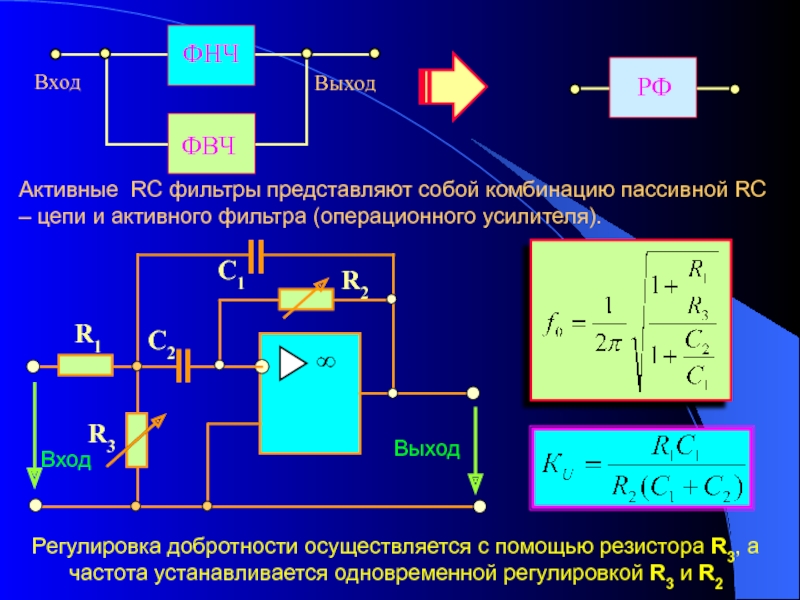
Кп — это коэффициент пульсаций, равный отношению амплитудного значения пульсирующего напряжения к его постоянной составляющей, а
F — частота переменного напряжения на входе диодного выпрямителя.
Переходим к индуктивно-ёмкостным LC фильтрам.
ВНИМАНИЕ. Потребность в такого рода цепях возникает исключительно в случаях необходимости получить низкий уровень пульсаций в достаточно мощных сетевых блоках питания, либо в высокочастотных импульсных ИБП. Связано это с тем, что для эффективной работы LC-фильтра, индуктивное сопротивление катушки XL на частоте подавления стремятся сделать значительно больше Rн. А это, в свою очередь, приводит к тому, что в условиях низких частот и малых токов (высоких Rн) индуктивность дросселя получается необоснованно высокой.
Г-образный индуктивно-ёмкостной LC фильтр 2-го порядка (Рис.1б) обладает значительно лучшими фильтрующими свойствами по сравнению с обычным ёмкостным.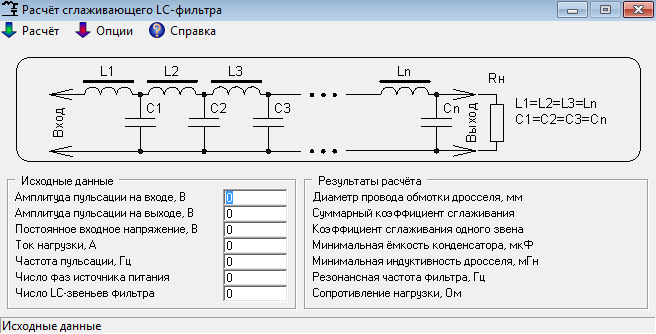
Произведение LC (Гн*мкФ) зависит от необходимого коэффициента сглаживания фильтра и определяется по приближенной формуле:
L1(Гн)×С1(МкФ) = 25000/(F 2 (Гц)×Кп) для однополупериодных выпрямителей и
L1×С1 = 12500/(F 2 ×Кп) — для двухполупериодных, где
С1(МкФ)/L1(мГн) = 1000/Rн 2 (Ом) .
Схема П-образного LC-фильтра приведена на Рис.1в. Сглаживающее действие П-образного LC-фильтра можно упрощённо представить как совместное действие двух фильтров, описанных выше, а коэффициент сглаживания — как произведение коэффициентов сглаживания звеньев: ёмкостного и Г-образного индуктивно-ёмкостного.
Наилучшими фильтрующими свойствами обладают LC-фильтры Чебышева. Напишем формулу, исходя из рекомендаций, изложенных на странице ссылка на страницу:
С1 = С2 ; С1(МкФ)/L1(мГн) = 1176/Rн 2 (Ом) .
Уменьшить напряжение пульсаций на выходе однозвенного П-образного LC-фильтра можно, включив параллельно дросселю L1 неполярный конденсатор С3 (Рис. 1г), который вместе с индуктивностью катушки образует режекторный фильтр. Если ёмкость конденсатора С3 выбрать такой, чтобы резонансная частота контура L1-С3 равнялась частоте пульсаций (F при однополупериодном выпрямлении или 2F при двухполупериодном), то большая часть напряжения пульсаций задержится этим контуром и лишь незначительная перейдёт в нагрузку.
1г), который вместе с индуктивностью катушки образует режекторный фильтр. Если ёмкость конденсатора С3 выбрать такой, чтобы резонансная частота контура L1-С3 равнялась частоте пульсаций (F при однополупериодном выпрямлении или 2F при двухполупериодном), то большая часть напряжения пульсаций задержится этим контуром и лишь незначительная перейдёт в нагрузку.
Итак: С3 = 1/(39,44×L1×F 2 ) для однополупериодных выпрямителей и
С3 = 1/(9,86×L1×F 2 ) — для двухполупериодных.
Все остальные номиналы элементов — такие же, как в предыдущей схеме.
Давайте сдобрим пройденный материал онлайн таблицей.
КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ СЛАЖИВАЮЩЕГО ФИЛЬТРА БЛОКА ПИТАНИЯ.
Транзисторные фильтры по сравнению с ёмкостными сглаживающими фильтрами имеют меньшие габариты, массу и более высокий коэффициент сглаживания пульсаций.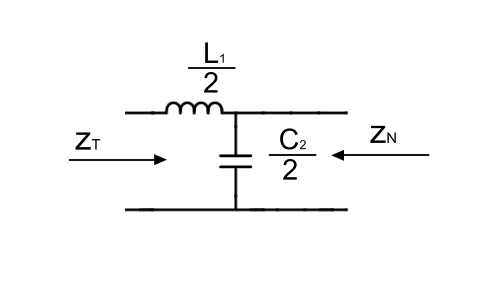
Рис.2
На Рис.2а представлена схема наиболее распространённого транзисторного фильтра.
Напряжение с высокой амплитудой пульсаций, поступающее на коллектор транзистора, по сути, является напряжением питания эмиттерного повторителя, образованного Т1.
В это же самое время цепь базы питается через резисторы смещения и интегрирующую цепь R1C1, которая сглаживает пульсации напряжения на базе. Чем больше постоянная времени T=R1C1, тем меньше пульсации напряжения на базе, а так как устройство представляет собой эмиттерный повторитель, то на выходе фильтра пульсации будут столь же малыми, как и на базе.
Для того, чтобы снизить зависимость напряжения на выходе фильтра от уровня передаваемой мощности, ток через делитель R1R2 выбирают в 5…10 раз большим, чем ток, ответвляющийся в базу при минимальном сопротивлении нагрузки.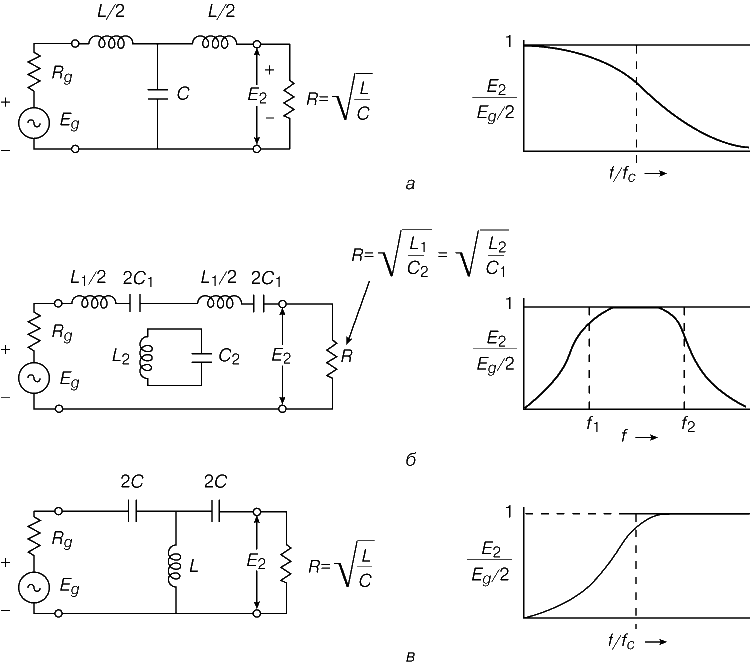
При расчёте номиналов элементов делителя, следует исходить из напряжения на базе транзистора:
Uб = Uвх — Uвх пульсаций — (2,5. 3В) .
В этом случае будет обеспечена работа регулирующего транзистора в активном режиме, а падение напряжения на нём составит величину:
Uкэ = Uвх пульсаций + (3,1. 3,6В) .
Коэффициент полезного действия транзисторного фильтра будет тем больше, чем меньше падание постоянного напряжения на силовом транзисторе. Из формулы видно, что для обеспечения высокого КПД активного сглаживающего фильтра, на вход устройства следует подавать уже отфильтрованное до определённого уровня напряжение.
На практике это делается включением на вход простейшего ёмкостного фильтра (Рис.1а), уровень пульсаций которого можно посчитать на приведённом выше калькуляторе.
Эффективность активных сглаживающих фильтров напрямую зависит от величины коэффициента усиления транзистора.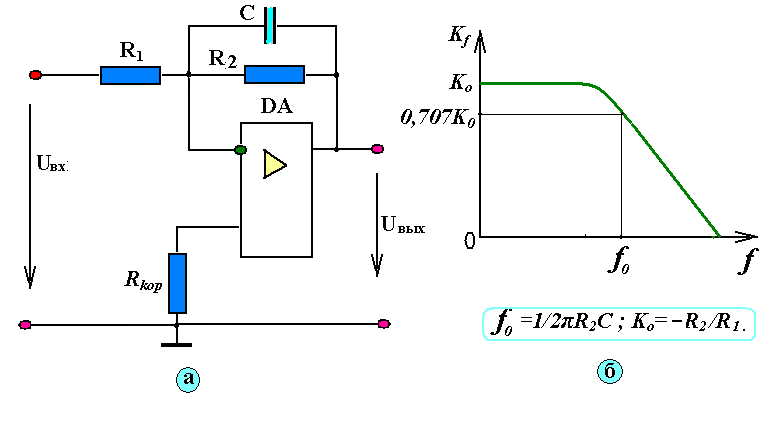 Чем выше h31 полупроводника, тем больших величин можно выбрать номиналы резисторов R1, R2 — тем лучшими фильтрующими свойствами будет обладать схема. Поэтому в данной ситуации не стоит даже рассматривать транзисторы с h31<50. Но при этом и составные транзисторы, обладающие высоким усилением — также не являются оптимальным выбором в силу повышенных падений напряжений на p-n переходах, значительно снижающих КПД транзисторных устройств.
Чем выше h31 полупроводника, тем больших величин можно выбрать номиналы резисторов R1, R2 — тем лучшими фильтрующими свойствами будет обладать схема. Поэтому в данной ситуации не стоит даже рассматривать транзисторы с h31<50. Но при этом и составные транзисторы, обладающие высоким усилением — также не являются оптимальным выбором в силу повышенных падений напряжений на p-n переходах, значительно снижающих КПД транзисторных устройств.
Для дальнейшего улучшения фильтрующих свойств сглаживающего фильтра можно применить двухзвенный RC-фильтр в цепи базы транзистора (Рис.2б).
Здесь сумма значений сопротивления резисторов R1 и R2 равна сопротивлению резистора R1 в предыдущем устройстве, а сопротивление резистора R3 равно сопротивлению резистора R2 в фильтре (Рис.2а).
Ещё эффективней будет работать транзисторный фильтр, у которого в цепь базы транзистора вместо R2 (Рис.1а), либо R3 (Рис.1б) включить стабилитрон с напряжением пробоя, равным значению, рассчитанному для резистивного делителя.
Меры по защите контактов реле от повреждения дуговыми разрядами
В процессе эксплуатации сигнализаторов уровня имеющих дискретный (релейный, транзисторный) выход, зачастую подключают индуктивную нагрузку (устройства, имеющие в своём составе катушку индуктивности). Возникновение дуговых разрядов при размыкании таких электрических цепей крайне негативно сказывается на работоспособности контактов реле и выходных каскадов датчиков, уменьшая их срок эксплуатации.
В целях устранения пагубного влияния дуговых разрядов применяются искрогасящие цепи, устанавливаемые параллельно контактам реле или параллельно нагрузке.
Не вдаваясь в физику переходных процессов и причин возникновения дуговых разрядов рассмотрим наиболее действенные и широко применяемые искрогасящие цепи постоянного и переменного тока.
Цепи постоянного тока:
Кремниевый диод включается параллельно индуктивной нагрузке, при замыкании контактов и в установившемся режиме не оказывает никакого воздействия на работу схемы.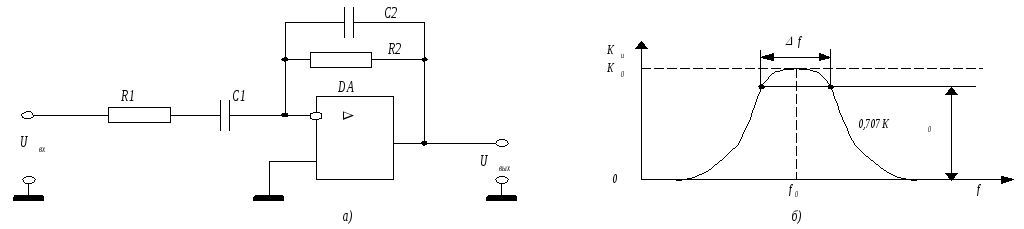 При отключении нагрузки возникает напряжение самоиндукции, обратное по полярности рабочему напряжению, диод открывается и шунтирует индуктивную нагрузку. Диоды исключительно эффективно устраняют дуговые разряды и предохраняют контакты реле от обгорания лучше, чем любые другие схемы искрогашения. Такой способ применим и к сигнализаторам с транзисторным выходом.
При отключении нагрузки возникает напряжение самоиндукции, обратное по полярности рабочему напряжению, диод открывается и шунтирует индуктивную нагрузку. Диоды исключительно эффективно устраняют дуговые разряды и предохраняют контакты реле от обгорания лучше, чем любые другие схемы искрогашения. Такой способ применим и к сигнализаторам с транзисторным выходом.
Правила выбора обратного диода:
RC-цепь является наиболее дешёвым и широко применяемым средством защиты цепей как переменного, так и постоянного тока.
В отличие от диодных схем RC-цепи можно устанавливать, как параллельно нагрузке, так и параллельно контактам реле. В некоторых случаях нагрузка физически недоступна для монтажа на ней искрогасящих элементов, и тогда единственным способом защиты контактов остается шунтирование контактов RC-цепями.
Расчет RC-цепи, подключаемой параллельно контактам реле:
где С — ёмкость RC-цепи, мкф.
I — рабочий ток нагрузки, А.
где R — сопротивление RC-цепи, Ом.
E0 — напряжение на нагрузке, В.
I — рабочий ток нагрузки, А.
Проще всего пользоваться универсальной номограммой. По известным значениям напряжения источника питания U и тока нагрузки I находят две точки на номограмме, после чего между точками проводится прямая линия, показывающая искомое значение сопротивления R. Значение емкости С отсчитывается по шкале рядом со шкалой тока I. Номограмма дает разработчику достаточно точные данные, при практической реализации схемы необходимо будет подобрать ближайшие стандартные значения для резистора и конденсатора RC-цепи.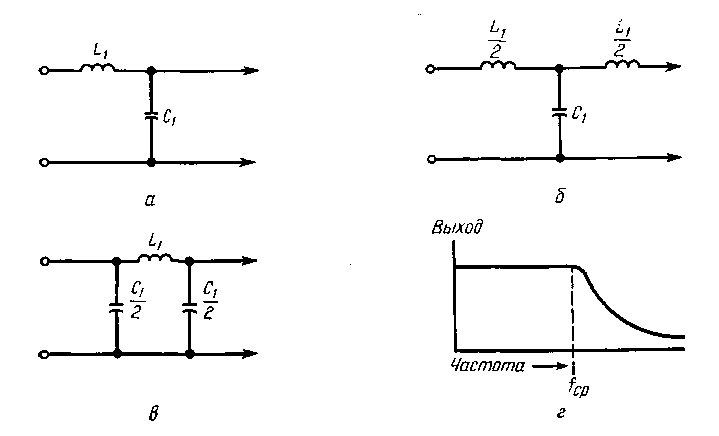
RC-цепь, подключаемая параллельно нагрузке
Применяется там, где нежелательна или невозможна установка RC-цепи параллельно контактам реле. Для расчета предлагаются следующие ориентировочные значения элементов:
Для защиты выходных транзисторных каскадов сигнализаторов RC-цепь подключают параллельно нагрузке.
Калькулятор фильтра нижних частот– ElectronicBase
Фильтр нижних частот пропускает только сигналы ниже своей частоты среза и ослабляет компоненты над ней. Вот как рассчитать различные варианты пассивных фильтров нижних частот.
В дополнение к формулам, вам могут помочь несколько калькуляторов низких частот.
Общие сведения о фильтре нижних частот
Низкий проход обозначает компонент в электротехнике, который ослабляет или блокирует высокие частоты и позволяет низким частотам проходить практически беспрепятственно.Также широко используется термин фильтр нижних частот. Термин пассивный просто означает, что схема фильтра нижних частот построена без усилительного элемента. При использовании операционного усилителя имеем активный НЧ.
Фильтр нижних частот используется, когда нежелательны быстрые и резкие изменения напряжения на выходе. Он используется, например, в конструкции низкочастотных динамиков для улучшения их акустики. Также в сетевых фильтрах часто используется фильтр нижних частот для удаления передаваемых паразитных частот из электросети.
Специалисты различают ФНЧ 1-го порядка и ФНЧ 2-го порядка. Мы объясняем элементы каждого прохода низких частот, как они работают и как рассчитать фильтр низких частот. Поскольку это очень сложные вычисления, мы также предлагаем калькулятор фильтра нижних частот .
Поскольку это очень сложные вычисления, мы также предлагаем калькулятор фильтра нижних частот .
Пассивный ФНЧ 1-го порядка
Фильтр нижних частот первого порядка состоит из последовательно соединенных резистора и конденсатора . Следовательно, термин RC lowpass является общим, где \ (R \) обозначает резистор, а \ (C \) обозначает конденсатор.Параллельно конденсатору снимается выходное напряжение \ (V_ {out} \). Это важно, потому что в противном случае это фильтр высоких частот.
В случае резких изменений входного напряжения \ (V_ {in} \) практически не падает напряжение на конденсаторе, в результате чего выходное напряжение \ (V_ {out} \) также приближается к нулю. С другой стороны, если есть медленное изменение напряжения \ (V_ {in} \), часть напряжения на конденсаторе падает. Выходное напряжение \ (V_ {out} \) изменяется с задержкой по времени.В следующем разделе мы хотим рассчитать RC-фильтр нижних частот и пролить свет на передаточную функцию фильтра нижних частот первого порядка.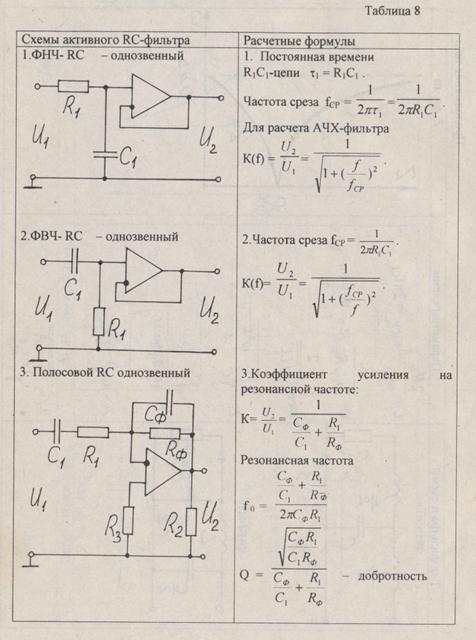
RC low pass – как это работает
Выходное напряжение \ (V_ {out} \) следует за нестабильным входным напряжением \ (V_ {in} \), задержанным во времени на той же высоте скачка. Это связано с тем, что измененное входное напряжение на короткое время проходит через конденсатор, потому что сначала нарастает емкостное сопротивление конденсатора. Когда емкостное реактивное сопротивление достигает нового значения, выходное напряжение больше не изменяется.2}} $$
Здесь \ (V_ {in} \) обозначает входное напряжение, а \ (V_ {out} \) – выходное напряжение. \ (\ Omega \) – это угловая частота, то есть произведение \ (2 \ cdot \ pi \ cdot f \) (частота). \ (C \) – это емкость конденсатора, а \ (R \) – омическое сопротивление.
Рассчитать частоту среза фильтра низких частот
Омическое сопротивление \ (R \) остается неизменным, в то время как емкостное реактивное сопротивление \ (X_C \) изменяется в зависимости от частоты. Частота среза обозначает частоту, на которой два значения равны, то есть \ (R = X_C \).Таким образом, на частоте выше частоты среза \ (X_C \) меньше, чем \ (R \), на более низкой частоте \ (X_C \) больше, чем \ (R \). При работе с частотой среза 70,71% входного напряжения выводится из-за пик-фактора \ (\ sqrt {2} \).
Расчет частоты среза для RC-фильтра нижних частот выполняется по следующей формуле:
$$ f_c = \ frac {1} {2 \ pi R C} $$
Калькулятор низких частот RC
С помощью онлайн-калькулятора вы можете рассчитать необходимые компоненты для желаемой частоты среза.
Калькулятор фильтра нижних частот RC
Начните расчет
Альтернатива: RL low pass
Если вместо конденсатора используется катушка, можно также построить фильтр нижних частот первого порядка. Однако для этого выходное напряжение должно быть отведено параллельно резистору. Принцип работы прямо противоположный: чем выше частота, тем большая часть напряжения падает на катушке.
Формула для расчета выходного напряжения выглядит следующим образом:
$$ \ frac {V_ {out}} {V_ {in}} = \ frac {1} {\ sqrt {1+ (\ omega \ frac {L} {R}) ^ 2}} $$
Частота среза рассчитывается по следующей формуле для нижних частот LR:
$$ f_c = \ frac {R} {2 \ pi L} $$
Калькулятор низких частот RL
Онлайн-калькулятор помогает рассчитать необходимые элементы конструкции для соответствующей частоты среза.
Калькулятор фильтра низких частот RL
Начните расчет
Пассивный фильтр нижних частот 2-го порядка
Низкочастотный фильтр второго порядка также состоит из двух компонентов. В фильтре нижних частот 2-го порядка катушка последовательно соединена с конденсатором, поэтому этот фильтр нижних частот также называется LC-фильтром нижних частот . Опять же, выходное напряжение \ (V_ {out} \) отводится параллельно конденсатору. Таким образом, структура идентична низкочастотному фильтру 1-го порядка, это только омическое сопротивление, замененное на катушку.
Низкочастотный проход 2-го порядка в основном выполняет ту же функцию, что и его аналог 1-го порядка, но имеет вдвое больший наклон. Таким образом, низкие частоты могут возникать, в то время как высокие частоты фильтруются вдвое эффективнее. Разница вызвана катушкой. Как индуктивная нагрузка, она намного быстрее реагирует на изменения напряжения, чем омическое сопротивление.
LC low pass – как это работает
Функция конденсатора точно такая же, как и в ФНЧ 1-го порядка. Он расположен точно в том же месте, и выходное напряжение отводится идентично.Также сопоставима реакция на единичное случайное изменение входного напряжения. Катушка имеет сопротивление, близкое к нулю, пока подается постоянное напряжение.
Разница становится очевидной только при подаче изменяющегося напряжения. Катушка более чувствительна к увеличению частоты, чем омическое сопротивление. С увеличением частоты индуктивное сопротивление катушки \ (X_L \) увеличивается, а емкость \ (X_C \) конденсатора уменьшается. Таким образом, изменение частоты на входе еще более четко отражается на уровне выходного напряжения.2 LC} $$
В расчет \ (L \) добавляется индуктивность катушки. Омическое сопротивление \ (R \) не имеет значения. Мы предоставили калькулятор нижних частот LC , чтобы упростить расчет нижних частот.
Рассчитать частоту среза на нижнем проходе LC
Индуктивное сопротивление \ (X_L \) увеличивается с частотой, а емкостное реактивное сопротивление \ (X_C \) обратно пропорционально ему – оно уменьшается с увеличением частоты. Частота среза – это частота, при которой \ (X_C = X_L \).Таким образом, на частоте, большей, чем частота среза, \ (X_C \) меньше, чем \ (X_L \). На более низкой частоте \ (X_C \) больше, чем \ (X_L \).
Частота среза для низкочастотного фильтра LC рассчитывается по следующей формуле:
$$ f_c = \ frac {1} {2 \ pi \ sqrt {LC}} $$
Калькулятор низких частот LC
Здесь вы можете рассчитать желаемую частоту среза, а также необходимые компоненты.
Калькулятор фильтра низких частот LC
Начните расчет
Калькулятор RC-фильтров – Как работают RC-фильтры
Этот сайт объясняет точную работу фильтра RC и его отдельных компонентов.Ниже мы упомянем некоторые возможности RC-цепи и типовые приложения. Затем мы объясняем, как можно рассчитать RC-фильтр, а также предоставляем калькулятор RC-цепи для наиболее распространенных вариантов RC-цепи.
RC-фильтр или RC-фильтрующий элемент в электротехнике относится к цепи с сопротивлением R и емкостью C. Эти два компонента могут быть соединены либо параллельно, либо последовательно. Возможна комбинация нескольких резисторов и конденсаторов.
Благодаря свойствам компонентов достигается соотношение между частотой на входе и напряжением на выходе . Этот эффект можно эффективно использовать в электронных схемах, которые работают по-разному в зависимости от частоты. Поэтому здесь применяются только напряжения определенной частоты.
Как работают компоненты
Сопротивление провода игнорируется в большинстве расчетов из-за его минимального размера. Омическое сопротивление R всегда остается постоянным.Он не меняет своего значения при разнице в напряжении и токе. Изменение частоты также не влияет на р.
.Конденсатор C , однако, работает как батарея с очень небольшой емкостью. Под напряжением постоянного тока он будет заряжаться и представлять собой разрыв цепи при полной зарядке. Однако, если он подключен к переменному напряжению, он образует емкостное реактивное сопротивление \ (X_C \), которое изменяется в зависимости от напряжения. Этот эффект возникает из-за того, что конденсатор постоянно заряжается и разряжается при смене полюсов.Чем ниже частота, тем длиннее циклы заряда и больше емкостное реактивное сопротивление \ (X_C \).
Сопротивление, емкость и постоянная времени RC-фильтра
При расчете RC-фильтра наиболее важными являются сопротивление и емкость. Взаимодействие этих двух элементов приводит к желаемому эффекту фильтрации. В зависимости от соединения формулы меняются для расчета, но эти две переменные всегда играют роль.
Функция конденсатора также делает важной постоянную времени RC-фильтра.Он рассчитывается на основе сопротивления и емкости и указывает необходимое время зарядки. В зависимости от схемы RC-фильтр может быть рассчитан по разным формулам, но постоянная времени RC-фильтра рассчитывается одинаково для каждого из них.
Онлайн RC калькуляторы
С помощью наших калькуляторов RC-фильтров работать со схемами проще. Из-за различных подключений резистора и конденсатора могут быть реализованы различные фильтры. Это зависит от того, подключены ли компоненты последовательно или параллельно и в какой точке снимается выходное напряжение.Часто используемые параметры – это верхний проход, нижний проход, полосовой пропуск и полосовой ограничитель, которые мы хотим рассчитать как RC-цепь.
Высокий проход
RC-фильтр верхних частот создается последовательным соединением двух компонентов, в результате чего выходное напряжение снимается выше омического сопротивления. Простой фильтр высоких частот RC – это фильтр высоких частот 1-го порядка. Сопротивление конденсатора увеличивается с уменьшением частоты и наоборот. Здесь очень пригодится калькулятор частоты среза RC-фильтра.Чем меньше сопротивление конденсатора, тем больше падение напряжения на омическом сопротивлении. Следовательно, выходное напряжение увеличивается вместе с частотой на входе. В соответствующем разделе объясняется, как рассчитать RC-фильтрующий элемент.
→ Калькулятор высоких частот RC
Проход низких
Структура RC-фильтра нижних частот и RC-фильтра верхних частот идентична, но здесь происходит отвод выходного напряжения на конденсаторе. Это дает нам прямо противоположный эффект.Сопротивление конденсатора увеличивается с уменьшением частоты. Чем больше сопротивление, тем больше падение напряжения и выходное напряжение. RC-фильтр низких частот также является фильтром низких частот 1-го порядка. В сопроводительном разделе объясняется, как рассчитать RC-цепь.
→ Калькулятор низких частот RC
Полоса пропускания
Полоса пропускания RC создается комбинацией двух RC-фильтров. Последовательная цепь RC и параллельная цепь RC соединены последовательно. Выходное напряжение снимается через параллельное соединение.Эта схема обеспечивает максимальное выходное напряжение в полосе частот. Середина этой полосы называется центральной частотой. При большей или меньшей частоте выходное напряжение падает. Наш калькулятор позволяет легко рассчитать RC-фильтр.
→ Калькулятор полосы пропускания RC
Упор ленты
Ограничитель полосы RC является аналогом полосы пропускания и построен точно так же. Область, через которую проходит полоса пропускания, ослабляется или блокируется во время полосы пропускания. Для этого просто снимается выходное напряжение в последовательной цепи.Здесь центральная частота – это центр заблокированной области. С помощью нашего калькулятора RC-частоты проще определить полосовой заградительный фильтр как RC-элемент.
→ Калькулятор упора диапазона RC
Области применения RC-фильтра
Фильтрация частот используется в динамиках для улучшения качества звука. Колонки могут воспроизводить сигналы только в правильном частотном диапазоне. Звуки на других частотах будут искажены; слышен скрип или царапанье. Таким образом, твитер имеет верхний проход, а низкочастотный динамик – нижний.Таким образом, средний диапазон использует полосу пропускания.
Все радиосигналы работают на определенной частоте, которая обычно находится в диапазоне многих мегагерц. Например, для мобильных станций частоты продаются поставщикам, чтобы обеспечить бесперебойную работу. Сигнал может передаваться только в том случае, если передатчик и приемник работают на одной частоте. Чтобы минимизировать помехи, нежелательные частоты перед передачей отфильтровываются. Для больших передатчиков фильтрация передаваемых сигналов требуется по закону.
Приемник сигнала также должен быть снабжен фильтром, чтобы нежелательные сигналы из других частотных диапазонов не принимались. Они могут быть заметны в шуме или даже мешать принимаемому сигналу. Например, при приеме сигнала определенной частоты можно достаточно точно настроить полосовой фильтр и, таким образом, исключить помехи. Типичный пример – поиск радиостанций.
Фильтрующие элементы часто используются в сетевых устройствах. В большинстве случаев они удаляют высокочастотные сигналы, которые случайно попадают в линию электропередачи и передаются.Хотя сигналы не влияют на передачу сетевого напряжения, они могут вызывать помехи в других устройствах. В этом частном случае говорят о сетевых фильтрах.
RC фильтр нижних частот
После нескольких долгих портативных сессий с шумными полосами и богатым боковым тоном с гармониками я решил попробовать звуковой фильтр нижних частот, чтобы уменьшить утомляемость ушей. Желая сделать что-то простое и быстрое, я обратился к конструкции резистора / конденсатора, они настолько просты, что мне пришлось попробовать.У этих маленьких фильтров есть место в радиолюбительстве и может прекрасно жить между установкой и наушники. На то, что выше, понадобилось всего несколько минут, чтобы склеить его Манхэттен стиль. Припой и клей отлично подходят для быстрого прототипирования. Затем он ушел в переносную коробку на следующий раз. Я мог бы использовать FB Hi-Per-Mite от NMS Dave Cripe, но у меня есть другое применение, которое стоит на заднем плане.Расчеты просты, но есть онлайн-калькуляторы, которые упрощают играть в игры “что, если” и точно настраивать значения компонентов в зависимости от угла (обрезанная) частота, несколько ссылок размещены ниже.Также легко создать таблицу, если вам это нравится. Загрузка эффектов и множественный порядок дизайны также могут быть включены в электронную таблицу.
Я решил использовать 1000 циклов в качестве частоты среза в моем. Это достаточно высоко, чтобы пропускать сигналы на частоте около 600-700 Гц без ослабления, но достаточно низко, чтобы обеспечить адекватное ослабление высоких звуковых частот, то есть шум / шипение / хэш. Еще одна мысль заключалась в том, чтобы ограничить затухание последовательными резисторами.Я не думаю, что это серьезная проблема, но я интуитивно хотел маленький резистор значения последовательно с наушниками, поэтому я выбрал 4,7 Ом (потому что они у меня были). При использовании с 32 мкФ конденсатор это дает частоту среза 1058 Гц. Я построил дизайн 2-го порядка на случай, если мне нужна была эффективность двух этапов. Заметьте, я провел параллель (иззать слово?) 10 мкФ и 22 мкФ, чтобы получить 32 мкФ. Они были в ящике для мусора, используйте вачка. Расчетная частота среза для обоих этапов вычисляется так же, как для одиночной стадии, но эффект нагрузки второй стадии перемещает фактическое срезание частоты.В этом случае до 700 циклов, поэтому при серьезном проектировании следует учитывать эффект нагрузки. В первой ссылке обсуждается этот эффект, но я не пытался учесть это, просто каскадируя два идентичных этапа, чтобы увидеть, как это будет работать.
Доказательство – производительность, и эта маленькая схема работает довольно хорошо. Он “смягчился” полосового шума и бокового тона совсем немного. Закоротка секций перемычкой выявили эффективность каждого этапа и всего фильтра.Важно: поскольку BFO на установке, которую я использую, был настроен для размещения принимаемых сигналов. на ~ 600 Гц, когда они сосредоточены в полосе пропускания, в эфире сигналы не были ослаблены, и различие в их громкости невозможно. слышно при выдергивании всего фильтра. Я не пытался измерить этот маленький фильтр ослабление полосы пропускания, ощущение, что ухо достаточно чувствительно для этого приложения.
Если вы хотите повысить комфорт работы, подарите один из этих простые маленькие аксессуары попробовать.Улучшение качества звука может стоить вам небольших усилий. Вы можете считать это промежуточным шагом на пути к Hi-Per-Mite.
Ссылки на калькуляторы и обучающие программы:
VE3WWG Calculator Очень хорошая страница с простым в использовании калькулятором и графиками Боде.
Учебное пособие по фильтрам Electronics-Tutorials. Отличное руководство, включает вычисления 2-го порядка и ссылки на другие их руководства. Всем хорошего.
Okawa Electric Design RC Low-pass Filter Design Tool Хороший калькулятор со ссылками на другие руководства.
Sengpiel audio Хороший калькулятор на аудио-сайте для немного иной точки зрения.
Вернуться на страницу антенны и ответвителя Вернуться на ГЛАВНУЮ СТРАНИЦУ
Резистор-конденсаторный калькулятор (RC) • Расчет радиочастот и электронных средств • Обмен данными в Интернете
Постоянная времени определяется как
, где τ – постоянная времени в секундах, R – сопротивление в омах и C, – емкость в фарадах.Постоянная времени RC-цепи определяется как время, за которое конденсатор достигает 63,2% своей максимальной зарядной емкости при отсутствии начального заряда. Обратите внимание, что конденсатор будет заряжен на 63,2% после τ и почти полностью заряжен (99,3%) примерно через 5 τ .
Энергия, накопленная E в конденсаторе, когда он полностью заряжен до напряжения U (время зарядки T >> τ )
, где C – емкость в фарадах, а V – напряжение в вольтах.
Максимальный ток I определяется по закону Ома:
Максимальный заряд Q определяется следующим образом:
, где C – емкость в фарадах, а U – напряжение в вольтах.
Фильтр электролитических конденсаторов на материнской плате компьютера
Приложения
Основной частью разветвителя ADSL является фильтр нижних частот.
Конденсаторы часто используются в различных электронных и электрических устройствах и системах.Вы, наверное, не найдете электронное устройство без хотя бы одного конденсатора. Конденсаторы используются для накопления энергии, обеспечения импульсной мощности, для согласования мощности, для коррекции коэффициента мощности, для связи по переменному току и блокировки постоянного тока, в электронных частотных фильтрах, в шумовых фильтрах, для запуска двигателя, для хранения информации, в настроенных схемах, в различных сенсорные устройства, емкостные сенсорные экраны мобильных телефонов и для многих других целей.
Резисторно-конденсаторные (RC) цепи можно использовать как простые фильтры нижних и верхних частот, интеграторы и дифференциаторы.
RC-фильтры нижних частот
Пример двухкаскадного RC-фильтра нижних частот второго порядка с неинвертирующим единичным усилителем, который используется в качестве буфера между двумя каскадами фильтра.
Фильтры нижних частот пропускают только низкочастотные сигналы и ослабляют высокочастотные сигналы. Частота среза определяется компонентами схемы фильтра.
Такие фильтры широко используются в электронике. Один из примеров – их использование в сабвуферах для блокировки высоких частот, которые они не могут воспроизвести.Они также используются в радиопередатчиках для блокировки нежелательных гармонических излучений. Те, кто использует подключение к Интернету ADSL, устанавливают эти фильтры в разветвители DSL, которые предотвращают помехи между телефонами и оборудованием DSL, подключенным к телефонной линии.
Фильтры нижних частот используются для преобразования сигналов перед аналого-цифровым преобразованием и называются фильтрами сглаживания. Они необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста, чтобы удовлетворить теорему о дискретизации.
Простой фильтр нижних частот показан на рисунке выше. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот. Более сложные пассивные фильтры нижних частот также используют индукторы.
В отличие от пассивных фильтров нижних частот, в активных фильтрах используются некоторые устройства усиления, например, транзисторы или операционные усилители. Пассивные фильтры также часто сопровождаются усилителями. В зависимости от количества конденсаторов и катушек индуктивности, которые влияют на крутизну частотной характеристики фильтра, их часто называют «первого порядка», «второго порядка» и т. Д.фильтры. Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.
Простой пассивный RC-фильтр верхних частот первого порядка
RC-фильтр верхних частот
Фильтры верхних частот пропускают только высокочастотные сигналы и ослабляют низкочастотные сигналы. Фильтры верхних частот используются, например, в кроссоверах аудио для блокировки низких частот сигналов, отправляемых на твитеры, которые обычно не способны обрабатывать сигналы большой мощности на низких частотах.
Активный фильтр верхних частот с операционным усилителем
Фильтры верхних частот часто используются для блокировки постоянного тока от схем, чувствительных к нему.Например, они очень распространены в схемах микрофонов, потому что микрофонам требуется питание постоянного тока, которое подается через микрофонный кабель. В то же время они записывают только сигналы переменного тока, такие как человеческий голос и музыку. Напряжение постоянного тока не должно появляться на выходе микрофона, и для его блокировки используется фильтр высоких частот.
Простой полосовой фильтр, состоящий из каскадного соединения фильтра нижних частот (C2, R2) и фильтра верхних частот (C1, R1)
Если фильтры верхних частот и нижних частот используются вместе, они образуют полосовой фильтр , который пропускает частоты только в определенном диапазоне и ослабляет частоты за пределами этого диапазона.Такие фильтры широко используются в беспроводных приемниках и передатчиках. В приемниках полосовые фильтры пропускают и слышат только сигналы в выбранном диапазоне частот, подавляя сигналы на нежелательных частотах. Передатчики всегда должны передавать мощность только в выделенном им диапазоне частот; поэтому в них используются полосовые фильтры, чтобы ограничить полосу пропускания выходного сигнала их полосой передачи.
Пассивный фильтр нижних частот
Это руководство посвящено пассивному фильтру нижних частот , широко используемому термину в электронике.Вы будете слышать или использовать этот «технический» термин почти каждый раз во время учебы или в своей профессиональной карьере. Давайте разберемся, в чем особенность этого технического термина.
Что это, Схема, формулы, кривая?Начнем с названия. Вы знаете, что такое пассивный ? Что такое низкий ? Что проходит и что фильтр ? Если вы понимаете значение этих четырех слов « Passive Low Pass Filter », вы поймете 50% « Passive Low Pass Filter », остальные 50%, которые мы изучим далее.
« Пассивный » – в словаре это означает разрешение или принятие того, что происходит или что делают другие, без активного ответа.
« Фильтр нижних частот » – это означает пропускание того, что составляет low , что также означает блокирование того, что high . Он действует так же, как традиционный фильтр для воды, который есть у нас дома / в офисе, который блокирует загрязнения и пропускает только чистую воду.
Фильтр нижних частот пропускает низкую частоту и блокирует верхнюю .Традиционная частота пропускания фильтра нижних частот в диапазоне от 30 до 300 кГц (низкая частота) и блокировка выше этой частоты, если используется в аудио приложении.
С фильтром нижних частот связано много вещей. Как было описано ранее, он будет отфильтровывать нежелательные элементы (сигнал) синусоидального сигнала (AC) .
В качестве пассивного средства мы обычно не применяем какой-либо внешний источник к отфильтрованному выходному сигналу, это может быть сделано с использованием пассивных компонентов, которые не требуют мощности, поэтому отфильтрованный сигнал не усиливается, амплитуда выходного сигнала не будет увеличиваться ни при каких условиях. Стоимость.
Фильтры нижних частот сделаны с использованием комбинации резистора и конденсатора (RC) для фильтрации до 100 кГц, но для остальных 100 кГц – 300 кГц используются резистор, конденсатор и индуктор (RLC).
Вот схема на этом изображении:
Это RC-фильтр. Обычно входной сигнал подается на эту комбинацию последовательного резистора резистора и неполяризованного конденсатора . Это фильтр первого порядка, поскольку в схеме есть только один реактивный компонент – конденсатор.Отфильтрованный выход будет доступен через конденсатор.
Что на самом деле происходит внутри схемы, довольно интересно.
На низких частотах реактивное сопротивление конденсатора будет очень большим, чем сопротивление резистора. Таким образом, потенциал напряжения сигнала на конденсаторе будет намного больше, чем падение напряжения на резисторе.
На более высоких частотах произойдет прямо противоположное. Сопротивление резистора становится выше, и из-за влияния реактивного сопротивления конденсатора напряжение на конденсаторе становится меньше.
Вот как выглядит кривая на выходе конденсатора: –
Частотная характеристика и частота среза
Давайте разберемся с этой кривой дальше
f c – частота среза фильтра. Сигнальная линия от 0dB / 118Hz до 100 KHz почти плоская.
Формула расчета прироста
Прирост = 20log (Vout / Vin)
Если мы введем эти значения, мы увидим результат усиления до тех пор, пока частота среза не станет почти 1.1 единица усиления или 1x усиления называется единичным усилением .
После сигнала отсечки ответ схемы постепенно уменьшается до 0 (ноль), и это уменьшение происходит со скоростью -20 дБ / декада . Если мы посчитаем уменьшение на октаву, оно будет -6 дБ. В технической терминологии он называется « roll-off ».
На низких частотах высокое реактивное сопротивление конденсатора останавливает прохождение тока через конденсатор.
Если мы применяем высокие частоты выше предела отсечки, реактивное сопротивление конденсатора уменьшается пропорционально увеличению частоты сигнала, в результате чего меньшее реактивное сопротивление на выходе будет равно 0 в результате короткого замыкания конденсатора.
Это фильтр нижних частот. Выбрав соответствующий резистор и соответствующий конденсатор, мы можем остановить частоту, ограничить сигнал, не влияя на сигнал, так как нет активной реакции.
На изображении выше есть слово Bandwidth . Это означает, к чему будет применено единичное усиление, и сигнал будет заблокирован. Таким образом, если это фильтр нижних частот 150 кГц, то ширина полосы будет 150 кГц. После этой полосы пропускания сигнал будет ослабевать и перестанет проходить через схему.
Также есть -3 дБ, это важно, на частоте среза мы получим усиление -3 дБ, где сигнал ослаблен до 70,7%, а емкостное реактивное сопротивление и сопротивление равны R = Xc.
Какова формула частоты среза?
f c = 1 / 2πRC
Итак, R – сопротивление, а C – емкость. Если мы поставим значение, мы будем знать частоту среза.
Расчет выходного напряженияДавайте посмотрим на первое изображение схемы, в которой 1 резистор и один конденсатор используются для формирования фильтра нижних частот или RC-цепи.
Когда на цепь подается сигнал постоянного тока, это сопротивление цепи, которое создает падение при протекании тока, но в случае сигнала переменного тока это сопротивление, которое также измеряется в Ом.
В RC-цепи две резистивные штуки . Один из них – сопротивление, а другой – емкостное сопротивление конденсатора. Итак, нам нужно сначала измерить емкостное реактивное сопротивление конденсатора, так как это понадобится для расчета импеданса схемы.
Первое сопротивление – емкостное сопротивление , формула: –
Xc = 1 / 2π f c
Выход формулы будет в Ом, поскольку Ом – это единица емкостного реактивного сопротивления, поскольку это противоположность означает сопротивление.
Вторая оппозиция – это сам резистор . Значение резистора также является сопротивлением.
Итак, объединив эти два противостояния, мы получим общее сопротивление , которое является импедансом в цепи RC (вход сигнала переменного тока).
Импеданс обозначается как Z.
RC-фильтр действует как схема « частотный зависимый регулируемый делитель потенциала ».
Выходное напряжение этого делителя =
Vout = Vin * (R2 / R1 + R2) R1 + R2 = R T
R1 + R2 – это полное сопротивление цепи, оно равно импедансу.
Итак, сложив это общее уравнение, мы получим
Решая приведенную выше формулу, получаем окончательную: –
Vout = Vin * (Xc / Z)
Пример с расчетом
Как мы уже знаем, что на самом деле происходит внутри схемы и как узнать значение. Выберем практические значения .
Давайте рассмотрим наиболее распространенные значения резистора и конденсатора: 4,7 кОм и 47 нФ. Мы выбрали это значение, поскольку оно широко доступно и его легче вычислить.Посмотрим, какой будет частота среза и выходное напряжение .
Частота среза будет: –
Решая это уравнение, частота отсечки составляет 720 Гц.
Давай, правда или нет…
Это схема. В соответствии с частотной характеристикой, описанной ранее, на частоте среза дБ будет -3 дБ, независимо от частот. Мы будем искать -3 дБ в выходном сигнале и смотреть, составляет ли он 720 Гц или нет.Вот АЧХ: –
Как вы можете видеть частотную характеристику (также называемую графиком Боде ), мы устанавливаем курсор на -3 дБ (красная стрелка) и получаем 720 Гц (зеленая стрелка) угол или полоса пропускания .
Если мы подадим сигнал 500 Гц, то емкостное реактивное сопротивление будет
Тогда Vout при подаче напряжения 5V Vin при 500 Гц: –
Фазовый сдвиг
Поскольку с фильтром нижних частот связан один конденсатор, и это сигнал переменного тока, фазовый угол на выходе обозначается как φ (Phi), что не совпадает по фазе -45 при -3 дБ или частоте среза.Почему?
Когда входное напряжение изменяет время заряда конденсатора, и из-за этого выходное напряжение отстает от входного сигнала или имеет синусоидальную форму.
Соотношение следующее: –
Увеличение входной частоты = увеличение запаса по фазе . Все эти двое пропорциональны друг другу.
Формула фазового сдвига
Фазовый сдвиг φ = -arctan (2πfRC)
Посмотрим фазовый сдвиг схемы
Это кривая фазового сдвига.Устанавливаем курсор на -45 (красная стрелка) и получаем результат частоты среза 720 Гц (зеленая стрелка).
Постоянная времени
Как мы уже узнали ранее о фазовом сдвиге и частотной характеристике, конденсатор получает эффект заряда и разряда от частот входного сигнала. Этот эффект зарядки и разрядки Постоянная времени обозначается как τ (тау). Это также связано с частотой среза.
Как?
τ = RC = 1 / 2π f c
Иногда нам нужно знать частоту среза, когда у нас есть значение постоянной времени, в таком случае, изменяя формулу, мы можем легко получить, что: –
f c = 1 / 2πRC Где RC = τ f c = 1 / 2πτ
Благодаря этому Постоянная времени RC-фильтр создает зубчатую волну, треугольную волну, если мы изменим входной сигнал с синусоидальной на прямоугольную.Это называется схемой интегратора .
Фильтр нижних частот второго порядка: формулы, расчеты и частотные кривые
Когда два каскада RC-каскада нижних частот первого порядка соединены каскадом, это называется фильтром второго порядка, так как имеется две RC-каскадные цепи.
Вот схема: –
Это фильтр нижних частот второго порядка. R1 C1 – это первый порядок, а R2 C2 – второй порядок. Каскадно они образуют фильтр нижних частот второго порядка.
Фильтр второго порядка играет роль крутизны 2 x -20 дБ / декада или -40 дБ (-12 дБ / октава).
Вот кривая отклика: –
Курсор, показывающий точку отсечки -3 дБ в зеленом сигнале, который находится в первом порядке (R1 C1), наклон при этом был замечен ранее -20 дБ / декада, а красный – на конечном выходе, который имеет наклон -40 дБ / Десятилетие.
Формулы: –
Усиление при f c : –
Это позволит вычислить усиление цепи нижних частот второго порядка.
Частота среза: –
На практике крутизна спада увеличивается в соответствии с каскадом добавления фильтра, точка -3 дБ и частота полосы пропускания изменяются от своего фактического расчетного значения, указанного выше, на определенную величину.
Эта определенная сумма рассчитывается по следующей формуле: –
Не так хорошо каскадировать два пассивных фильтра, поскольку динамический импеданс каждого порядка фильтров влияет на другую сеть в той же схеме.
Приложения
Фильтр нижних частот – широко используемая схема в электронике.
Вот несколько приложений: –
- Аудиоприемник и эквалайзер
- Фильтр камеры
- Осциллограф
- Система управления музыкой и частотная модуляция низких частот
- Генератор функций
- Блок питания
| Фильтры: обзор |
| Активный фильтр Калькулятор полосы пропускания с операционным усилителем, активный фильтр низких частот с операционным усилителем, активный Фильтр высоких частот с операционным усилителем |
| Аудио разработчик фильтра введите полосу пропускания, коэффициент усиления по напряжению и тип фильтра |
| Активный Фильтры с операционными усилителями Конструкция активных фильтров с операционные усилители |
| Формулы кроссовера третьего порядка Баттерворта и калькулятор |
| Формулы и калькулятор кроссовера Баттерворта 4-го порядка |
| Конструкция фильтра Баттерворта Синтез фильтра нижних и верхних частот Баттерворта |
| Баттерворт конструкция фильтра (RF) Фильтр нижних частот Баттерворта, фильтр верхних частот и полосовой фильтр |
| Синтез фильтра нижних и верхних частот Баттерворта |
| Дизайн Кристальные лестничные фильтры |
| Цифровой апплеты проектирования фильтров и руководства по DSP каждый инструмент создания фильтров представляет собой Java-апплет, обеспечивающий интерактивный метод проектирования и калькулятор частотной характеристики, который отображает амплитуду, фаза и групповая задержка |
| Электронный Схема кроссовера и схема калькулятора электронного кроссовера и калькулятор |
| Фильтры RC-фильтры, PI-фильтры, T-фильтры, OPamp, en Franais |
| ВЧ Разработчик фильтров вычисляет значения компонентов для сетевых фильтров HF |
| Более высокого порядка Аналоговые фильтры Баттерворта конструкции первого порядка (6 дБ / октава) двусторонние Кроссовер, двухполосный кроссовер второго порядка (12 дБ / октава), третьего порядка (18 дБ / октава) Двухполосный кроссовер четвертого порядка (24 дБ / октава) Двусторонний Кроссовер, схема Zobel (стабилизация импеданса), L-pad (динамик Затухание) |
| Дизайн LC-фильтра интерактивный дизайн-пакет для разработки аналога фильтры из индукторов и конденсаторов |
| Разработчик LC-фильтра позволяет пользователю создавать простые радиочастотные фильтры с индукторами и Конденсаторы, конструкция L-C фильтра нижних или верхних частот |
| Вычислитель резонансной частоты LC-контура |
| Пассивный формулы калькулятора кроссовера для расчета низких частот первого, второго и третьего порядка, высоких частот проходные и полосовые фильтры |
| четырехместный Adaptor dimpdance en Franais |
| Конструктор кривых RIAA Калькулятор RIAA |
| База данных РФ – конструкция фильтра Prototype Filter Design, LPF (фильтр низких частот), HPF (Фильтр высоких частот), BPF (полосовой фильтр), BSF (полосовой стоп-фильтр) |
| Horizontaal |
| Фильтры: темы |
| Фильтр 1-го порядка Дизайн для фильтров низких и высоких частот.Калькуляторы создают аналог значения компонентов, аналоговые и цифровые коэффициенты фильтра |
| Дизайн фильтра 2-го порядка для фильтров нижних и верхних частот, полосовых и полосовых фильтров. Аналоговый и цифровой фильтры представляют собой биквадратные фильтры. Калькуляторы создают аналоговые значения компонентов, коэффициенты аналогового и цифрового фильтра |
| 2-полосный кроссовер дизайнер |
| 3-полюсный Калькулятор характеристик полосового фильтра Баттерворта прост в разработке 3-полюсные полосовые фильтры (только компоненты L / C!) |
| Активный Разработка и определение размеров фильтра нижних частот Эта утилита написана на Javascript поможет вам быстро спроектировать и определить размер вашего активного Sallen-Key или Фильтр нижних частот с топологией множественной обратной связи |
| Активный Разработка и определение размеров фильтра верхних частот Эта утилита написана на Javascript поможет вам быстро спроектировать и определить размер вашего активного Sallen-Key или Топология с множественной обратной связью, фильтр верхних частот |
| Аудио стерео динамик Калькулятор дизайна шкафа |
| Band Pass Фильтры Полосовые фильтры, эта программа вычисляет идеальные значения компонентов для полосового фильтра при заданном уровне импеданса изображения, частоте и желаемый Q (Q = частота / полоса) |
| Базовый стерео динамик Калькулятор индуктивности кроссовера |
| Конструкция фильтра Баттерворта высокочастотный фильтр нижних частот |
| Калькулятор фильтра высоких частот Butterworth Pi LC Butterworth Pi LC High Калькулятор пропускного фильтра |
| Калькулятор фильтра низких частот Butterworth Pi LC Butterworth Pi Low Pass Калькулятор фильтров |
| Калькулятор фильтра высоких частот Butterworth Tee LC |
| Калькулятор фильтра низких частот Butterworth Tee LC |
| Емкость-частота-индуктивность калькулятор |
| Чебышевский БНФ Калькулятор Чебышевский БНФ Калькулятор |
| Чебышевский ХПФ Калькулятор Чебышева HPF Calculator |
| Калькулятор фильтра низких частот Chebyshev Pi LC |
| Калькулятор фильтра верхних частот Чебышева Пи LC Чебышев Пи LC High Pass Калькулятор фильтров |
| Chebyshev Tee LC High Pass Filter Calculator |
| Дизайн кроссовера Дизайн кроссовера.Пассивная программа проектирования кроссовера аудио от 6 дБ до 24 дБ … Трехпозиционный калькулятор ограничен диапазоном частот от 2 до 32 октав |
| Кроссовер Калькулятор деталей позволяет легко определять значения сеть кроссовера, которую вы собираетесь построить |
| HPF (Фильтр высоких частот) |
| LPF (Низкий Пропускной фильтр) Баттерворт, Чечышев |
| Максимально плоский Калькулятор HPF |
| Максимальная мощность (резонанс) в последовательных цепях RLC максимальная мощность (резонанс) в последовательных цепях RLC |
| Узкая полоса Калькулятор проходов позволяет проектировать узкополосные кроссоверные сети |
| Параллельный Конструктор режекторных фильтров |
| Пассивный Калькулятор дизайна кроссовера Калькулятор дизайна пассивного кроссовера |
| Pi Network Designer Введите сопротивление источника в Ом, введите сопротивление нагрузки в Ом, введите желаемое значение Q, Введите рабочую частоту |
| Калькулятор фильтра Баттерворта низких частот Саллена-Ки этот калькулятор вычисляет значения конденсатора для фильтра низких частот Саллен-Ки Баттерворта фильтр.Фильтр Саллена-Ки – простой активный фильтр на базе операционных усилителей. каскады, которые идеально подходят для фильтрации звуковых частот |
| Саллен-Ки Актив Баттерворт Лоу Калькулятор пропускного фильтра |
| Саллен-Ки Актив Баттерворт Калькулятор фильтра высоких частот |
| Конструктор режекторных фильтров серии Режекторный фильтр серии |
| T-сетевой тюнер апплет симулятора |
| Настроенный контурный калькулятор |
| Zobel сети калькулятор Zobel – это специальная схема, предназначенная для компенсации повышение импеданса, которое происходит на резонансной частоте динамика или около нее |
| Horizontaal |
Дома | Карта сайта | Электронная почта: support [at] karadimov.инфо Последнее обновление: 2011-01-02 | Авторские права © 2011-2013 Educypedia. http://educypedia.karadimov.info |
Что такое фильтр нижних частот? Учебное пособие по основам пассивных фильтров RC
Что такое фильтрация? Узнайте, что такое резисторно-конденсаторные (RC) фильтры нижних частот и где их можно использовать.
Эта статья знакомит с концепцией фильтрации и подробно объясняет назначение и характеристики резистивно-конденсаторных (RC) фильтров нижних частот.
Временная и частотная области
Когда вы смотрите на электрический сигнал на осциллографе, вы видите линию, которая представляет изменения напряжения во времени. В любой конкретный момент времени сигнал имеет только одно значение напряжения. То, что вы видите на осциллографе, – это представление сигнала во временной области .
Типичная осциллограмма проста и интуитивно понятна, но она также несколько ограничительна, потому что она не показывает напрямую частотную составляющую сигнала. В отличие от представления во временной области, в котором один момент времени соответствует только одному значению напряжения, представление в частотной области (также называемое спектром ) передает информацию о сигнале путем идентификации различных частотных компонентов , которые являются одновременно присутствуют .
Представления синусоиды (вверху) и прямоугольной волны (внизу) во временной области. Представления синусоиды (вверху) и прямоугольной волны (внизу) в частотной области.Что такое фильтр?
Фильтр – это схема, которая удаляет или «фильтрует» определенный диапазон частотных компонентов. Другими словами, он разделяет спектр сигнала на частотные компоненты, которые будут пропущены, и частотные составляющие, которые будут заблокированы .
Если у вас нет большого опыта в области анализа в частотной области, вы все равно можете не знать, что это за частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.
Давайте представим, что у нас есть аудиосигнал, состоящий из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоидальная волна во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц.Теперь предположим, что мы активируем генератор с частотой 500 кГц, который вносит высокочастотный шум в звуковой сигнал.
Сигнал, видимый на осциллографе, по-прежнему будет представлять собой только одну последовательность напряжений с одним значением в каждый момент времени, но сигнал будет выглядеть по-другому, потому что его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокую частота шумовых колебаний.
Однако в частотной области синусоидальная волна и шум представляют собой отдельные частотные компоненты, которые одновременно присутствуют в этом одном сигнале.Синусоидальная волна и шум занимают различных частей представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направляя сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.
Типы фильтров
Фильтры можно разделить на широкие категории, которые соответствуют общим характеристикам частотной характеристики фильтра .Если фильтр пропускает низкие частоты и блокирует высокие частоты, он называется фильтром нижних частот. Если он блокирует низкие частоты и пропускает высокие частоты, это фильтр высоких частот. Существуют также полосовые фильтры, которые пропускают только относительно узкий диапазон частот, и полосовые фильтры, которые блокируют только относительно узкий диапазон частот.
Фильтрытакже можно классифицировать по типам компонентов, которые используются для реализации схемы.В пассивных фильтрах используются резисторы, конденсаторы и катушки индуктивности; эти компоненты не обладают способностью обеспечивать усиление, и, следовательно, пассивный фильтр может только поддерживать или уменьшать амплитуду входного сигнала. С другой стороны, активный фильтр может как фильтровать сигнал, так и применять усиление, потому что он включает в себя активный компонент, такой как транзистор или операционный усилитель.
Этот активный фильтр нижних частот основан на популярной топологии Саллена – Ки.В этой статье исследуется анализ и конструкция пассивных фильтров нижних частот. Эти схемы играют важную роль в самых разных системах и приложениях.
RC-фильтр нижних частот
Чтобы создать пассивный фильтр нижних частот, нам нужно объединить резистивный элемент с реактивным элементом. Другими словами, нам нужна схема, состоящая из резистора и конденсатора или катушки индуктивности. Теоретически, топология нижних частот резистор-индуктор (RL) эквивалентна с точки зрения фильтрующей способности топологии нижних частот резистор-конденсатор (RC).Однако на практике гораздо более распространена версия резистора-конденсатора, и, следовательно, остальная часть этой статьи будет сосредоточена на RC-фильтре нижних частот.
RC-фильтр нижних частот.Как вы можете видеть на диаграмме, низкочастотный отклик RC создается путем размещения резистора последовательно с трактом прохождения сигнала и конденсатора параллельно нагрузке. На схеме нагрузка представляет собой отдельный компонент, но в реальной схеме это может быть что-то гораздо более сложное, например аналого-цифровой преобразователь, усилитель или входной каскад осциллографа, который вы используете для измерения. ответ фильтра.
Мы можем интуитивно проанализировать фильтрующее действие RC-топологии нижних частот, если мы узнаем, что резистор и конденсатор образуют частотно-зависимый делитель напряжения.
RC-фильтр нижних частот перерисован так, чтобы он выглядел как делитель напряжения.Когда частота входного сигнала низкая, сопротивление конденсатора высокое по сравнению с сопротивлением резистора; таким образом, большая часть входного напряжения падает на конденсатор (и на нагрузку, которая параллельна конденсатору).Когда входная частота высока, сопротивление конденсатора низкое по сравнению с сопротивлением резистора, что означает, что на резисторе падает большее напряжение и меньше передается на нагрузку. Таким образом, низкие частоты пропускаются, а высокие частоты блокируются.
Это качественное объяснение функциональности RC-низкочастотного диапазона является важным первым шагом, но оно не очень полезно, когда нам действительно нужно разработать схему, потому что термины «высокая частота» и «низкая частота» чрезвычайно расплывчаты.Инженерам необходимо создавать схемы, которые пропускают и блокируют определенные частоты. Например, в описанной выше аудиосистеме мы хотим сохранить сигнал 5 кГц и подавить сигнал 500 кГц. Это означает, что нам нужен фильтр, который переходит от прохода к блокировке где-то между 5 кГц и 500 кГц.
Частота среза
Диапазон частот, для которых фильтр не вызывает значительного затухания, называется полосой пропускания , а диапазон частот, для которых фильтр действительно вызывает значительное затухание, называется полосой задерживания .Аналоговые фильтры, такие как RC-фильтр нижних частот, всегда постепенно переходят от полосы пропускания к полосе задерживания. Это означает, что невозможно определить одну частоту, на которой фильтр перестает пропускать сигналы и начинает блокировать сигналы. Однако инженерам нужен способ удобного и краткого обобщения частотной характеристики фильтра, и именно здесь в игру вступает концепция частоты среза .
Когда вы посмотрите на график частотной характеристики RC-фильтра, вы заметите, что термин «частота среза» не очень точен.Изображение спектра сигнала, «разрезанного» на две половины, одна из которых сохраняется, а другая отбрасывается, неприменимо, поскольку затухание постепенно увеличивается по мере того, как частоты перемещаются от нижнего предела к верхнему пределу среза.
Частота среза RC-фильтра нижних частот – это фактически частота, на которой амплитуда входного сигнала уменьшается на 3 дБ (это значение было выбрано, потому что уменьшение амплитуды на 3 дБ соответствует снижению мощности на 50%). Таким образом, частота среза также называется –3 дБ, частота , и на самом деле это название более точное и информативное.Термин ширина полосы относится к ширине полосы пропускания фильтра, а в случае фильтра нижних частот ширина полосы равна частоте –3 дБ (как показано на диаграмме ниже).
Эта диаграмма передает общие характеристики частотной характеристики RC-фильтра нижних частот. Полоса пропускания равна частоте –3 дБ.
Как объяснено выше, поведение фильтра нижних частот RC-фильтра вызвано взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора.Чтобы определить детали частотной характеристики фильтра, нам необходимо математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C), а также мы можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (f C ) RC-фильтра нижних частот рассчитывается следующим образом:
Давайте посмотрим на простой пример дизайна. Значения конденсатора более строгие, чем значения резистора, поэтому мы начнем с обычного значения емкости (например, 10 нФ), а затем воспользуемся уравнением для определения требуемого значения сопротивления.Цель состоит в том, чтобы разработать фильтр, который сохранит форму звуковой волны 5 кГц и отклонит шумовую волну 500 кГц. Мы попробуем установить частоту среза 100 кГц, а позже в статье мы более тщательно проанализируем влияние этого фильтра на две частотные составляющие.
Таким образом, резистор 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который точно соответствует желаемой частотной характеристике.
Расчет чувствительности фильтра
Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типичного расчета делителя напряжения.Выход резистивного делителя напряжения выражается следующим образом:
В RC-фильтре используется эквивалентная структура, но вместо R 2 используется конденсатор. Сначала заменяем R 2 (в числителе) на реактивное сопротивление конденсатора (X C ). Затем нам нужно рассчитать величину полного импеданса и поместить ее в знаменатель. Таким образом, имеем
Реактивное сопротивление конденсатора указывает величину сопротивления току, но, в отличие от сопротивления, величина сопротивления зависит от частоты сигнала, проходящего через конденсатор.Таким образом, мы должны рассчитать реактивное сопротивление на конкретной частоте , и уравнение, которое мы используем для этого, выглядит следующим образом:
В приведенном выше примере конструкции R ≈ 160 Ом и C = 10 нФ. Предположим, что амплитуда V IN равна 1 В, поэтому мы можем просто исключить V IN из расчета. Сначала давайте рассчитаем амплитуду V OUT на частоте синусоиды:
Амплитуда синусоиды практически не изменилась.Это хорошо, поскольку мы стремились сохранить синусоидальную волну при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше, чем частота синусоидальной волны (5 кГц).
Теперь посмотрим, насколько успешно фильтр ослабит шумовую составляющую.
Амплитуда шума составляет всего около 20% от исходного значения.
Визуализация отклика фильтра
Самый удобный способ оценить влияние фильтра на сигнал – это изучить график частотной характеристики фильтра.Эти графики, часто называемые графиками Боде , имеют величину (в децибелах) по вертикальной оси и частоту по горизонтальной оси; горизонтальная ось обычно имеет логарифмический масштаб, так что физическое расстояние между 1 Гц и 10 Гц является таким же, как физическое расстояние между 10 Гц и 100 Гц, между 100 Гц и 1 кГц и так далее. Эта конфигурация позволяет нам быстро и точно оценить поведение фильтра в очень большом диапазоне частот.
Пример графика частотной характеристики.Каждая точка на кривой указывает величину, которую будет иметь выходной сигнал, если входной сигнал имеет амплитуду 1 В и частоту, равную соответствующему значению на горизонтальной оси. Например, когда входная частота равна 1 МГц, выходная амплитуда (при условии, что входная амплитуда 1 В) будет 0,1 В (поскольку –20 дБ соответствует уменьшению в десять раз).
Общая форма этой кривой частотной характеристики станет вам очень знакомой, если вы будете проводить больше времени со схемами фильтров.Кривая в полосе пропускания почти идеально плоская, а затем она начинает падать быстрее, когда входная частота приближается к частоте среза. В конечном итоге скорость изменения затухания, называемая спадом, стабилизируется на уровне 20 дБ / декаду, то есть величина выходного сигнала уменьшается на 20 дБ для каждого десятикратного увеличения входной частоты.
Оценка производительности фильтра нижних частот
Если мы внимательно построим график частотной характеристики фильтра, который мы разработали ранее в этой статье, мы увидим, что амплитудная характеристика на частоте 5 кГц по существу равна 0 дБ (т.е.е., почти нулевое затухание), а амплитуда отклика на 500 кГц составляет примерно –14 дБ (что соответствует усилению 0,2). Эти значения согласуются с результатами расчетов, которые мы выполнили в предыдущем разделе.
Поскольку RC-фильтры всегда имеют постепенный переход от полосы пропускания к полосе задерживания, и поскольку затухание никогда не достигает бесконечности, мы не можем разработать «идеальный» фильтр, то есть фильтр, который не влияет на синусоидальную волну и полностью устраняет шум.Вместо этого мы всегда идем на компромисс. Если мы переместим частоту среза ближе к 5 кГц, у нас будет большее ослабление шума, но также большее ослабление синусоидальной волны, которую мы хотим отправить в динамик. Если мы переместим частоту среза ближе к 500 кГц, мы получим меньшее затухание на частоте синусоидальной волны, но также меньшее затухание на частоте шума.
Фазовый сдвиг фильтра нижних частот
До сих пор мы обсуждали способ, которым фильтр изменяет амплитуду различных частотных компонентов в сигнале.Однако реактивные элементы схемы всегда вносят фазовый сдвиг в дополнение к эффектам амплитуды.
Понятие фазы относится к значению периодического сигнала в определенный момент внутри цикла. Таким образом, когда мы говорим, что схема вызывает фазовый сдвиг, мы имеем в виду, что она создает рассогласование между входным и выходным сигналами: входные и выходные сигналы больше не начинают и заканчивают свои циклы в один и тот же момент времени. Значение фазового сдвига, например 45 ° или 90 °, указывает, насколько сильно возникло рассогласование.
Каждый реактивный элемент в цепи вносит фазовый сдвиг на 90 °, но этот фазовый сдвиг не происходит сразу. Фаза выходного сигнала, как и величина выходного сигнала, постепенно изменяется с увеличением входной частоты. В RC-фильтре нижних частот у нас есть один реактивный элемент (конденсатор), и, следовательно, схема в конечном итоге внесет фазовый сдвиг на 90 °.
Как и в случае амплитудной характеристики, фазовую характеристику легче всего оценить, исследуя график, на котором горизонтальная ось указывает логарифмическую частоту.Описание ниже передает общую картину, а затем вы можете заполнить детали, изучив сюжет.
- Фазовый сдвиг изначально равен 0 °.
- Постепенно увеличивается, пока не достигнет 45 ° на частоте среза; во время этой части ответа скорость изменения увеличивается.
- После частоты среза фазовый сдвиг продолжает увеличиваться, но скорость изменения уменьшается.
- Скорость изменения становится очень маленькой, когда фазовый сдвиг асимптотически приближается к 90 °.
Фильтры нижних частот второго порядка
До сих пор мы предполагали, что RC-фильтр нижних частот состоит из одного резистора и одного конденсатора. Эта конфигурация представляет собой фильтр первого порядка .
«Порядок» пассивного фильтра определяется количеством реактивных элементов – т.е.е., конденсаторы или катушки индуктивности – которые присутствуют в цепи. Фильтр более высокого порядка имеет больше реактивных элементов, и это приводит к большему фазовому сдвигу и более крутому спаду. Эта вторая характеристика является основным мотивом для увеличения порядка фильтра.
Добавляя один реактивный элемент к фильтру – например, переходя от первого порядка ко второму или от второго порядка к третьему – мы увеличиваем максимальный спад на 20 дБ / декаду. Более крутой спад приводит к более быстрому переходу от низкого затухания к высокому, и это может привести к улучшенным характеристикам, когда сигнал не имеет широкой полосы частот, которая отделяет желаемые частотные компоненты от шумовых компонентов.
Фильтры второго порядка обычно строятся вокруг резонансного контура, состоящего из катушки индуктивности и конденсатора (эта топология называется «RLC» для обозначения резистор-индуктор-конденсатор). Однако также возможно создание RC-фильтров второго порядка. Как показано на схеме ниже, все, что нам нужно сделать, это каскадировать два RC-фильтра первого порядка.
Хотя эта топология определенно создает отклик второго порядка, она широко не используется – как мы увидим в следующем разделе, частотная характеристика часто уступает таковой активного фильтра второго порядка или RLC второго порядка. фильтр.
Частотная характеристика RC-фильтра второго порядка
Мы можем попытаться создать RC-фильтр нижних частот второго порядка, спроектировав фильтр первого порядка в соответствии с желаемой частотой среза и затем подключив два из этих каскадов первого порядка последовательно. В результате получается фильтр с аналогичной общей частотной характеристикой и максимальным спадом 40 дБ / декада вместо 20 дБ / декада.
Однако, если мы посмотрим на отклик более внимательно, мы увидим, что частота –3 дБ уменьшилась.RC-фильтр второго порядка ведет себя не так, как ожидалось, потому что два каскада не независимы – мы не можем просто соединить эти два каскада вместе и проанализировать схему как фильтр нижних частот первого порядка, за которым следует идентичный фильтр нижних частот первого порядка. фильтр.
Более того, даже если мы вставим буфер между двумя каскадами, чтобы первый RC-каскад и второй RC-каскад могли работать как независимые фильтры, затухание на исходной частоте среза будет 6 дБ вместо 3 дБ.Это происходит в точности , потому что два каскада работают независимо – первый фильтр имеет ослабление 3 дБ на частоте среза, а второй фильтр добавляет еще 3 дБ ослабления.
Основным ограничением RC-фильтра нижних частот второго порядка является то, что разработчик не может точно настроить переход от полосы пропускания к полосе задерживания путем регулировки добротности фильтра; этот параметр указывает, насколько затухает частотная характеристика.Если вы каскадируете два идентичных RC-фильтра нижних частот, общая передаточная функция соответствует ответу второго порядка, но коэффициент добротности всегда равен 0,5. Когда Q = 0,5, фильтр находится на границе чрезмерного демпфирования, и это приводит к «проседанию» частотной характеристики в переходной области. Активные фильтры второго порядка и фильтры на основе резонанса второго порядка не имеют этого ограничения; разработчик может управлять коэффициентом добротности и тем самым точно настраивать частотную характеристику в переходной области.
Сводка
- Все электрические сигналы содержат смесь желаемых частотных компонентов и нежелательных частотных компонентов. Нежелательные частотные составляющие обычно вызваны шумом и помехами, а в некоторых ситуациях они могут отрицательно повлиять на производительность системы.
- Фильтр – это схема, которая по-разному реагирует на разные части спектра сигнала. Фильтр нижних частот предназначен для пропускания низкочастотных компонентов и блокировки высокочастотных компонентов.
- Частота среза фильтра нижних частот указывает частотную область, в которой фильтр переходит от низкого затухания к значительному.
- Выходное напряжение RC-фильтра нижних частот можно рассчитать, рассматривая схему как делитель напряжения, состоящий из (частотно-независимого) сопротивления и (частотно-зависимого) реактивного сопротивления.


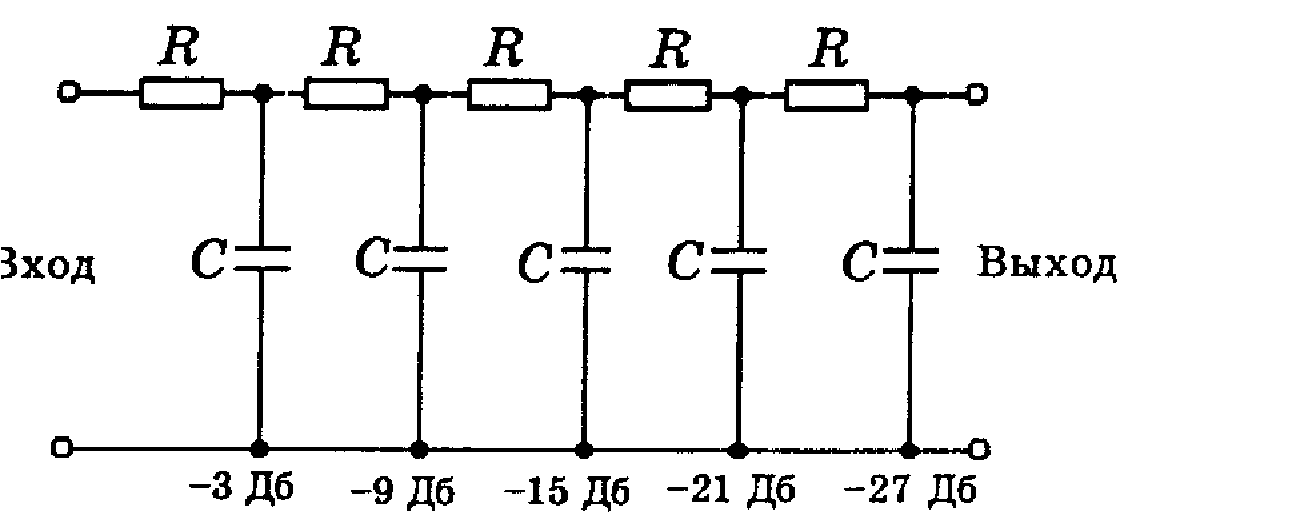 707
707