Операторный метод расчета переходных процессов (Лекция №27)
Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной , которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
Изображение заданной функции определяется в соответствии с прямым преобразованием Лапласа:
| . | (1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
или
Следует отметить, что если оригинал увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:
- При умножении оригинала на коэффициент на тот же коэффициент умножается изображение:
.
.
С использованием этих свойств и данных табл. 1, можно показать, например, что
.
Изображения производной и интеграла
В курсе математики доказывается, что если , то , где – начальное значение функции .
Таким образом, для напряжения на индуктивном элементе можно записать
или при нулевых начальных условиях
.
Отсюда операторное сопротивление катушки индуктивности
.
Аналогично для интеграла: если , то .
С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:
.
Тогда
или при нулевых начальных условиях
откуда операторное сопротивление конденсатора
.
Закон Ома в операторной форме
Пусть имеем некоторую ветвь (см. рис. 1), выделенную из некоторой
сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:
.
Тогда на основании приведенных выше соотношений получим:
.
Отсюда
| , | (2) |
где – операторное сопротивление рассматриваемого участка цепи.
Следует обратить внимание, что операторное сопротивление соответствует комплексному сопротивлению ветви в цепи синусоидального тока при замене оператора р на .
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю
.
Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
.
При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде
.
В качестве примера запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 – ; 2 – .
В первом случае в соответствии с законом Ома .
Тогда
и
Во втором случае, т.е. при , для цепи на рис. 3 следует составить операторную схему замещения, которая приведена на рис. 4. Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных токов:
откуда ; и .
Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа
,
которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:
.
На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
Например, для изображения тока в цепи на рис. 5 можно записать
.
Тогда в соответствии с данными табл. 1
,
что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение искомой переменной определяется отношением двух полиномов
,
где .
Это выражение может быть представлено в виде суммы простых дробей
| , | (3) |
где – к-й корень уравнения .
Для определения коэффициентов умножим левую и правую части соотношения (3) на ( ):
.
При
.
Рассматривая полученную неопределенность типа по правилу Лопиталя, запишем
.
Таким образом,
.
Поскольку отношение есть постоянный коэффициент, то учитывая, что , окончательно получаем
| . | (4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения равен нулю, т.е. , то уравнение (4) сводится к виду
.
В заключение раздела отметим, что для нахождения начального и конечного значений оригинала можно использовать предельные соотношения
которые также могут служить для оценки правильности полученного изображения.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные условия?
- Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты ее написания?
С использованием теоремы об активном двухполюснике записать операторное изображение для тока через катушку индуктивности в цепи на рис. 6.
- С использованием предельных соотношений и решения предыдущей задачи найти начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ: .
Ответ: .
toehelp.ru
Законы Ома и Кирхгофа в операторной форме. Пояснить принципы составления операторных схем замещения.
Пусть в цепи произошла коммутация и на её участке аb напряжение будет определяться интегро-дифференциальным уравнением
Рис. 2.2.
.
Отобразим это уравнение в операторную область, совершая над ним преобразование Лапласа
.
Тот же результат можно получить если не отображать уравнение, а составить операторную схему замещения участка цепи ab.
Рис. 2.3.
Ток в операторной схеме замещения будет найден по закону Ома для участка, содержащего эдс.
.
Закон Ома в операторной форме
, (2.10)
где Z(p)- операторное сопротивление участка цепи;
-содержит изображения источников и источники, возникающие в следствие ненулевых начальных условий.
Выделим в цепи контур, составим его операторную схему замещения и для изображений токов и напряжений запишем уравнения по первому и по второму закону Кирхгофа.
Рис. 2.4.
Законы Кирхгофа в общем виде
(2.11)
Вывод: если показать, что в операторной схеме замещения выполняются законы Кирхгофа, то следовательно её расчет может быть выполнен любым методом анализа линейных цепей (МКТ, МУП, МЭГ, метод наложения).
ОРИГИНАЛ | ИЗОБРАЖЕНИЕ | |||
| ||||
| ||||
| ||||
|
| ||||
36.продолжение
Строим график:
Особенностью расчёта цепей данного класса является то, что, на его точность окажет сильное влияние идеализация ключевого и индуктивного элементов. Если допустить мгновенность размыкания, то на индуктивности возникнет бесконечно большое напряжение, но на практике такое невозможно. При резком изменении тока индуктивности может загореться дуга в размыкателе или возникнуть высокочастотный колебательный контур, образованный индуктивностью и распределённой межвитковой ёмкостью катушки. Часть энергии при такой коммутации неизбежно превратится в теплоту электрической дуги или будет излучаться в виде электромагнитных волн. Это означает, что электрическую цепь нельзя практически рассматривать как абсолютно замкнутую систему и нельзя ожидать точного выполнения обобщенного закона коммутации. Чем ближе свойства элементов цепи к своим идеализациям, тем точнее обобщенный закон коммутации описывает процесс в цепи.
Пути восстановления оригинала функции по известному ее операторному изображению.
Под p условимся принимать комплексное число p = d + jw (можно рассматривать как комплексную частоту). Функцию времени (ток, напряжение) обозначают f(t) и называют оригиналом. Ей соответствует функция F(p) – изображение. Соответствие F(p) = f(t) устанавливается с помощью преобразований:
– прямое преобразование Лапласа:
(1)
– обратное преобразование Римана-Мелина:
(2)
Изображение напряжения на конденсаторе.
Напряжение на конденсаторе uc часто записывают в виде:
,
где не указаны пределы интегрирования по времени. Более полной является следующая запись:
,
где учтено, что к моменту времени t напряжение на конденсаторе определяется не только током, протекающим через C в интервале времени от 0 до t, но и тем напряжением uc(0), которое было на нем при t=0.
Поэтому: .
Простейшие операторные соотношения содержатся в справочном материале многих учебных пособий в виде готовых таблиц.
Отметим основные свойства преобразования Лапласа:
1) Соответствие между оригиналом и изображением взаимно однозначно: каждой функции f(t) соответствует F(p) и наоборот.
2) При умножении оригинала f(t) на постоянную величину a, умножается и изображение:
af(t) . = × aF(p) .
3) Изображение суммы функций равно сумме изображений этих функций.
Эта теорема позволяет по известному изображению функции в виде рациональной дроби:
найти соответствующий ей оригинал, где
B(p) = bmpm + bm-1pm-1 + … + b1p + b0 = bm (p–p1)(p–p2)…(p–pm) .
p1, p2, … , pm – корни уравнения B(p)=0.
Теорема разложения аналитически представляется формулой:
.
Доказательство:
.
Из курса математики известно, что если n<m, ak и bk – вещественные числа, а корни p1, p2, … , pm уравнения B(p)=0 различные, то дробь может быть представлена в виде суммы простых дробей:
.
Для определения коэффициента A1 умножим обе части уравнения на (p–p1):
.
Рассмотрим это выражение при p®p1. Правая часть дает A1, левая представляет собой неопределенность, так как множитель (p–p1) дает ноль, и знаменатель B(p) при p=p1 тоже обращается в ноль.
Раскроем неопределенность по правилу Лопиталя. С этой целью производную от числителя разделим на производную от знаменателя, и найдем предел дроби.
, где
B’(p) – производная от B(p) по p,
B’(p1) – значение B’(p) при p=p1,
A(p1) – значение A(p) при p=p1.
Следовательно, при p®p1 получаем уравнение:
. Аналогично: .
Таким образом, .
Пусть изображение какой-либо функции времени, например тока, представлено в виде дроби:
.
Перейдем от изображения к оригиналу. Оригиналом левой части является i(t). Оригинал правой части равен сумме оригиналов ее слагаемых. Так как множители – есть постоянные числа, а функциями p являются множители , которым соот-вуют функции времени вида . Поэтому: .
Последовательность вычислений по формуле такова:
1) Приравниваем B(p) к нулю и определяем корни p1, p2, … ,pn.
2) Вычисляем производную B’(p) и подставляем в нее корни p1, p2, … ,pn (поочередно).
3) Подставляем в числитель корни p1, p2, … ,pn. Определяем его значения – A(pk).
4) Вычисляя отдельные слагаемые и суммируя их, определяем оригинал f(t).
Замечания к формуле разложения:
1) Формула разложения применима при любых начальных условиях и при любых практически встречающихся формах напряжения источника эдс или тока, воздействующего на схему.
2) Если уравнение B(p)=0 имеет комплексно-сопряженные корни, то слагаемые в формуле разложения оказываются также комплексно-сопряженными и в сумме дают действительное слагаемое.
31. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения R–L-цепи к источнику синусоидального напряжения.
y-фаза коммутации
Рис. 1.6.
1. Записываем решение как сумму свободной и установившейся составляющих
.
2. Установившийся ток находим комплексным методом.
3. Находим свободную составляющую.
3.1. Определение общего вида свободной составляющей смотри в примере 1.
3.2. Определяем постоянную интегрирования.
По первому закону коммутации имеем ток в цепи при t=0+ равным 0. Тогда ,
.
4. Записываем ответ и строим график:
Рис. 1.7.
Здесь следует заметить, что интенсивность переходного процесса зависит ещё и от фазы коммутации. Для параметров, приведённых на графике имеет место близость к максимально возможному переходному процессу при фазе коммутации Y®180о. При слабом затухании с увеличением постоянной времени ( ) угол сопротивления j®90о, тогда при Y®180о будет иметь место максимальная интенсивность переходного процесса и ток дросселя может достигать ударного значения, равного удвоенной амплитуде установившейся величины.
32. Алгоритм расчета переходного процесса классическим методом в цепи второго порядка на примере подключения R–L–C-цепи к источнику постоянного напряжения.
Рассмотрим два случая:
а) ;
б) .
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
. | (1) |
Тогда для первого случая принужденная составляющая этого напряжения
. | (2) |
Характеристическое уравнение цепи
,
решая которое, получаем
.
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1. или , где – критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.
В этом случае
. | (3) |
2. – предельный случай апериодического режима.
В этом случае и
. | (4) |
3. – периодический (колебательный) характер переходного процесса.
В этом случае и
, | (5) |
где – коэффициент затухания; – угловая частота собственных колебаний; – период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
.
Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации , запишем для t=0 два уравнения:
решая которые, получим
; .
Таким образом,
.
Тогда ток в цепи
и напряжение на катушке индуктивности
.
На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .
Для критического режима на основании (2) и (4) можно записать
.
При
Таким образом
и
.
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
.
Для нахождения постоянных интегрирования запишем
откуда и .
Тогда
.
На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
и
,
где ; ; .
Таким образом,
и .
Здесь также возможны три режима:
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 – ; 2 – ; 3 – , – которые представлены на рис. 6,а…6,в соответственно.
studopedia.net
Закон Ома и законы Кирхгофа в операторной форме — Студопедия.Нет
Используя операторное представление тока, напряжения и ЭДС при переходном процессе, т.е. функции I ( p), U (p) и E(p), а также операторное сопротивление Z (p) и
проводимость Y ( p), можно получить выражения для законов Ома и Кирхгофа в
операторной форме аналогичные их символическим представлениям (3.58), (3.70) и (3.72) для цепи переменного синусоидального тока.
Закон Ома в операторной форме
Рассмотрим последовательный контур, содержащий элементы R , L и C , при ненулевых начальных условиях i L (0) ≠ 0 и u C (0) ≠ 0 , на который воздействует ЭДС
e(t )известной формы(рисунок6.17,а).
а) б)
Рисунок 6.17 – Исходная (а) и операторная (б) схемы замещения последовательного контура
На основании 2-го закона Кирхгофа для мгновенных значений тока и напряжений
6) рассматриваемой цепи можно составить следующее уравнение:
)+ u L(t )+ u C(t )= e(t )u R(t
или
Ri(t )+ L | di(t ) | + u C | (0 )+ | 1 | t i(t )dt = e(t ), | (6.122) | |
dt | C ∫ | ||||||
0 | |||||||
где u C (0 ) — начальное напряжение на конденсаторе. | |||||||
Рассматривая заданную ЭДС e(t ) | и искомый ток i(t ) | в качестве оригиналов, | |||||
положим, что им соответствуют изображения I (p) и E(p), т.е. e(t )G E( p) и i(t )G I (p).
На основании свойства линейности преобразования Лапласа и результатов, представленных в разделах 6.14.2 – 6.14.4, уравнение (6.122) можно записать в операторной форме:
158
RI ( p)− Li L(0)+ pLI ( p)+ | u C(0) | + | 1 | I ( p) | = E( p), | |||||||||||||
p |
| |||||||||||||||||
pC | ||||||||||||||||||
откуда после несложных преобразований получим уравнение | (0 ) | |||||||||||||||||
1 | u | C | ||||||||||||||||
R + pL + | I ( p)= E( p)+ Li | L | (0 )− | (6.123) | ||||||||||||||
| p | |||||||||||||||||
pC | ||||||||||||||||||
| или | Z (p)I (p)= E * (p), | |||||||||||||||||
| (6.124) | ||||||||||||||||||
| где коэффициент | 1 | |||||||||||||||||
Z ( p)= R + pL + |
| (6.125) | ||||||||||||||||
| pC | |||||||||||||||||
называется операторным сопротивлением контура, а функция | ||||||||||||||||||
E * ( p)= E( p)+ Li L(0)− | u C(0) |
| (6.126) | |||||||||||||||
| ||||||||||||||||||
p | ||||||||||||||||||
— приведенной операторной ЭДС.
Приведенная операторная ЭДС E *(p) учитывает ненулевые начальные условия в
цепи: токи в индуктивностях и напряжения на ёмкостях в момент коммутации.При
нулевых начальных условиях, когда i L(0)=0 и u C(0)=0, E *( p)= E(p), т. е.
приведенная ЭДС совпадает с изображением ЭДС источника, действующего в цепи.
Уравнению (6.123), полученному для схемы цепи, изображенной на
рисунке 6.17, а, можно поставить в соответствие схему, приведенную на рисунке 6.17, б.
Эту схему называют эквивалентной операторной схемой или схемой изображений.
Эквивалентная операторная схема может быть получена из исходной схемы цепи, если индуктивность L и ёмкость C в ней заменить операторными сопротивлениями Z L( p)= pL и Z C( p)=1 ( pC ), ток i(t ) и ЭДС e(t ) — их изображениями I ( p) и E(p), а
ненулевые начальные условия, соответствующие моменту коммутации t = 0 , учесть путем введения в схему дополнительных источников ЭДС Li L (0) и u C (0 ) p .
Источники Li L (0 ) и u C (0) p в выражении(6.126)приведенной ЭДС E *(p)
называются внутренними (или расчетными) источниками, так как обусловлены запасом энергии в магнитном поле катушки (источник Li L (0)) или в электрическом поле
конденсатора (источник u C (0 ) p ).ЭДС e(t ),а также ее изображение E( p),называются
внешними ЭДС.
Из операторного уравнения (6.124) следует, что
I ( p)= E*(( p)), I (p)= E * (p)Y (p).
Z p
Соотношения (6.127) являются законами Ома в операторной форме. Функция Y ( p),т.е. операторная проводимость,определяется равенством
Y ( p)= | 1 | = | 1 | . | (6.128) | |||||
Z ( p) | R + pL +1( pC ) | |||||||||
сопротивление Z (p), | ||||||||||
Примечание –Отметим,что | при | p = j ω | операторное | |||||||
определяемое формулой (6.125), переходит в комплексное сопротивление ветви
159
Z ( j ω)= R + j ω L − j ω1C.
При этом между операторной формой закона Ома (6.127) в переходном режиме и его символическим (комплексным) представлением (3.33) в стационарном режиме синусоидального тока сохраняется формальная аналогия.
studopedia.net
Закон Ома в операторной форме — Мегаобучалка
Рассмотрим цепь r,L,C (рис. 14-1), которая была подключена к источнику e1(t) и в момент t=0 переключается к источнику e(t)
Закон Ома для мгновенных значений после переключения запишется так:
Нижний предел интеграла, равный –(бесконечность) берется в том случае, к моменту переключения рубильника t=0 режим в цепи установился, т. е. к источнику э. д. с. e1(t) цепь была включена в момент времени t=–(бесконечность) (только при этих условиях режим к моменту переключения рубильника теоретически мог установиться).
Если к моменту переключения режим не установился, то в качестве нижнего предела нужно брать —t1, где t1 — время, прошедшее с момента включения источника e1(t) до момента t=0
Рис. 14-1.
Постановка у интеграла нижнего предела, равного –(бесконечность) или –t1 имеет целью подчеркнуть, что в момент коммутации конденсатор уже был заряжен, т. е.
(14-16)
где Uc(0) — напряжение на емкости в момент переключения, т. е. при t=0
Чтобы перейти от закона Ома, записанного для мгновенных значений (оригиналов), к его выражению в операторной форме, нужно в соответствии с формулой (14-1) поступить так: умножить обе части равенства (14-15) на e^(-pt)*dt и проинтегрировать от нуля до (бесконечность). Тогда получим:
Полагая, что
и учитывая формулы (14-4), (14-7) и (14-16), получаем следующее алгебраическое уравнение:
откуда получается закон Ома в операторной форме для цепи r,L,C.
Последнее равенство справедливо и в том случае, когда процесс переключения рубильника еще не был установившимся. В обоих случаях под i(0) и Uc(0) надо понимать ток в индуктивности и напряжение на емкости в момент переключения рубильника. Заметим,
что в соответствии со сказанным выше нужно было бы писать i(0+) и Uc(0+). Но так как ток в индуктивности и напряжение на емкости не изменяются скачком при t=0 будем писать короче: i(0) иUc(0).
Выражение, стоящее в знаменателе, назовем полным сопротивлением цепи r,L,C в операторной форме или операторным сопротивлением
(14-18)
Сопротивление в операторной форме уже встречалось в § 13-14 и теперь получено вполне строго. Напомним, что сопротивление цепи r,L,C в операторной форме построено так же, как ее комплексное сопротивление, если в последнем заменить j*(омега, как w) через p. Величина, обратная операторному сопротивлению, называется операторной проводимостью:
Операторная э. д. с. цепи, стоящая в числителе (14-17), состоит не только из операторного выражения внешней э.д.с., т.е. E(p), но и еще из двух слагаемых, которые определяются начальными условиями, т. е. током в индуктивности i(0)=iL(0) и напряжением на емкости Uc(0). Иными словами, наличие двух дополнительных ЭДС Li(0) и –Uc(0)/p которые можно назвать внутренними или расчетными э. д. с., указывает на то, что в магнитом поле катушки и вэлектрическом поле конденсатора в момент коммутации была запасена энергия. Положительные направления этих э. д. с. выбраны совпадающими с положительным направлением тока ветви.
Заметим, что, как и ранее, положительные направления тока и напряжения на конденсаторе считаются совпадающими. Если же до коммутации конденсатор был заряжен и, стало быть, положительное направление напряжения на нем до коммутации Uc- было задано, а положительное направление тока через конденсатор выбрано противоположным положительному направлению Uc- внутренняя или расчетная э. д. с., обусловленная емкостью, должна быть взята с обратным знаком, т. е. +Uc(0)/p.
Особенно просто выглядит выражение (14-17) при нулевых начальных условиях, т. е. при iL(0)=0 и Uc(0)=0:
(14-19)
Тогда оно полностью аналогично закону Ома в комплексной форме.
Вопрос16
megaobuchalka.ru
Законы Ома и Кирхгофа в операторной форме
Первый закон Кирхгофа
.
Второй закон Кирхгофа
.
Правило составления операторных уравнений по I и II законам Кирхгофа точно такое, как для действительных токов.
Для k-ой ветви, содержащей элементы , имеем:
.
Согласно (8-10), операторное уравнение при ненулевых начальных условиях имеет вид
или
.
Величину
(11)
называют обобщенным, или операторным сопротивлением ветви.
Операторная запись законов Кирхгофа
.
Закон Ома для k-й ветви
.
Следует отметить, что структура записи операторного сопротивления ветви и комплексное сопротивление той же ветви тождественны. Одно из другого можно получить заменой на , т.е. .
При нулевых начальных условиях способ расчета любых сложных цепей при переходных процессах операторным методом аналогичен способам расчета установившихся процессов комплексным методом.
При ненулевых начальных условиях II закон Кирхгофа можно записать
.
Рассматривая члены и как ЭДС добавочных источников энергии в контурах, можно использовать все общие методы расчета сложных цепей.
При расчете токов переходных процессов в сложных цепях операторным методом необходимо составить для данной цепи эквивалентную операторную схему замещения. В этом случае необходимо знать операторные схемы замещения отдельных схемных элементов (рис. 6).
Рис.6. Соответствие изображений с ненулевыми начальными условиями
во временной и операторной областях
В частности, можно воспользоваться методом наложения и рассчитать процесс в цепи сначала при нулевых начальных условиях, а затем наложить на него процесс, возникающий только под действием одних добавочных ЭДС, т.е. обусловленный первоначальным запасом энергии в цепи.
Рассмотрим, как можно преобразовать операторные схемы при последовательном и параллельном соединениях нескольких участков.
Пусть цепь состоит из одного контура:
.
Величина является операторным сопротивлением всей цепи. При последовательном соединении участков их операторные сопротивления складываются.
Рассмотрим параллельное соединение двух ветвей, в каждой из которых имеются элементы :
где .
Суммарный ток в неразветвленной части цепи
.
Очевидно, что при ненулевых начальных условиях нельзя представить как произведение на некоторый множитель , имеющий смысл операторной проводимости. Это можно записать только при нулевых начальных условиях:
.
Величина
,
называется операторной проводимостью.
3.3.Переход от изображения к оригиналу. Теорема разложения
Функции токов и напряжений, преобразованные по Лапласу могут быть представлены, как отношение полиномов
(12)
где , полиномы от , причем и коэффициенты и действительные. Изложим содержание второй теоремы разложения, позволяющей находить оригинал по изображению (12).
Если известны корни многочлена то зависимость (12) можно переписать в виде
где — кратность корня , – количество различных корней.
1. Пусть
где – различные вещественные и комплексные корни.
Тогда оригинал находят по формуле
2. Если изображение имеет вид
т.е. один характеристический корень равен нулю, то
или
Нулевой корень появляется когда в цепи имеются источники постоянной ЭДС. Выделенный постоянный член представляет собой установившийся ток или напряжение в цепи.
3. Случай кратных корней.
Пусть
где
Тогда оригинал находят по формуле
.
Коэффициенты определяются зависимостью
Пример расчета цепи
Главное достоинство операторного метода для расчета переходных процессов, заключающееся в алгебраизации дифференциальных уравнений цепи, особенно проявляется при расчете сложных цепей. Учитывая члены u как добавочные ЭДС, можно применить к расчету переходных процессов все методы расчета сложных цепей. Решим задачу, рассмотренную в пункте 2.2, операторным методом. Соответствующая схема замещения представлена на рис. 6.
Рис. 6. Схема замещения в операторной форме
Применяя к схеме замещения в операторной форме известные методы расчета цепей постоянного тока, найдем искомые токи в операторной форме. Воспользуемся методом непосредственного использования законов Кирхгофа. Имеем
Учитывая, что для данного случая , , получим
или в матричном виде
Отсюда находим
, (13)
, (14)
. (15)
Теперь можно найти оригиналы изображений (13-15). Для этого представим изображения в следующем виде:
, , .
где , , ,
. (16)
Тогда согласно второй теореме разложения имеем
где , – корни многочлена (16).
В результате получаем
,
,
.
Как видно, найденные токи полностью совпадают с токами, рассчитанными классическим методом.
4. домашнее задание
Варианты заданий
На приведены схемы электрических цепей, у которых переходные процессы вызываются замыканием (или размыканием) ключа « ». Коммутация происходит в момент времени . В цепи действует источник постоянной ЭДС . Требуется определить токи (или напряжения) двумя методами: классическим и операторным.
В соответствии с заданиями одни студенты решают задачи вариант « », другие – варианта « ». На основании полученного аналитического выражения строится график изменения искомой величины в зависимости от времени.
Вариант 1
Определить:
А. Напряжение на катушке при переходном процессе.
В. Напряжение на конденсаторе при переходном процессе.
Вариант 2
Определить:
А. Ток в конденсаторе при переходном процессе.
В. Ток в резисторе при переходном процессе.
Вариант 3
Определить:
А. Ток в конденсаторе при переходном процессе.
В. Ток в индуктивности при переходном процессе.
Вариант 4
Определить:
А. Напряжение на индуктивности при переходном процессе.
В. Ток в резисторе при переходном процессе.
Вариант 5
Определить:
А. Напряжение на индуктивности при переходном процессе.
В. Напряжение на конденсаторе при переходном процессе.
Вариант 6
Определить:
А. Ток в резисторах и при переходном процессе.
В. Ток в конденсаторе при переходном процессе.
Вариант 7
Определить:
А. Ток в резисторе при переходном процессе.
В. Ток в индуктивности при переходном процессе.
Вариант 8
Определить:
А. Ток в конденсаторе при переходном процессе.
В. Напряжение на индуктивности при переходном процессе.
Вариант 9
Определить:
А. Ток в индуктивности при переходном процессе.
В. Ток в конденсаторе при переходном процессе.
Вариант 10
Определить:
А. Ток в индуктивности при переходном процессе.
В. Напряжение на конденсаторе при переходном процессе.
Вариант 11
Определить:
А. Ток в резисторе при переходном процессе.
В. Напряжение на индуктивности при переходном процессе.
Вариант 12
Определить:
А. Напряжение на индуктивности при переходном процессе.
В. Ток в конденсаторе при переходном процессе.
Вариант 13
Определить:
А. Напряжение на конденсаторе при переходном процессе.
В. Напряжение на индуктивности при переходном процессе.
Вариант 14
Определить:
А. Ток в резисторе при переходном процессе.
В. Ток в конденсаторе при переходном процессе.
Вариант 15
Определить:
А. Ток в индуктивности при переходном процессе.
В. Напряжение на индуктивности при переходном процессе.
Вариант 16
Определить:
А. Ток в конденсаторе при переходном процессе.
В. Напряжение на индуктивности при переходном процессе.
Вариант 17
Определить:
А. Напряжение на индуктивности при переходном процессе.
B. Ток в конденсаторе при переходном процессе.
Вариант 18
Определить:
А. Ток в резисторе при переходном процессе.
В. Напряжение на индуктивности при переходном процессе.
Вариант 19
Определить:
А. Ток в резисторах и при переходном процессе.
В. Напряжение на индуктивности при переходном процессе.
Вариант 20
Определить:
А. Напряжение на индуктивности при переходном процессе.
В. Напряжение на конденсаторе при переходном процессе.
Требования к оформлению
1. Домашнее задание выполняется на листах формата 210×297 мм.
2. Прежде чем приступить к решению задачи, необходимо под заголовком “Задание” полностью переписать задание из пособия и перечертить схему.
3. Если для выполнения домашнего задания используются математические пакеты (вычисление корней полинома, решение системы уравнений и т.д.), то необходимо в местах их непосредственного использования привести соответствующие листинги программ (или их вырезки) с комментариями.
4. При построении графиков обязательно указываются величины, отложенные вдоль осей и единицы измерения.
5. Решение задачи разными методами начинается с новой страницы, с указанием соответствующего метода озаглавленной “Решение”. Вначале целесообразно построить схему и нанести на ней положительные направления токов и напряжений.
Затем составляются уравнения в общем виде. Дальнейшие расчеты рекомендуется вести не в общем виде, а подставляя конкретные числа.
6. Все расчеты целесообразно сопровождать пояснениями и проводить по пунктам в последовательности, указанной в задании.
7. В окончательных числовых результатах обязательно следует указать единицы измерения, в которых получен ответ.
8. При решении следует пользоваться обозначениями международной системы единиц СИ.
5. Контрольные вопросы
1. Дайте понятие переходного процесса в электрической цепи.
2. Сформулируйте законы коммутации.
3. В чем заключается сущность классического (операторного) метода расчета переходных процессов? Назовите их достоинства и недостатки.
4. Чем определяется порядок дифференциальных уравнений?
5. Что такое характеристическое уравнение? Что определяется из этого уравнения?
6. Что такое постоянная интегрирования? Как она определяется при расчетах переходных процессов?
7. Опишите порядок расчета переходного процесса классическим (операторным, частотным) методом.
8. Что понимают под выражениями «независимые условия начальные» и «зависимые условия начальные»?
9. Что такое свободная составляющая переходного процесса? Что такое принужденная составляющая переходного процесса?
10. Чем отличается апериодический переходный процесс от колеба-тельного в электрической цепи?
11. Объясните возникновение затухающих колебаний в электрических цепях при коммутациях с физической точки зрения.
12. Назовите правила составления комплексных (операторных) схем замещения.
13. Как можно найти изображение функции?
17. Какие способы перехода от изображения к оригиналу функции вы знаете?
18. Существует ли связь между прямым преобразованием Лапласа и прямым преобразованием Фурье?
Список литературы
1. Л.А. Бессонов Теоретические основы электротехники. Электрические цепи. Изд-во Юрайт, Серия: Бакалавр, 704 с. 2011 г.
2. Г.И. Атабеков. Теоретические основы электротехники. Линейные электрические цепи. Изд-во Лань, Серия: Учебники для вузов. Специальная литература, 592 с, 2010 г.
3. Макаров И.М., Менский Б.М. Таблица обратных преобразований Лапласа и обратных -преобразований: Дробно-рациональные изображения.: Учебное пособие для втузов. – М.: Высш. школа, 1978. – 247 с.
Содержание
1. Возникновение переходных процессов и законы коммутации 3
2. Классический метод расчета переходных процессов 6
2.1. Теоретические сведения 6
2.2. Пример расчета цепи. 9
3. Операторный метод расчета переходных процессов 14
3.1. Операторное изображение функций, их производных
и интегралов. 14
3.2. Законы Ома и Кирхгофа в операторной форме 18
3.3. Переход от изображения к оригиналу.
Теорема разложения. 21
3.4. Пример расчета цепи. 23
4. Домашнее задание 25
4.1. Варианты заданий. 25
4.2. Требования к оформлению. 33
5. Контрольные вопросы 34
Список литературы 35
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Закон Ома и законы Кирхгофа для мгновенных значений токов и напряжений. Законы Ома и Кирхгофа в символической и операторной формах.
⇐ ПредыдущаяСтр 5 из 5
Первый закон Кирхгофа. Алгебраическая сумма мгновенных токов, притекающих к узлу равна нулю.
Заметим, что первый закон Кирхгофа можно сформулировать и так: сумма мгновенных токов, притекающих к узлу, равна сумме токов, вытекающих из этого узла. В более общей форме: алгебраическая сумма токов, притекающих к произвольному сечению, равна нулю.
Пример. Записать первый закон Кирхгофа для следующего узла (рис. 1.14.2).
Решение. .
Второй закон Кирхгофа для мгновенных величин. Алгебраическая сумма мгновенных падений напряжений в контуре равна алгебраической сумме мгновенных ЭДС в этом контуре.
где n – количество пассивных элементов в контуре;
m – количество источников ЭДС в контуре.
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие.
Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:
– комплексная амплитуда тока. = Iampejφ
– комплексная амплитуда напряжения. = Uampejφ
– комплексное сопротивление. Импеданс.
φ – угол сдвига фаз между током и напряжением.
e – константа, основание натурального логарифма.
j – мнимая единица.
Iamp , Uamp – амплитудные значения синусоидального тока и напряжения.
Для последовательно соединенных элементов формула импеданса имеет следующее значение:
При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:
Z_ – импеданс последовательной цепи,
R – её активное сопротивление,
XC – ёмкостное сопротивление.
При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:
Операторная форма:
Закон Ома:
Законы Киргофа:
Операторная запись законов Кирхгофа
При ненулевых начальных условиях II закон Кирхгофа можно записать
Символическая форма:
Закон Ома:
Комплексное сопротивление:
Величина, обратная комплексному сопротивлению, – комплексная проводимость:
Законы киргофа в символической форме:
Согласно первому закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:
Подставив вместо ik в (2.63) Íkejωt и вынеся ejωt за знак суммы, получим ejωtΣÍk=0. Так как ejωt не равно нулю при любом t, то:
Уравнение (2.63,а) представляет собой первый закон Кирхгофа в символической форме записи.
Пусть замкнутый контур содержит n ветвей и каждая k- ветвь в общем случае включает в себя источник ЭДС ek, резистор Rk, индуктивную катушку Lk и конденсатор Ck, по которым протекает ток ik.
Тогда по второму закону Кирхгофа:
Но каждое слагаемое левой части можно заменить на ÍkZk, а каждое слагаемое правой части – на Ék. Поэтому уравнение примет вид:
Уравнение (2.65) представляет собой второй закон Кирхгофа в символической форме записи.
Изображение синусоидальных ЭДС, напряжений и токов с помощью вращающихся векторов и комплексных чисел. Формулы Эйлера для комплексных чисел. Сложение, вычитание, умножение, деление синусоидальных функций времени. Векторная диаграмма.
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной
тригонометрической или
алгебраической – формах.
Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
.
Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
| , | (4) |
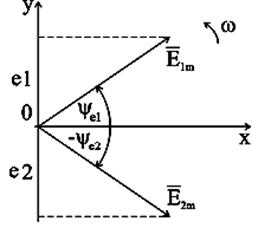
Рис.2.7. Векторное изображение синусоидальных ЭДС
Рис.2.8. Векторное изображение синусоидальных значений напряжения и тока, имеющих угол сдвига фаз
На рис. 2.9 и 2.10 показано сложение и вычитание векторов на векторных диаграммах. Здесь сложение двух синусоид и , представленных синусоидой , выполнено в виде сложения вращающихся векторов на декартовой плоскости . Аналогично выполняется вычитание векторов ЭДС .
Изображение синусоидальных величин на комплексной плоскости осуществляется комплексными числами.

Формула Эйлера:
Данная формула связывает комплексную экспоненту с тригонометрическими функциями:
Перевод комплексных чисел из одной формы в другую можно производить по следующим формулам:
;
;
При сложении и вычитании комплексных чисел удобно пользоваться алгебраической формой записи:
При умножении, делении, возведении в степень удобно пользоваться показательной формой
Если комплексное число , то комплексное число называется сопряженным комплексным числом.
Синусоидальное ЭДС можно представить комплексным числом:
Для напряжения и тока аналогично.
Рекомендуемые страницы:
lektsia.com
Закон Ома. Формула Закона Ома
Нужна помощь в написании работы?
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Георг Симон ОмЗакон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается в следующем виде:
где
I – сила тока в проводнике, единица измерения силы тока – ампер [А];
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
R – электрическое сопротивление проводника, единица измерения электрического сопротивления – ом [Ом].
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
Где и когда можно применять закон Ома?
Нужна помощь в написании работы?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Нужна помощь в написании работы?
zakon-oma.ru


