Полосовой фильтр схема – Электрические пассивные фильтры | Практическая электроника

Содержание

Полосовой фильтр на ОУ. Расчет полосового фильтра

Полосовые фильтры используются во многих областях электроники. Особенно они широко используется в схемах радиоприема и радиопередачи, в частности в резонансных контурах. Однако и для низких частот, активный полосовой фильтр является эффективным средством выделения сигнала промежуточных частот. Для этих фильтров наиболее широко используемым активным элементом является операционный усилитель (ОУ).

Полосовые фильтры на ОУ легко проектировать и строить, поскольку для этого необходимо минимум компонентов. В дополнение к этому, они обеспечивают очень высокий уровень производительности.

Что такое полосовой фильтр

Как следует из названия, полосовой фильтр фильтрует все частоты, пропуская только частоты находящиеся в определенном диапазоне. Все частоты за пределами данного частотного диапазона ослабляются.

Есть два основных параметра определяющие характеристики полосового фильтра: полоса пропускания, где фильтр пропускает сигналы и полоса затухания, в которой сигналы ослабляются.

Идеальный полосовой фильтр имеет ровную полосу пропускания (усиление и отсутствие затухания сигнала по всей полосе пропускания) и полное затухание вне полосы пропускания. Кроме того, переход из полосы пропускания абсолютно резкий.

Но на практике невозможно создать идеальный полосовой фильтр. Реальный фильтр неспособен полностью задержать все частоты за границами желаемого диапазона частот. В частности, имеется область в непосредственной близости у границы заданного диапазона, где сигнал частично ослабляется, но не отфильтровывается полностью. Эта область носит название крутизна спада фильтра, и измеряется в дБ затухания на октаву. Как правило, при проектировании, стремятся сделать данный спад как можно более узким, что позволяет получить фильтр максимально приближенным к заданным параметрам.

Расчет полосового фильтра

Расчет полосового фильтра может стать очень сложным занятием даже при использовании операционных усилителей. Тем не менее можно немного упростить методику расчета, и в то же время сохранить производительность полосового фильтра на ОУ на приемлемом уровне.

Данная схема и методика расчета представляют собой хороший баланс между производительностью и простотой конструкцией фильтра.

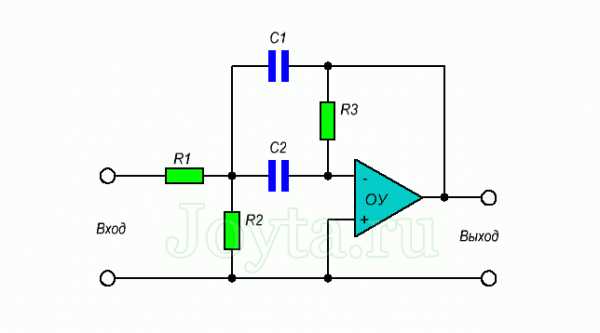
Из рисунка видно, что помимо операционного усилителя схема еще содержит два конденсатора и три резистора.

Пример упрощенного расчета элементов полосового фильтра на ОУ

Входные данные:

Резонансная частота f = 20Гц.
Добротность Q = 10.
Коэффициент передачи Hо = 5

Так как fmax – fmin = f / Q = 2Гц,

то полоса пропускания составит fmax = 21 Гц, fmin=19 Гц.

Будем исходить из того, что C1=C2=C=1мкФ

Тогда сопротивления резисторов можно рассчитать по следующим формулам:

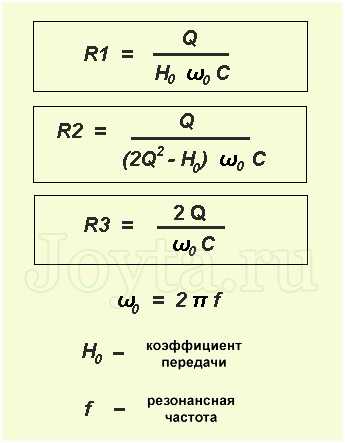
В нашем случае получим следующие результаты:

R1 = 10 / (5*2*3,14*20*0,000001) = 15,9 кОм

R2 = 10 / ((2*10*10-5)*2*3,14*20*0,000001) = 408 Ом

R3 = 2*10 / (2*3,14*20*0,000001) = 159,2 кОм

В схеме с одним операционным усилителем, желательно, чтобы коэффициент передачи не превышал 5 и добротность была не более 10. Для получения качественного фильтра параметры резисторов и конденсаторов должны как можно ближе соответствовать расчетным значениям.

www.joyta.ru

Самодельный антенный полосовой фильтр коротковолнового приёмника.

Фото 1.

Думаю, что у многих радиолюбителей было желание самому сделать приёмник коротковолнового диапазона, чтобы по параметрам он был не хуже профессионального. Сборку можно начать с входного устройства преселектора, точнее с антенного полосового фильтра.

Фильтр имеет полосу пропускания коротковолнового диапазона волн 1,5 – 30 МГц и используется во входной цепи профессиональных коротковолновых приёмников, имеющих высокую (35-100 МГц) первую промежуточную частоту. Его задача – подавить зеркальный и побочные каналы приёма, и тем самым повысить помехоустойчивость приёмного тракта и уменьшить излучение гетеродина в антенну. Его также можно использовать как антенный полосовой фильтр для подавления уровня индустриальных помех и помех от радиовещательных и телевизионных передатчиков, работающих вне коротковолнового диапазона. Это удобно, так как его входное и выходное сопротивление равно 50 Ом.

В профессиональных приёмниках диапазона КВ, благодаря применению аналогичного фильтра и использованию высокой промежуточной частоты, обеспечивается селективность по комбинационным каналам и ПЧ выше 100 дБ. На примере профессионального радиоприёмника WJ 8888 фирмы «Уоткинс Джонсон» (фото 1) широкополосный полосовой фильтр подключён к антенному входу приёмника. В разрыве между широкополосным фильтром и УВЧ на полевом транзисторе дополнительно присутствуют переключаемые узкополосные фильтры, которые перекрывают весь КВ диапазон.
Характеристики приёмника WJ 8888. Рабочий диапазон 0,5 – 30 МГц. Промежуточные частоты: 82,8 МГц, 10,7 МГц, 455 кГц. Чувствительность 0,56 мкВ при соотношении сигнал/шум 10 дБ. Входное волновое сопротивление 50 Ом. Селективность по побочным каналам приёма и каналу ПЧ составляет 100 дБ. В теории для приёмника с промежуточной частотой выше принимаемого сигнала достаточно иметь на входе только фильтр нижних частот.

Рис.1. Схема фильтра НЧ.

Рис. 2. АЧХ фильтра НЧ.

Однако в настоящее время нельзя забывать о помехах современных источников питания (компьютеров, импульсных преобразователях напряжений, беспроводных зарядок…), которые могут навестись в антенне, и перегрузить входные каскады приёмника. В этом случае положение спасёт фильтр верхних частот.

Рис. 3. Схема фильтра ВЧ.

Рис. 4. АХЧ фильтра ВЧ

Если соединить два фильтра вместе, то получится полосовой фильтр.

Рис 5. Полосовой антенный фильтр КВ приёмника.

Схема этого фильтра (рис. 5) приводится в книге О. В. Головина «Профессиональные радиоприёмные устройства декаметрового диапазона». 1985 г. Москва «Радио и связь».

Фото 2. Конструкция полосового антенного фильтра (рис. 5) коротковолнового приёмника.

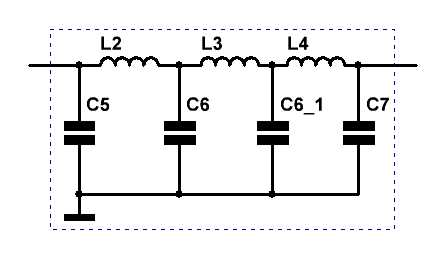
Когда то такой фильтр был мною собран, но сегодня меня не устроило его ослабление вне полосы пропускания, ведь самодельный приёмник должен быть лучше профессионального. После консультации со знакомыми радиолюбителями была предложена другая схема полосового фильтра, которую впоследствии я воплотил в жизнь. Схема фильтра Чебышева второго типа.

Рис. 6. Полосовой антенный фильтр коротковолнового приёмника.

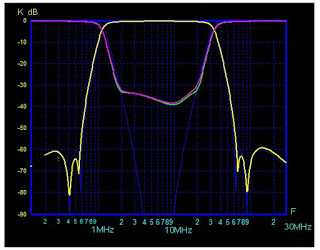Контура L2C2, L5C5, L8C8 настроены в резонанс на частоты 6,2 МГц, 6,0 МГц, 6,6 МГц соответственно. Они отвечают за неравномерность в полосе пропускания фильтра. Режекторные контура (фильтры-пробки) L3C3, L6C6 настроены в резонанс ниже полосы пропускания фильтра на частоты 550 кГц и на 410 кГц. Они ослабляют эти частоты и формируют крутизну среза (нижнюю границу) фильтра. Режекторные контура (фильтры-пробки) L4C4, L7C7 настроены в резонанс на частоты 66 МГц и 88 МГц. Также формируют верхнюю частоту среза.

Рис. 7. АЧХ фильтра.

Сама схема фильтра рассчитана в программе и соответствует характеристике на рисунке 7, при условии, что все элементы схемы имеют добротность 50, а номиналы катушек индуктивности и конденсаторов имеют стандартные величины, которые приведены на рисунке фильтра.

Характеристики самодельного фильтра. Полоса пропускания 1,5 – 30 МГц. Ослабление в полосе пропускания 0,5 дБ. Входное и выходное волновое сопротивление 50 Ом. Реальная АЧХ фильтра приведена на рисунке 8 (белая линия).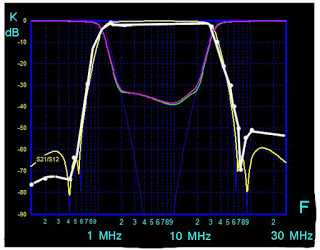

Рис. 8. Реальная АЧХ полосового фильтра.

Конструкция фильтра. Для монтажа я использовал катушки индуктивности с номиналами 3,9 – 68 мкГн и конденсаторы типа SMD. Не все номиналы деталей были в наличии. Так 3,9 мкГн заменил на 3,3 мкГн, а 15 мкГн сложил из двух последовательно соединённых 5,6 + 10 = 15,6 (мкГн) катушек с такими номиналами. L1 – 120нГн – 8 витков, L4 – 390 нГн – 14 витков, L7 – 330 нГн – 12 витков – намотаны проводом 0,5 мм на оправке 4 мм. L2 – 5,6 мкГн, L3 – 47 мкГн, L5 – 3.9 мкгн, L6 – 68 мкгн, L8 – 15 мкГн. С1, С 9 – 5600 пФ, С2 – 120 пФ, С3 – 1800 пФ, С4 – 15 пФ, С5 – 180 пФ, С6 – 2200 пФ,

С7 – 10 пФ, С8 – 39 пФ.

Макетная плата полосового антенного фильтра.

dedclub.blogspot.com

Самодельный полосовой фильтр FM диапазона (87,5 – 108 МГц) и рамочная антенна.

Бывают такие радиоприёмники и такие места, где любимая радиостанция едва пробивается с шумом, треском, хрипотой и рокотом помех. Один из симптомов – это перегрузка приёмного тракта мощным передатчиком, работающим вне радиовещательного диапазона приемника, а так же влияние индустриальных помех от работающих электродвигателей, генераторов и импульсных преобразователей напряжений.

Исправить положение поможет полосовой фильтр на входе приёмника или антенна, а может симбиоз из фильтра и антенны. Поэтому, предлагаю собрать полосовой фильтр на диапазон FM, а затем смастерить малогабаритную антишумовую антенну.

Полосовой фильтр на частоту 87,5 – 108 МГц.

В современных бытовых приемниках, как правило, на входе уже стоит полосовой фильтр, выполненный на ПАВ (фильтр поверхностных волн). Однако нет большего удовольствия, чем собрать аналогичный полосовой фильтр на дискретных элементах и сравнить их характеристики, тем более что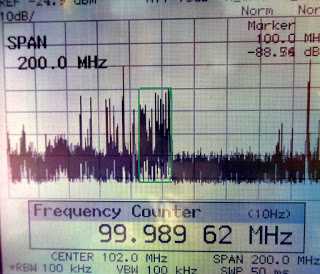 режекторный полосовой заградительный фильтр на этот диапазон уже был создан раньше в этом блоге. Это уже не первый фильтр, который я собрал, а его особенность – это хорошая повторяемость, минимальные потери в полосе пропускания (не более 2 дБ) и достаточно большое ослабление вне полосы пропускания приёмника (до 70 дБ в коротковолновом диапазоне). Аналогичный фильтр я применил в самодельном приёмнике с двойным преобразованием частоты, вот уже два года этот экземпляр безукоризненно трудится на даче. Здесь же я решил продлить и расширить тему, несколько улучшив параметры фильтра. Теперь можно уже забыть о влиянии мощных коротковолновых передатчиках соседей-радиолюбителей. Настраиваюсь радиоприёмником на радиостанцию, которая в отличие от других сопровождается потрескиванием и шумом. Подсоединяю в разрыв меду антенной (проволока, равная четвёртой части длины волны, что составляет 75 см) и входом приёмника полосовой фильтр, и шум и потрескивание пропадают. Казалось, что фильтр должен ослабить чувствительность на пару децибел и радиостанция должна полностью утонуть в хаосе помех, но произошло обратное явление, и радиопередача вынырнула на поверхность, освобождаясь от них.

Фото 1.

На экране анализатора спектра (фото 1) видны все радиостанции в полосе пропускания прибора, которая составляет 200 МГц. Это телевизионные, радиовещательные и коротковолновые радиостанции, а так же помехи проводных модемов. Полоса диапазона FM выделена зелёным прямоугольником. В Москве и в Подмосковье в этой полосе частот работают более 40 радиостанций.

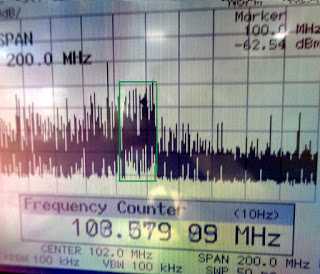Фото 2.

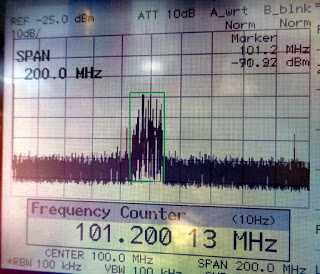Теперь рядом с антенной я кладу батарейную дрель и нажимаю на курок. Еле видимые глазом искорки от контактных щёток дрели излучают помехи в широком диапазоне волн. Пейзаж на экране резко изменился (фото 2). Теперь помимо радиостанций в полосе приёма дополнительно присутствует масса несущих частот от искрящихся щёток моторчика. Бюджетному приёмнику переварить такой пейзаж не под силу.

Фото 3.

Картина выглядит совсем иначе (фото 3), когда по входу стоит полосовой фильтр. На экране анализатора спектра полный штиль и только как фарватер открыт диапазон FM. Волна даже не шелохнётся, если я нажму на курок электродрели.

Схема полосового фильтра.

Рис 1. Схема полосового фильтра.

Конструкция фильтра.

Фото 4. Макет полосового фильтра.

Фильтр выполнен на одностороннем фольгированном стеклотекстолите. Все катушки наматываются проводом диаметром 1 мм на оправке 5 мм и содержат по 2 витка (L3, L4, L5) и 12 витков (L1, L2). C1, C2 – 10 пФ, С3, С5 – 82 пФ, С4 – 120 пФ. Характеристики фильтра.

Входное и выходное сопротивление фильтра 50 Ом. Затухание в полосе пропускания фильтра – 2 дБ. Полоса пропускания по уровню 2,5 дБ составляет 82 – 110 МГц. Неравномерность в полосе пропускания 1 дБ. Ослабление на частотах 30 – 50 МГц – не менее 70 – 60 дБ, а на частоте 150 МГц – не менее 50 дБ.

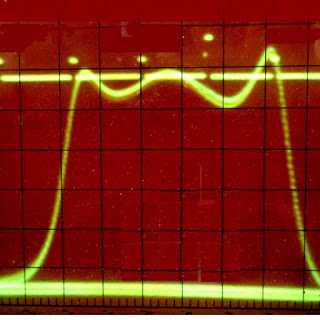Фото 5. АЧХ полосового фильтра.

Антишумовая антенна.

Особенность диапазона 87, 5 – 108 МГц – это широкая полоса принимаемых частот, которая составляет 20,5 МГц. Антенна в виде проволоки размером, равным четвёртой части длины волны (75 см), на предельной дальности приёма, перекроет только половину диапазона. Лучше в этом случае поведёт себя телескопическая антенна, размер которой можно скорректировать на краях диапазона. Но обе антенны ведут себя крайне плохо в условиях сильных помех. Время вспомнить о рамочной антенне. Прежде всего, это параллельный колебательный контур, настроенный в резонанс и как всякая замкнутая система он способен ослаблять помехи, то есть работать также как и полосовой фильтр. Достоинство такой антенны – это маленькие габариты. Однако от этих самых габаритов нельзя ожидать хороших результатов по дальности приёма, хотя её усиление не хуже телескопической антенны, правда, только на отдельном участке диапазона, исключительно из-за своей узкой полосы резонанса, которая составляет около 10 МГц. Таким образом, перекрывая только половину FM диапазона, она всё же работает лучше, а иначе бы не назвал бы её антишумовой антенной.

Рис 2. Схема антенны с согласующим устройством.

Конструкция антенны.

Фото 6. Заготовки из пивной алюминиевой баночки.

Для изготовления такой антенны мне потребовалась алюминиевая баночка из-под пива. Весь её расчёт состоял в раскрое материала на части для изготовления конструкции похожей на квадрат (в идеале рамка должна быть круглой, а её рекомендуемый периметр обычно составляет 10 часть длины волны). В качестве материала так же годится медь, латунь, фольгированный стеклотекстолит. В старых ламповых приёмниках с УКВ диапазоном антенна была помещена внутри корпуса лампового агрегата. Теперь самодельная рамочная антенна, размещена на задней крышке, что вполне приемлемо для носимого или настольного варианта приёмника.

Фото 7. Макет рамочной антенны. L 1 – провод диаметром 1 мм, 5 витков намотаны на оправке диаметром 5,7 мм.
С1, С2 – конденсаторы подстроечные. С 1 – 5/30 пФ (15 пФ). С 2 – 2/10 пФ (3 пФ)

Убедившись, что такая антенна реально работает и без фильтра, останется только сделать рамочную широкополосную антенну, которая перекрыла бы весь диапазон FM. Но об этом в следующем посте.

Фото 8.

dedclub.blogspot.com

Операционные усилители (на основе простейших примеров): часть 3 / Habr

Краткое введение

Продолжаю ~~спамить~~ писать на тему операционных усилителей. В этой статье постараюсь дать обзор одной из важнейших тем, связанной с ОУ. Итак, добро пожаловать, активные фильтры.

Обзор темы

Возможно, Вы уже сталкивались с моделями RC-, LC- и RLC-фильтров. Они вполне подходят для большинства задач. Но для некоторых целей очень важно иметь фильтры с более плоскими характеристиками в полосе пропускания и более крутыми склонами. Вот тут нам и нужны активные фильтры.
Для освежения в памяти, напомню, какие бывают фильтры:
Фильтр Нижних Частот (ФНЧ) — пропускает сигнал, который ниже определенной частоты (ее еще именуют частотой среза). Википедия
Фильтр Высоких Частот (ФВЧ) — пропускает сигнал выше частоты среза. Википедия
Полосовой Фильтр — пропускает только определенный диапазон частот. Википедия
Режекторный Фильтр — задерживает только определенный диапазон частот. Википедия
Ну еще немного лирики. Посмотрите на амплитудно-частотную характеристику (АЧХ) ФВЧ. На этом графике ничего интересного пока не ищите, а просто обратите внимание на участки и их названия:

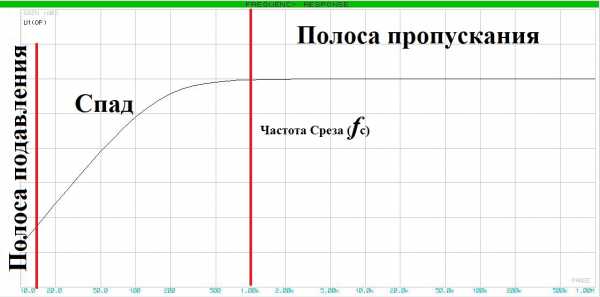
Самые банальные примеры активных фильтров можно подсмотреть здесь в разделе «Интеграторы и дифференциаторы». Но в данной статье эти схемы трогать не будем, т.к. они не очень эффективны.

Выбираем фильтр

Предположим, что Вы уже определились с частотой, которую хотите фильтровать. Теперь нужно определиться с типом фильтра. Точнее нужно выбрать его характеристику. Иными словами, как фильтр будет себя «вести».
Основными характеристиками являются:
Фильтр Баттерворда — обладает самой плоской характеристикой в полосе пропускания, но имеет плавный спад.
Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
Фильтр Бесселя — имеет хорошую фазочастотную характеристику и вполне «приличный» спад. Считается лучшим выбором, если нет специфического задания.

Еще немного информации

Предположим, и с этим заданием вы справились. И теперь можно смело приступить к расчетам.
Есть несколько методов расчета. Не будем усложнять и воспользуемся самым простым. А самый простой — это «табличный» метод. Таблицы можно найти в соответствующей литературе. Чтобы Вы долго не искали, приведу из Хоровица и Хилла «Искусство Схемотехники».
Для ФНЧ:

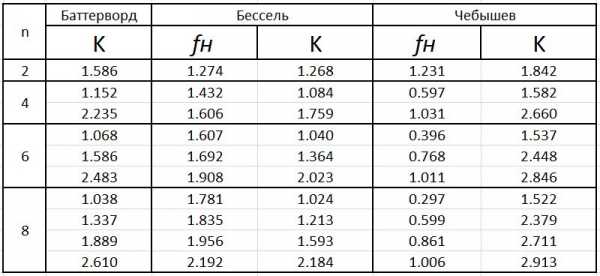
Скажем так, это все Вы могли бы найти и прочитать и в литературе. Перейдем конкретно к проектированию фильтров.

Расчет

В данном разделе попытаюсь кратко «пробежаться» по всем типам фильтров.
Итак, задание # 1. Построить фильтр низких частот второго порядка с частотой среза 150 Гц по характеристике Баттерворда.
Приступим. Если мы имеем фильтр n-ного четного порядка, это означает, что в нем будет n/2 операционников. В данном задании — один.
Схема ФНЧ:

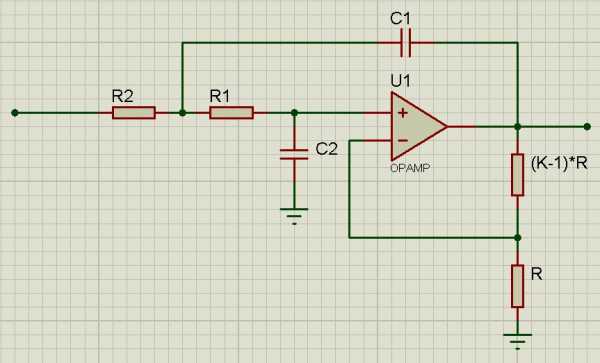
Для данного типа расчета берется во внимание, что R1 = R2, C1 = C2.
Смотрим в табличку. Видим, что К = 1.586. Это нам пригодится чуть позже.
Для фильтра низких частот справедливо:
, где, разумеется,
— это частота среза.
Сделав подсчет, получаем . Теперь займемся подбором элементов. С ОУ определились — «идеальный» в количестве 1 шт. Из предыдущего равенства можно предположить, что нам не принципиально, какой элемент выбирать «первым». Начнем с резистора. Лучше всего, чтоб его значение сопротивления были в пределах от 2кОм до 500кОм. На глаз, пусть он будет 11 кОм. Соответственно, емкость конденсатора станет равной 0.1 мкФ. Для резисторов обратной связи значение R берем произвольно. Я обычно беру 10 кОм. Тогда, для верхнего значение К возьмем из таблицы. Следовательно, нижний будет иметь значение сопротивления R = 10 кОм, а верхний 5.8 кОм.
Соберем и промоделируем АЧХ.

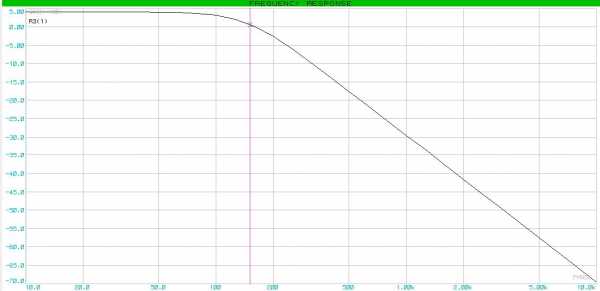
Задание # 2. Построить фильтр высоких частот четвертого порядка с частотой среза 800 Гц по характеристике Бесселя.
Решаем. Раз фильтр четвертого порядка, то в схеме будет два операционника. Тут все совсем не сложно. Мы просто каскадно включаем 2 схемы ФВЧ.
Сам фильтр выглядит так: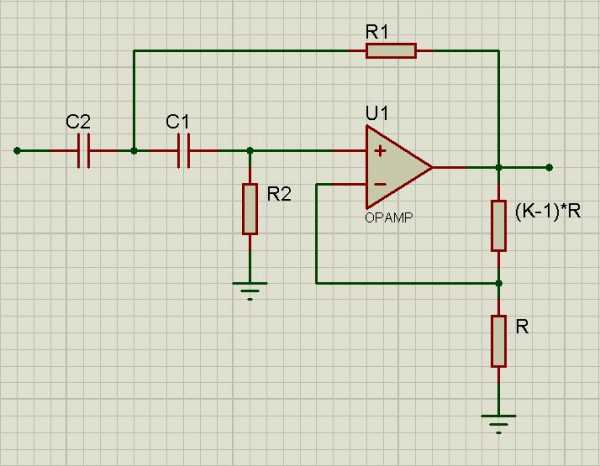

Фильтр же четвертого порядка выглядит: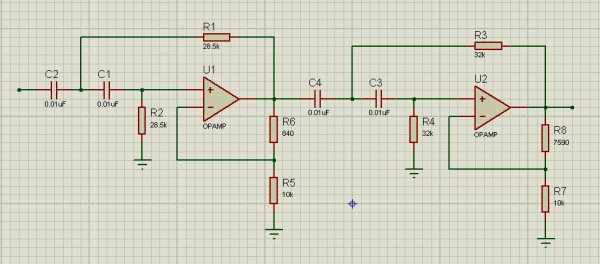

Теперь расчет. Как видим, для фильтра четвертого порядка у нас аж 2 значения К. Логично, что первое предназначается для первого каскада, второе — для второго. Значения К равны 1.432 и 1.606 соответсвенно. Таблица была для фильтров низких частот (!). Для расчета ФВЧ надо кое-что изменить. Коэффициенты К остаются такими же в любом случае. Для характеристик Бесселя и Чебышева изменяется параметр
— нормирующая частота. Она будет равна теперь:

Для фильтров Чебышева и Бесселя как для нижних частот, так и для высоких справедлива одна и та же формула:

Учтите, что для каждого отдельного каскада придется считать отдельно.
Для первого каскада:

Пусть С = 0.01 мкФ, тогда R = 28.5 кОм. Резисторы обратной связи: нижний, как обычно, 10 кОм; верхний — 840 Ом.
Для второго каскада:

Емкость конденсатора оставим неизменной. Раз С = 0.01 мкФ, то R = 32 кОм.
Строим АЧХ.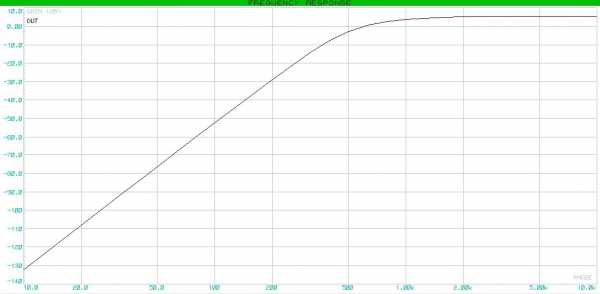

Для создания полосового или режекторного типа фильтров можно каскадно соединить ФНЧ и ФВЧ. Но такими типами, зачастую, не пользуются из-за плохих характеристик.
Для полосовых и режекторных фильтров также можно использовать «табличный метод», но тут немного другие характеристики.
Приведу сразу табличку и немного ее объясню. Чтоб сильно не растягивать — значения взяты сразу для полосового фильтра четвертого порядка.

a1 и b1 — расчетные коэффициенты. Q — добротность. Это новый параметр. Чем значение добротности больше — тем более «резким» будет спад. Δf — диапазон пропускаемых частот, причем выборка идет на уровне -3 дБ. Коэффициент α — еще один расчетный коэффициент. Его можно найти используя формулы, которые довольно легко найти в интернете.
Ну ладно, хватит. Теперь рабочее задание.
Задание # 3. Построить полосовой фильтр четвертого порядка по характеристике Баттерворда с центральной частотой 10 кГц, шириной пропускаемых частот 1 кГц и коэффициентом усиления в точке центральной частоты равным 1.
Поехали. Фильтр четвертого порядка. Значит два ОУ. Типовую схему приведу сразу с расчтными элементами.

Для первого фильтра центральная частота определяется как:

Для второго фильтра:

Конкретно в нашем случае, опять же из таблицы, определяем, что добротность Q = 10. Рассчитываем добротность для фильтра. Причем, стоит отметить, что добротность обоих будет равна.

Поправка усиления для области центральной частоты:

Финальная стадия — расчет компонентов.
Пусть конденсатор будет равен 10 нФ. Тогда, для первого фильтра:

В том же порядке, что и (1) находим R22 = R5 = 43.5 кОм, R12 = R4 = 15.4 кОм, R32 = R6 = 54.2 Ом. Только учтите, что для второго фильтра используем
Ну и на последок, АЧХ.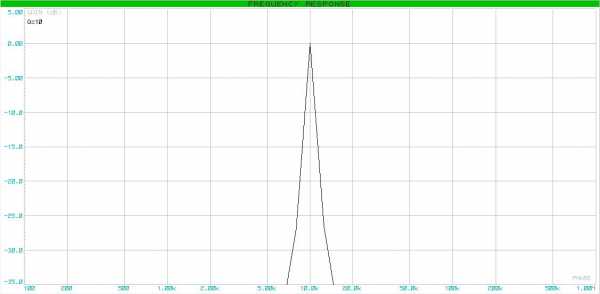

Следующая остановка — полосно-заграждающие фильтры или режекторные.
Тут есть несколько вариаций. Наверное, самый простой — это фильтр Вина-Робинсона (англ. Active Wien-Robinson Filter). Типовая схема — тоже фильтр 4го порядка.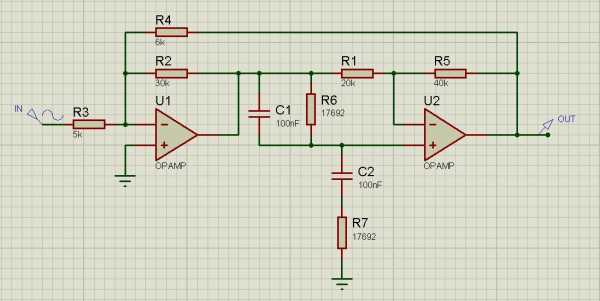

Наше последнее задание.
Задание # 4. Построить режекторный фильтр с центральной частотой 90 Гц, добротностью Q = 2 и коэффициентом усиления в полосе пропускания равным 1.
Прежде всего, произвольно выбираем емкость конденсатора. Допустим, С = 100 нФ.
Определим значение R6 = R7 = R:

Логично, что «играясь» с этими резисторами, мы можем изменять диапазон частот нашего фильтра.
Далее, нам надо определить промежуточные коэффициенты. Находим их через добротность.

Выберем произвольно резистор R2. В данном конкретном случае, лучше всего, чтобы он равнялся 30 кОм.
Теперь можем найти резисторы, которые будут регулировать коэффициент усиления в полосе пропускания.

И на последок, необходимо произвольно выбрать R5 = 2R1. У меня в схеме эти резисторы имеют значение 40 кОм и 20 кОм соответственно.
Собственно, АЧХ: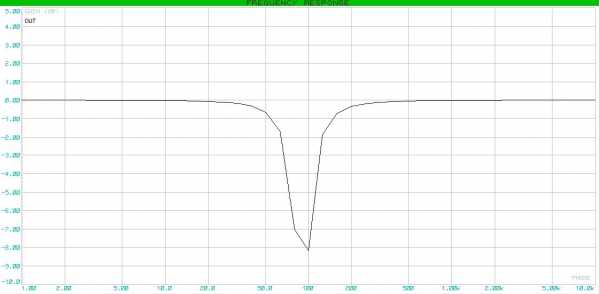

Практически конец

Кому интересно узнать немного больше, могу посоветовать почитать Хоровица и Хилла «Искусство схемотехники».
Также, D. Johnson «A handbook of active filters».
Википедия
Также, кому не очень нужны расчеты, а нужны именно сами фильтры, могу посоветовать полезный софт
P.S. Добавлю очень полезную ссылку и ее зеркало. За линк спасибо spiritus_sancti

habr.com

9. Полосовой фильтр и режекторный фильтр

ЭКСПЕРИМЕНТ 24 Полосовой фильтр и режекторный фильтр

Цели

После проведения данного эксперимента Вы сможете продемонстрировать работу индуктивно-емкостного полосового фильтра и резистивно-емкостного режекторного фильтра.

Необходимые принадлежности

* Осциллограф

* Цифровой мультиметр

* Макетная панель

* Генератор функции

* Элементы:

четыре конденсатора 0,1 мкФ, один конденсатор 0,47 мкФ, одна катушка индуктивности 10 мГн, один резистор 100 Ом, четыре резистора 15 кОм.

ВВОДНАЯ ЧАСТЬ

Полосовой фильтр — это частотночувствительная схема, которая пропускает узкий диапазон. частот в окрестности центральной резонансной частоты (fr)

Все другие частоты ниже или выше узкой полосы пропускания значительно подавляются. Типичная характеристика полосового фильтра показана на рисунке 24-1А.

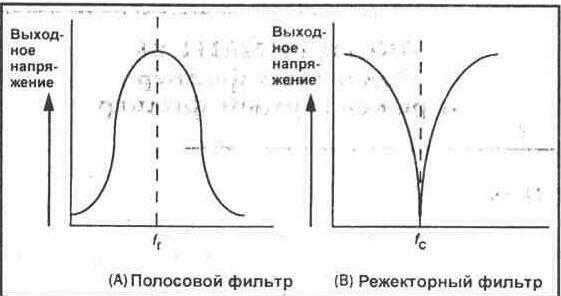
Рис. 24-1.

Режекторный фильтр представляет собой противоположность полосовому фильтру. Он подавляет или устраняет сигналы, частоты которых попадают в узкий диапазон с центральной частотой fc. Все частоты выше и ниже центральной частоты фильтр пропускает с минимальным ослаблением (см. рис. 24-1 В). Режекторный фильтр иногда называют вырезающим фильтром, поскольку этот фильтр используется для вырезания или режекции мешающего сигнала одной частоты.

Краткое содержание

Имеется несколько различных способов схемной реализации полосового фильтра и режекторного фильтра. Индуктивно-емкостные резонансные схемы могут комбинироваться различными методами для создания обоих типов фильтров. В данном эксперименте Вы познакомитесь с полосовым фильтром.

Режекторный фильтр может быть реализован и на базе индуктивно-емкостных схем. Однако в данном эксперименте Вы познакомитесь с популярным и широко используемым двойным Т-образным мостовым фильтром. Это резистивно-емкостной режекторный фильтр, способный подавлять определенную частоту и частоты в ее окрестности. Центральная частота рассчитывается при помощи следующей формулы:

fp = 1/2*3.14RC

Поскольку у Вас нет удобных средств для точного измерения частоты, Вы будете просто варьировать частоту, генерируемую генератором функций, и отмечать при помощи мультиметра выходную характеристику фильтра. Таким образом, можно увидеть, как выходное напряжение изменяется в зависимости от частоты как в случае полосового фильтра, так и в случае режекторного фильтра.

ПРОЦЕДУРА

1. Обратитесь к рисунку 24-2. Соберите эту схему полосового фильтра на Вашей макетной панели. Выходное напряжение генератора функций прикладывается к конденсаторам, тогда как выходное напряжение фильтра снимается с резистора 1000м. Заметьте, что общая емкость схемы составлена из двух конденсаторов с емкостью 0,47 мкФ и 0,1 мкФ.

2. Используя значения, показанные на рисунке 24-2, рассчитайте общую емкость схемы и резонансную частоту данной схемы.

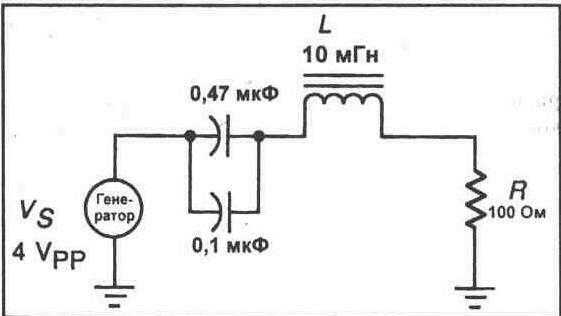
Рис. 24-2.

Сt = _______ мкФ

fr=_____Гц

3. Установите регулятором амплитуды генератора функций выходное напряжение размаха 4 В:

Затем установите частоту приблизительно 500 Гц.

4. Подключите осциллограф параллельно выходному резистору 1000м. Медленно увеличивайте частоту на выходе генератора функций и наблюдайте за изменением выходного напряжения схемы. Замечайте вариацию этого напряжения. Изменения частоты выполняйте медленно, чтобы Вы могли получать хорошую индикацию того, как изменяется напряжение, когда частота увеличивается или понижается. Увеличивайте частоту приблизительно до 5 кГц.

5. Регулируйте частоту, наблюдая за выходом фильтра. Настройте генератор функций на пиковое выходное напряжение. Заметьте по генератору функций или измерьте период и частоту при помощи осциллокрафа. f=____Гц

6. Объясните изменения, которые Вы наблюдали в шагах 4 и 5.

7.Демонтируйте .полосовой фильтр. Вместо него соберите схему двойного Т-образного мостового фильтра, который показан на рисунке 24-3. Будьте внимательны при монтаже схеме, поскольку она несколько сложна, и легко можно сделать ошибку во время монтажа.

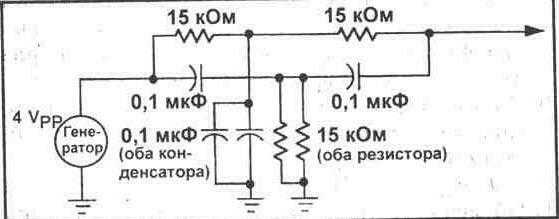
Рис. 24-3.

Имеется несколько-важных моментов, которые Вы должны принять во внимание при монтаже данной схемы. Во-первых, значение одного (общего) конденсатора получается комбинированием емкостей двух параллельных конденсаторов 0,1 мкФ. Вспомните, что емкости параллельных конденсаторов складываются, образуя, следовательно. один конденсатор емкостью 0,2 мкФ. Другое значение в данной схеме получается соединением двух параллельных резисторов. Два параллельных резистора с одинаковым сопротивлением имеют общее сопротивление, равное половине сопротивления одного из резисторов. В данном случае два резистора 15 кОм соединены параллельно, чтобы получить сопротивление 7,5 кОм.

8. Используя значения, показанные на рисунке 24-3, рассчитайте частоту режекции или центральную частоту данного фильтра. fc=_____Гц

9. Настройте генератор функций на частоту 10 Гц и размах напряжения 4В. Подключите осциллограф на выход фильтра. Увеличивайте теперь выходную частоту приблизительно до 1000 Гц и наблюдайте за вариацией выходного напряжения фильтра. Повторяйте это несколько раз, чтобы Вы могли наверняка увидеть эффект.

10.Настройте генератор функций на нулевую частоту (минимальное напряжение). Измерьте частоту и запишите. f=_____Гц

11.Объясните полученные Вами результаты в шагах 9 и 10.

ОБЗОРНЫЕ ВОПРОСЫ

1. Режекторный фильтр может быть реализован на базе индуктивно-емкостных схем:

а) высказывание истинно,

б) высказывание ложно.

2. В индуктивно-емкостном полосовом фильтре центральная частота определяется значениями:

а) приложенного напряжения,

б) L и R,

в) R и С,

г) L и С.

3. Полосовой фильтр пропускает:

а) одну частоту,

б) только высокие частоты,

в) узкую полосу частот,

г) все частоты.

4. Двойной Т-образный мостовой фильтр представляет собой:

а) полосовой фильтр,

б) фильтр нижних частот,

в) фильтр верхних частот,

г) режекторный фильтр.

5. Какова центральная частота двойного Т-образного мостового фильтра при значениях R = 10 кОм и С = 0,47 мкФ?

а) 34 Гц,

б) 47 Гц,

в) 68 Гц,

г) 120 Гц.

lib.qrz.ru

Диапазонные полосовые фильтры. Схема ДПФ для трансиверов и радиопрёмников.

Рис. 1

Поскольку вход у нас низкоомный и должен быть согласован с 50-омным волновым сопротивлением коаксиального кабеля, выбор пал на схему усилителя с общей базой на транзисторе Т1, обладающую на высоких частотах известными преимуществами перед схемой с общим эмиттером.

Переменный резистор R2 позволяет выставить желаемый коэффициент передачи ДПФов в пределах 0 – 6 дБ. Входное сопротивление устройства при этом составляет величину 53-65 Ом, в зависимости от положения регулятора, что для приёмной аппаратуры находится во вполне допустимом диапазоне.

Приемлемые динамические характеристики входного усилителя достигаются 3-мя инструментами:
1. достаточно высоким током покоя транзистора Т1;
2. введением катушки (дросселя) L1 для притягивания напряжения коллектора Т1 к нулевой точке;
3. уходом от традиционных 50-омных характеристических сопротивлений фильтров в пользу более высоких значений, что позволяет транзистору работать на более высокоомную нагрузку, что в свою очередь определяет и лучшие динамические показатели.

Выходное сопротивление первого каскада определяется номиналом резистора R7 и составляет 470 Ом. Исходя из этой величины, и следует рассчитывать характеристические сопротивления полосовых фильтров.
Уход от 50-омной схемотехники позволяет, помимо всего прочего, и снизить требования к параметрам катушек, входящих в состав фильтров, и обратить свой взор в сторону маленьких китайских дроссельков.

Выходному каскаду живётся, с одной стороны легче, чем входному, ведь на его вход поступает уже отфильтрованный сигнал и, соответственно, меньшей амплитуды, но с другой стороны работает он на 50-омную нагрузку, и простым увеличением тока покоя транзистора не удастся обеспечить приемлемого значения ДД (вернее удастся, но значение этого тока составит неприличную величину). Именно поэтому, в качестве выходного и был выбран двухтактный каскад на комплементарных транзисторах.

Расчёт полосовых фильтров будем производить с помощью таблицы ссылка на таблицу.

Глядя на схему, закрадываются смутные сомнения в необходимости дросселя L1, ведь с функцией подтягивания коллекторного напряжения Т1 к нулевой точке прекрасно должны справиться катушки, входящие в состав фильтра.
Правильно закрадываются! Отлично справятся, поэтому, если не будут раздражать щелчки во время переключения диапазонов – смело выкидывайте.

В качестве переключателя диапазонов вполне можно использовать и механические устройства, и диоды шоттки, и электронные ключи, но куда правильнее для этих целей будет задействовать радиочастотные реле, с замыканием незадействованных фильтров на землю.

Приведём результаты расчётов.

Диапазон (МГц)	L2 (мкГн)	L3 (мкГн)	L4 (мкГн)	С5 (пФ)	С6 (пФ)	С7 (пФ)
1,70 – 2,50	10,5	107	10,5	569	56	569
2,50 – 3,70	7,2	71	7,2	380	38,5	380
3,70 – 5,60	5,1	45	5,1	240	27,2	240
5,60 – 8,10	3	34	3	182	16,3	182
8,10 – 12,1	2,3	21,3	2,3	114	12,1	114
12,1 – 18,2	1,54	14	1,54	75	8,2	75
18,2 – 30,0	1,2	7,2	1,2	39	6,4	39

Представленные диапазонные фильтры полностью перекрывают КВ диапазон, обеспечивают неравномерность АЧХ внутри диапазона не более 0,5 дБ и крутизну спада вне полосы пропускания – 43 дБ/октаву.

Теперь, что касается владельцев SDR-ов и приёмников прямого преобразования. Для них важен параметр подавления паразитных каналов приёма на нечётных гармониках. Приведу эти цифры для SSB радиолюбительских диапазонов.

Диапазон	Подавление приёма на 3-й гармонике (дБ)	Подавление приёма на 5-й гармонике (дБ)	Подавление приёма на 7-й гармонике (дБ)
80-метровый	53	68	78
40-метровый	53	68	78
30-метровый	50	65	74
20-метровый	47	63	72
15-метровый	40	56	65
10-метровый	50	65	74

С учётом того, что и сам смеситель обеспечивает меньший уровень передачи гармониковых сигналов децибел на 10-15, в принципе, получается приличное подавление.
Ну а для обладателей ключевых смесителей с динамическим диапазоном 110-115 дБ цифры эти могут показаться недостаточными – им подавай как минимум 80 дБ.

Ну и ничего страшного, даже количество катушек не придётся увеличивать, просто заменим полосовые фильтры на ФНЧ 7-го порядка.

Рис.2

Расчёт фильтров нижних частот проведём с помощью другой таблицы ссылка на таблицу.

Диапазон (МГц)	L2 (мкГн)	L3 (мкГн)	L4 (мкГн)	С5 (пФ)	С6, С6_1 (пФ)	С7 (пФ)
1,70 – 2,50	37,6	40,2	37,6	235	357	235
2,50 – 3,70	25,4	27,2	25,4	159	241	159
3,70 – 5,60	16,8	18	16,8	105	160	105
5,60 – 8,10	11,6	12,4	11,6	73	110	73
8,10 – 12,1	7,8	8,3	7,8	49	74	49
12,1 – 18,2	5,2	5,5	5,2	32	49	32
18,2 – 30,0	3,1	3,4	3,1	20	30	20

Диапазон	Подавление приёма на 3-й гармонике (дБ)	Подавление приёма на 5-й гармонике (дБ)	Подавление приёма на 7-й гармонике (дБ)
80-метровый	89	121	142
40-метровый	89	121	142
30-метровый	86	118	140
20-метровый	83	115	136
15-метровый	76	108	129
10-метровый	86	118	140

Если и этого мало – прямая дорога к эллиптическим фильтрам Кауэра ссылка на таблицу.

Теперь, что касается элементов.
Если нет особого желания ковыряться с подстроечными конденсаторами и высокочастотным АЧХ-ометром, рекомендую обзавестись недорогим китайским измерителем емкостей и индуктивностей и подобрать номиналы элементов в фильтрах с точностью 3-5%. Параллельные и последовательные соединения никак не возбраняются.

К дросселю L1 следует отнестись с определённой долей уважения – его индуктивность должна значительно превышать индуктивности катушек L2, а собственная ёмкость быть значительно ниже значений конденсаторов С5.
Готовым дроссельком здесь не обойтись, поэтому намотать его придётся самостоятельно на низкочастотном тороидальном феррите М2000. Количество витков 10-15, рассчитывается в программе Coil32 в зависимости от размеров кольца.

Настройка схемы сводится к установке токов покоя транзисторов в пределах 15мА. Делается это подбором соответствующих резисторов – R6 и R11.
Если выходное напряжение в точке соединения R15 и R16 будет сильно отличаться от указанного на схеме – придётся поиграться номиналом резистора R10 или R13.

vpayaem.ru

Расчёт активных фильтров. Онлайн калькулятор.

И начнём мы с активных фильтров нижних частот (ФНЧ) и фильтров верхних частот (ФВЧ) 2-го и 3-го порядков имени товарищей Бесселя, Баттерворта и Пафнутия нашего Чебышева.

Эко нас понесло! Почему бы не удовлетвориться одним учёным мужем? К примеру, привычный с детства Баттерворт совсем не плох, к тому же широко известен в узких кругах.

Согласен, с какой стороны не возьми, Баттерворт – хорошая штука. Тут тебе и максимально гладкая АЧХ на частотах полосы пропускания, и приличный спад характеристики в полосе подавления, однако…
Если на первый план выдвигается линейность фазо-частотной характеристики в полосе пропускания фильтра (например, в аудио-кроссоверах), то пальма первенства в АЧХ-строении переходит к обратному многочлену профессора Фридриха Вильгельма Бесселя, ну а если ФЧХ нам до фени, а в приоритете максимально крутой спад характеристики на частотах полосы подавления, то как ни крути, придётся с головой окунуться в полиномы Пафнутия Львовича Чебышёва.

Фильтры построим на основе повторителей, они просты в расчётах, к тому же легко могут быть реализованы не только на операционных усилителях, но и на транзисторах.

А желающим спроектировать активный фильтр нижних частот 3-6-го порядка с перестраиваемой частотой среза, следует посетить страницу ссылка на страницу .

Рис.1

На Рис.1 приведены схемы активных фильтров нижних частот (ФНЧ) 2-го и 3-го порядка на ОУ и, для примера, реализация фильтра на биполярном транзисторе, отличающаяся от схем на операционниках только наличием двух резисторов, задающих необходимое напряжение смещения на базе.

Крутизна спада АЧХ этих фильтров в полосе подавления для Бесселя – около 5 дБ/октаву на каждый порядок фильтра, для Баттерворта – 6 дБ/октаву и около 8 дБ/октаву для Чебышёва.
Коэффициент передачи в полосе пропускания К=1, а номиналы рассчитываются исходя из формул:
C1=К_С1/(2π*F*R) &nbsp C2=К_С2/(2π*F*R) &nbsp C3=К_С3/(2π*F*R), где коэффициенты К_С1, К_С2 и К_С3 зависят как от порядка фильтра, так и от его принадлежности к той или иной фамилии.
К примеру для фильтров Баттерворта 2-го порядка К_С1=1,114, К_С2=0,707, а для фильтров Баттерворта 3-го порядка К_С1=1,393, К_С2=3,549, К_С3=0,202.

Критерии выбора величины сопротивления R, такие же, как и в пассивных фильтрах, она должна быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного сопротивления ОУ или ЭП (на практике 1-100 кОм).

РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНЫХ ФНЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА

Плавно переходим к активным фильтрам верхних частот (ФВЧ) 2-го и 3-го порядка на ОУ (Рис.2). В транзисторной реализации резисторы, задающие напряжение смещения на базе, уже участвуют в формировании необходимой АЧХ фильтра, поэтому значение Rб1 ll Rб2 должно равняться значению резистора R2 в ФВЧ 2-го порядка, либо R3 в ФВЧ 3-го порядка.

Рис.2

Номиналы элементов рассчитываются исходя из следующих формул:
R1=К_R1/(2π*F*C) R2=К_R2/(2π*F*C) R3=К_R3/(2π*F*C) R_rб1llR_rб2=R2 для фильтров 2-го порядка, либо R_rб1llR_rб2=R3 для 3-го.
Для фильтров Баттерворта 2-го порядка К_R1=0,707, К_R2=1,414, а для фильтров Баттерворта 3-го порядка К_R1=0,717, К_R2=0,282, К_R3=4,950.
И опять же, изначально надо определиться с номиналом R1, исходя из принципов, описанных в предыдущих схемах.

ТАБЛИЦА ДЛЯ РАСЧЁТА АКТИВНЫХ ФВЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА

И наконец, мы подобрались к схеме полосового активного фильтра.
Здесь всё несколько сложнее, поскольку, при расчёте фильтра, помимо значения центральной частоты, нам не стоит забывать и про такие немаловажные вещи, как коэффициент передачи фильтра в полосе пропускания, да и собственно ширину самой полосы пропускания.

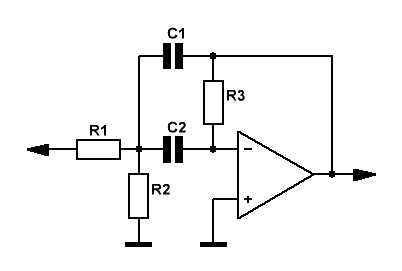Формулы, для расчёта элементов:
C1=C2=C
R1=Q/(2πF*Kп*C)
R2=Q/((2πF*C*(2Q²-Kп))
R3=2Q/(2πF*C)
Q=F/Bпр, где

Q-добротность фильтра,
Впр-полоса пропускания по уровню -3дБ,
F-центральная частота фильтра,
Кп-коэффициент передачи фильтра в полосе пропускания.
Рис.3

В фильтре, приведённом на рисунке, не стоит слишком усердствовать с высокими значениями добротности и коэффициента передачи. Как показывает практика, и тот и другой параметр следует ограничить сверху на уровне 5-6 единиц.

Как всегда, начинаем с выбора номинала резистора R1, который как минимум в 10 раз должен быть выше выходного импеданса предыдущего каскада.

РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНОГО ПЛОСОВОГО ФИЛЬТРА 2-го ПОРЯДКА

ВНИМАНИЕ!!! Для правильной работы этого фильтра должно соблюдаться условие К<2*Q². При несоблюдении этого условия, значение R2 в таблице примет отрицательное значение.

А что делать, если полученные значения элементов не попадают в стандартную сетку?
Не беда, нарисуем ещё одну таблицу, но до этого надо поиграться коэффициентом передачи фильтра в небольших пределах (например, сделать не 1,5, а 1,45, или 1,55) до достижения значения R3 величины, попадающей в сетку. Номинал R1 мы уже выбрали, исходя из соображений приемлемого входного импеданса.

Предположим, нам надо рассчитать фильтры для 10-полосного эквалайзера.
Фильтры у нас получаются октавные, стандартное значение добротности для них Q=1,41.
R1 выберем номиналом 30кОм, Кпер = 1,5. Произведём расчёт для частоты 1000 Гц.
Подставив эти цифры в верхнюю таблицу, получаем С=4987пФ, R2=18,173кОм, R3=90кОм.
Пошебуршав туда-сюда Кпер, понимаем, что для получения стандартного значения R3=91кОм, коэффициент передачи фильтра должен быть равен 1,517, что для нашего случая вообще не принципиально, тем более, что это значение Кпер будет сопровождать все фильтры, независимо от частоты.
Итак, подставляем в нижнюю таблицу R1=30кОм, R3=91кОм, R2=18кОм, стандартное значение ёмкости С=5100пФ и естественным образом видим, что значение резонансной частоты у нас съехало до 975Гц.
Но у нас было с собой, а именно замечательное сопротивление R2, которое никак не влияет на Кпер, и весьма скромно – на добротность.
Покрутив номинал этого резистора, получаем – 16,7кОм, центральную частоту – 999Гц и добротность – 1.46. Всё, расчёт фильтра – завершён.

ЕЩЁ ТАБЛИЦА ДЛЯ АКТИВНОГО ПОЛОСОВОГО ФИЛЬТРА

Для желающих рассчитать параметры и элементы многополосных графических эквалайзеров следует посетить страницу ссылка на страницу , а на следующей странице мы рассмотрим универсальный перестраиваемый активный фильтр с регулировкой частоты и добротности.